Обратные тригонометрические функции

1.

Обратные
тригонометрические
функции,
их свойства и графики.

2.

Определения обратных тригонометрических функций
Обратные тригонометрические функции -
(круговые функции, аркфункции) математические
функции, являющиеся обратными к тригонометрическим
функциям.
Арксинус ( y = arcsin x )
Арккосинус ( y = arccos x )
Арктангенс ( y = arctg x )
Арккотангенс ( y = arcctg x )

3.

Поскольку тригонометрические функции периодичны, то
обратные к ним функции не однозначны.
Так, уравнение y = sin x, при заданном
, имеет
бесконечно много корней. Действительно, в силу
периодичности sin, если x такой корень, то и x +
2πn (где n целое) тоже будет корнем уравнения.
Таким образом, обратные тригонометрические функции
многозначны. Чтобы с ними было проще работать, вводят
понятие их главных значений. Например, если для синуса
y = sin x,
если ограничить аргумент x интервалом
, то на этом
интервале функция y = sin x монотонно возрастает. Поэтому
она имеет однозначную обратную функцию, которую называют
арксинусом: x = arcsin y.

4.

Функция arcsin

5.

Свойства функции arcsin

6.

Получение функции arcsin

7.

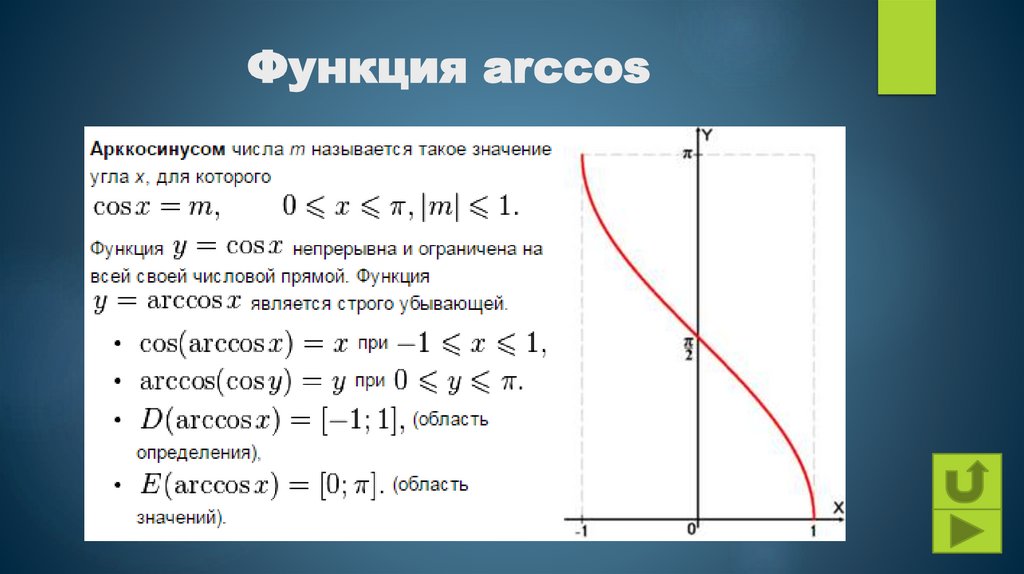
Функция arccos

8.

Свойства функции arccos

9.

Получение функции arccos

10.

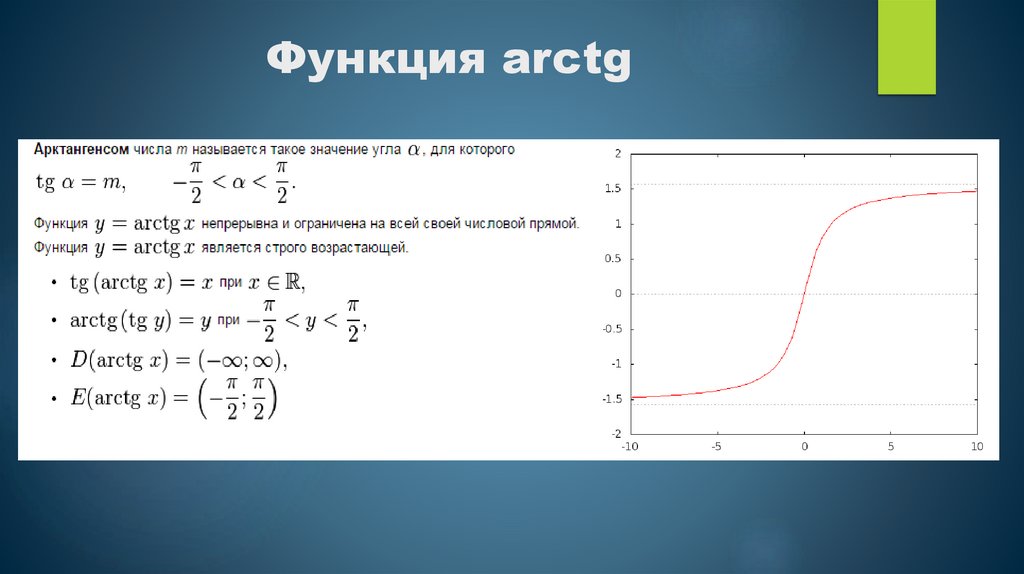
Функция arctg

11.

Свойства функции arctg

12.

Получение функции arctg

13.

Функция arcctg

14.

Свойства функции arcctg

15.

Получение функции arcctg

16.

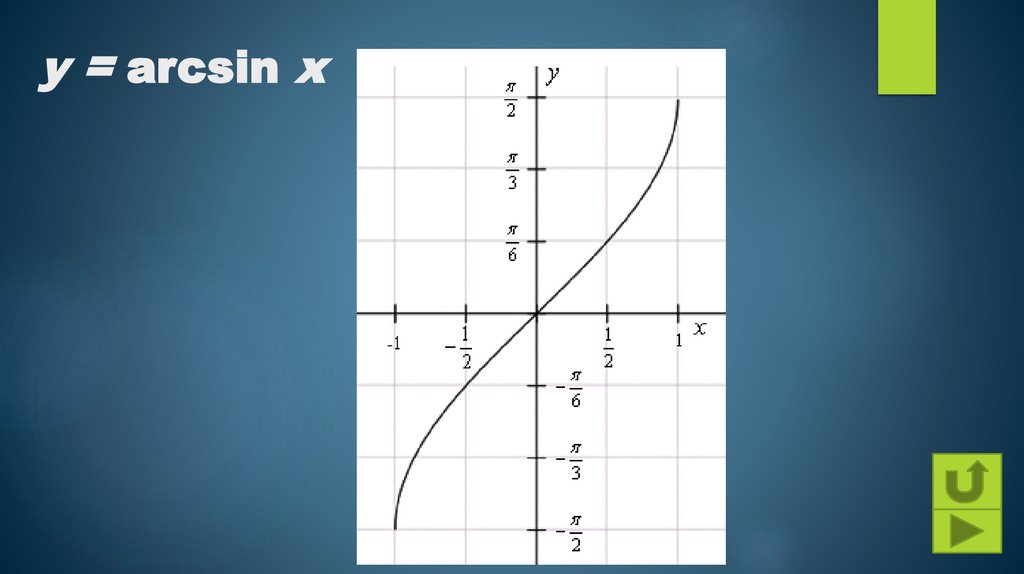
y = arcsin x

17.

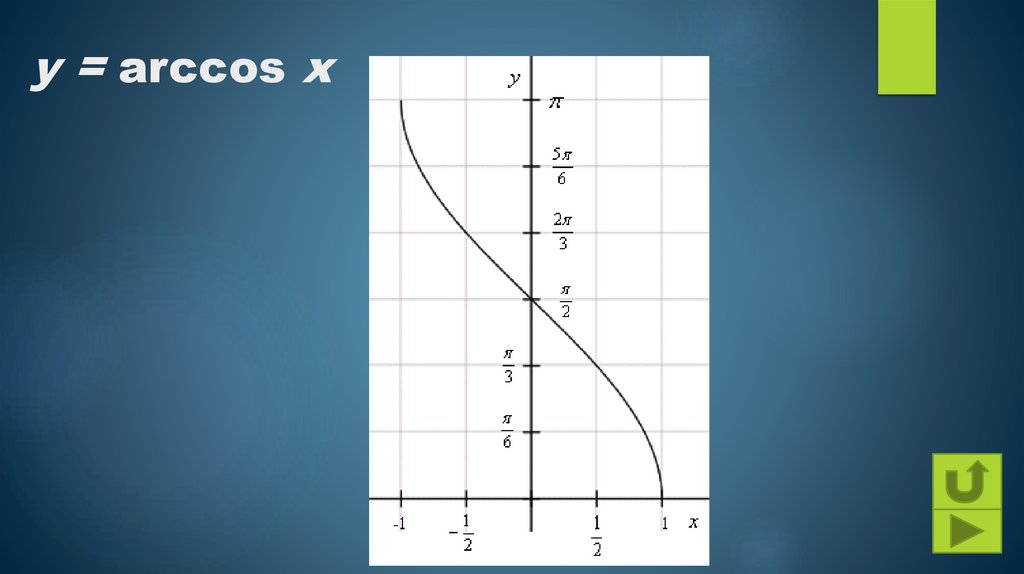
y = arccos x

18.

y = arctg x

19.

y = arcctg x

20.

Основные формулы
arcsin(sin x) = x
sin(arcsin x) = x
arccos(cos x) = x
cos(arccos x) = x
при
arctg(tg x) = x
tg(arctg x) = x
arcctg(ctg x) = x
ctg(arcctg x) = x
при
при
при

21.

Формулы, связывающие обратные
тригонометрические функции