Похожие презентации:
Геометрическая вероятность. Случайный выбор точки из фигуры на плоскости, из отрезка, из дуги окружности
1.
Геометрическая вероятность.Случайный выбор точки из фигуры на
плоскости, из отрезка, из дуги
окружности
2.
Пример:Предположим, что мы с закрытыми глазами на карте
мира выбрали какую-то точку.
Какова вероятность, что выбранная нами точка
находится на территории Российского государства?
Для ответа на поставленный вопрос необходимо знать,
какую часть от общей площади карты занимает
именно Россия.
Вероятность события «Выбранная точка находится
на территории России» прямо пропорциональна
площади всей карты и не зависит от её формы и
расположения.
3.
Правило вычисления геометрической вероятностиДопустим, из фигуры F выбрана случайная
точка. Вероятность события G «Выбранная
точка принадлежит фигуре G, находящейся
внутри фигуры F», равна:
где SG — площадь фигуры G;
SF — площадь фигуры F.
4.
Площадь фигуры F должна бытьбольше 0 (на 0 делить мы не
можем).
5.
Помимо того, что случайную точку мы можем выбратьна плоскости, мы можем её выбрать ещё на отрезке.
Такой выбор мы будем называть: выбор точки из
отрезка и дуги окружности.
Пример:
Имеем отрезок AB. На этом отрезке случайным образом
ставится точка C.
Определи вероятность того, что точка C ближе к B, чем к A.
Решение.
Предположим, что точка O является серединой отрезка AB.
Описанное событие возможно только в том случае, если C лежит
внутри отрезка OB.
Рассчитаем вероятность этого события:
6.
Геометрическая вероятностьограничена значениями 0 и 1.
- 0 означает, что интересующее
нас событие ни в коем случае не
произойдёт;
- 1 означает, что событие, о котором
идёт речь, произойдёт 100 %.
Мы уже знаем, что случайную точку можно выбрать на
плоскости, на отрезке. Но точно так же случайную точку
можно выбрать и на дуге окружности.
7.
Пример:На окружности отмечены две точки M и K. Случайным образом
на этой же окружности выбрана точка C. Найди вероятность
того, что отрезок KC пересекает диаметр окружности
(проходящий через точку M).
Решение
Допустим, что длина заданной окружности равна l.
Событие, которое нас интересует — A «отрезок КС пересекает
диаметр MN» — может наступить, только если
точки K и C лежат на полуокружности MN.
Чтобы рассчитать длину полуокружности l, делим пополам
Рассчитаем вероятность события A:
8.
Задание 1Перед Машей лежит тетрадный лист в клетку.
Девочка подбрасывает монетку 27 по счёту раз.
Определи вероятность того, что монетка падает
на тетрадный лист и попадает сразу на 4 клетки.
Ответ:
-число исходов зависит от величины монетки и размеров
клеток на тетрадном листе;
-задача не связана с темой «Геометрическая
вероятность»;
-0,5;
-1
9.
Задание 2На отрезке ВС, который равен 34 см, случайным образом
отметили точку К. Определи, чему равна вероятность
того, что точка К попала на отрезок MN, который
равен 10 см.
(Ответ округли до сотых.)
10.
Задание 3Дан треугольник ABC, площадь которого равна 69 см2. В
треугольнике случайным образом поставили точку T.
Определи вероятность того, что данная точка
принадлежит треугольнику XYZ (находится внутри
треугольника ABC), площадь которого равна 43 см2.
(Ответ округли до сотых.)
11.
Задание 4Дан отрезок: [0;4].
Определи вероятность того, что точка,
поставленная на этом отрезке наугад, попадёт в
промежуток [1,1;3].
(Ответ округли до сотых.)
12.
Задание 5На производстве порвался канат, длина
которого составляет 41 м.
Определи вероятность того, что после обрыва
имеется канат длиной не менее 35 м.
(Ответ округли до сотых.)
13.
Задание 6Дан прямоугольник со сторонами 8 см на 21 см. На
прямоугольнике выбирается одна случайная точка K.
Какова вероятность того, что точка K попала в верхний
правый квадрат со стороной 3 см?
(Ответ округли до сотых.)
14.
Задание 7На рисунке изображена
вертушка. Вертушку
сильно раскручивают
и ждут полной её
остановки. Определи
вероятность того, что
стрелка остановится
на красном секторе
вертушки.
Площадь двух красных
секторов составляет
16,5 см2.
(Все вычисления округляй до сотых.)
15.
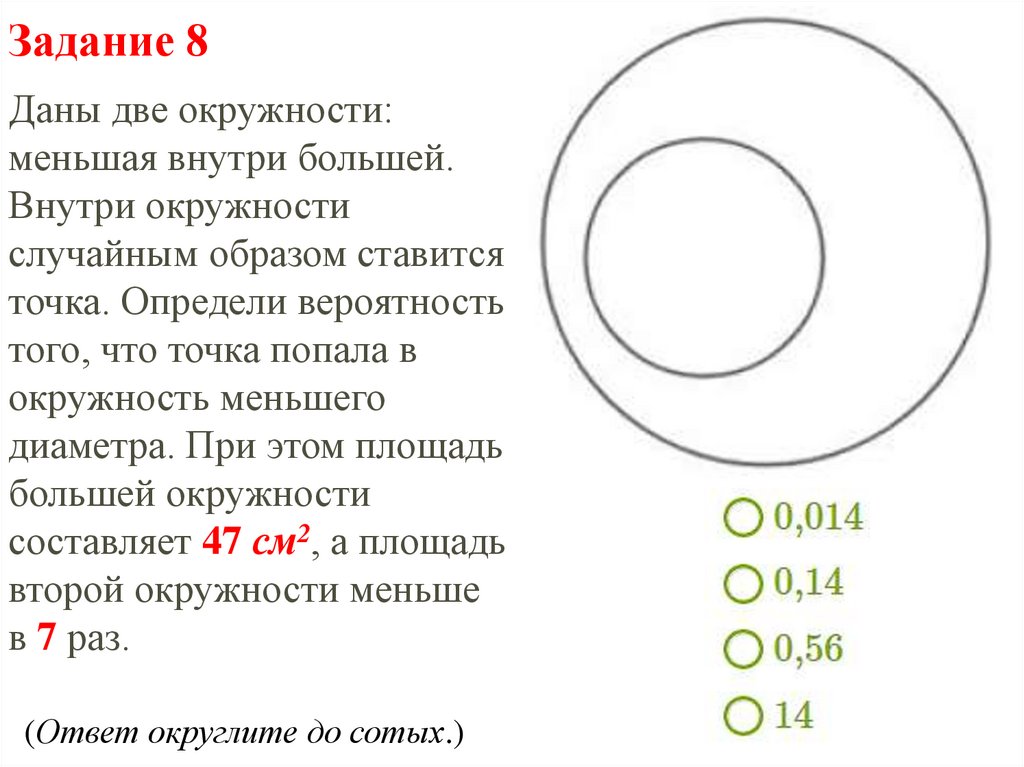
Задание 8Даны две окружности:
меньшая внутри большей.
Внутри окружности
случайным образом ставится
точка. Определи вероятность
того, что точка попала в
окружность меньшего
диаметра. При этом площадь
большей окружности
составляет 47 см2, а площадь
второй окружности меньше
в 7 раз.
(Ответ округлите до сотых.)
16.
Задание 9Дан прямоугольник, длина которого
составляет 15 см, а ширина —
6 см. Внутри этого прямоугольника
изобразили круг с радиусом 2 см.
Определи вероятность того, что точка,
которую поставили случайным образом
на прямоугольнике, окажется внутри
этого круга.
(При вычислениях прими π≈3,14. Ответ
округли до сотых.)
17.
Домашнее заданиеЗадание 1
На отрезке ВС, который равен 24 см, случайным
образом отметили точку К. Определи, чему равна
вероятность того, что точка К попала на отрезок MN,
который равен 6 см.
(Ответ округли до сотых.)
18.
Домашнее заданиеЗадание 2
Дан треугольник ABC, площадь которого
равна 96 см2. В треугольнике случайным
образом поставили точку T. Определи
вероятность того, что данная точка
принадлежит треугольнику XYZ (находится
внутри треугольника ABC), площадь которого
равна 43 см2.
(Ответ округли до сотых.)
19.
Домашнее заданиеЗадание 3
Дан отрезок: [0;5]. Определи вероятность того,
что точка, поставленная на этом отрезке наугад,
попадёт в промежуток [0,3;3].
(Ответ округли до сотых.)


















 Математика
Математика








