Конус

1.

2.

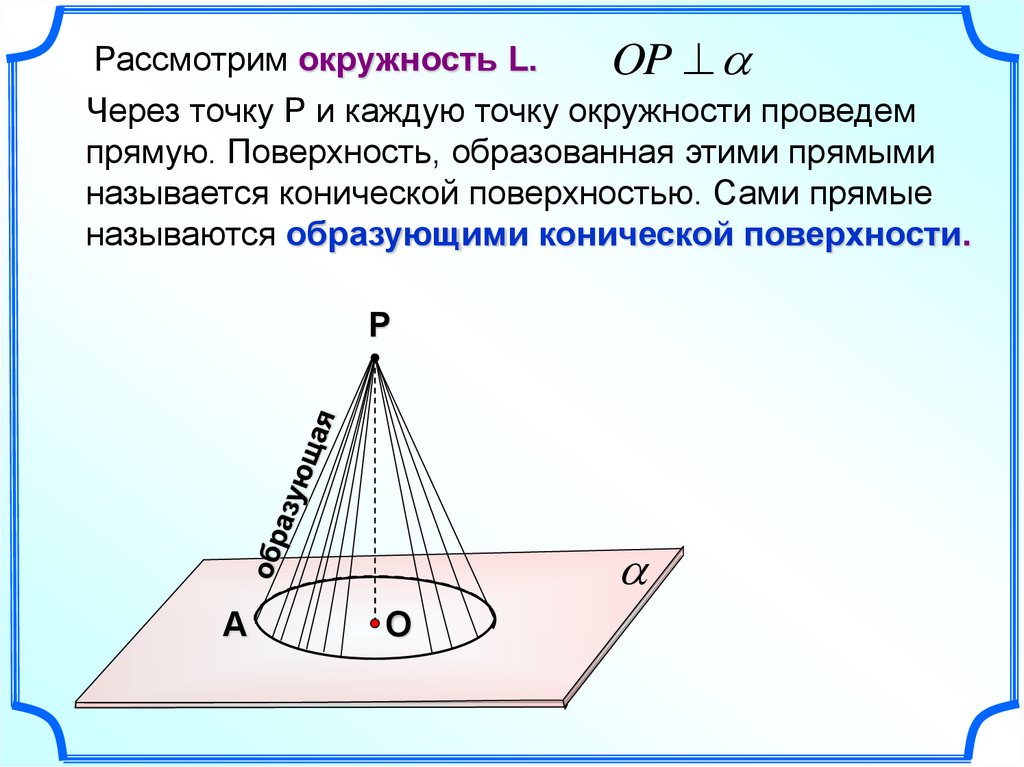
Рассмотрим окружность L.
OP
Через точку Р и каждую точку окружности проведем
прямую. Поверхность, образованная этими прямыми
называется конической поверхностью. Сами прямые
называются образующими конической поверхности.
P
А
O

3.

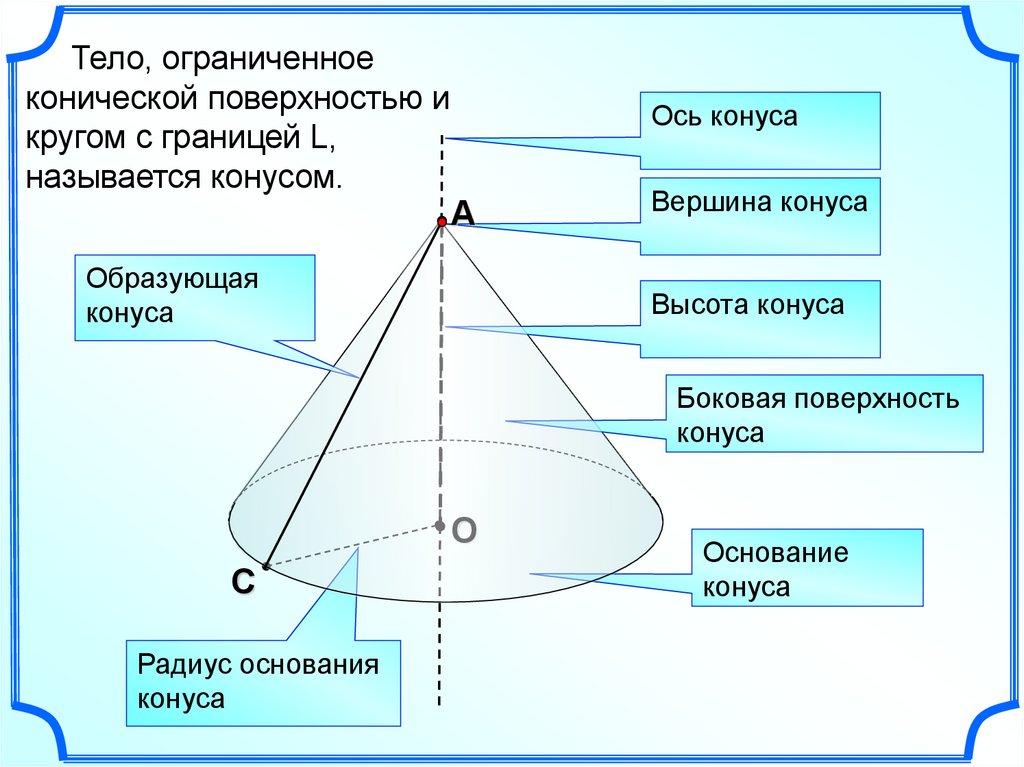
Тело, ограниченное
конической поверхностью и
кругом с границей L,
называется конусом.
Ось конуса
А
Образующая
конуса
Вершина конуса
Высота конуса
Боковая поверхность
конуса
O
С
Радиус основания
конуса
Основание
конуса

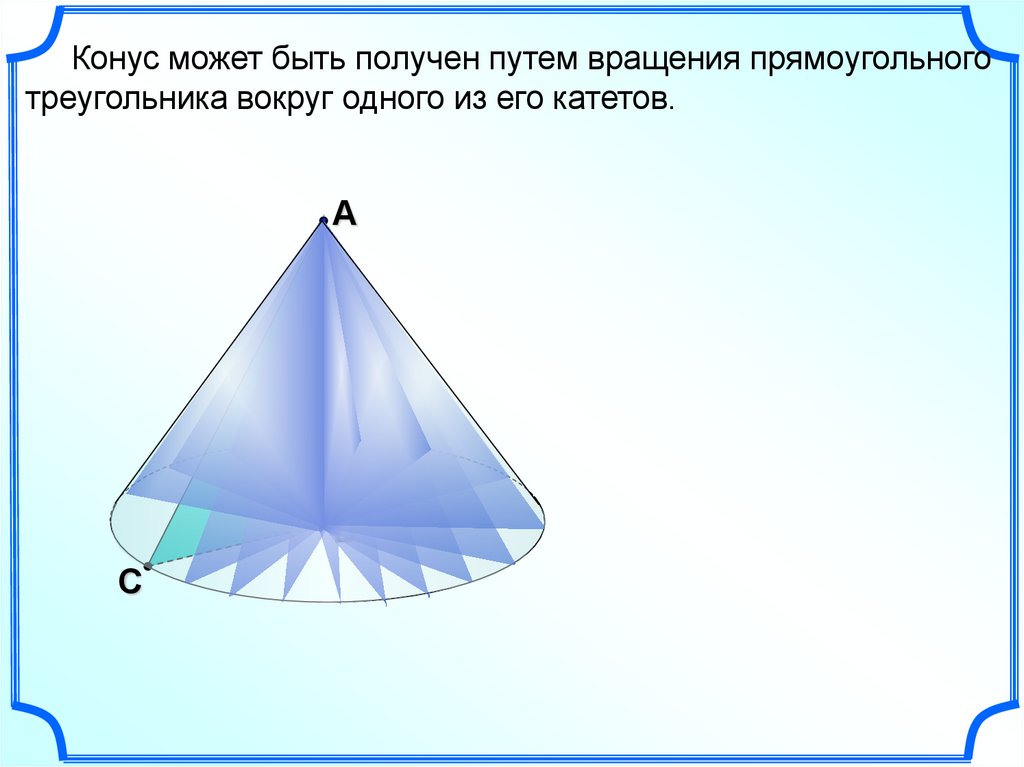
4.

Конус может быть получен путем вращения прямоугольного
треугольника вокруг одного из его катетов.
А
В
С

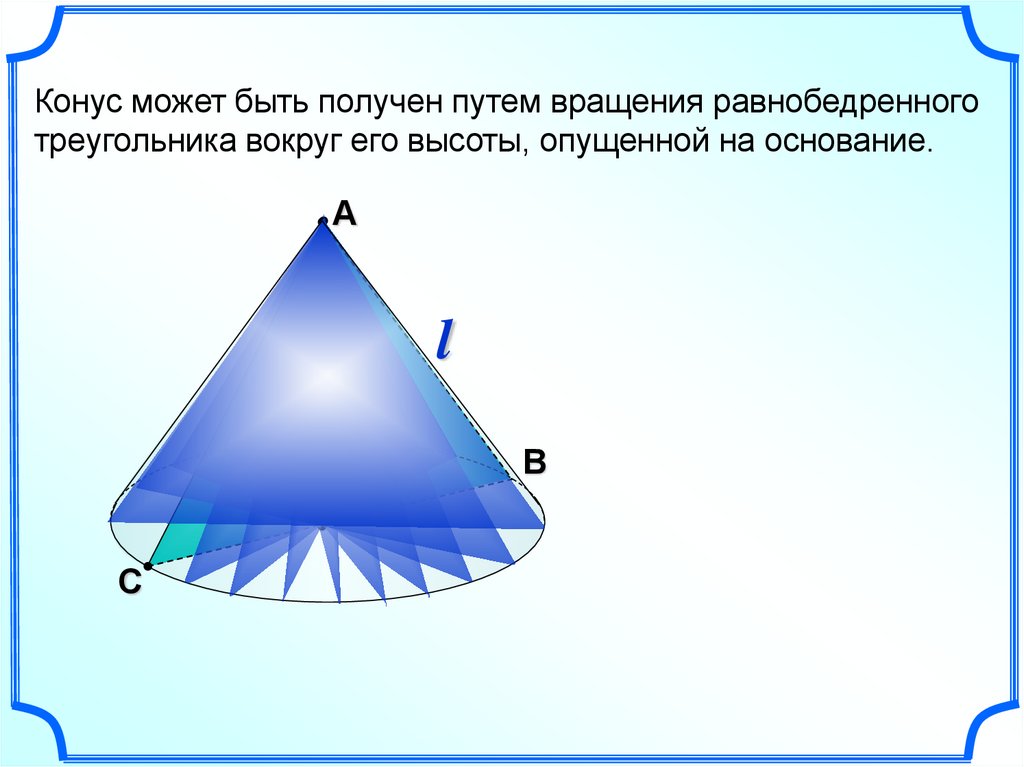
5.

Конус может быть получен путем вращения равнобедренного
треугольника вокруг его высоты, опущенной на основание.
А
l
В
С

6.

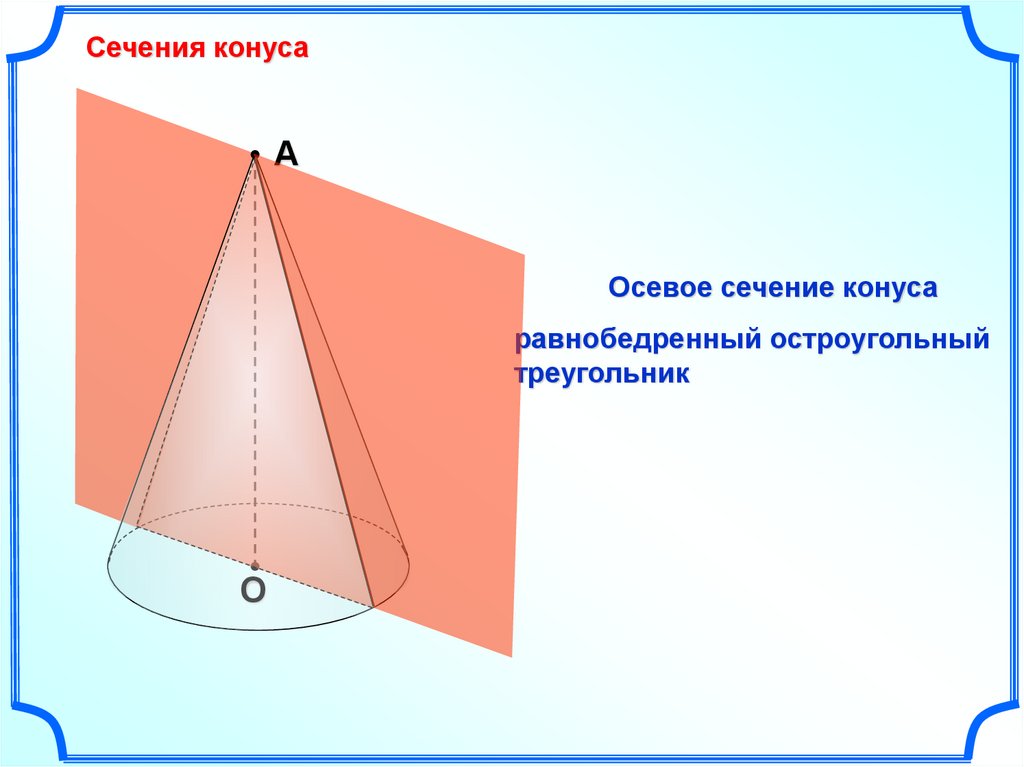
Сечения конуса
А
Осевое сечение конуса
равнобедренный остроугольный
треугольник
О

7.

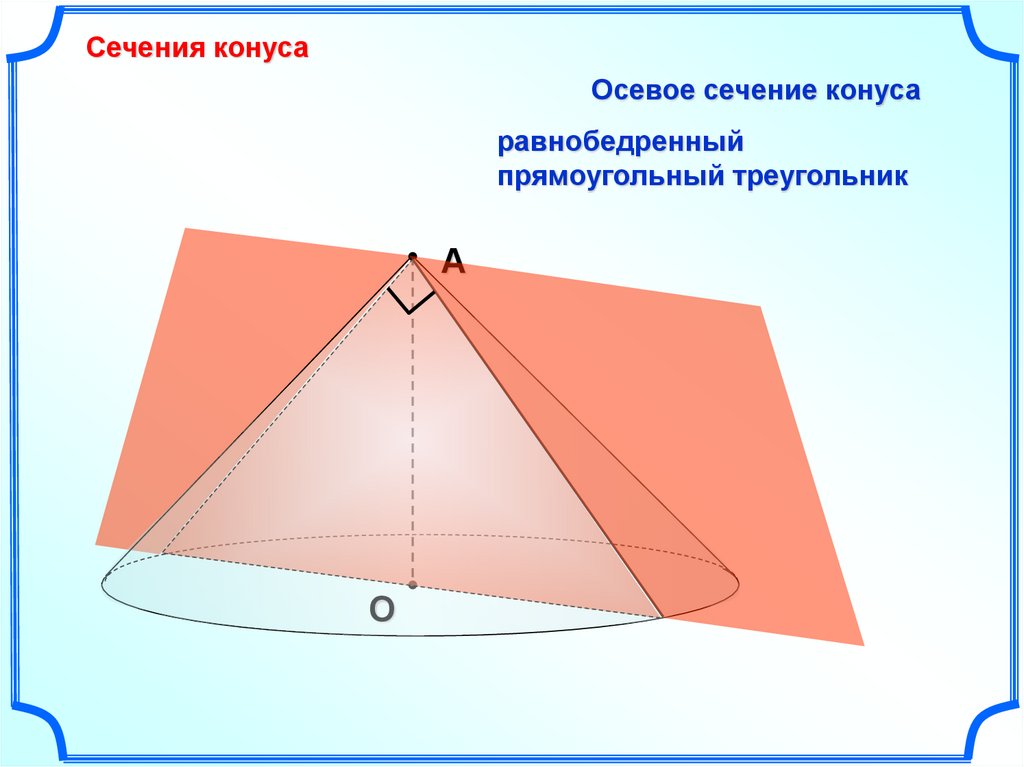
Сечения конуса
Осевое сечение конуса
равнобедренный
прямоугольный треугольник
А
О

8.

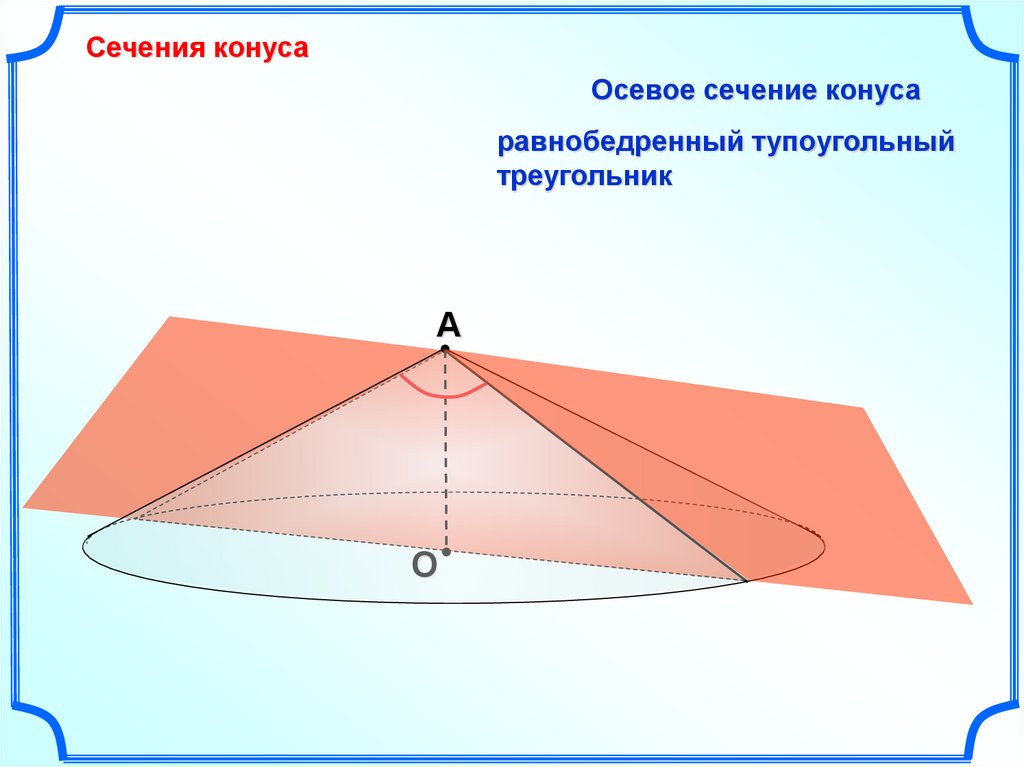
Сечения конуса
Осевое сечение конуса
равнобедренный тупоугольный
треугольник
А
О

9.

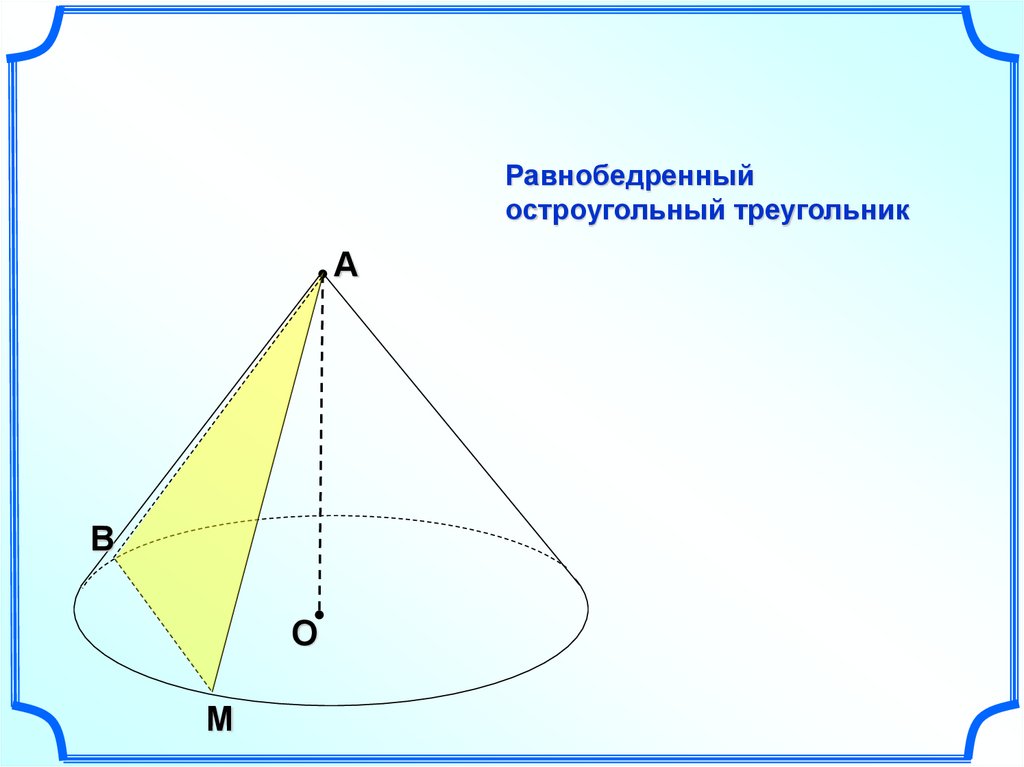
Равнобедренный
остроугольный треугольник
А
B
О
M

10.

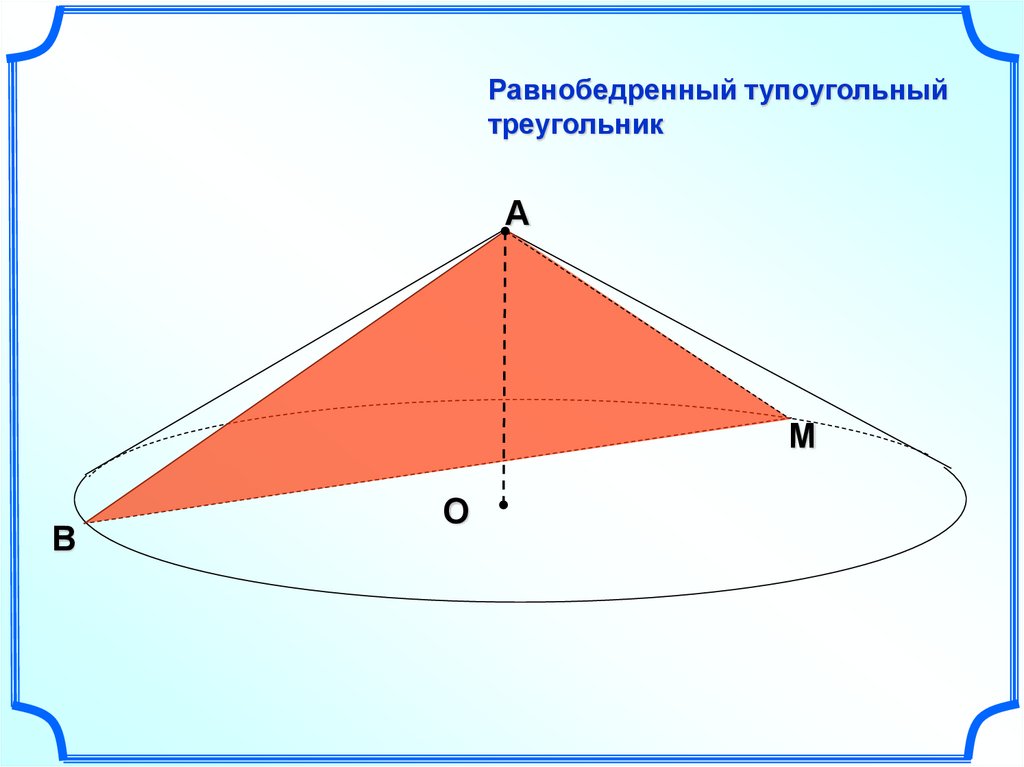
Равнобедренный тупоугольный
треугольник
А
M
B
О

11.

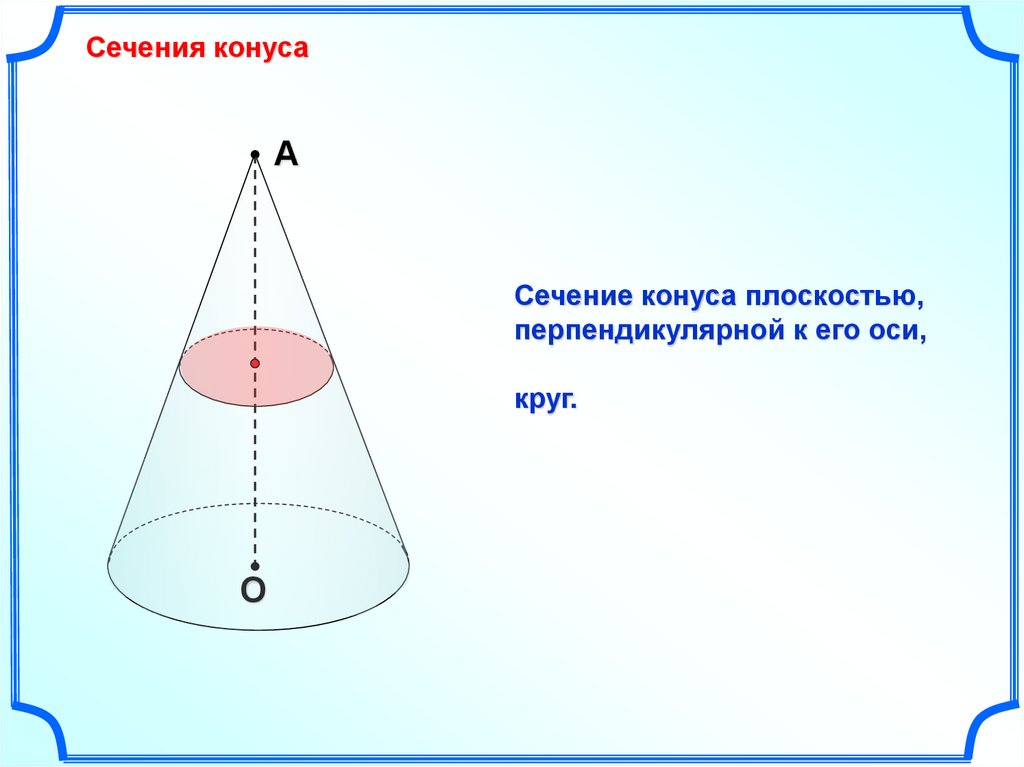
Сечения конуса
А
Сечение конуса плоскостью,
перпендикулярной к его оси,
круг.
О

12.

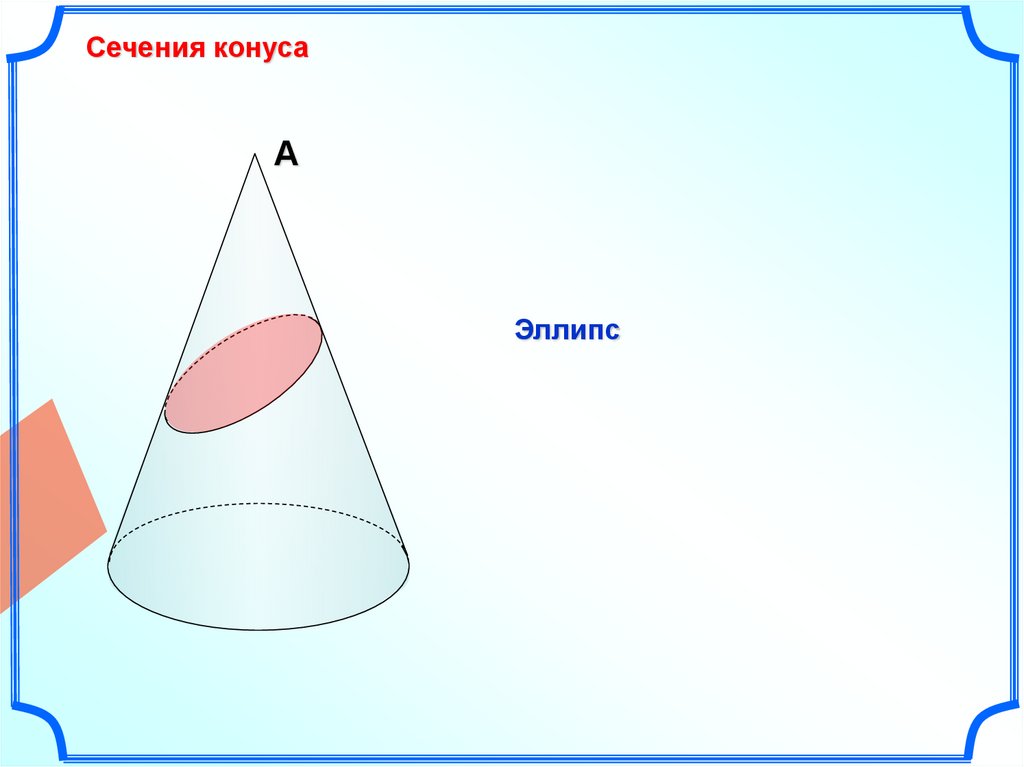
Сечения конуса
А
Эллипс

13.

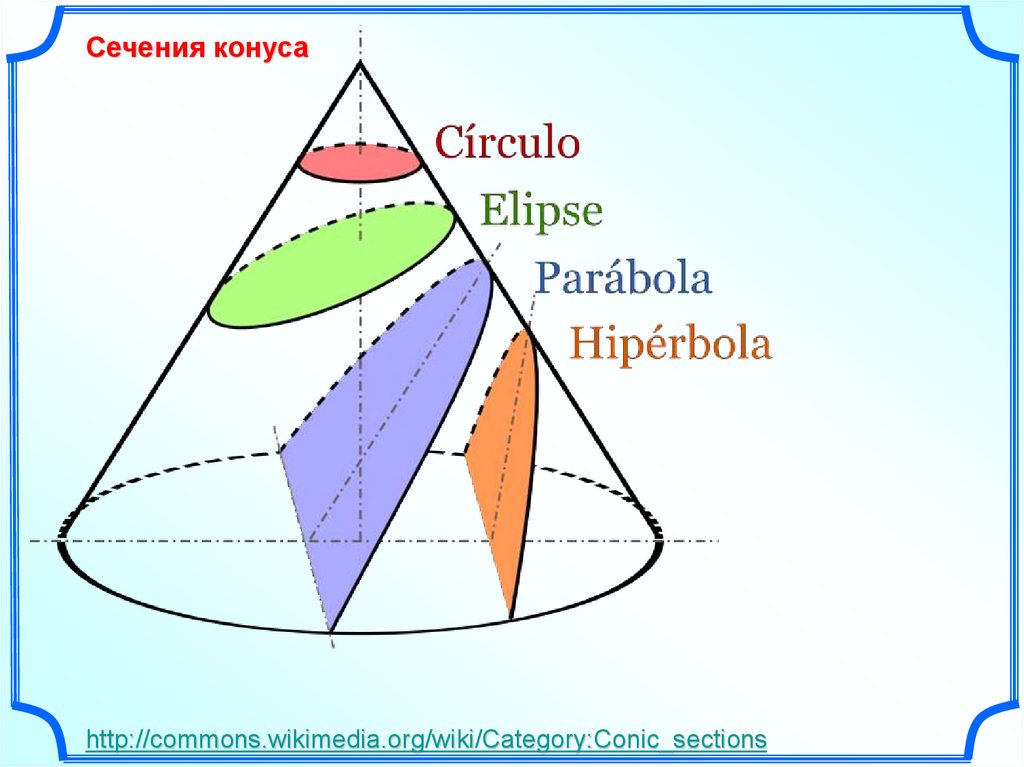
Сечения конуса
http://commons.wikimedia.org/wiki/Category:Conic_sections

14.

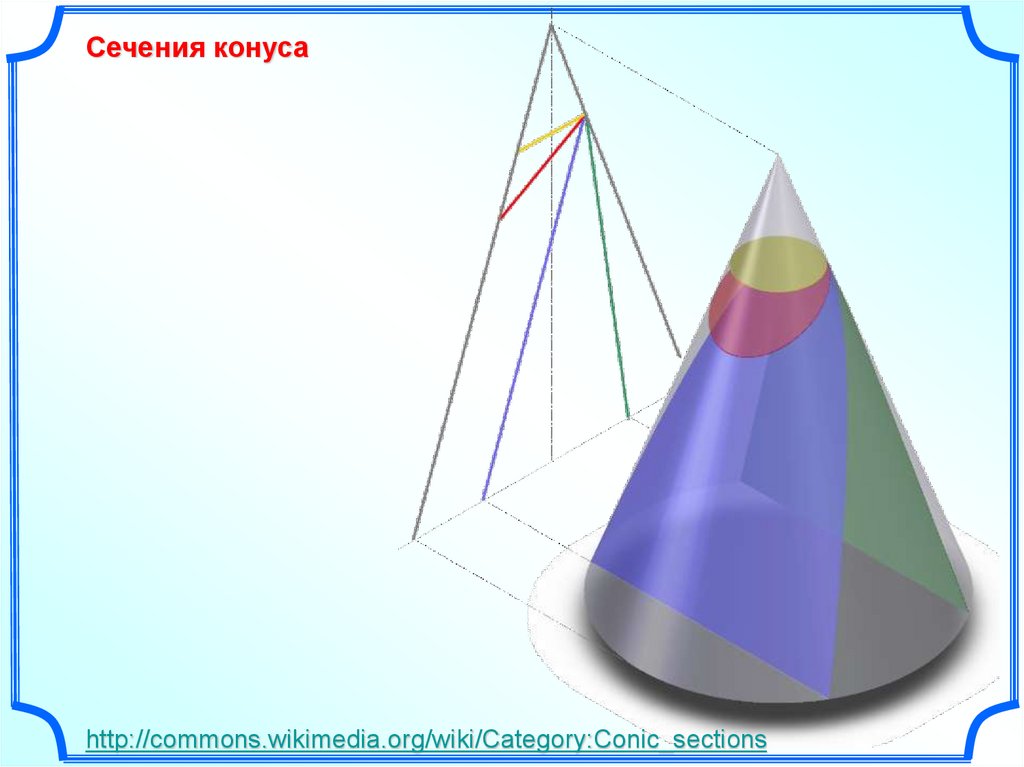
Сечения конуса
http://commons.wikimedia.org/wiki/Category:Conic_sections

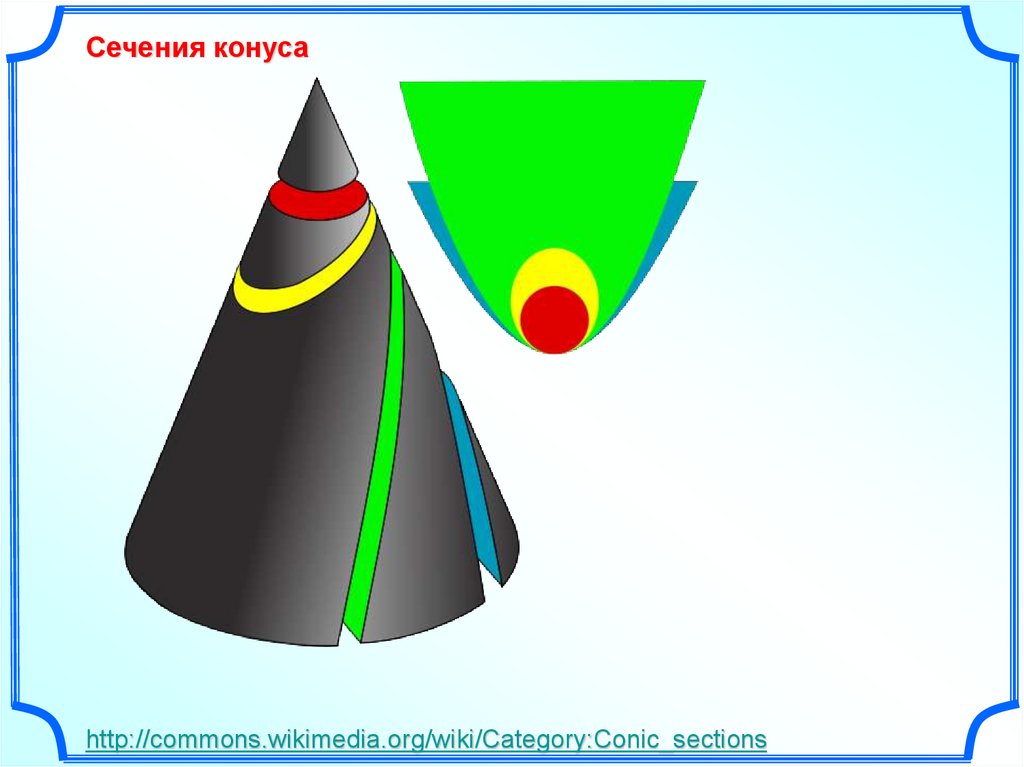
15.

Сечения конуса
http://commons.wikimedia.org/wiki/Category:Conic_sections

16.

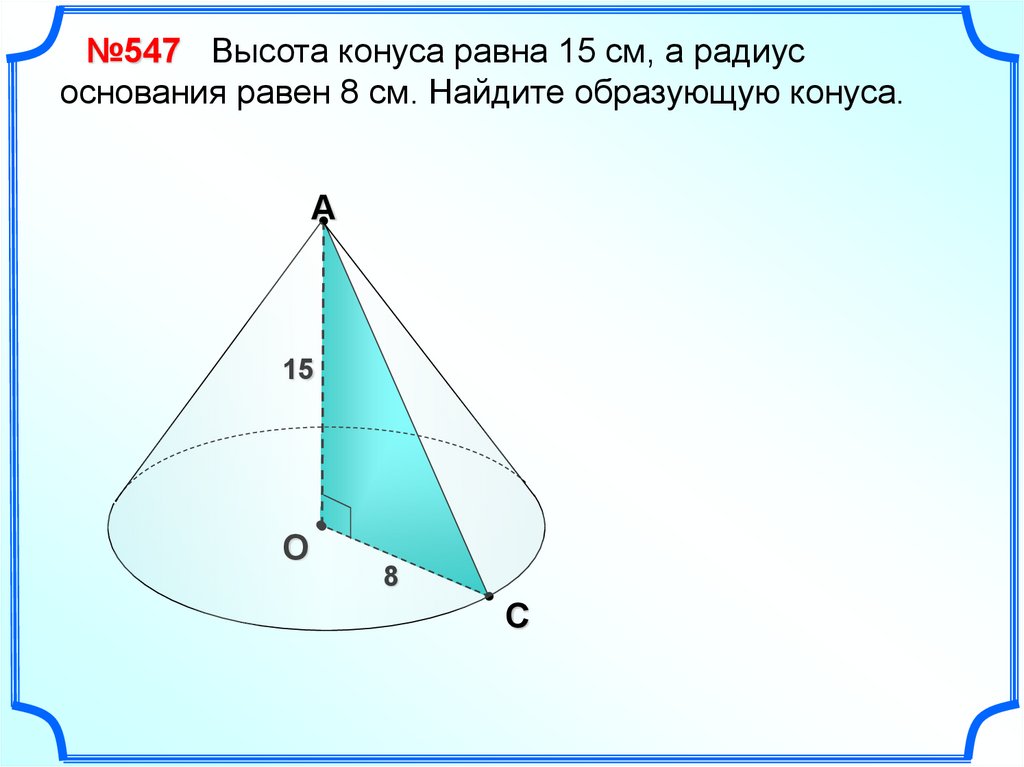
№547 Высота конуса равна 15 см, а радиус
основания равен 8 см. Найдите образующую конуса.
А
15
О
8
С

17.

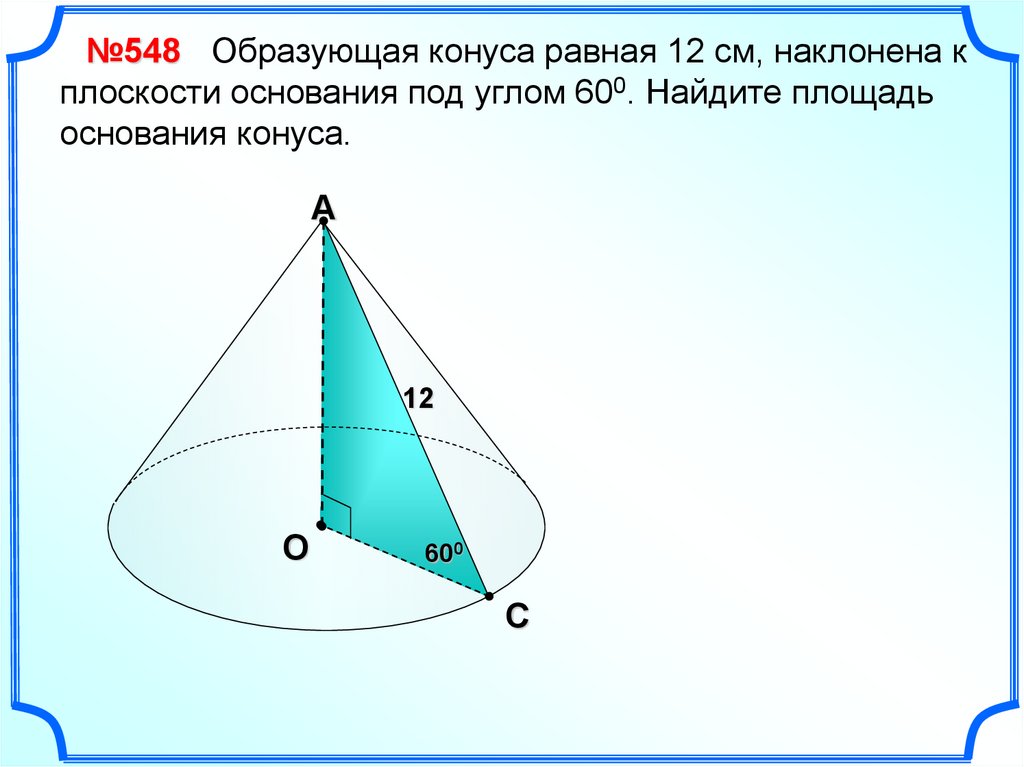
№548 Образующая конуса равная 12 см, наклонена к
плоскости основания под углом 600. Найдите площадь
основания конуса.
А
12
О
600
С

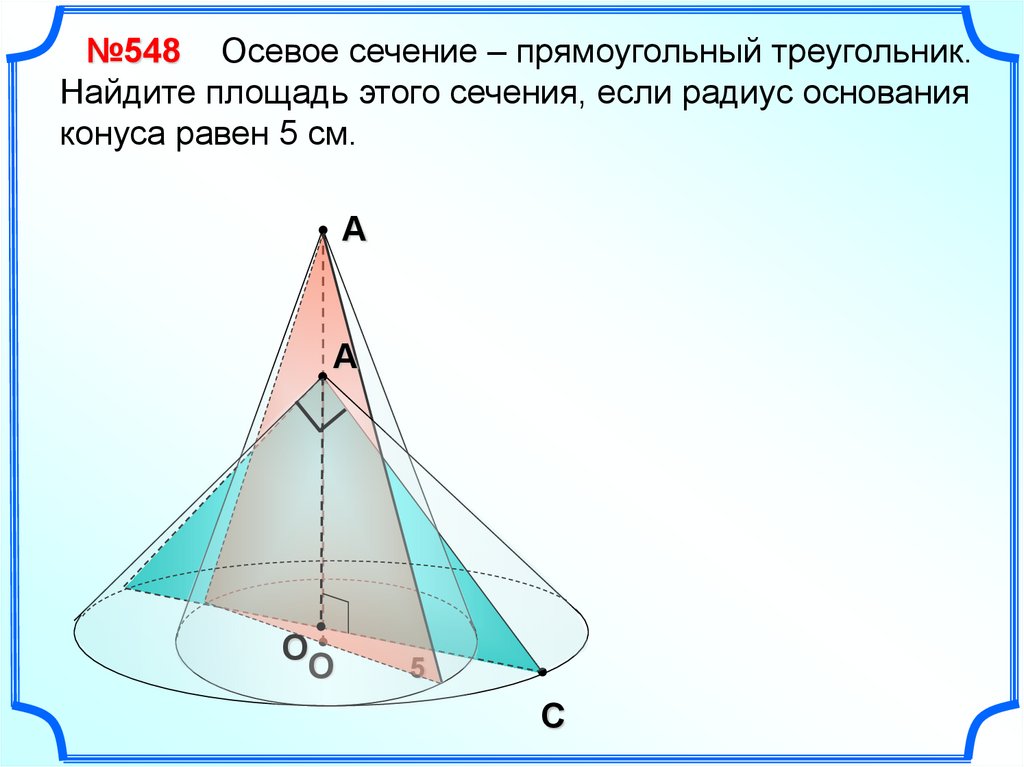
18.

№548 Осевое сечение – прямоугольный треугольник.
Найдите площадь этого сечения, если радиус основания
конуса равен 5 см.
А
А
О
О
5
С

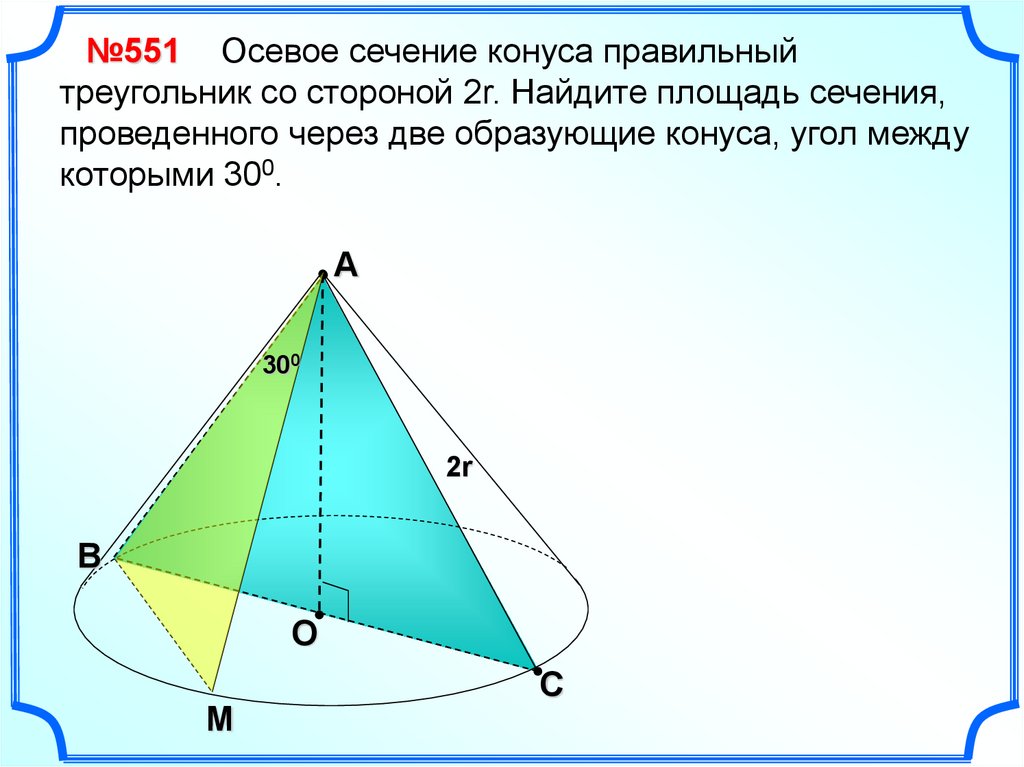
19.

№551 Осевое сечение конуса правильный
треугольник со стороной 2r. Найдите площадь сечения,
проведенного через две образующие конуса, угол между
которыми 300.
А
300
2r
B
О
С
M

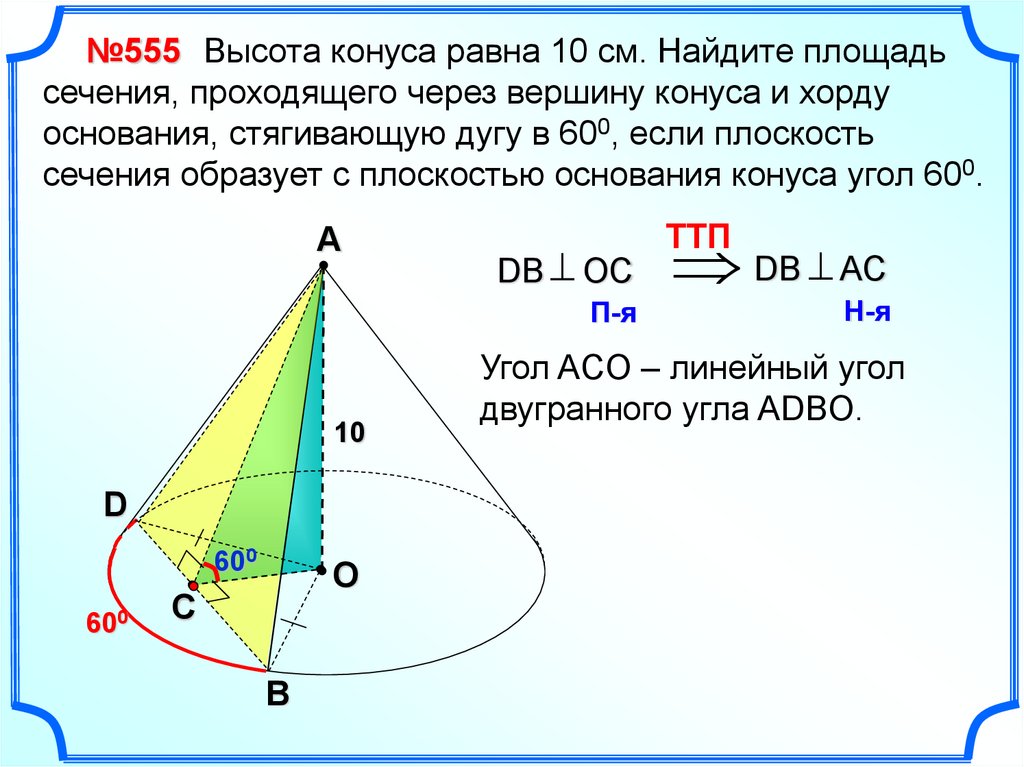
20.

№555 Высота конуса равна 10 см. Найдите площадь
сечения, проходящего через вершину конуса и хорду
основания, стягивающую дугу в 600, если плоскость
сечения образует с плоскостью основания конуса угол 600.
А
DB OC
П-я
10
D
600
600
О
С
B
DB AC
TTП
Н-я
Угол ACO – линейный угол
двугранного угла ADBO.

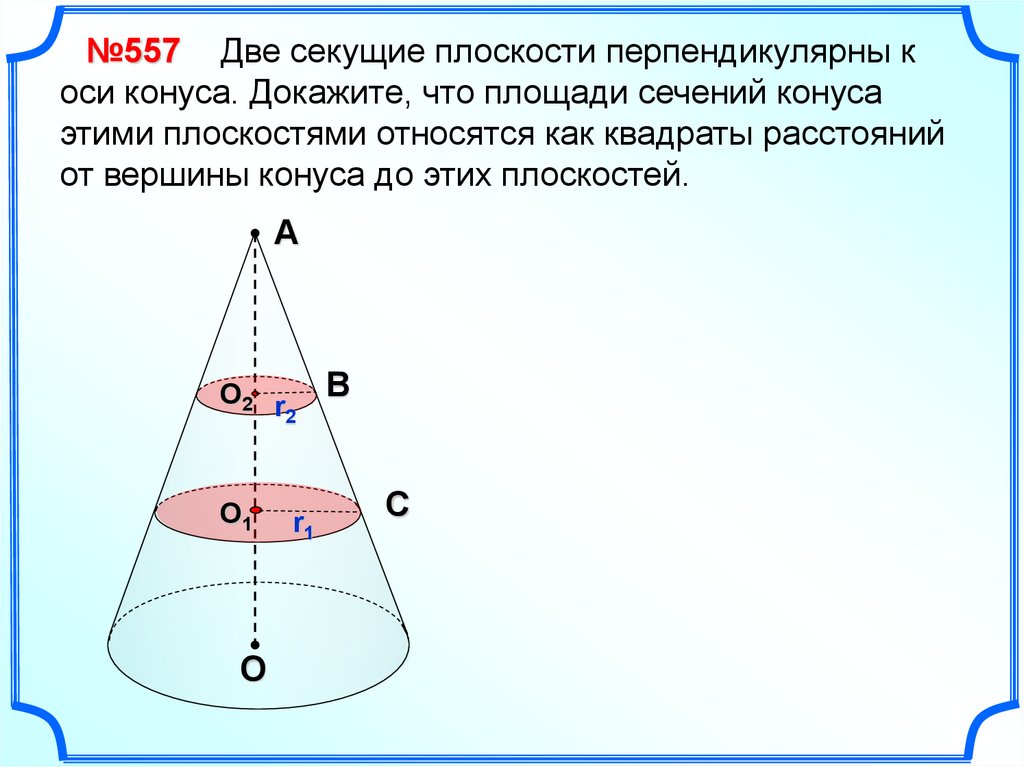
21.

№557 Две секущие плоскости перпендикулярны к
оси конуса. Докажите, что площади сечений конуса
этими плоскостями относятся как квадраты расстояний
от вершины конуса до этих плоскостей.
А
О2 r
2
О1
О
r1
B
C

22.

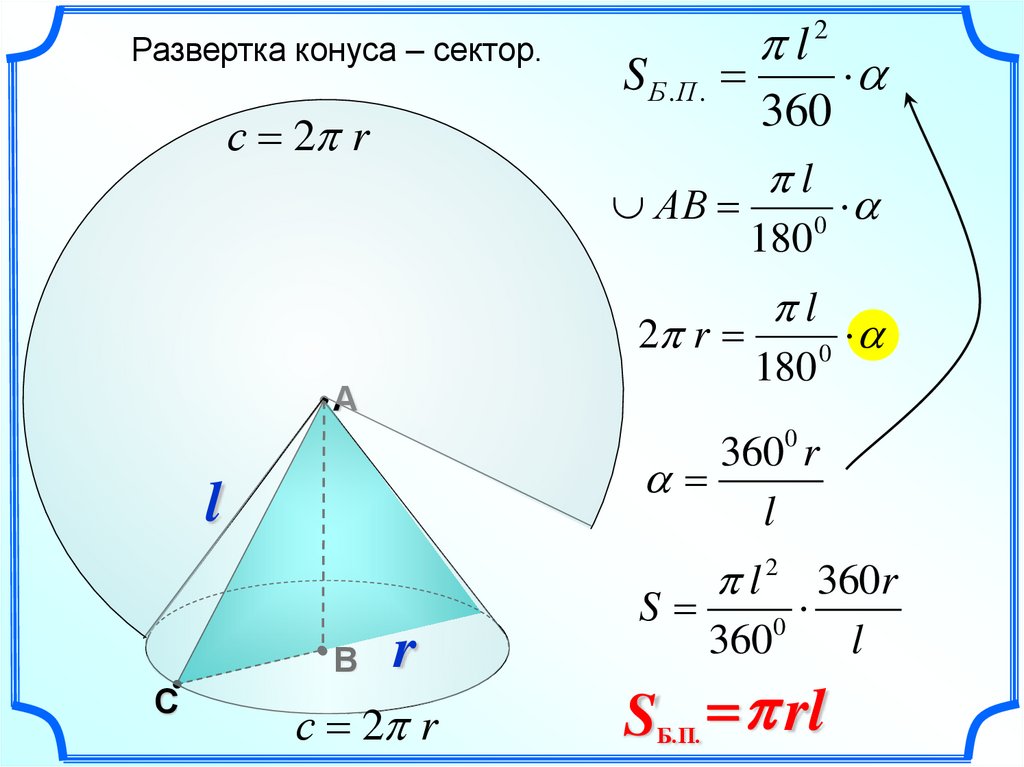
Развертка конуса – сектор.
с 2 r
S Б.П .
АВ
2 r
А
l2
360
l
180
l
180
0
3600 r
l
l
l
В
С
0
r
с 2 r
2
360r
S
0
360
l
S rl
Б.П.

23.

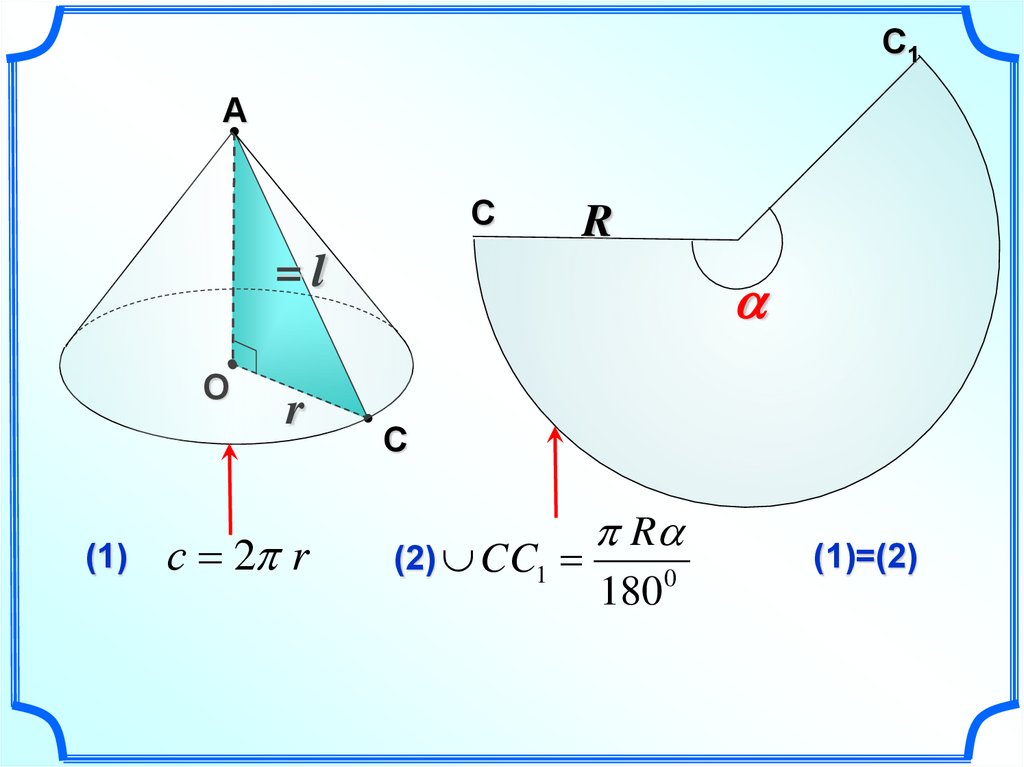
С1
А
С
R
=l
О
(1)
r
с 2 r
С
(2) CC1
R
180
0
(1)=(2)

24.

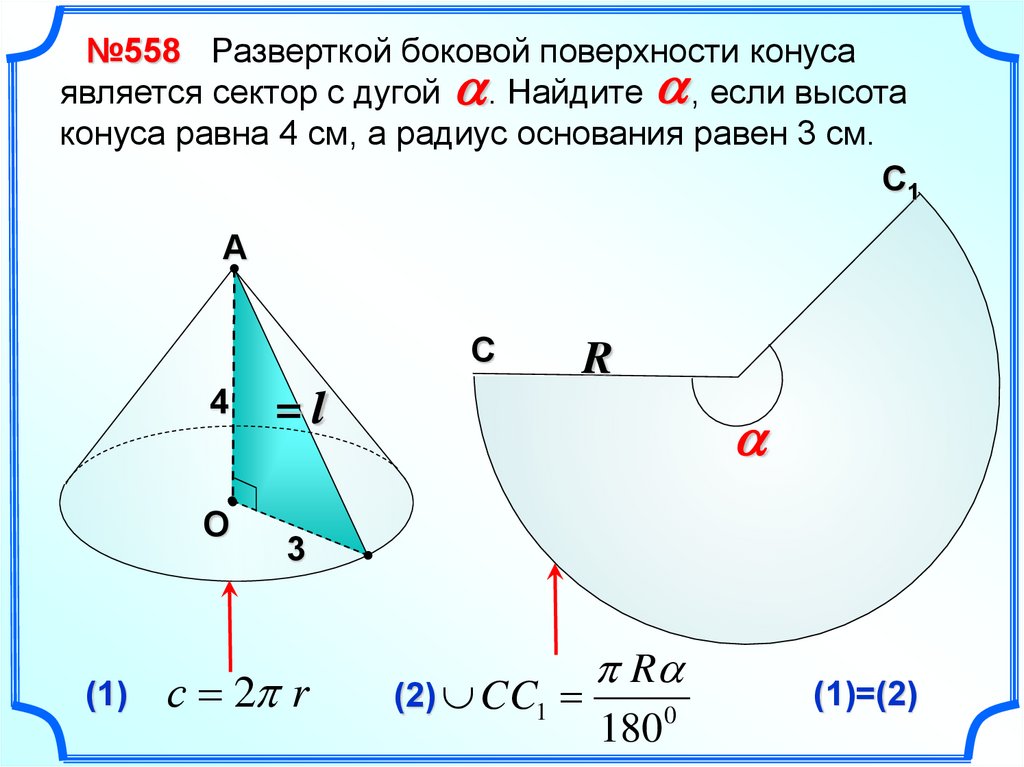
№558 Разверткой боковой поверхности конуса
является сектор с дугой . Найдите , если высота
конуса равна 4 см, а радиус основания равен 3 см.
С1
А
С
4
О
(1)
R
=l
3
с 2 r
(2) CC1
R
180
0
(1)=(2)

25.

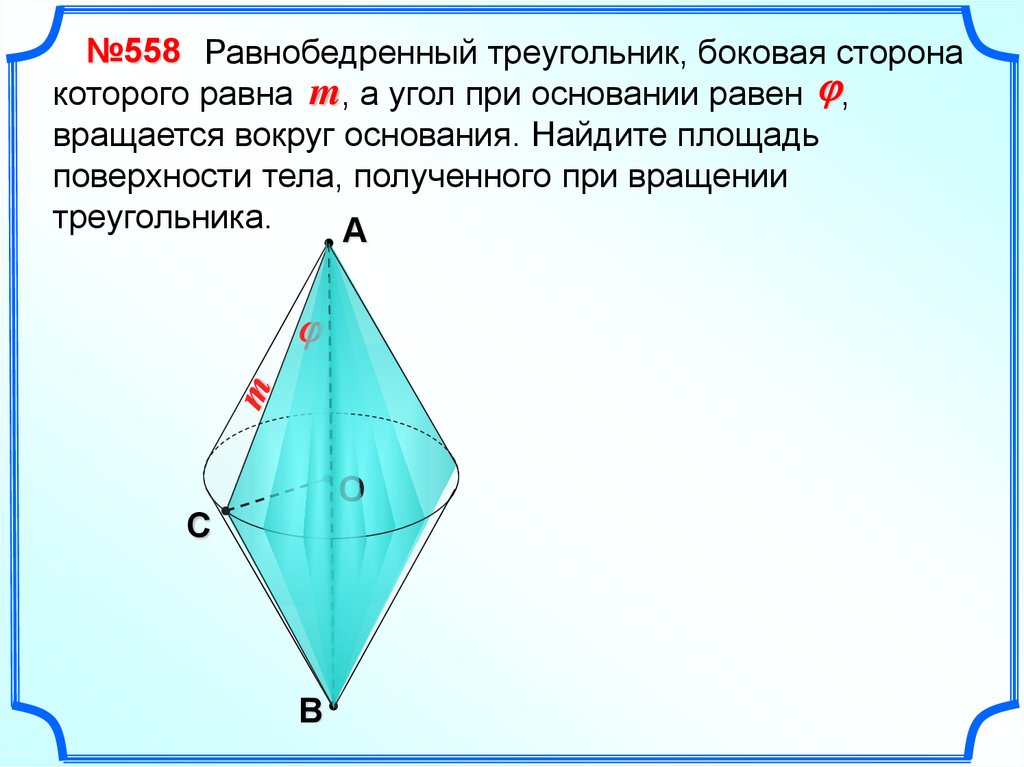
№558 Равнобедренный треугольник, боковая сторона
которого равна m, а угол при основании равен j,
вращается вокруг основания. Найдите площадь
поверхности тела, полученного при вращении
треугольника.
А
j
О
С
B

26.

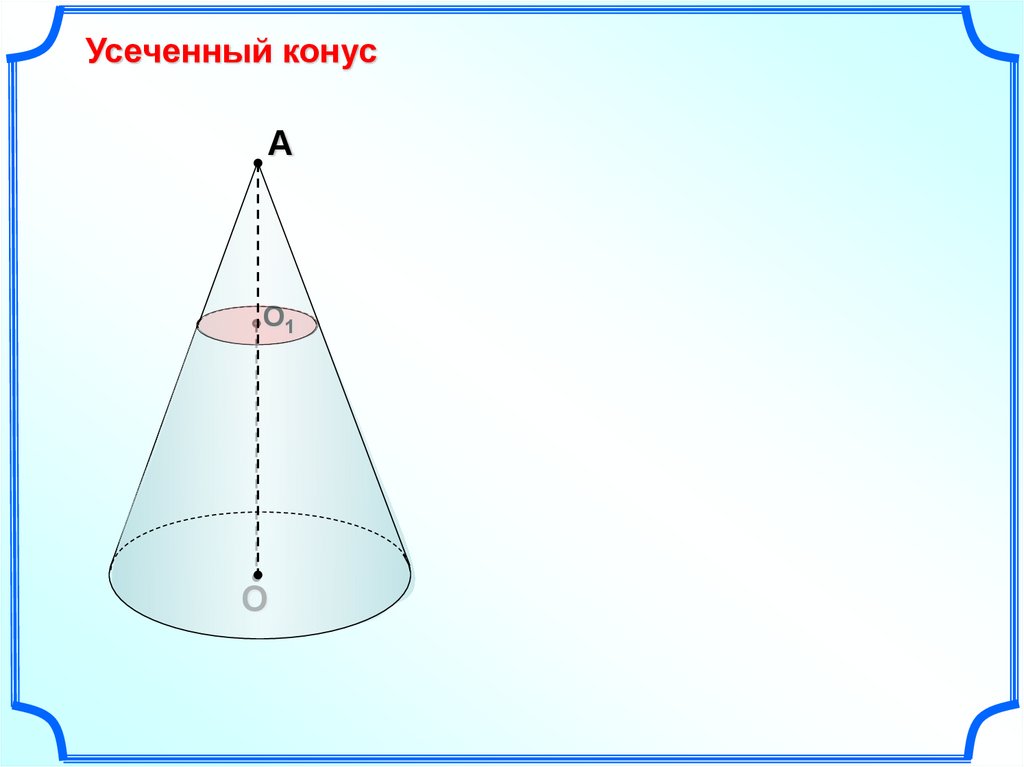
Усеченный конус
А
O1
О

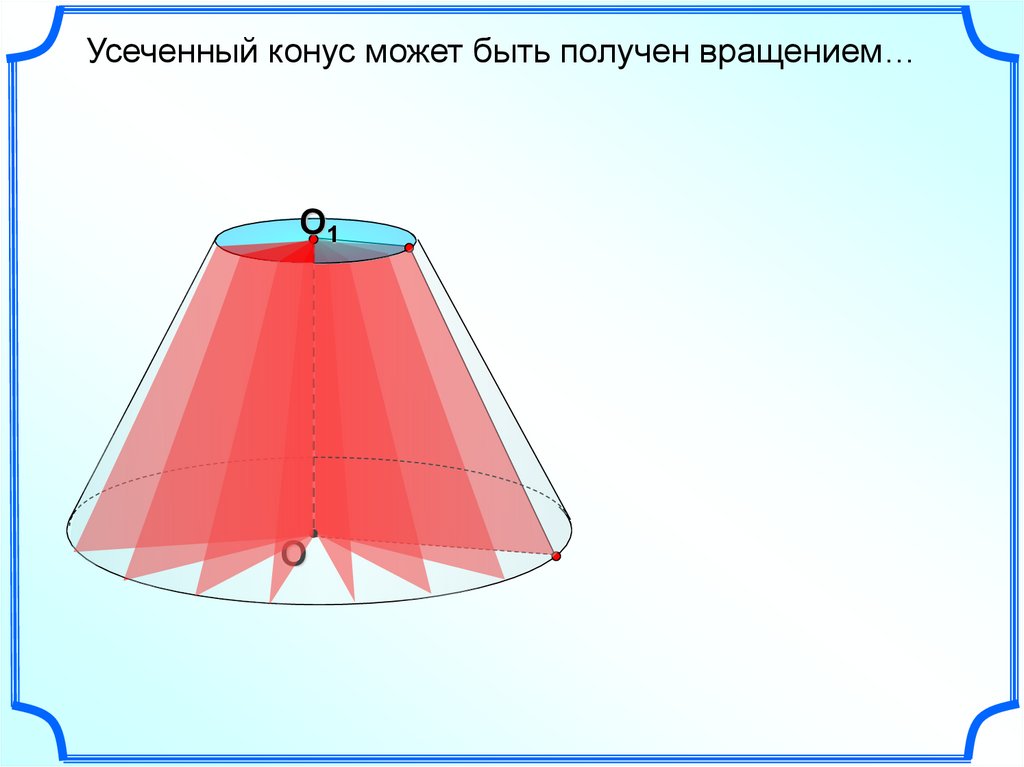
27.

Усеченный конус может быть получен вращением…
O1
О

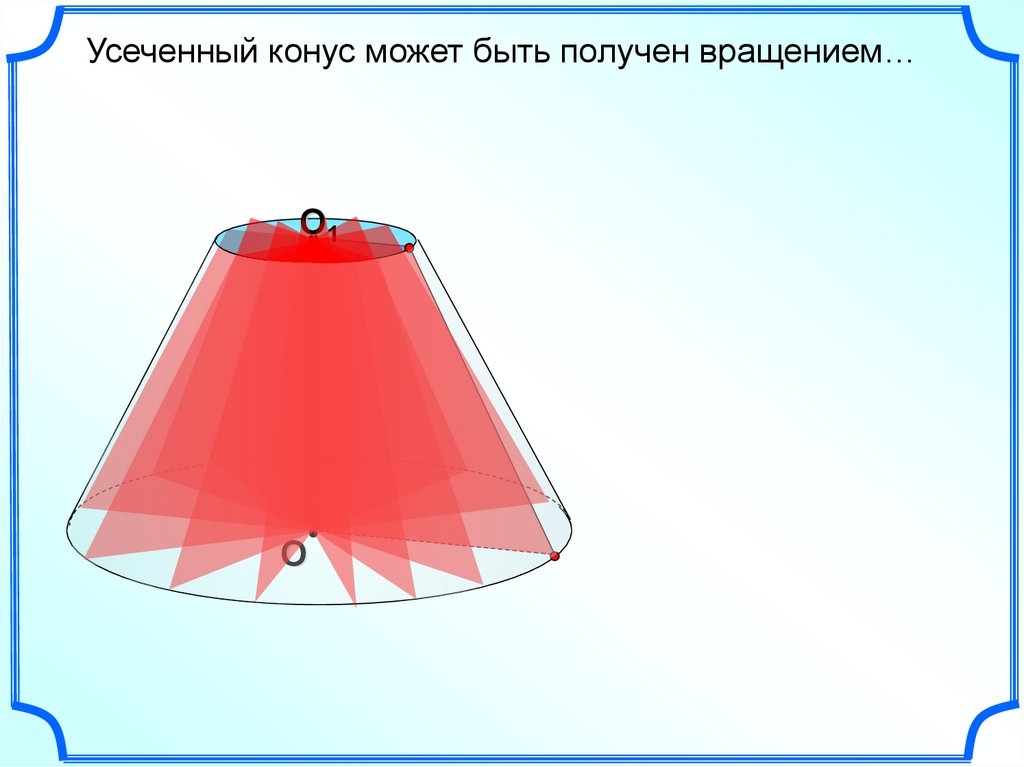
28.

Усеченный конус может быть получен вращением…
O1
О

29.

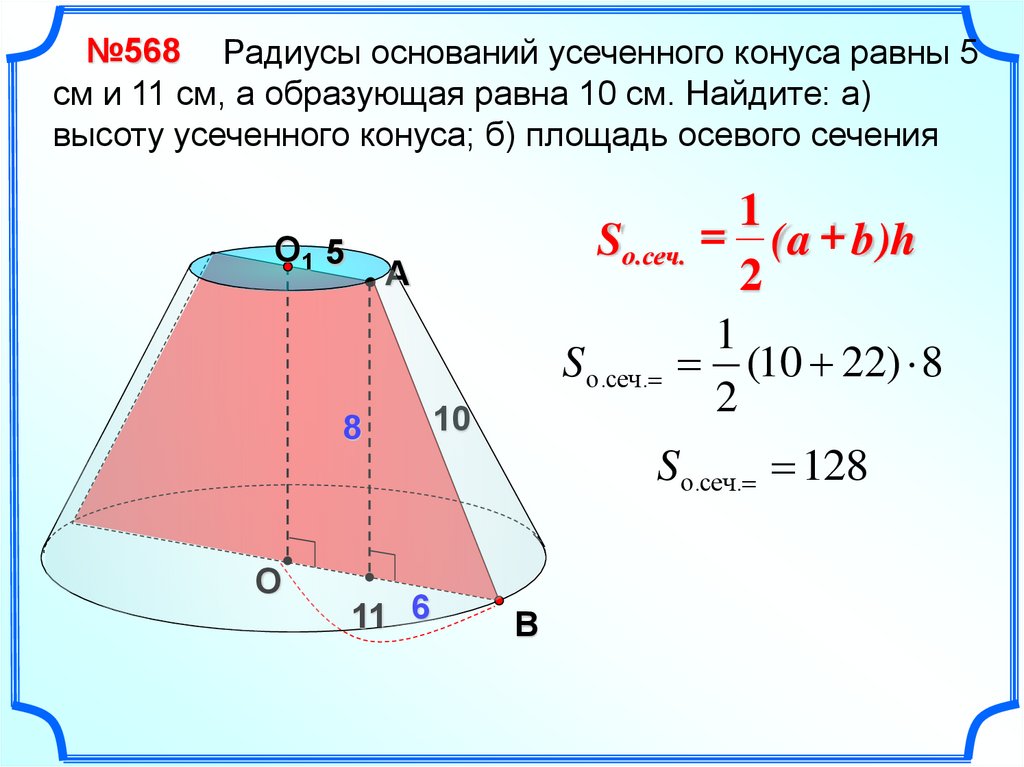
№568 Радиусы оснований усеченного конуса равны 5
см и 11 см, а образующая равна 10 см. Найдите: а)
высоту усеченного конуса; б) площадь осевого сечения
O1 5
A
8
О
1
Sо.сеч. = ( a + b)h
2
1
S о.сеч. (10 22) 8
2
Sо.сеч. 128
11 6
10
B

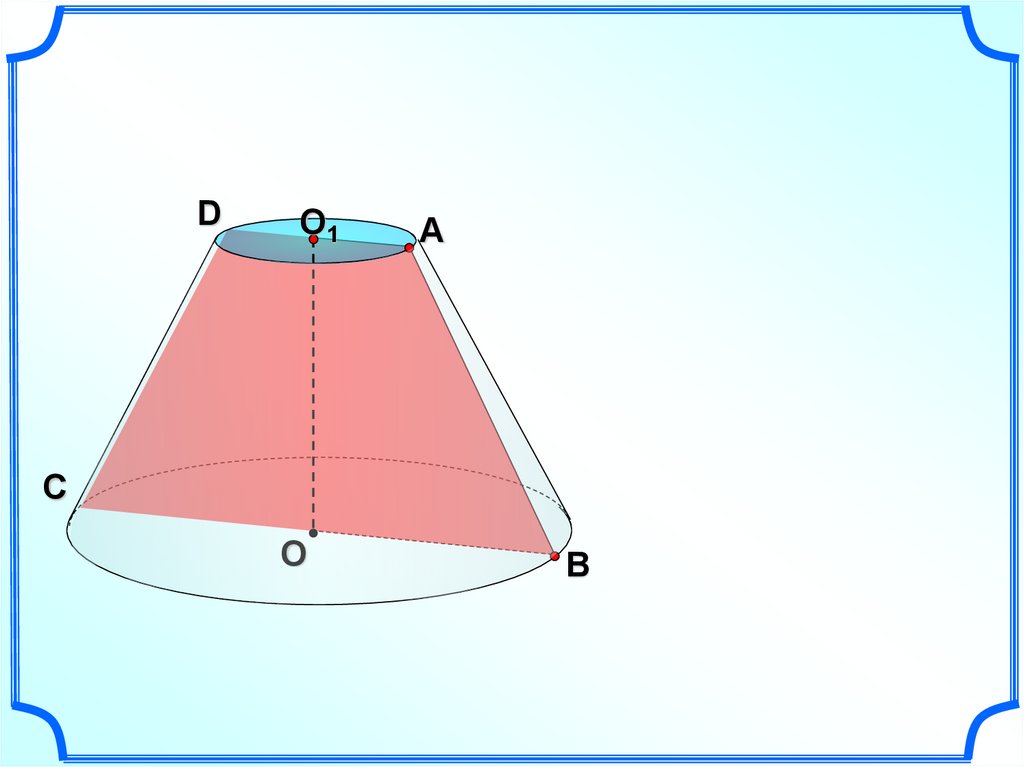
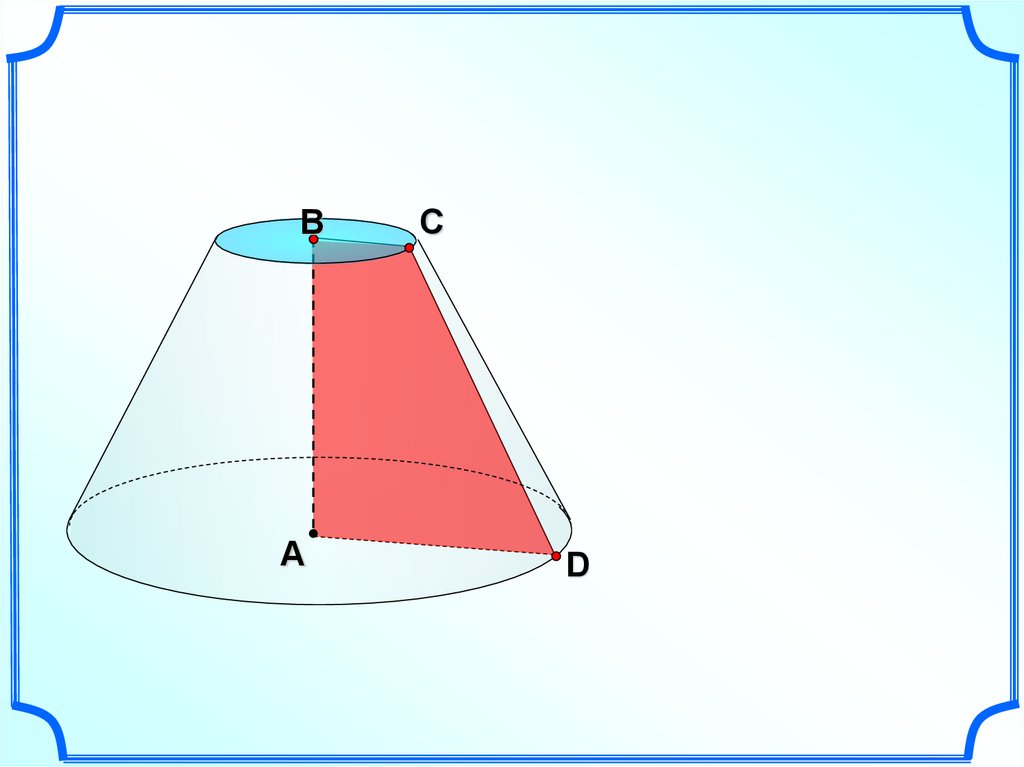
30.

D
O1
А
С
О
B

31.

В
А
С
D