аксиомы для диска

1.

Аксиомы
стереометрии.
Некоторые
следствия
из аксиом.

2.

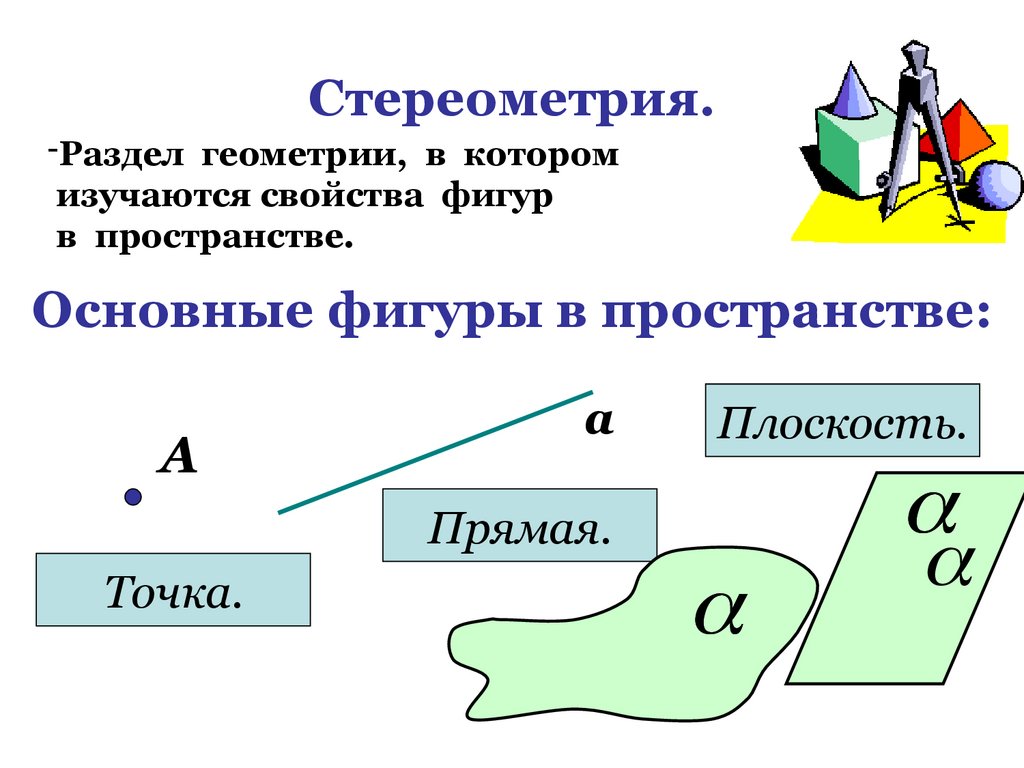
Стереометрия.
-Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Плоскость.
Прямая.

3.

СТЕРЕОМЕТРИЯ
ОБОЗНАЧЕНИЕ
точка
прямая
A, B, C, …
a, b, c, …
или
AВ, BС, CD, …
,
,
,
плоскость

4.

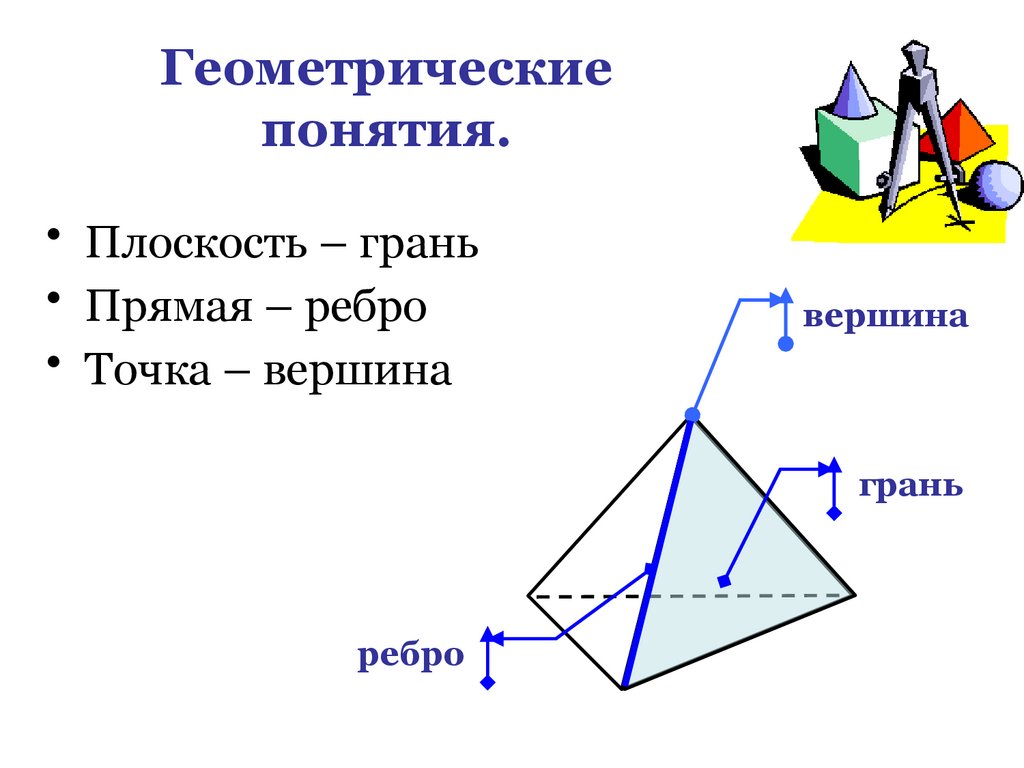
Геометрические
понятия.
• Плоскость – грань
• Прямая – ребро
• Точка – вершина
вершина
грань
ребро

5.

Аксиома
(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства

6.

АКСИОМЫ
А1. Через любые три точки, не
лежащие на одной прямой,
проходит плоскость, и притом
только одна
А2. Если две точки прямой
лежат в плоскости, то все
точки прямой лежат в этой
плоскости
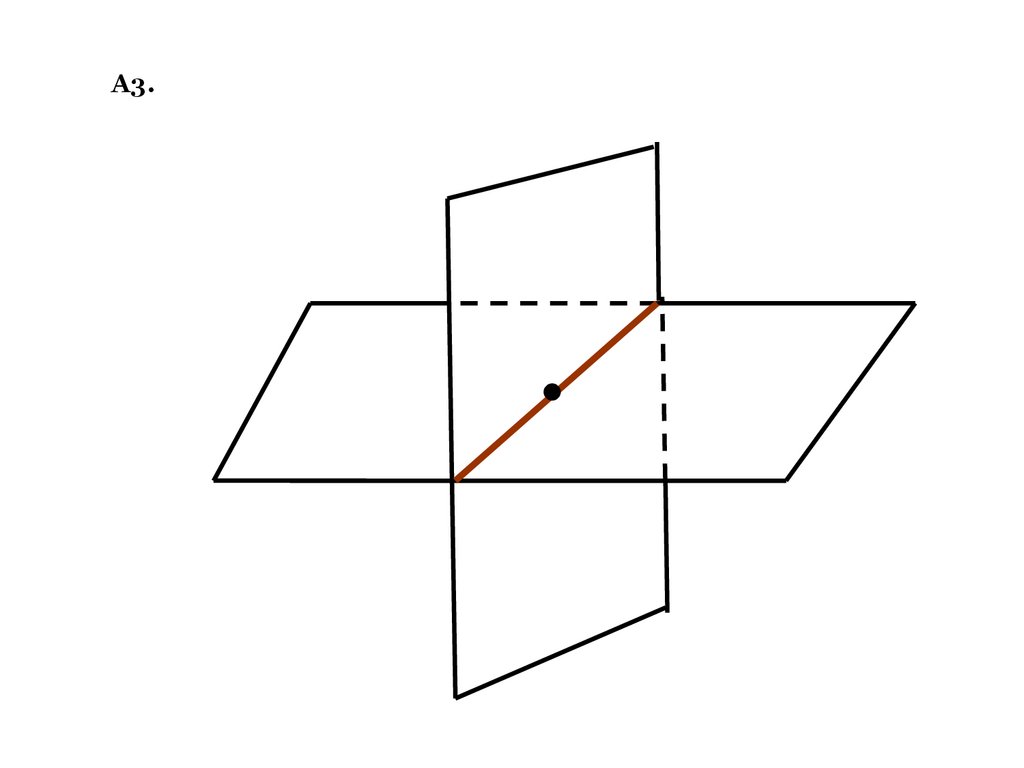
А3. Если две плоскости
имеют общую точку, то они
имеют общую прямую, на
которой лежат все общие
точки этих плоскостей.

7.

А3.

8.

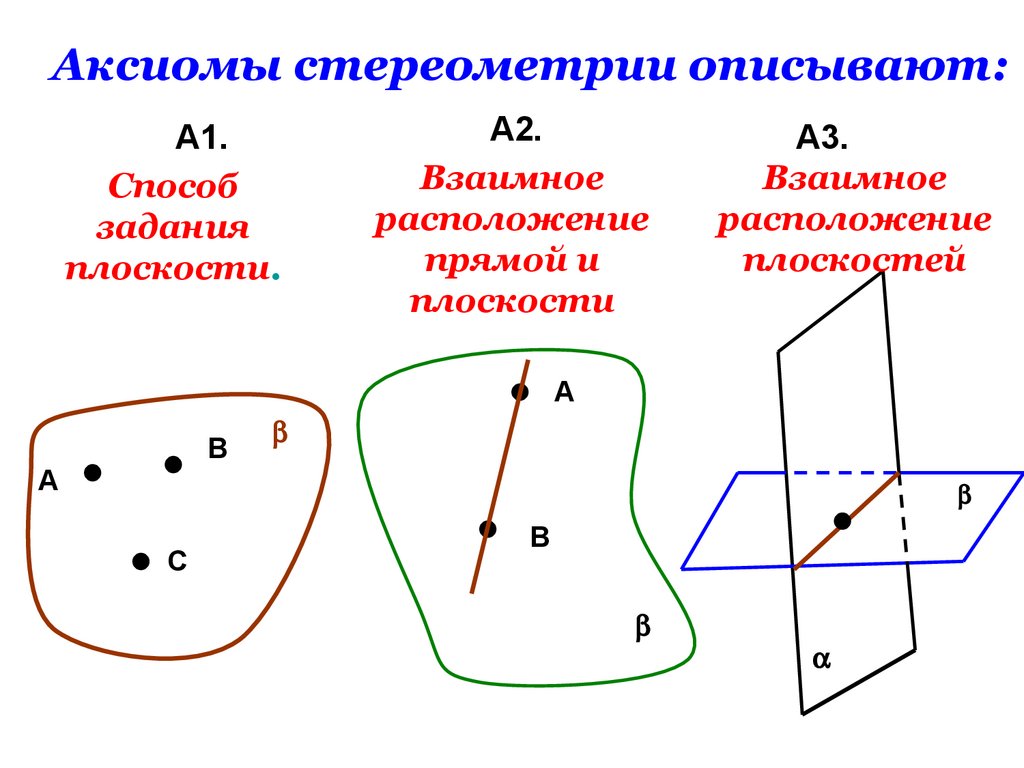
Аксиомы стереометрии описывают:
А1.
Способ
задания
плоскости.
А2.
Взаимное
расположение
прямой и
плоскости
А3.
Взаимное
расположение
плоскостей
А
В
А
b
b
С
В
b
a

9.

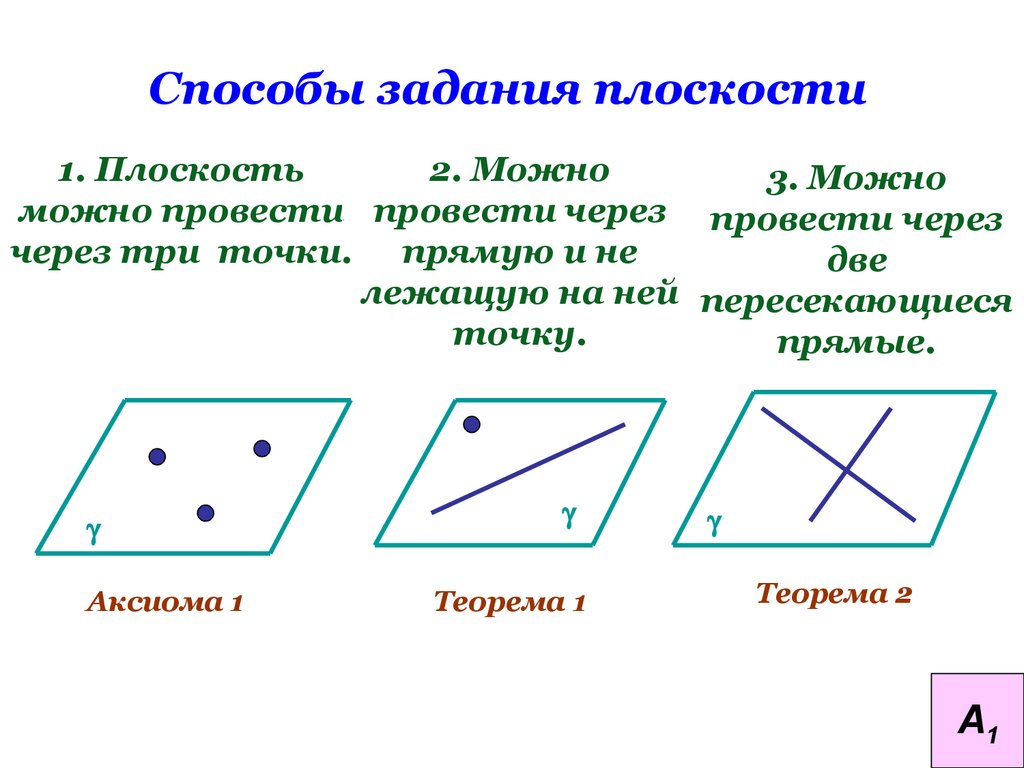
Способы задания плоскости
1. Плоскость
2. Можно
3. Можно
можно провести провести через провести через
через три точки. прямую и не
две
лежащую на ней пересекающиеся
точку.
прямые.
g
Аксиома 1
g
Теорема 1
g
Теорема 2
А1

10.

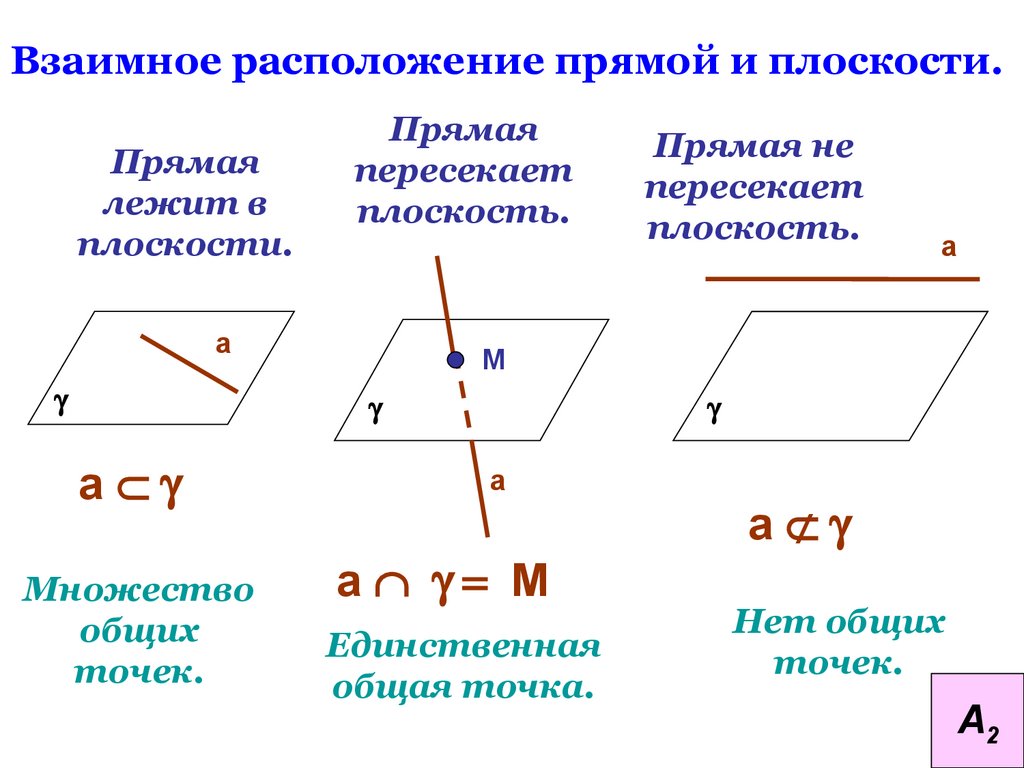
Взаимное расположение прямой и плоскости.
Прямая
лежит в
плоскости.
Прямая
пересекает
плоскость.
а
g
Множество
общих
точек.
а
М
g
аÌg
Прямая не
пересекает
плоскость.
g
а
аÇ g= М
Единственная
общая точка.
аËg
Нет общих
точек.
А2

11.

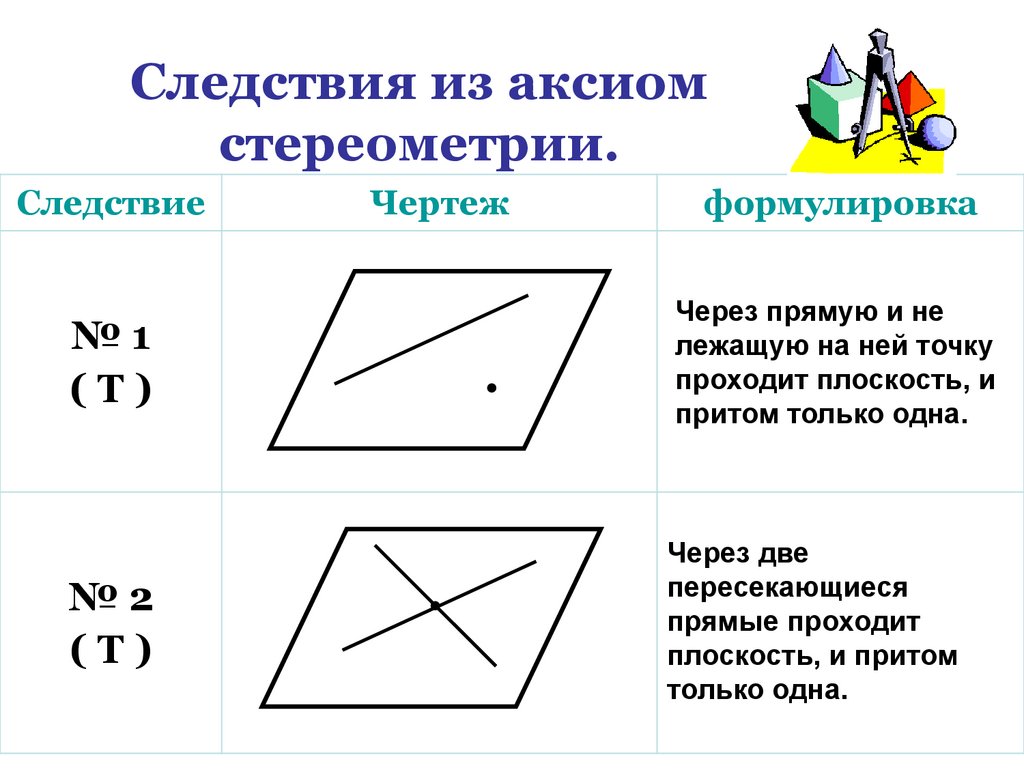
Следствия из аксиом
стереометрии.
Следствие
Чертеж
формулировка
№1
(Т)
Через прямую и не
лежащую на ней точку
проходит плоскость, и
притом только одна.
№2
(Т)
Через две
пересекающиеся
прямые проходит
плоскость, и притом
только одна.