Н . Интеграл

1.

Математика
Преподаватели:
Кормилицына Елена Анатольевна,
Федотова Екатерина Алексеевна

2.

Тема 9.
Неопределённы
й интеграл

3.

План лекции
1. Понятие первообразной.
2. Понятие неопределённого
интеграла.
3. Свойства неопределённого
интеграла.

4.

1. Понятие первообразной
В дифференциальном
исчислении была решена
следующая задача: по данной
функции найти её
производную. То есть действие
дифференцирования функции
на некотором промежутке Х

5.

6.

7.

8.

Пример
Является ли функция
3
x
F ( x)
3
первообразной для функции
f ( x) x ?
2

9.

Отыскание по данной
функции её первообразной
составляет одну из основных
задач интегрального
исчисления. Естественно,
возникает следующий вопрос:
для всякой ли функции
существует первообразная?

10.

Убедительный ответ на этот
вопрос для достаточно широкого
класса функций даёт следующая
теорема.
Теорема. Любая непрерывная на
промежутке Х функция имеет на
этом промежутке первообразную.

11.

Замечание!
Если функция, для которой
мы ищем первообразную,
имеет точки разрыва, то мы
будем её рассматривать только
на тех интервалах, где она
непрерывна.

12.

13.

14.

Поэтому, естественно,
возникает вопрос об
отыскании всех
первообразных для данной
функции. Исчерпывающий
ответ на этот вопрос даёт
следующая теорема.

15.

16.

17.

2. Понятие неопределённого
интеграла.
Из теоремы выше следует, что
первообразная определена с
точностью до некоторой
константы C, то есть
определена неоднозначно.

18.

Для того, чтобы
эта задача была однозначно
определена вводят понятие
неопределённого интеграла.
И так, мы выясняли, что
если функция имеет
первообразную на промежутке X,
то она имеет

19.

20.

21.

22.

23.

x – переменная интегрирования,
dx – дифференциал (он
показывает по какой переменной
ведётся интегрирование).
Действие отыскания
неопределённого интеграла
или, что тоже самое

24.

нахождение всех
первообразных от данной
функции, называется
интегрированием этой
функции. Интегрирование
является обратным процессом
дифференцирования.

25.

26.

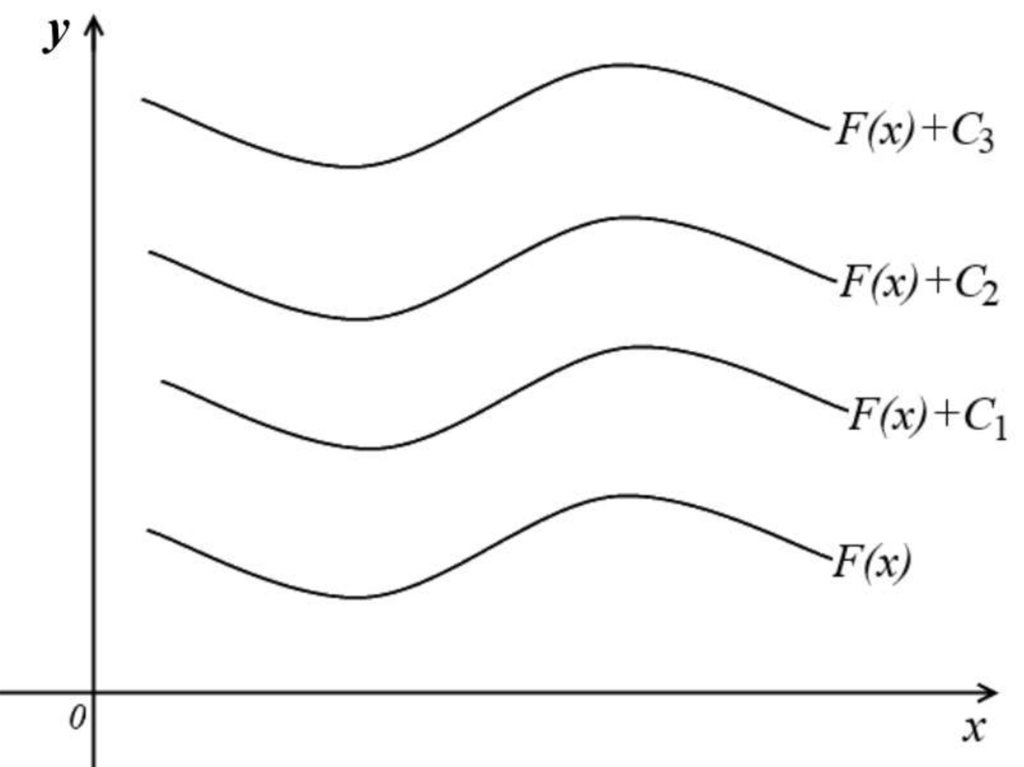
где каждому конкретному
числовому значению постоянной
C соответствует определенная
кривая из указанного семейства.
График каждой кривой
из семейства называется
интегральной кривой.

27.

28.

3. Свойства неопределённого
интеграла
Неопределённый интеграл
обладает рядом свойств.
Далее сформулируем две
теоремы, в которых приведём
основные свойства
неопределённого интеграла.

29.

30.

Подведём итог этой теоремы:
− первое и второе свойство
позволяет проводить проверку
интегрирования. Чтобы проверить
правильность интегрирования,
достаточно вычислить
производную(дифференциал)
полученного результата.

31.

Если полученная в результате
дифференцирования функция
окажется равной
подынтегральной
функции(подынтегральному
выражению), то это будет
означать, что интегрирование
проведено верно;

32.

− третье свойство
неопределенного интеграла
позволяет по известному
дифференциалу функции найти
ее первообразную. На этом
свойстве основано
непосредственное вычисление
неопределенных интегралов.

33.

34.

35.

36.

СПАСИБО ЗА
ВНИМАНИЕ!