4. Анализ сост БзП по данн экспл

1.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА)
Анализ состояния БзП по данным эксплуатации
Доцент кафедры БП и ЖД,
к.т.н., с.н.с. Пахомов О.В. 1

2.

1. Оценка уровня БзП по данным эксплуатации
2. Статистическая оценка степени опасности факторов
3. Количественная оценка опасности ОС экспертным методом
4. Ранжирование опасных факторов методом попарного сравнения
5. Оценка соответствия фактического уровня БзП требованиям Норм ЛГ

3.

1. Оценка уровня БзП по данным эксплуатации
Показатели:
Q
nАП
,
N
Qt
nАП
,
t
TАП
t
, PБП
e nАП ,
nАП
где n АП - количество АП , N – количество полетов, t ∑ - суммарный налет ЛА за период эксплуатации.
Так как статическая оценка n* АП – величина случайная, необходимо при заданной
доверительной вероятности β определить доверительный интервал
Нижняя и верхняя границы n АП 1 и n АП 2
n АП 1 ≤ n* АП ≤ n АП 2.
2
определяются с использованием таблицы величины
= F ( β, f )
1 2
1
f1 2nАП ; f 2 2(nАП 1)
1 ( f1 ) nАП 12 ( f 2 ) , где
2
2
2
2
1
При f 30 и = 0,95
02,975 ( f1 ) ( 2 f1 1,96) 2 ;
эти величины
рассчитывают по
формулам:
2
1
02,025 ( f1 ) ( 2 f 2 1,96) 2 .
2
Границы доверительных интервалов статистических оценок показателей БзП определяются по формулам:
Q1
nАП1
TАП1
N
, Q2
nАП2
N
; Qt1
t
t
, TАП2 ;
nАП2
nАП1
PБП1 e
nАП2
,
PБП 2 e
nАП1
.
nАП1
t
, Qt 2
nАП2
t
,

4.

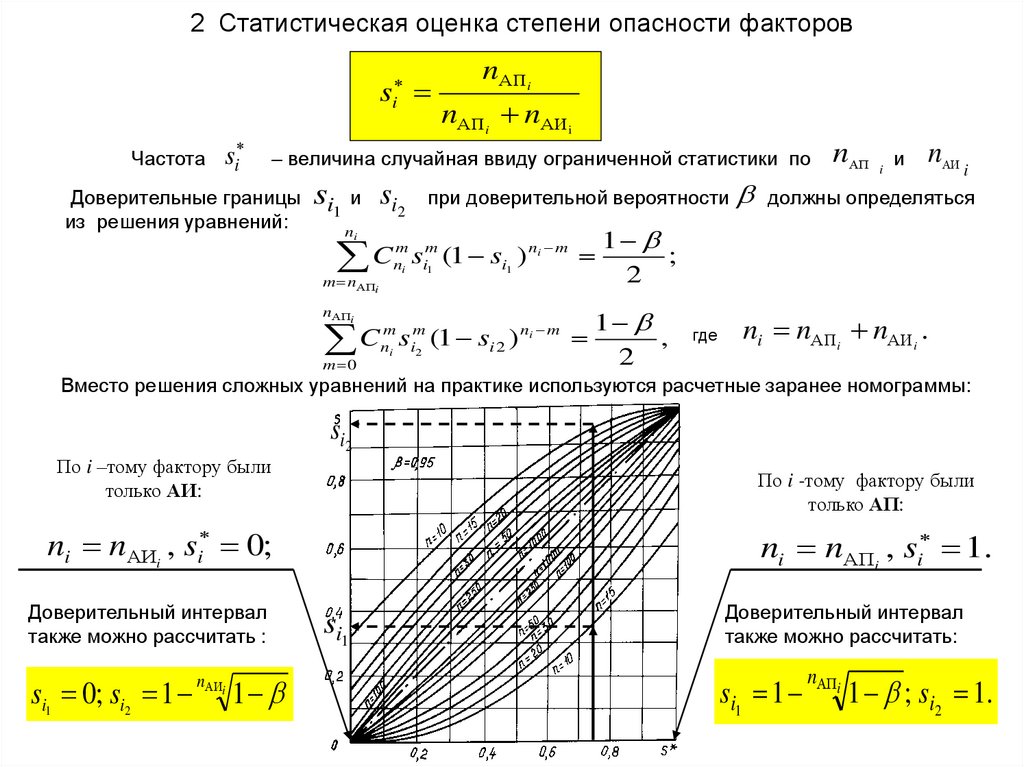
2 Статистическая оценка степени опасности факторов
si
Частота
si
nАПi
nАПi nАИi
– величина случайная ввиду ограниченной статистики по
Доверительные границы si и
1
из решения уравнений:
n
si2
при доверительной вероятности должны определяться
Cnmi sim1 (1 si1 ) ni m
i
m nАПi
nАПi
C s (1 s )
m 0
m m
ni i2
nАП i и nАИ i
i2
ni m
1
;
2
1
,
2
где
ni nАПi nАИi .
Вместо решения сложных уравнений на практике используются расчетные заранее номограммы:
si2
По i –тому фактору были
только АИ:
По i -тому фактору были
только АП:
ni nАИi , si 0;
Доверительный интервал
также можно рассчитать :
si1 0; si2 1 АИi 1
n
ni nАПi , si 1.
si1
Доверительный интервал
также можно рассчитать:
n
si1 1 АПi 1 ; si2 1.

5.

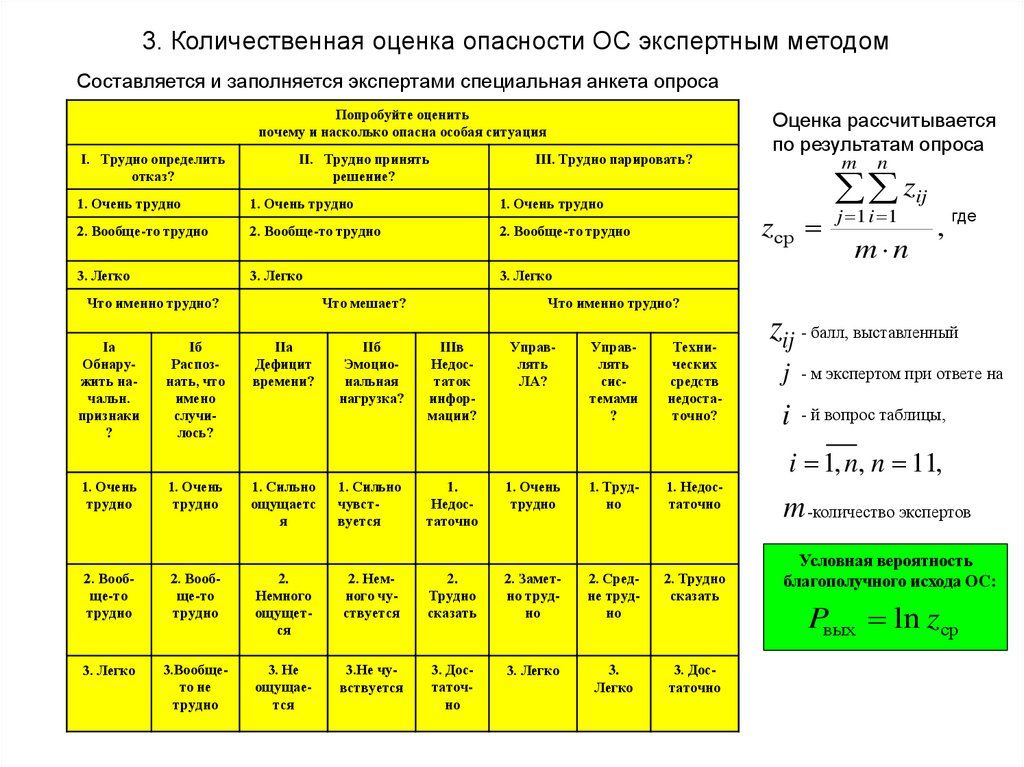
3. Количественная оценка опасности ОС экспертным методом
Составляется и заполняется экспертами специальная анкета опроса
Попробуйте оценить
почему и насколько опасна особая ситуация
I. Трудно определить
отказ?
II. Трудно принять
решение?
III. Трудно парировать?
1. Очень трудно
1. Очень трудно
1. Очень трудно
2. Вообще-то трудно
2. Вообще-то трудно
2. Вообще-то трудно
3. Легко
3. Легко
3. Легко
Что именно трудно?
Iа
Обнаружить начальн.
признаки
?
Iб
Распознать, что
имено
случилось?
Что мешает?
IIа
Дефицит
времени?
IIб
Эмоциональная
нагрузка?
Оценка рассчитывается
по результатам опроса
m
zср
n
zij
j 1 i 1
m n
,
где
Что именно трудно?
IIIв
Недостаток
информации?
Управлять
ЛА?
Управлять
системами
?
Технических
средств
недостаточно?
zij - балл, выставленный
j - м экспертом при ответе на
i - й вопрос таблицы,
i 1, n, n 11,
1. Очень
трудно
1. Очень
трудно
1. Сильно
ощущаетс
я
1. Сильно
чувствуется
1.
Недостаточно
1. Очень
трудно
1. Трудно
1. Недостаточно
2. Вообще-то
трудно
2. Вообще-то
трудно
2.
Немного
ощущется
2. Немного чуствуется
2.
Трудно
сказать
2. Заметно трудно
2. Средне трудно
2. Трудно
сказать
3. Легко
3.Вообщето не
трудно
3. Не
ощущается
3.Не чувствуется
3. Достаточно
3. Легко
3.
Легко
3. Достаточно
m -количество экспертов
Условная вероятность
благополучного исхода ОС:
Pвых ln zср

6.

4. Ранжирование опасных факторов i и j методом попарного сравнения
Сравнение i- и j-того ОФ может проводится
по различными критериям:
Составляется матрица сравнения ОФ:
ОФ
1
2
…
i
…
j
…
n
1
–
-I
…
I
…
0
…
0
2
I
–
…
-I
…
0
…
-I
:
.
…
…
–
…
…
…
…
…
i
-I
I
…
–
…
-I
…
0
:
.
…
…
…
…
–
…
…
…
j
0
0
…
I
…
–
…
I
:
.
…
…
…
…
…
…
–
…
n
0
I
…
0
…
-I
…
–
∑1
q
∑i
∑j
nАП nАИ
;
N
3 - степени опасности
s
nАП
;
nАП nАИ
4 - экспертным методом;
5 - по критерию статистического сравнения
∑n
–1, если Q i > Q j
1, если Q i < Q j
Наиболее аварийному ОФ соответствует наименьшая
сумма баллов ∑ n в строке.
n i и n j;
2 - вероятности (частоте) появления ОФ в полете
0, если Q i = Q j
В каждую i j ячейку
матрицы заносится:
1 - количество случаев появления ОФ в полете
1
1 где n j > n i
и 2 ( n j ni ),
2
2
При уровне значимости α = 0,05
величина критерия u 0,95 = 1,64.
Если u < 1,64, принимается гипотеза
Qj=Qi
Если u > 1,64, принимается
альтернативная гипотеза
Qj>Qi

7.

5. Оценка соответствия фактического уровня БзП требованиям Норм ЛГ
В «Нормах летной годности самолетов транспортной категории» (АП-25) нормируются частоты ОС:
Q кс норм = 10-7 на один час полета;
Q ас норм = 10-6 на один час полета;
Q сс норм = 10-4 на один час полета;
Q ууп норм = 10-3 на один час полета.
По результатам сравнения фактической (рассчитаной по статистическим данным эксплуатации)
частоты Q ос* с нормативной Q ос норм возможно принятие следующих гипотез:
- нулевой гипотезы – фактический уровень БзП соответствует заданному (Q ос* = Q ос норм);
- альтернативной гипотезы 1 – фактический уровень БзП меньше заданного (Q ос* > Q ос норм);
- альтернативной гипотезы 2 – фактический уровень БзП больше заданного (Q ос* < Q ос норм).
Так как частота Q ос рассчитывается через количество n ос, задача сводится к сравнению расчета
статистической оценки количества ОС в полете n* ос с нормативным значением n ос норм.
Нормативная величина n ос норм рассчитывается по формуле:
n ос норм = t ∑ · Q ос норм,
где t ∑ - суммарный налет; Q ос норм - заданная нормами частота ОС.
Статистическая оценка n* ос – величина случайная, поэтому надо определить нижнюю и верхнюю
границы ее доверительного интервала n* ос н и n* ос в.
Выбор одной из трех гипотез определяется соотношением границ доверительного интервала и n ос норм:
1) n ос норм < n* ос н
2) n ос норм = n* ос н, n* ос в
3) n ос норм > n* ос в
(гипотеза 1)
0
n* ос н
(гипотеза 0)
n* ос
Доверительный интервал
(гипотеза 2)
n* ос в
n ос

8.

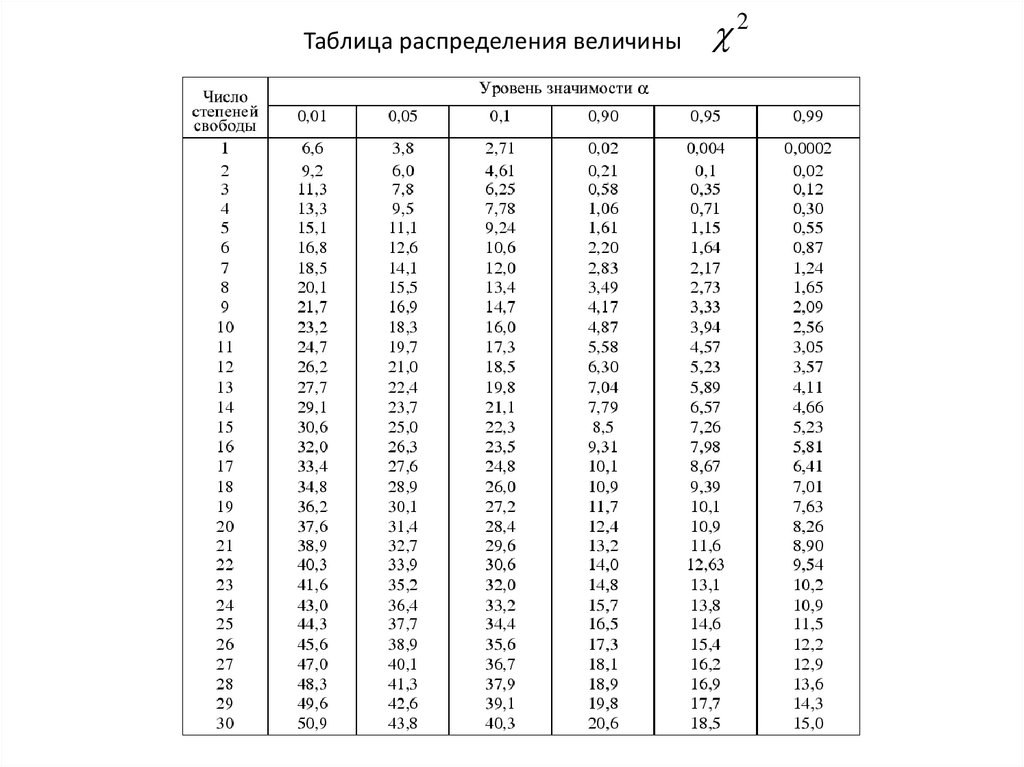
При пуассоновском распределении n ос для расчета доверительных интервалов применяется
распределение хи-квадрат*
и уровня значимости α .
2 , которое задается таблично для «числа степеней свободы» f
Нижняя и верхняя границы доверительного интервала рассчитывается по формулам:
1 2
1 ( f1 ) ,
2
1
n ос в 2 ( f 2 ) ,
2
n ос н
f1 2nос
f 2 2(nос 1)
При n ос ≥ 15 ( f 30 ) и доверительной вероятности
= 0,95 границы можно
рассчитать по приближенным формулам:
1
( 2 f1 1,96) 2 ;
2
1
02, 025 ( f 2 ) ( 2 f 2 1,96) 2 .
2
02,975 ( f1 )
*Распределение аналогично нормальному распределению
случайной величины, но имеет только положительные значения,
как и число n ос .
2

9.

Таблица распределения величины
2