Похожие презентации:
Дисперсионный анализ
1. ДИСПЕРСИОННЫЙ АНАЛИЗ
2.
• Дисперсионный анализ — разделматематической статистики,
связанный с методами выявления
влияния отдельных факторов на
результат эксперимента
(физического, производственного,
экономического).
3.
• Дисперсионный анализ исходит изположения о том, что существенность
фактора в определенных условиях
характеризуется его вкладом в
дисперсию результата.
• Английский статистик Р. Фишер,
разработавший этот метод, определил
его как “отделение дисперсии,
приписываемой одной группе причин,
от дисперсии, приписываемой другим
группам”.
4.
Анализ производится следующим образом.1
•Сначала группируют
совокупность наблюдений по
факторному признаку, находят
среднее значение результата
и дисперсию по каждой
группе.
5.
2• Затем определяют общую
дисперсию и вычисляют, какая
доля ее зависит от условий,
общих для всех групп, какая —
от исследуемого фактора, а
какая — от случайных причин.
6.
3• И наконец, с помощью специального
критерия определяют, насколько
существенны различия между
группами наблюдений и,
следовательно, можно ли считать
ощутимым влияние тех или иных
факторов.
7.
• Дисперсионный анализ применяется впланировании эксперимента и в ряде
исследований, где он служит, в
частности, предварительным этапом к
регрессионному анализу
статистических данных, поскольку
позволяет выделить относительно
небольшое (но достаточное для целей
исследования) количество параметров
регрессии.
8.
В дисперсионном анализерассматривается эксперимент, в
котором производится
варьирование при фиксированных
уровнях некоторыми факторами. В
результате возникает продукт с
выходным параметром, имеющим
вероятностный характер.
9.
Обычно принимаетсяпредположение о
нормальном законе
распределения выходной
характеристики этого
параметра.
.
10.
• Нормальное распределениевызвано погрешностью
измерений, влиянием
контролируемых условий и т.д.,
оно проявляется при проведении
повторных опытов (партии
опытов) в «одной точке» - при
каждом конкретном сочетании
уровней факторов.
11.
12.
•Вторым предположениемявляется
однородность дисперсий в
«различных точках» - при
различных сочетаниях
уровней факторов.
13.
Для удобства в упрощенномвиде рассмотрим
однофакторный
дисперсионный анализ, а
затем двухфакторный и
трехфакторный.
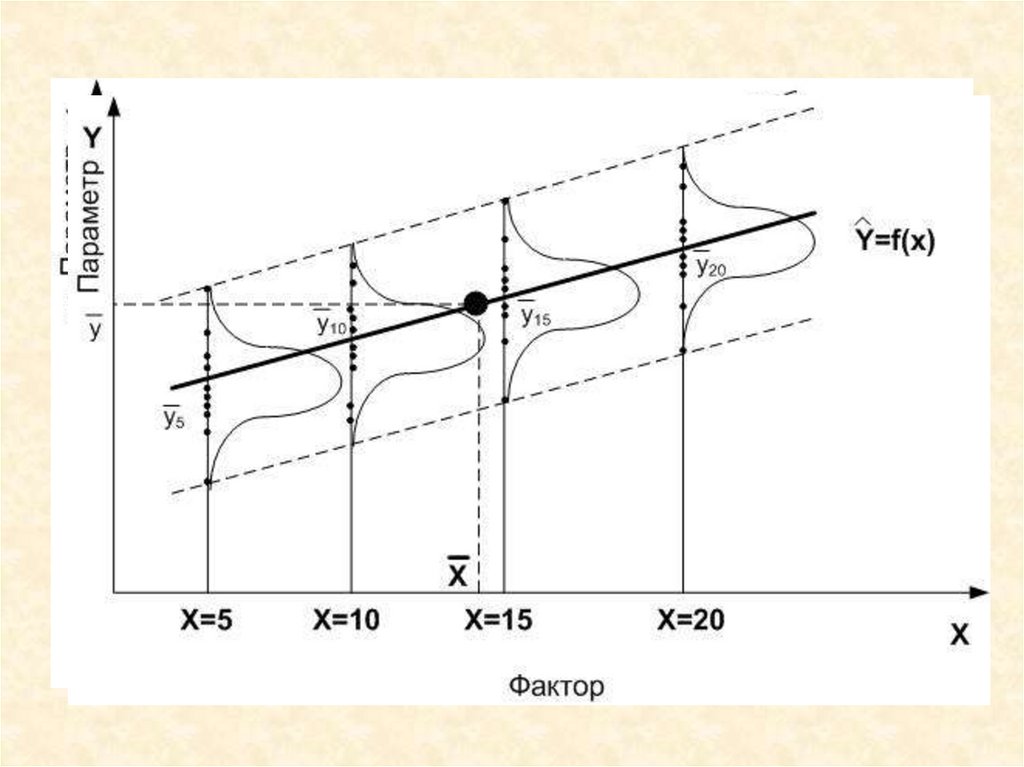
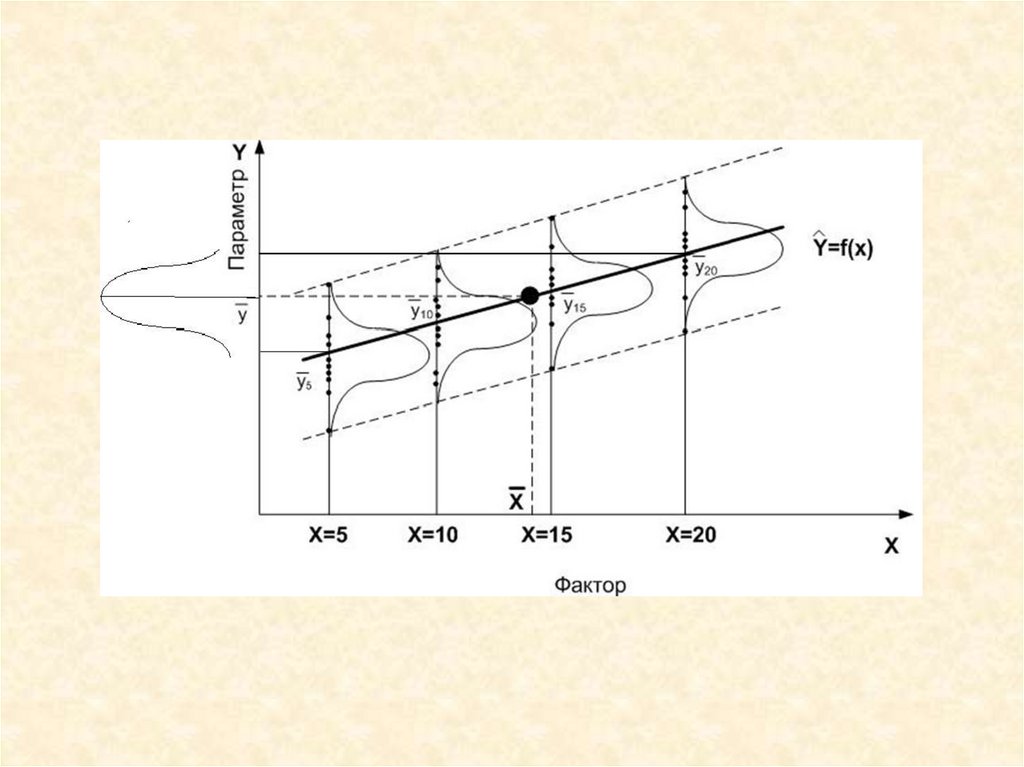
14. Однофакторный эксперимент
15.
Проверяют однородность рядадисперсий по критерию Кохрена .
Если расчетное значение критерия
окажется больше табличного
значения при принятом уровне
значимости α и количестве
наблюдений,
то гипотеза об однородности
дисперсий отвергается.
k
Gmax [ Si2 ]max / Si2
i 1
16.
• После подтверждения гипотезы ободнородности этих дисперсий находят
общее среднее
1 k
y
yi .
k i 1
• Далее вычисляются дисперсии:
- характеризующую рассеяние по факторам;
S 2 n - остаточную дисперсию, характеризующую
рассеяние внутри партий;
S 2 - полную (общую) дисперсию, отражающую
общее рассеяние как внутри партий, так и за счет
изменения уровня фактора
S 2A
17.
S2
A
1 k
2
( y i y) .
k 1 i 1
f1 k 1.
k
S
2
n
k n
1
2
( yij y i )
k (n 1) i 1 j 1
Si
2
i 1
k
;
f 2 k (n 1).
k n
1
2
S
( yij y ) ;
k n 1 i 1 j 1
2
f 2 k n 1.
18.
19.
20.
Для выяснения вопроса о том, сказываетсяли влияние фактора А, или это влияние
несущественно по сравнению с разбросом
внутри партии, проверяют однородность
дисперсий S 2 Aи S 2 n при помощи критерия
Фишера.
2
2
F S A/S n
Если это отношение
окажется меньше
табличного значения F1 , найденного для числа
степеней свободы f1 и f 2 и уровня значимости
α, то влияние фактора несущественно.
21.
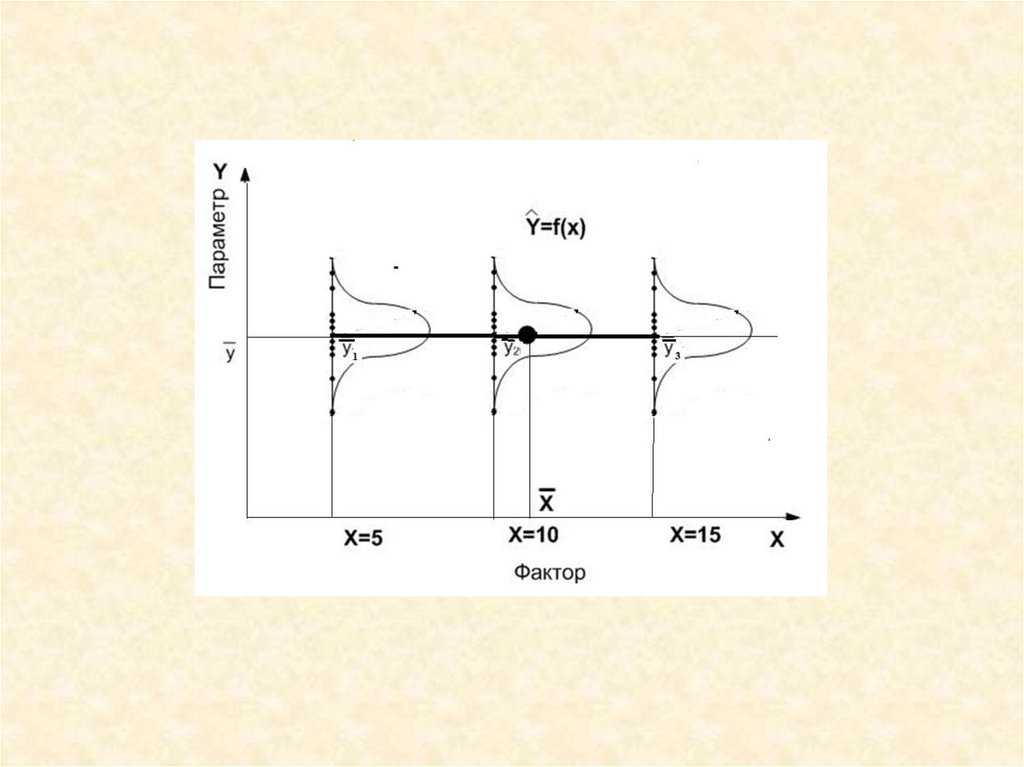
Если влияние фактора несущественно, товсе результаты испытаний принадлежат
одной генеральной совокупности,
распределенной нормально с параметрами
2
и a
Их точечные оценки соответственно равны
2
S и y , а интервальные для (верхняя и
нижняя границы)
k
ni 1
S t , f
a В. Н . y
, В ( Н ) S Z 2(1) i 1 k
;
k
ni
ni
i 1
i 1
22.
Если влияние фактора существенно, тосчитается, что есть k нормально
распределенных совокупностей, каждая из
2
которых имеет дисперсию с разными
средними значениями a i. Точечной
2
2
S
оценкой
является
n , а оценкой
средних - выборочные средние y i .
Доверительные интервалы для a i и
имеют следующий вид:
S n
аi В.Н . yi
t , f ,
ni
k
BН S n Z 2(1)
ni k
i 1
k
ni k 1
i 1
;
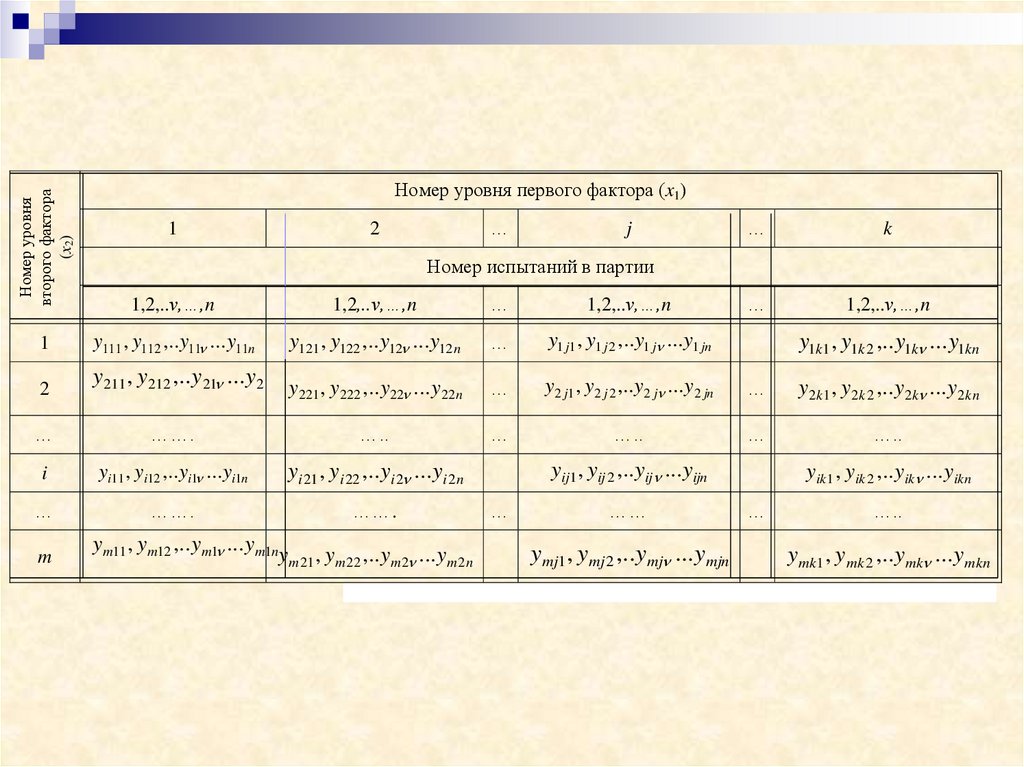
23. Двухфакторный дисперсионный анализ
24. Ниже приведены результаты испытаний для двухфакторного анализа. Один из факторов x1 имеет k уровней, другой x2 – m. При каждой
комбинации уровнейпроизводится одинаковое
количество n опытов.
25.
Номер уровнявторого фактора
(x2)
Номер уровня первого фактора (x1)
1
…
2
j
…
k
…
1,2,..ν,…,n
Номер испытаний в партии
1,2,..ν,…,n
1,2,..ν,…,n
…
1,2,..ν,…,n
1
y111 , y112 ,..y11 ...y11n
y121 , y122 ,..y12 ...y12 n
…
y1 j1 , y1 j 2 ,..y1 j ...y1 jn
2
y 211 , y 212 ,..y 21 ...y 21n y , y ,..y ...y
221
222
22
22 n
…
y2 j1 , y2 j 2 ,..y2 j ...y2 jn
…
y2 k1 , y2 k 2 ,..y2 k ...y2 kn
…
…..
…
…..
…
…….
…..
i
yi11 , yi12 ,..yi1 ...yi1n
yi 21 , yi 22 ,..yi 2 ...yi 2 n
…
…….
…….
m
ym11 , y m12 ,..y m1 ...ym1n
y m 21 , y m 22 ,..y m 2 ...y m 2 n
y1k1 , y1k 2 ,..y1k ...y1kn
yij1 , yij 2 ,..yij ...yijn
…
……
ymj1 , ymj 2 ,..ymj ...ymjn
yik 1 , yik 2 ,..yik ...yikn
…
…..
ymk1 , y mk 2 ,..ymk ...y mkn
26. Сначала рассчитываются средние значения случайной величины Y для каждой партии опытов:
1 ny ij yij ;
n 1
затем средние значения по графам y 0 j (по
фактору x2) и по строчкам y i (по фактору x1):
1 k
1 m
y i yij ;
y 0 j yij ;
k j 1
m i 1
и среднее значение наблюдений
k
1 m
y ( y j ) / k или
y ( yi ).
j 1
m i 1
27.
Расчет средних значений и дисперсийНомер строки
(уровня фактора
x2)
Номер столбца (уровня фактора x1)
Среднее
по
строкам
1
2
…
j
…
k
1
y 11
y12
…
y1 j
…
y 1k
y1
2
y 21
y 22
…
y2 j
…
y 2k
y2
…
…
…
…
…
…
…
i
y i1
y i2
…
y ij
…
y ik
…
yi
…
…
…
…
…
…
…
…
m
y m1
y m2
…
y mj
…
y mk
ym
Среднее по
столбцам
y1
y2
…
yj
…
yk
y
nij
1 n
1
2
y ij yij ; S 2 ij
( yij y ij ) ;
n 1
nij 1 i , j 1
1 k
yi y j ;
k j 1
yj
1 m
yi ;
m i 1
1 m
y ( y i ).
m i 1
28. Далее вычисления рассчитываются дисперсии
2S х1
- между средними по графам
2
S х2
- между средними по строкам
2
S x1x2
- при взаимодействии между
факторами
2
Sn
2
- внутри партии (остаточная)
S - полная (общая) дисперсия)
29.
Компонентадисперсии
Между
средними по
графам
Между
средними по
строкам
При
взаимодействи
и между
факторами
Внутри партии
(остаточная)
Полная
(общая)
дисперсия
Число степеней
свободы
Сумма квадратов
k
Q1 m n ( y j y ) 2
j 1
m
Q2 k n ( y i y) 2
i 1
m k
Q3 n ( y ij y i y j y ) 2
i 1 j 1
m k n
Q4 ( y ij
i 1 j 1 1
y ij ) 2
k n
2
( n 1) S ij
i 1 j 1
f1 k 1
S х21
f 2 m 1
S х22
f 3 (k 1)
(m 1)
( yij y )
i 1 j 1 1
2
f S k m n 1
Q1
k 1
Q2
m 1
S х21х2
Q3
(k 1) (m 1)
f 4 k m (n 1) S 2
n
Q Q1 Q2 Q3 Q4
m k n
Дисперсия
S
2
Q4
k m(n 1)
Q
k m n 1
30. Далее с помощью критерия Фишера проверяют гипотезу об отсутствии взаимодействия между исследуемыми факторами.
F S 2 / S 2x1x2
n
Расчетное значение критерия
сопоставляют с табличным, найденным
для уровня значимости α и числа
степеней свободы
f 3 (k 1) (m 1) и
f 4 k m(n 1)
31. Если расчетное значение критерия больше табличного, то гипотеза о независимости факторов x1 и x2 отвергается. Если же оно
меньше, то гипотеза оботсутствии связи подтверждается.
32. Далее проверяют значимость влияния обоих факторов на исследуемую величину Y. Для этого предварительно объединяют оценки
дисперсийвзаимодействия между факторами и
остаточную
S (Q3 Q4 ) /( f 3 f 4 ).
2
0
и вычисляют отношения
F1
2
S х1
2
/ S0 ,
и
F2
2
S х2
2
/ S0 ,
33. Если расчетные значения больше табличных, то влияние факторов значимо. В этом случае мы имеем дело с k*m нормально
распределеннымигенеральными совокупностями с общей
2
дисперсией и разными значениями
aij
Их оценками служат выборочная
дисперсия S20
и выборочные средние
для каждой комбинации факторов y
ij
34. Если расчетные значения критериев меньше табличных, то влияние обоих факторов на параметр Y не значимо. В этом случае мы имеем
дело с однойгенеральной совокупностью с
2
дисперсией и математическим
ожиданием
Оценкой а служит общее выборочное
среднее по строкам и столбцам y
Оценкой является полная (общая)
2
выборочная дисперсия S
2
35. Возможны и другие ситуации. Может оказаться, что один фактор значим, а другой не значим. В этом случае мы имеем дело или с m
или k (взависимости от того, какой фактор
значим) генеральными
совокупностями.
36. Пример двухфакторного дисперсионного анализа
37.
Исходные для примера получены спомощью программы «Модел. вероят.
процессов.xls» при сочетании
факторов, приведенных в ниже.
В примере Y – результирующий
параметр, который регистрируется при
проведении численных экспериментов,
а х1 и х2 – факторы, влияние которых
требуется исследовать.
38.
Необходимо провести девять партийэкспериментов по 10 опытов в
каждой партии. Исследование
предусматривает испытания на трех
уровнях первого фактора xn1 xср1,, xv1
(нижнем, среднем и верхнем) и трех
уровнях второго фактора xn2 xср2,, xv2
(нижнего, среднего и верхнего)
В данном примере k=3, m=3, n=10.
39.
Условия проведения численныхэкспериментов
Номер уровня
второго фактора x2
1
2
3
Номер уровня первого фактора x1
1
2
3
№11 n=10 при xn1, xn2
№12 n=10 при xср1, xn2
№21 n=10 при xn1, xср2
№22 n=10 при xср1, xср2 №23 n=10 при xv1, xср2
№31 n=10 при xn1, xv2
№22 n=10 при xср1, xv2
№13 n=10 при xv1, xn2
№33 n=10 при xv1, xv2
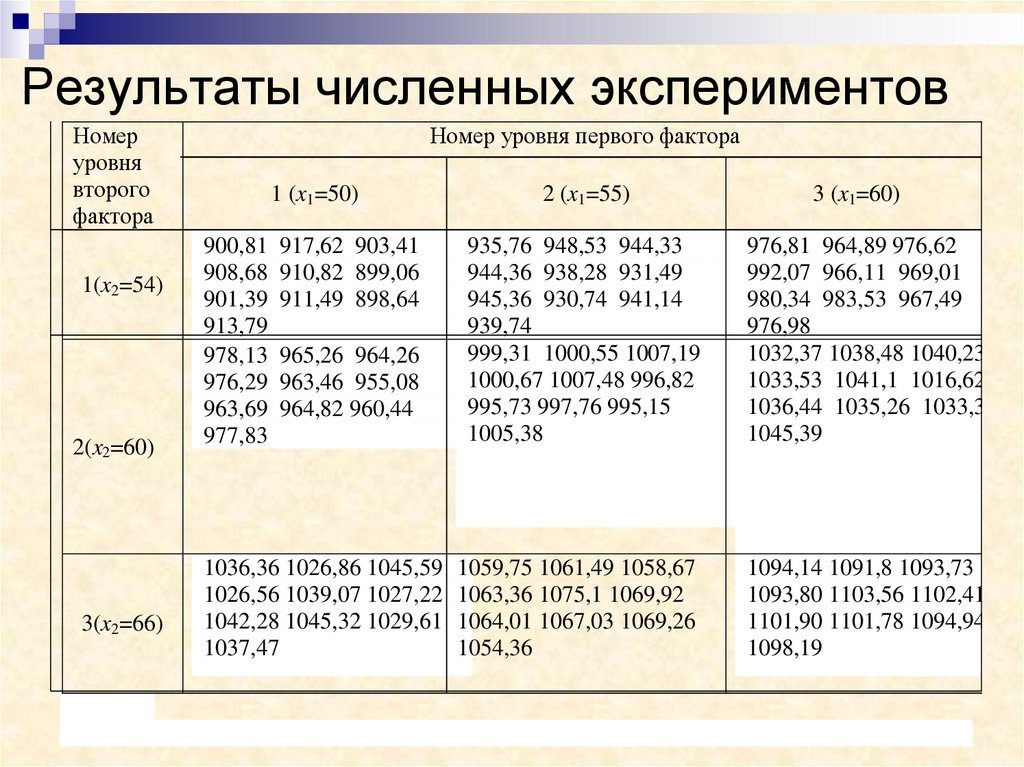
40. Результаты численных экспериментов
Номеруровня
второго
фактора
1(x2=54)
2(x2=60)
3(x2=66)
Номер уровня первого фактора
1 (x1=50)
900,81
908,68
901,39
913,79
978,13
976,29
963,69
977,83
917,62 903,41
910,82 899,06
911,49 898,64
965,26 964,26
963,46 955,08
964,82 960,44
1036,36 1026,86 1045,59
1026,56 1039,07 1027,22
1042,28 1045,32 1029,61
1037,47
2 (x1=55)
935,76 948,53 944,33
944,36 938,28 931,49
945,36 930,74 941,14
939,74
999,31 1000,55 1007,19
1000,67 1007,48 996,82
995,73 997,76 995,15
1005,38
1059,75 1061,49 1058,67
1063,36 1075,1 1069,92
1064,01 1067,03 1069,26
1054,36
3 (x1=60)
976,81 964,89 976,62
992,07 966,11 969,01
980,34 983,53 967,49
976,98
1032,37 1038,48 1040,23
1033,53 1041,1 1016,62
1036,44 1035,26 1033,39
1045,39
1094,14 1091,8 1093,73
1093,80 1103,56 1102,41
1101,90 1101,78 1094,94
1098,19
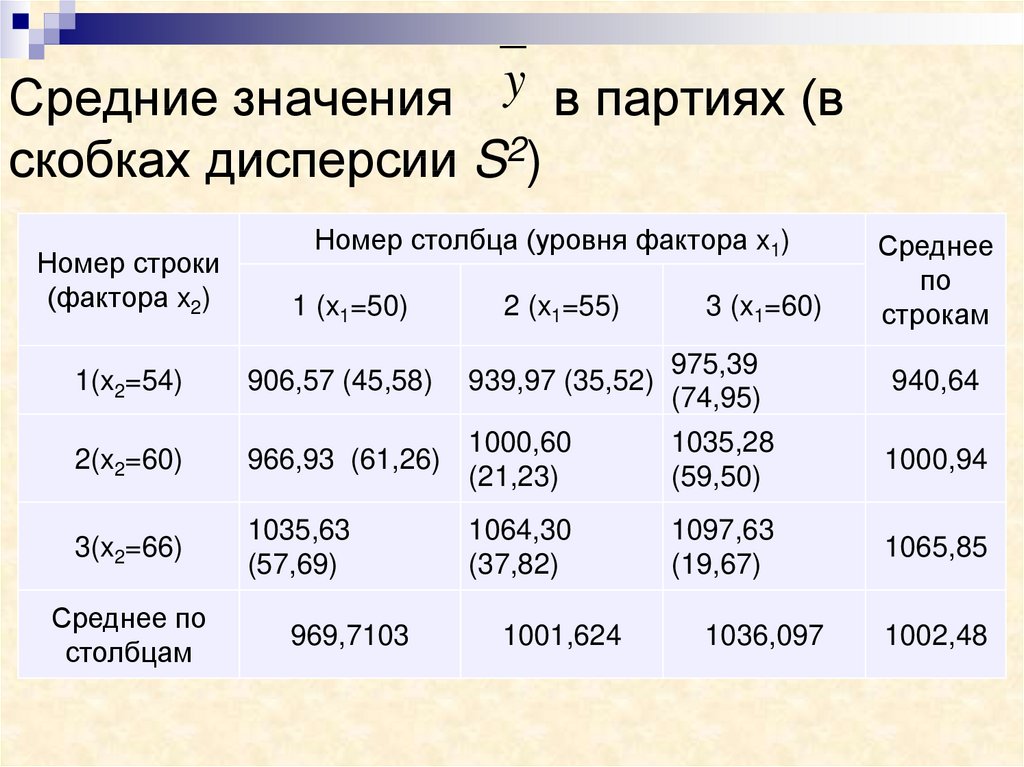
41. Средние значения в партиях (в скобках дисперсии S2)
Средние значения y в партиях (вскобках дисперсии S2)
Номер строки
(фактора x2)
Номер столбца (уровня фактора x1)
1 (x1=50)
2 (x1=55)
3 (x1=60)
Среднее
по
строкам
1(x2=54)
906,57 (45,58)
939,97 (35,52)
975,39
(74,95)
940,64
2(x2=60)
966,93 (61,26)
1000,60
(21,23)
1035,28
(59,50)
1000,94
3(x2=66)
1035,63
(57,69)
1064,30
(37,82)
1097,63
(19,67)
1065,85
Среднее по
столбцам
969,7103
1001,624
1036,097
1002,48
42. Проверка однородности дисперсий по критерию Кохрена
kGmax [ Si2 ]max / Si2 74,95/413, 22 0,18
k=9
i 1
f1 n 1 10 1 9
G 0,05 0,24
Гипотеза об
однородности
дисперсий
для разных
партий
опытов
подтверждает
ся, так как
Gmax меньше
табличного
значения
G 0, 05
43.
Расчетчисла
степеней
свободы
и дисперсий
Компонента
дисперсии
Число степеней
свободы
Сумма квадратов
Дисперсия
k
Q1 m ( x j x) 2
Между
средними по
графам
j 1
f1 k 1
3 [(969,71 - 1002,48 ) 2
3 1 2
(1001,62 - 1002,48 ) 2
(1036,1 - 1002,48 ) 2 ] 6614 ,059
Q1
k 1
6614,059
3 1
3307,029
S х21
m
Q2 k ( x i x) 2
Между
средними по
строкам
i 1
3 10 [(940,64 1002,48)
2
(1000,94 1002,48) 2
f 2 m 1
3 1 2
(1065,85 1002,48) 2 ]
23526,36
Q2
m 1
23526,36
3 1
11763,18
S х22
m k
Q3 n ( x ij x i x j x) 2
i 1 j 1
.
10 [(906,57 - 969,71 - 940,64 1002,48 ) 2
(939,97 - 1001,624 - 940,64 1002,48 ) 2
При
взаимодействи
и между
факторами
(975,39 - 1036,097 - 940,64 1002,48 ) 2
(966,93 - 969,71 - 1000,94 1002,48 )
S х21х 2
2
(1000,60 - 1001,62 - 1000,94 1002,48 ) 2
(1035,28 - 1036,1 - 1000,94 1002,48 ) 2
f 3 (k 1)
(m 1) 4
(1035,63 - 969,7103 - 1065,85 1002,48 ) 2
Q3
(k 1) (m 1)
157,42
39,35
4
(1064,30 - 1001,62 - 1065,85 1002,48 ) 2
(1097,63 - 1036,1 - 1065,85 1002,48 ) 2 ]
157,42
m k n
Q4 ( xij x ij ) 2
Внутри партии
(остаточная)
i 1 j 1 1
m k
(n 1) S ij2
i 1 j 1
f 4 k m (n 1)
3 3 9 81
Q4
k m(n 1)
3718,98
45,91
S n2
44.
Проверка взаимодействия междуфакторами х1 и х2
Проверка гипотезы об отсутствии взаимодействия
между исследуемыми факторами – вычисляем
дисперсионное соотношение
F
S n2
2
/ S AБ
45,91 / 39,35 1,17
Принимаем
таблице
по
f1 f 3
f2 f4
f 3 (k 1) (m 1)
f 4 k m(n 1)
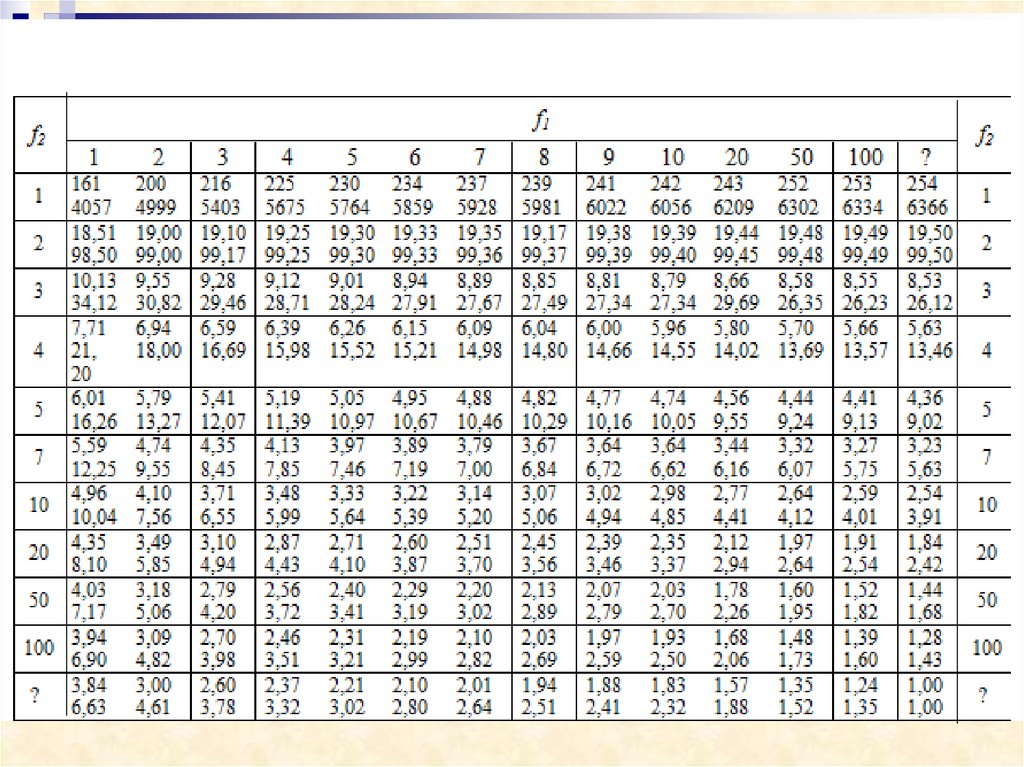
При f1=81 и f2=4 F0,05= 5,634.
Расчетное
значение F существенно меньше табличного
значения,
что
подтверждает
гипотезу
об
отсутствии взаимодействия между исследуемыми
факторами.
45.
46.
Проверяем значимость влияния обоихфакторов на исследуемую величину Y.
Вычисляем общую оценку дисперсий
S 02 (Q3 Q4 ) /( f 3 f 4 ) (157,42 3718,98) /( 4 81) 45,6.
Вычисляем дисперсионные соотношения
F1 S х21 / S 02 3307,029 / 45,6 72,522;
и
F2 S х22 / S 02 11763,18 / 45,6 257,964.
При f1=k -1=2 и f2=f3+f4= 85 F0,05=3,15, F1 и F2
на много больше табличных значений.
Из результатов расчета следует, что исследуемые
факторы х1 и х2 оказывают сильное влияние на
случайную величину Y.
47.
Так как влияние обоих факторовзначимо, то мы имеем дело с k*m = 9
нормально распределенными
генеральными совокупностями с общей
2
дисперсией и разными значениями
а ij , оценками которых служат
выборочная дисперсия S20 и
выборочные средние yij для каждой
комбинации факторов
48. Определение параметров выборок
Интервальные, оценки среднеквадратического отклоненияи математического ожидания выборок определяют по
формулам
f3 f 4
S0 Z 2
f3 f 4 1
S0 Z1
S 0 t , f
n
Z1
f3 f 4
,
f3 f 4 1
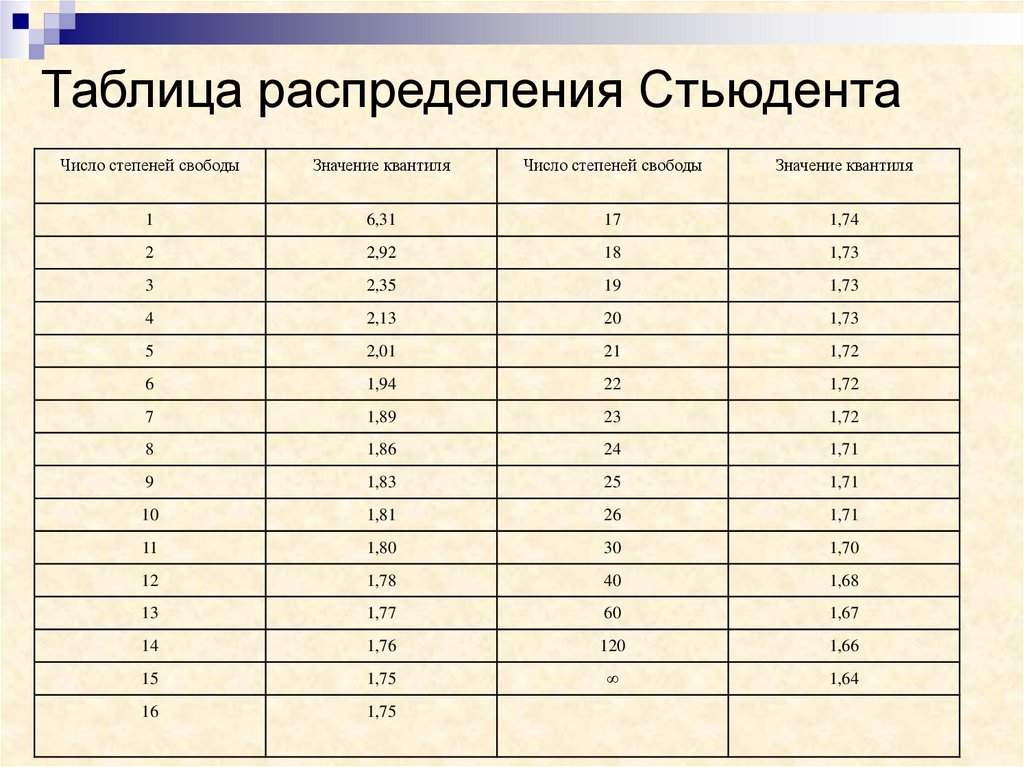
45,6 1,665
3,56.
10
xij
S0 t , f
n
aij xij
f f 3 f 4 4 81 85
f3 f 4
4 81
0,85
0,845;
f3 f 4 1
4 81 1
Z2
S0 t , f
n
;
t , f 1,665
f3 f 4
4 81
1,2
1,193.
f3 f 4 1
4 81 1
Значения Z1 и Z2 находим по табл. при принятой доверительной вероятности
γ=0,95 и количестве наблюдений n= f f 3 f 4
49.
Таблица распределения СтьюдентаЧисло степеней свободы
Значение квантиля
Число степеней свободы
Значение квантиля
1
6,31
17
1,74
2
2,92
18
1,73
3
2,35
19
1,73
4
2,13
20
1,73
5
2,01
21
1,72
6
1,94
22
1,72
7
1,89
23
1,72
8
1,86
24
1,71
9
1,83
25
1,71
10
1,81
26
1,71
11
1,80
30
1,70
12
1,78
40
1,68
13
1,77
60
1,67
14
1,76
120
1,66
15
1,75
∞
1,64
16
1,75
50.
Число степенейсвободы
Z1
Z2
2
0,446
31,623
3
0,521
6,287
4
0,566
3,727
5
0,599
2,875
6
0,624
2,453
7
0,644
2,202
8
0,661
2,035
9
0,675
1,916
10
0,688
1,826
20
0,76
1,460
50
0,835
1,246
100
0,878
1,162
200
0,911
1,109
51.
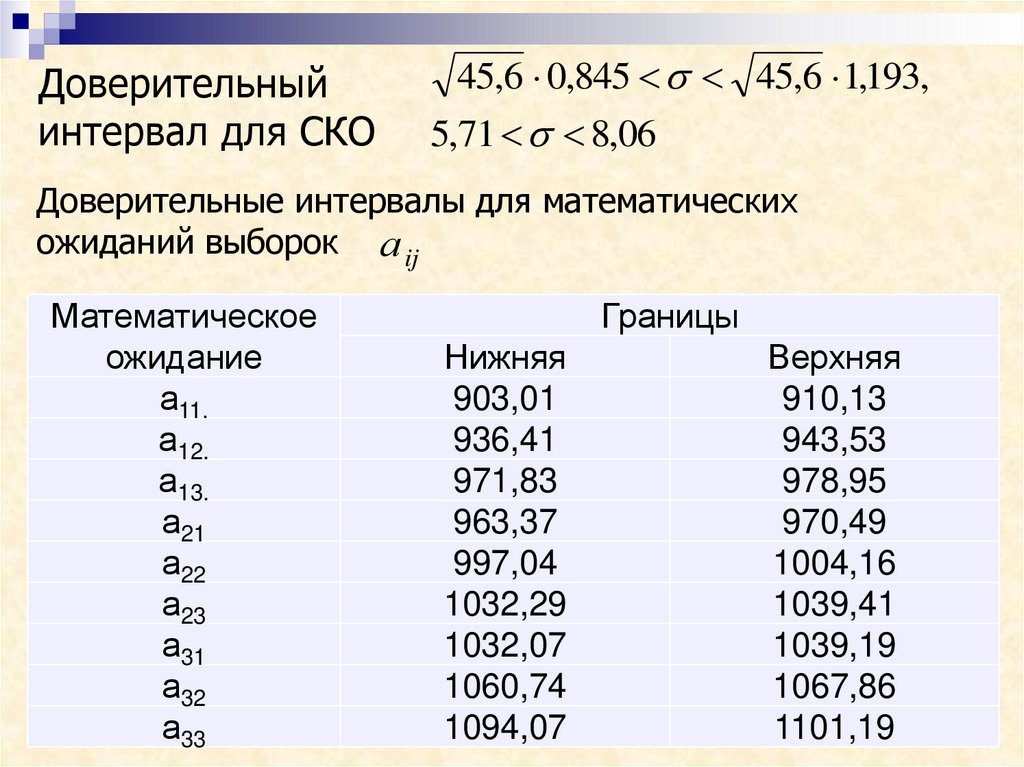
Доверительныйинтервал для СКО
45,6 0,845 45,6 1,193,
5,71 8,06
Доверительные интервалы для математических
ожиданий выборок а ij
Математическое
ожидание
а11.
а12.
а13.
а21
а22
а23
а31
а32
а33
Границы
Нижняя
903,01
936,41
971,83
963,37
997,04
1032,29
1032,07
1060,74
1094,07
Верхняя
910,13
943,53
978,95
970,49
1004,16
1039,41
1039,19
1067,86
1101,19










































 Математика
Математика








