Похожие презентации:
Определение натуральной величины. Лекция
1.
ЛЕКЦИЯ. ОПРЕДЕЛЕНИЕНАТУРАЛЬНОЙ
ВЕЛИЧИНЫ
2.
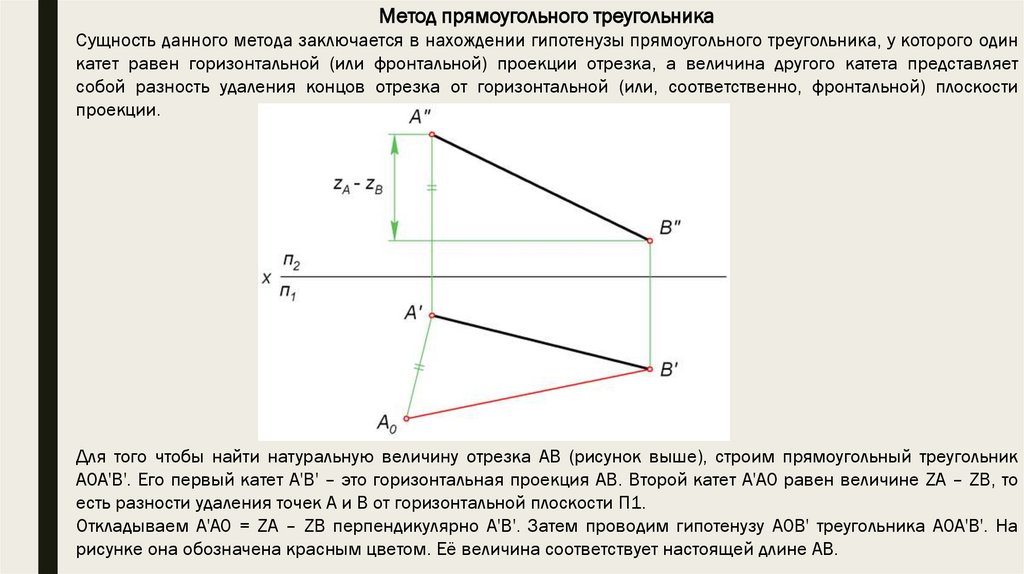
Метод прямоугольного треугольникаСущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один
катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет
собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости
проекции.
Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник
A0A'B'. Его первый катет A'B' – это горизонтальная проекция AB. Второй катет A'A0 равен величине ZA – ZB, то
есть разности удаления точек A и B от горизонтальной плоскости П1.
Откладываем A'A0 = ZA – ZB перпендикулярно A'B'. Затем проводим гипотенузу A0B' треугольника A0A'B'. На
рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.
3.
Способ параллельного переносаПараллельный перенос представляет собой перемещение геометрической фигуры параллельно
одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется.
Например, если перемещать отрезок EF параллельно горизонтальной плоскости П1, то длина его
проекции E'F' не изменится, когда она займет новое положение E'1F'1 (как это показано на рисунке
ниже).
Еще одно важное свойство параллельного переноса заключается в том, что при любом
перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция
движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной
плоскости, то её горизонтальная проекция движется по прямой, параллельной оси Y.
4.
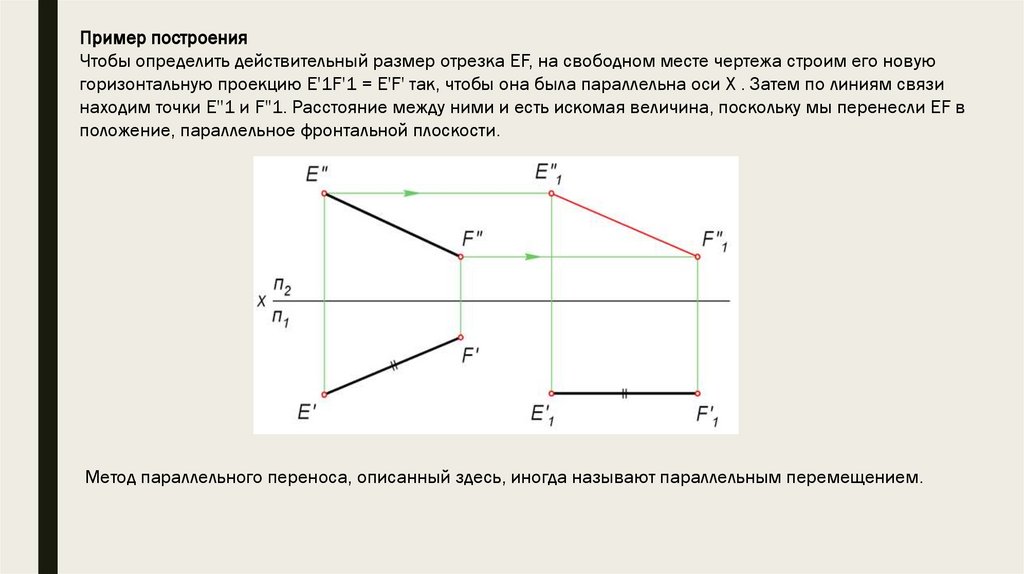
Пример построенияЧтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую
горизонтальную проекцию E'1F'1 = E'F' так, чтобы она была параллельна оси X . Затем по линиям связи
находим точки E''1 и F''1. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в
положение, параллельное фронтальной плоскости.
Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением.
5.
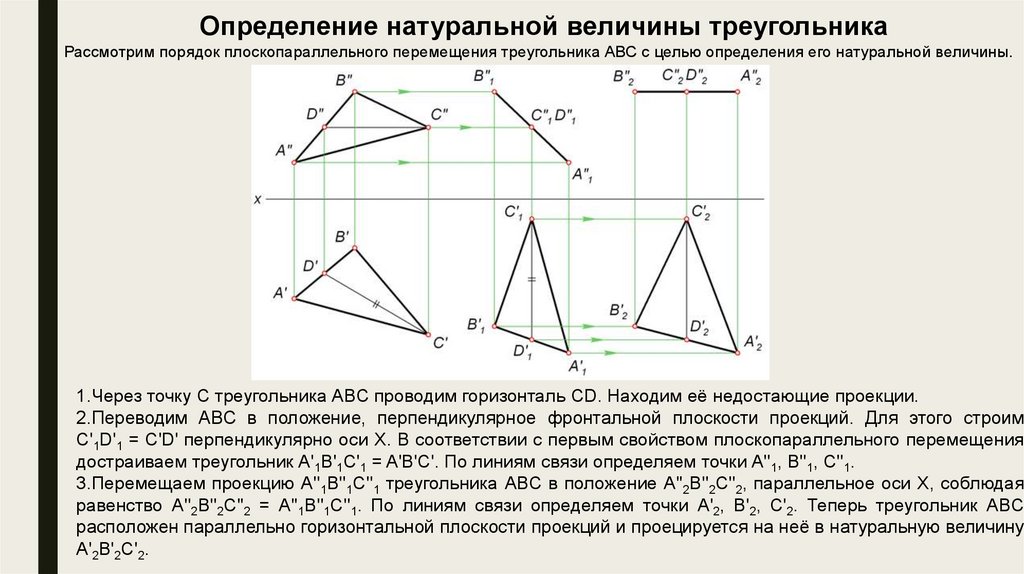
Определение натуральной величины треугольникаРассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.
1.Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2.Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим
C'1D'1 = C'D' перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения
достраиваем треугольник A'1B'1C'1 = A'B'C'. По линиям связи определяем точки A''1, B''1, C''1.
3.Перемещаем проекцию A''1B''1C''1 треугольника ABC в положение A''2B''2C''2, параллельное оси X, соблюдая
равенство A''2B''2C''2 = A''1B''1C''1. По линиям связи определяем точки A'2, B'2, C'2. Теперь треугольник ABC
расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину
A'2B'2C'2.
6.
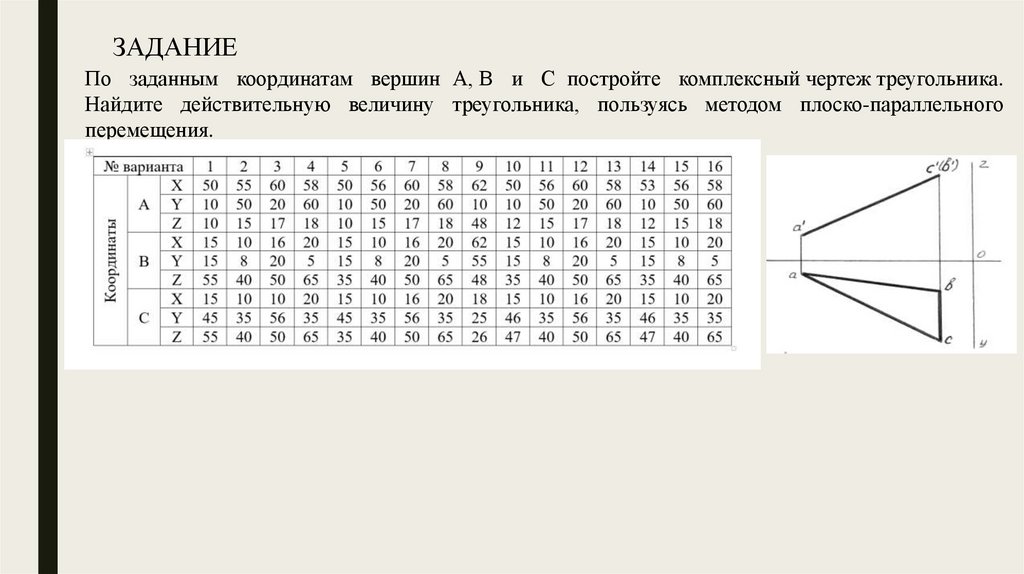
ЗАДАНИЕПо заданным координатам вершин А, В и С постройте комплексный чертеж треугольника.
Найдите действительную величину треугольника, пользуясь методом плоско-параллельного
перемещения.


 Инженерная графика
Инженерная графика








