Лекция 4

1.

НЕРАВНОВЕСНАЯ
ТЕРМОДИНАМИКА. ТЕОРИЯ
ОНЗАГЕРА

2.

НЕРАВНОВЕСНАЯ
ТЕРМОДИНАМИКА. ТЕОРИЯ
ОНЗАГЕРА
1903 - 1976 гг)
Ларс Онзагер опубликовал свою работу в двух статьях в
«Physical Review» в 1931 году, и когда он ее представил в
1933 году в Норвежский технологический институт в
Тронхейме в качестве докторской диссертации, то она
была признана неприемлемой. Теория Онзагера была
понята и оценена научным сообществом только в конце
40-х годов прошлого столетия, а в формулировке его
Нобелевской премии по химии 1968 года было написано: «за
открытие соотношений взаимности, носящих его имя,
фундаментальных для термодинамики необратимых
процессов»

3.

НЕРАВНОВЕСНАЯ
ТЕРМОДИНАМИКА. ТЕОРИЯ
ОНЗАГЕРА
Принцип локального равновесия.
Скорости производства энтропии и диссипации энергии.
Соотношение Теодора де Донде
Кинетические коэффициенты Онзагера и соотношение взаимности.
Принцип симметрии Кюри.
Формула Курзона и Альборна.
Термоэлектрические явления. Эффекты Зеебека, Пельтье и Томсона.
Термодиффузионные кинетические явления. Эффекты Дюфура и Соре.

4.

ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ.

5.

ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ.
Использование таких понятий как температура, энтропия,
давление и пр. для описания неравновесных процессов
возможно и основывается на принципе локального
равновесия, суть которого состоит в том, что значение
любой из перечисленных выше термодинамических величин
следует определять не глобально для всей неравновесной
системе в целом, а локально, т.е. путём задания их
локальных значений, относящихся к физически малому
объёму системы.

6.

ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ.
Использование таких понятий как температура, энтропия,
давление и пр. для описания неравновесных процессов
возможно и основывается на принципе локального
равновесия, суть которого состоит в том, что значение
любой из перечисленных выше термодинамических величин
следует определять не глобально для всей неравновесной
системе в целом, а локально, т.е. путём задания их
локальных значений, относящихся к физически малому объёму
системы. Таким образом, несмотря на то, что вся система
находится в неравновесном состоянии, каждая малая часть
системы может при этом находиться в равновесном
состоянии и, следовательно, может характеризоваться
локальными значениями температуры, давления,
химического потенциала.

7.

ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ.
Использование таких понятий как температура, энтропия,
давление и пр. для описания неравновесных процессов
возможно и основывается на принципе локального
равновесия, суть которого состоит в том, что значение
любой из перечисленных выше термодинамических величин
следует определять не глобально для всей неравновесной
системе в целом, а локально, т.е. путём задания их
локальных значений, относящихся к физически малому объёму
системы. Таким образом, несмотря на то, что вся система
находится в неравновесном состоянии, каждая малая часть
системы может при этом находиться в равновесном
состоянии и, следовательно, может характеризоваться
локальными значениями температуры, давления, химического
потенциала. Другими словами, установление полного
равновесия термодинамической системы является
процессом иерархическим как по времени, так и по
пространственному масштабу.

8.

dE Q W dN TdS PdV Z n dX n l dNl
n
l

9.

dE Q W dN TdS PdV Z n dX n l dN l
n
dE Q W Td e S P dV Z n dX n
n
l

10.

dE Q W dN TdS PdV Z n dX n l dNl
n
dE Q W Td e S P dV Z n dX n
n
dE T (d e S di S ) P dV ( P P )dV
l

11.

dE Q W dN TdS PdV Z n dX n l dNl
n
dE Q W Td e S P dV Z n dX n
n
dE T (d e S di S ) P dV ( P P )dV
dE T (d e S di S ) PdV
l

12.

dE Q W dN TdS PdV Z n dX n l dNl
n
l
dE T (de S di S ) PdV Z n dX n l dNl
diS
i Q
n
l
1
P
Z
dQ dV dX dN 0
T
T
T
T
T
Z
Z
Y
d i S n dX n Yn dX n 0
T
n
n
T

13.

dE Q W dN TdS PdV Z n dX n l dNl
n
l
dE T (de S di S ) PdV Z n dX n l dNl
diS
i Q
n
l
1
P
Z
dQ dV dX dN 0
T
T
T
T
T
Z
Z
Y
d i S n dX n Yn dX n 0
T
n
n
T

14.

dE Q W dN TdS PdV Z n dX n l dNl
n
l
dE T (de S di S ) PdV Z n dX n l dNl
diS
i Q
n
l
1
P
Z
dQ dV dX dN 0
T
T
T
T
T
Z
Z
Y
d i S n dX n Yn dX n 0
T
n
n
T
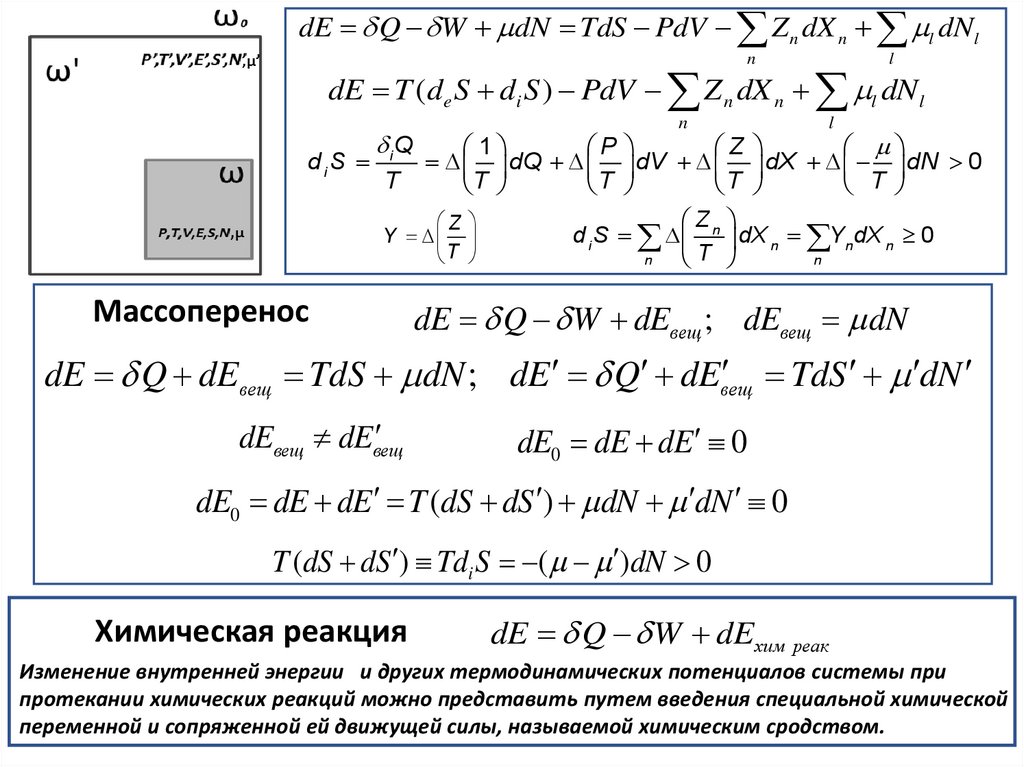
Массоперенос
dE Q W dEвещ ; dEвещ dN
TdS dN
dE Q dEвещ TdS dN ; dE Q dEвещ
dEвещ dEвещ
dE0 dE dE 0
dE0 dE dE T (dS dS ) dN dN 0
T (dS dS ) Tdi S ( )dN 0

15.

dE Q W dN TdS PdV Z n dX n l dNl
n
l
dE T (de S di S ) PdV Z n dX n l dNl
diS
i Q
n
l
1
P
Z
dQ dV dX dN 0
T
T
T
T
T
Z
Z
Y
d i S n dX n Yn dX n 0
T
n
n
T
Массоперенос
dE Q W dEвещ ; dEвещ dN
TdS dN
dE Q dEвещ TdS dN ; dE Q dEвещ
dEвещ dEвещ
dE0 dE dE 0
dE0 dE dE T (dS dS ) dN dN 0
T (dS dS ) Tdi S ( )dN 0
Химическая реакция
dE Q W dEхим реак
Изменение внутренней энергии и других термодинамических потенциалов системы при
протекании химических реакций можно представить путем введения специальной химической
переменной и сопряженной ей движущей силы, называемой химическим сродством.

16.

17.

ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ.
Математически это означает, что вместо глобальных интенсивных параметров,
относящихся ко всей системе в целом, вводятся термодинамические переменные в виде
функций координат и времени
T T x , t , P P x , t , x, t ,
а экстенсивные параметры – энергия, энтропия, число частиц, заменяются их локальными
плотностями, отнесенными к единице объема, которые тоже рассматриваются как
функции координат и времени: s ( x, t ) – плотность энтропии, u ( x , t ) – плотность энергии,
( x , t ) – плотность вещества и т.д. Полные значения экстенсивных параметров,
относящиеся ко всей системе в целом, находятся путем интегрирования функций плотности
этих величин по всему объему системы.

18.

ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ.
Понятие физически малого объёма, по отношению к которому определяют локальные
значения термодинамических параметров, понимается таким образом, что физически
малый объём все же можно рассматривать как макроскопическую систему, содержащую
большое число молекул, характерный размер которой намного больше среднего
межмолекулярного расстояния. Например, достаточно большое число молекул, порядка
1010 в жидкости занимает достаточно малый объём, порядка 10-12см3, а в газе при
нормальных стандартных условиях порядка 10-9 см3. Таким образом, при масштабе
размеров физически малого объёма порядка 10-3-10-4 см, относительная дисперсия
различных термодинамических параметров будет составлять величину порядка 10-5.

19.

ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ.
Время установления локального равновесия в газе можно оценить исходя из
частоты столкновений отдельной молекулы с другими такими же частицами
f ~ uT
(7.3)
где uT – средняя тепловая скорость молекулы, – площадь ее сечения, – плотность
газа. Подставляя в формулу (7.3) характерные значения uT ~ 105 см / с ,
~ 1019 см 3 , ~ 10 15 см2 и считая, что для установления максвелловского распределения
по скоростям достаточно десятка столкновений одной молекулы с окружением, получим
оценку времени установления локального равновесия ~ 0,1 f 1 ~ 10 8 с . Для
конденсированного состояния вещества с учетом того, что плотность ~ 1022 см 3 , такая
оценка дает величину ~ 10 11 с . Таким образом, принцип локального равновесия
является достаточно хорошим приближением для рассмотрения неравновесных
процессов, если считать, что методы классической равновесной термодинамики
применимы локально, т.е. выполняются в физически малых объемах вещества

20.

СКОРОСТИ ПРОИЗВОДСТВА ЭНТРОПИИ И ДИССИПАЦИИ ЭНЕРГИИ.
Для характеристики неравновесного процесса вводят локальную скорость
производства энтропии в единице объема и локальную скорость диссипации
энергии:
1 dS
i
V dt
1 iQ
V dt
T

21.

СКОРОСТИ ПРОИЗВОДСТВА ЭНТРОПИИ И ДИССИПАЦИИ ЭНЕРГИИ.
Для характеристики неравновесного процесса вводят локальную скорость
производства энтропии в единице объема и локальную скорость диссипации
энергии:
1 dS
i
V dt
1 iQ
V dt
T
Если состояние системы определяется несколькими обобщенными координатами
X 1 , ... , X n и сопряженными им обобщенными термодинамическими силами Z1 , ... , Z n ,
то работа, совершаемая в равновесном процессе, будет равна Wmax
потерянная работа неравновесного процесса:
Z dX , а
Wlost i Q Z k dX k
k
k
k
Здесь Z k обозначает разницу между значениями термодинамической силы в самой
системе и во внешней среде.

22.

СКОРОСТИ ПРОИЗВОДСТВА ЭНТРОПИИ И ДИССИПАЦИИ ЭНЕРГИИ.
Для характеристики неравновесного процесса вводят локальную скорость
производства энтропии в единице объема и локальную скорость диссипации
энергии:
1 dS
i
V dt
1 iQ
V dt
T
Если состояние системы определяется несколькими обобщенными координатами
X 1 , ... , X n и сопряженными им обобщенными термодинамическими силами Z1 , ... , Z n ,
то работа, совершаемая в равновесном процессе, будет равна Wmax
потерянная работа неравновесного процесса:
Z dX , а
Wlost i Q Z k dX k
k
k
k
Здесь Z k обозначает разницу между значениями термодинамической силы в самой
системе и во внешней среде.
Соотношение Теодора де Донде
Zk
J k Yk J k 0
T
k
k
Jk
1 dX k
V dt
Zk
Yk
T
плотность потока обобщенной координаты
движущая сила термодинамического процесса, которую можно
также называть сродством данного процесса (по аналогии с
химическим сродством )

23.

КИНЕТИЧЕСКИЕ КОЭФФИЦИЕНТЫ ОНЗАГЕРА И СООТНОШЕНИЕ ВЗАИМНОСТИ
Поток данной обобщённой координаты есть функция всех обобщенных сил:
J k J k Y1 ,...Yn
J k
2 Jk
J k J k (0)
Y j
YlY j ... LkiYi
j Y j
j
l Yl Y j
i
J k
Lkj - кинетические коэффициенты Онзагера
Y j
1 di S
J k Yk Yk LkjY j LkjYk Y j 0
V dt
k
k
j
k, j
( L12 L21 ) 4 L11 L22 ; L11 0; L22 0
2
Ключевым положением теории Онзагера является соотношение взаимности для
перекрестных кинетических коэффициентов:
Lkj L jk