Похожие презентации:
Основные понятия дифференциальных уравнений
1.
ЛЕКЦИЯ 15. Основные понятиядифференциальных
уравнений
2. Учебные вопросы
1. Введение в теорию ДУ:задачи, приводящие к понятию
дифференциального уравнения.
2.Обыкновенные
дифференциальные уравнения,
основные понятия (порядок,
степень, решение).
3.Дифференциальные уравнения
первого порядка.
3.
4. Частное и общее решения,интегральные кривые, поле
направлений.
5. Интегрирование уравнений с
разделяющимися переменными.
4. 1.Задачи, приводящие к понятию дифференциального уравнения.
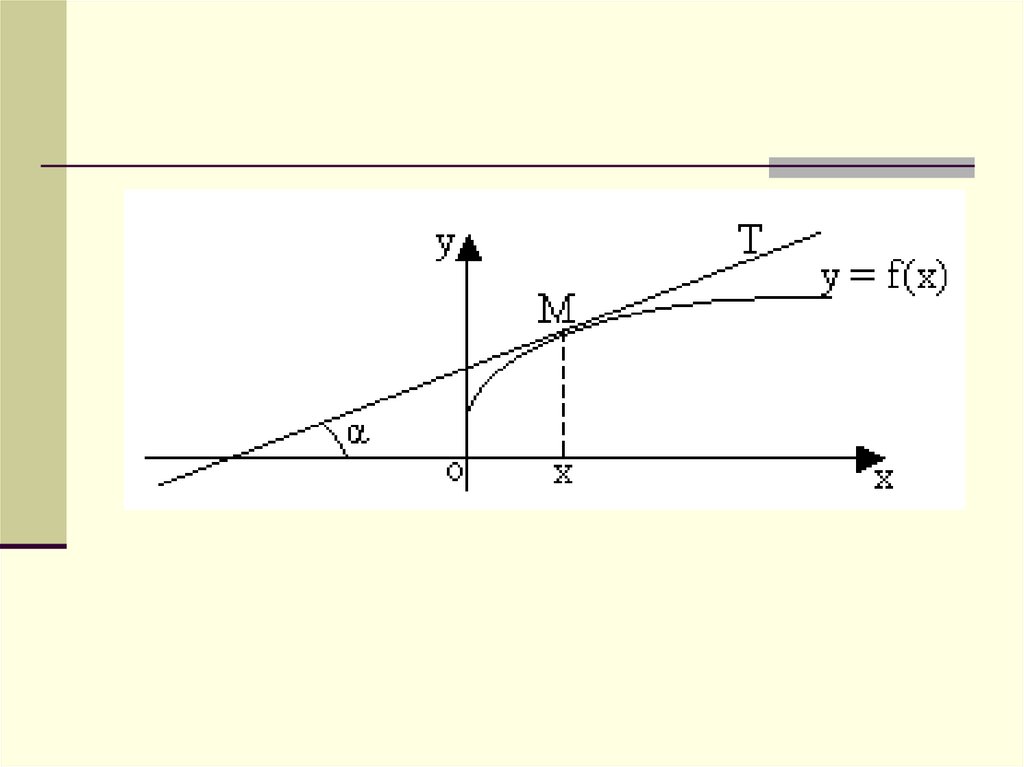
Задача 1.На плоскости XOY найти кривую,
которая в каждой своей точке имеет
касательную, образующую с
положительным направлением оси Ox
угол, тангенс которого равен
удвоенной абсциссе точки касания.
Решение.
Пусть уравнение искомой кривой y=f(x).
5.
6.
Угловой коэффициент касательной МТесть tgα, он равен производной от y по
x, так что
tg y
С другой стороны, по условию задачи
имеем
tg 2 x .
Приравнивая значения tg α, получим
y 2 x
7.
Решением дифференциальногоуравнения является любая
первообразная для функции 2x.
Например,
2
решением будет y x .
8.
Все первообразные для функции2x и, следовательно, все решения
дифференциального уравнения
задаются формулой
2
y x C .
9.
Дифференциальное уравнениеимеет бесчисленное множество
решений.
10.
Но если в условие задачидобавить точку M0 (x0, y0),
через которую проходит
искомая кривая, то получим
единственную кривую.
11.
Для этого достаточно заменить вуравнении координаты x и y
координатами точки M0
y0 x0 C0
2
12.
Отсюда имеем C0 y0 x0 и2
y x x y0
2
2
0
Таким образом, искомой кривой
будет парабола.
13. Задача 2.
Допустим, что в каждый моментвремени t известна скорость v(t)
точки, движущейся по оси OX, где
v(t) - функция, непрерывная на
(a,b).
14.
Кроме того, известно значение х0положения точки в определенный
момент времени t0 . Требуется
найти закон движения точки.
15. Решение.
Положение точки определяетсяодной координатой х и задача
состоит в том, чтобы выразить х
как функцию от t . Принимая во
внимание механический смысл
первой производной, мы получим
равенство
dx
dt
v(t )
16.
Как известно из интегральногоисчисления
t
x(t ) v(t )dt C , (a t b)
t0
17.
Так как в формулу входитпроизвольная постоянная C, то
мы ещё не получили определённого
закона движения точки.
18.
Поскольку движущаяся точкапринимает положение х0 в
заданный момент времени t0, то
t
x0 v(t )dt C , С х0
t0
19.
Итак, закон движения точкиимеет вид
t
.
x(t ) v(t )dt х0 , (a t b)
t0
20. Учебный вопрос.
Обыкновенныедифференциальные уравнения,
основные понятия (порядок,
степень, решение).
21. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, ОСНОВНЫЕ ПОНЯТИЯ.
Определение. Обыкновеннымдифференциальным уравнением n–ого
порядка называется выражение вида:
F x, y, y , y , ... , y
n
0,
где х – независимая переменная;
у(х) – неизвестная функция;
n
y , y ,..., y
– производные искомой
функции.
22.
Определение. Порядком n дифферен-циального уравнения называется
порядок наивысшей производной,
входящей в это уравнение.
Например,
y
(5)
y y 0
2 x y e y 1 0
2
x
23.
Определение. Решениемдифференциального уравнения
называется функция у=φ(х),
которая при подстановке в
уравнение обращает его в верное
равенство.
24.
Определение. График решениядифференциального уравнения
называется интегральной кривой
дифференциального уравнения.
Процесс нахождения решения
дифференциального уравнения
называется интегрированием этого
уравнения.
25.
Определение. Решениедифференциального уравнения,
полученное в неявном виде
,
называется интегралом
дифференциального уравнения.
( x, y ) 0
26. Учебный вопрос.
Дифференциальные уравненияпервого порядка.
27. Дифференциальные уравнения первого порядка.
Определение. Дифференциальнымуравнением первого порядка
называется соотношение,
связывающее независимую
переменную, искомую функцию и
ее первую производную:
,F ( x, y , y ) 0
dy
где
у
dx
28.
Если уравнениеF ( x, y, y ) 0
разрешить относительно
производной , то получим
уравнение нормального вида:
y f ( x, y ).
29. Учебный вопрос.
ЧАСТНОЕ И ОБЩЕЕРЕШЕНИЯ,
ИНТЕГРАЛЬНЫЕ
КРИВЫЕ, ПОЛЕ
НАПРАВЛЕНИЙ
30. ЧАСТНОЕ И ОБЩЕЕ РЕШЕНИЯ, ИНТЕГРАЛЬНЫЕ КРИВЫЕ, ПОЛЕ НАПРАВЛЕНИЙ
Определение. Решение у=φ(х,С),которое зависит от независимой
переменной х и произвольной
постоянной, называется общим
решением ДУ первого порядка.
31.
Решение у=φ(х), полученное изобщего при фиксированном
значении произвольной
постоянной, называется частным
решением ДУ первого порядка.
32.
Задача Коши для уравненияF ( x, y, y ) 0
состоит в том, чтобы найти
частное решение уравнения,
удовлетворяющее начальному
условию
y ( x0 ) y0
33.
УравнениеF ( x, y , y ) 0
в каждой точке
M (x , y) области, где определено
его решение у=φ(х ,С ),
задаёт направление касательной к
интегральной кривой. В итоге мы
получаем целое поле
направлений.
34.
Это поле графически можноизобразить, поместив в каждой
точке M(x, y) черточку,
наклоненную к оси Ox под углом,
тангенс которого равен
tg y
35.
36. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Определение. ДУ первого порядканазывается уравнением с
разделенными переменными, если
его можно представить в виде
f x dx g y dy 0
37.
Решение этого уравненияf ( x)dx g ( y )dy,
f
(
x
)
dx
g
(
y
)
dy
,
F ( x ) G ( y ) C ,
F ( x) G ( y ) C
38.
Пример. Найти общее решениедифференциального уравнения
dy
2 xdx
0
y
Решение.
39.
dy2 xdx ,
y
dy
2 xdx y ,
2
x ln y C ,
2
ln y C x ,
C x2
y e
,
c
x2
х2
y e e или у Се
40.
Определение. Уравнение видаP( x) Q( y) dx R( x) S ( y) dy 0
называется уравнением с
разделяющимися переменными.
R( x) Q( y) 0
41.
В этом уравнении легко разделитьпеременные. Для этого поделим
уравнение на произведение
R( x) Q( y) 0 . Тогда получим
P( x)
S ( y)
dx
dy 0
R( x)
Q( y )
- это уравнение с разделенными
переменными.
42.
Общим интегралом будетP( x)
S ( y)
dx
dy С
R( x)
Q( y )
43. ЗАМЕЧАНИЕ
Мы могли потерять некоторыерешения, которые обращают в
нуль произведение R(x)Q(y), а
именно Q(y)=0, отсюда yk= ak ,где
ak – const.
44.
Если решения yk= ak получаютсяиз общего при подходящем
выборе С, то такие решения будут
частными, если же подобрать
нужное С невозможно, то они
называются особыми решения.
45. Пример.
Найти общий интеграл и частноерешение уравнения
x 1 y 2 dx y 1 x 2 dy 0
удовлетворяющее условию y x 1 0 .
Решение.
Делим на
1 x 2 1 y 2 0 ,
тогда
46.
x dx1 x
2
x dx
1 x 2
y dy
0
1 y
2
y dy
x dx
1 y 2
y dy
1 x 1 y
2
2
47.
1 x2 1 y2 C1 x 2 1 y 2 C -общий интеграл.
Подставим начальное условие и найдем С:
.
1 ( 1) 1 0 C0 C0 1
2
2
48.
Частное решение1 x 1 y 1
2
2
Особое решение
1 x . 1 y 0, 1 x 1, y 1,
2
2
так как
x 0 dx 1 1 x 0 0,0 0.
2
49. Учебные вопросы
6. Однородные и линейные уравнения 1порядка.
7. Уравнения Бернулли 1-го порядка.
8. Дифференциальные уравнения высших
порядков, начальные и граничные условия.
50. Учебный вопрос.
Однородные и линейныеуравнения 1 порядка.
51. Однородные уравнения 1-го порядка.
Определение. Дифференциальеное уравнение 1порядка называется однородным ДУ-1,
если f(x,y) может быть представлена как
функция отношения своих аргументов,
т.е.
или
y
f ( x, y )
f ( x, y )
y
x
f(λx,λy)=f(x,y),
где λ – const.
52.
1) Однородные уравнения приводятся куравнениям с разделяющимися переменными
с помощью следующей замены: z y , т.е.
x
у=zх, отсюда у’=z’x+z .
2) После подстановки у, у’ в исходное
уравнение получим ДУ с разделяющимися
переменными, в котором неизвестной является
функция z(x).
y
3)После интегрирования в общем решении
необходимо z заменить на отношение x .
53. Пример
Решить уравнение ху+ y2 = (2х2 +ху)у’ .Решение.
54.
55.
56. Линейные уравнения первого порядка
Определение. Линейным дифференциальнымуравнением 1-го порядка называется уравнение
вида:
,
y p( x ) y q( x )
где у(х) – неизвестная функция.
Это уравнение линейно относительно у и у’ .
Если правая часть уравнения q(x) = 0, то
получим уравнение
y p( x ) y 0
,
которое называется линейным однородным,
соответствующим линейному неоднородному
уравнению.
57.
Рассмотрим линейное уравнение y p( x ) y q( x )Неизвестную функцию у(х) будем искать в
виде произведения неизвестных функций
у(х)=u(x)∙v(x), тогда y’=u’v+uv’. Подставляя
y и y’ в исходное уравнение, получим:
u v u v p( x ) u v q( x )
y
y
u v u v p( x )v q( x )
58.
Положим v p( x) v 0и найдем функцию v(x),решая это уравнение с разделяющи-мися
переменными:
dv ( x )
pv ( x )
dx
dv
p( x )dx
v
dv
p( x )dx
v
ln v p( x )dx
v e
p ( x ) dx
59.
Для нахождения u(x) подставим найденнуюфункцию v(x) и ее производную
p ( x ) dx
p ( x ) dx
v ( x ) e
e
p ( x )dx =
в уравнение, получим уравнение с
разделяющимися переменными
.
p ( x ) dx
u e
q( x)
Решим его
p( x ) e
p ( x ) dx
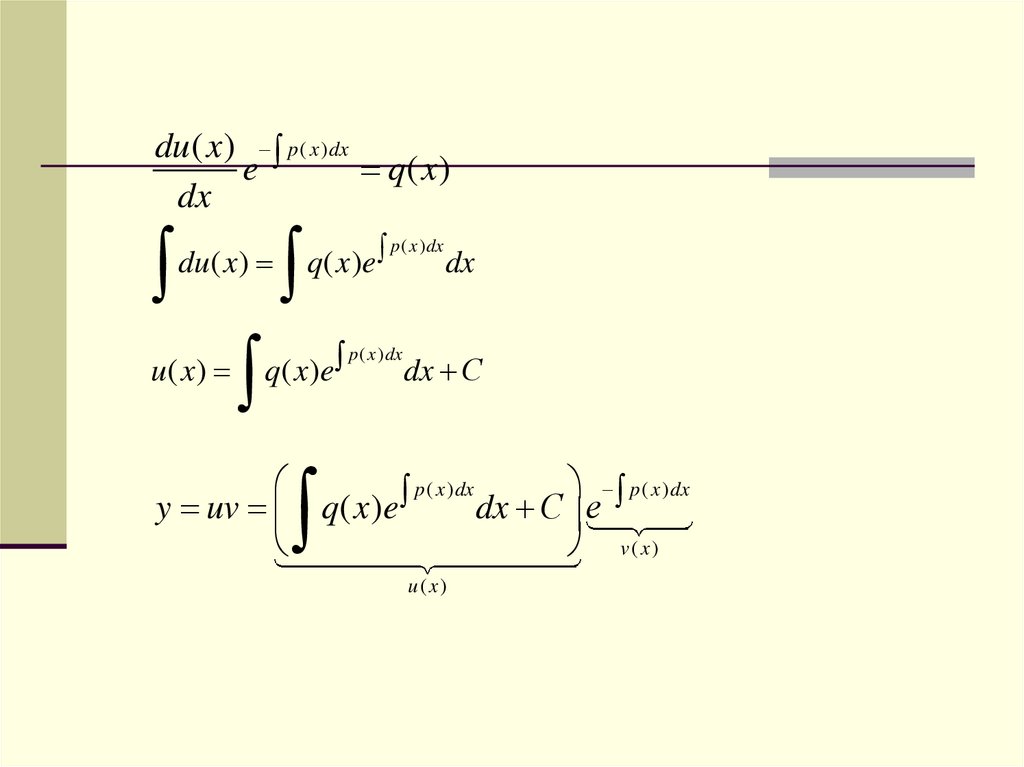
60.
du( x ) p ( x ) dxe
q( x )
dx
du( x )
u( x )
p ( x ) dx
q( x ) e
dx
p ( x ) dx
q( x ) e
dx С
p ( x ) dx
p ( x ) dx
y uv q( x )e
dx С e
v( x)
u( x)
61. Пример
Найти частное решение, удовлетворяющеезаданному начальному условию
3у
2
у
3 , у (1) 1
х
х
62.
63.
64.
Следовательно, частное решение данногодифференциального уравнения имеет вид:
у = 22 1.3
x
x
65. Учебный вопрос.
Уравнения Бернулли.66. Уравнения Бернулли.
Определение. Дифференциальноеуравнение вида dy P( x) y Q( x) y
,
dx
где α ≠ 0, 1
называется уравнением Бернулли.
1)Предполагая, что у ≠ 0, разделим
обе части уравнения Бернулли на уα.
В результате получим:
y
dy
P( x ) y 1 Q ( x )
dx
67.
2) Введем новую функцию z ( x) ( y( x)) 1 . Тогдаdz
dy
( 1) y
dx
dx уравнение на (-α+1) и перейдем в
3) Умножим
нем к функции z(x):
dz
( 1) Pz ( 1)Q
dx
68.
4)Получили линейное неоднородное уравнение1-го порядка. Это уравнение решается
методом множителей Бернулли.
5)Решив уравнение , подставим в его общее
решение вместо z(x) выражениеy 1 ,
получим общий интеграл уравнения Бернулли.
Уравнение Бернулли можно также решить,
не делая замены переменных, а сразу
применяя метод множителей Бернулли.
69. Пример
Найти общее решение уравненияРешение.
y xy ( x 1)e x y 2
70.
71.
Дифференциальныеуравнения высших порядков,
начальные и граничные
условия.
72. Дифференциальные уравнения высших порядков, начальные и граничные условия.
Определение. Уравнением n-го порядканазывается уравнение вида
n
f x, y, y , y ,..., y
0
, (n>1) .
Задача Коши уравнения n-го порядка ставится
следующим образом: найти решение y=y(x)
удовлетворяющее начальным условиям
y ( x0 ) y0 , y ( x0 ) y0 , y ( x0 ) y0 ,..., y ( n 1) ( x0 ) y0( n 1)
73.
Определение. Общим решением ДУ n-гопорядка называется функция
y=φ(x,C1,C2,…,Cn), которая при подстановке в
уравнение обращает его в верное равенство.





































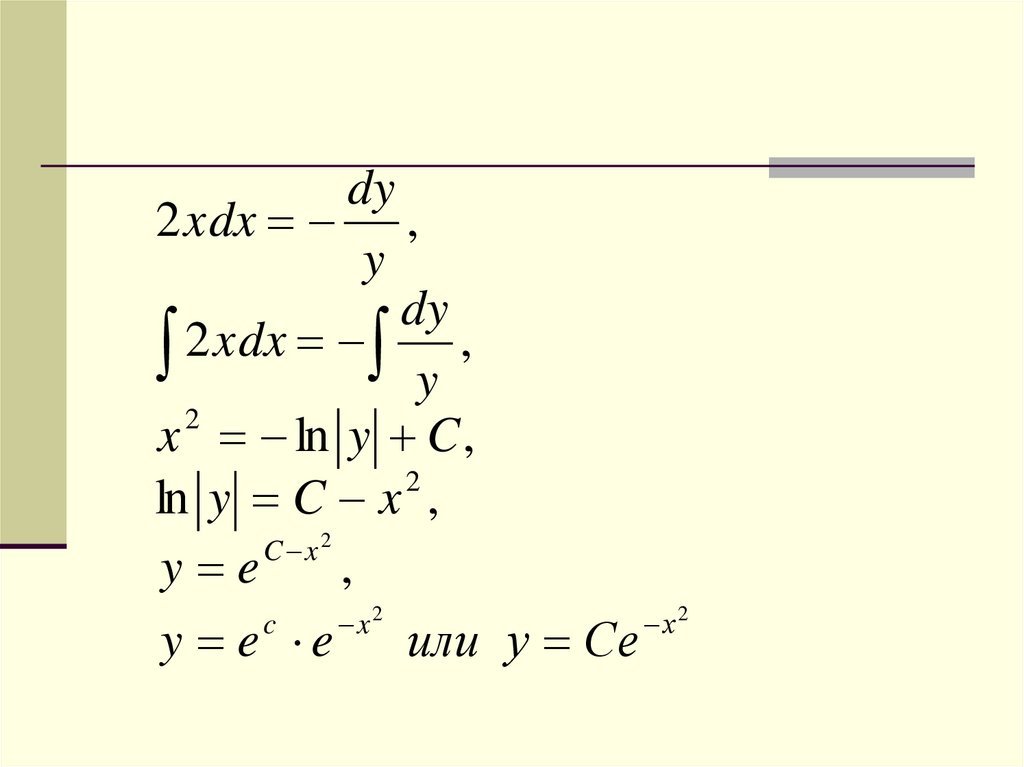






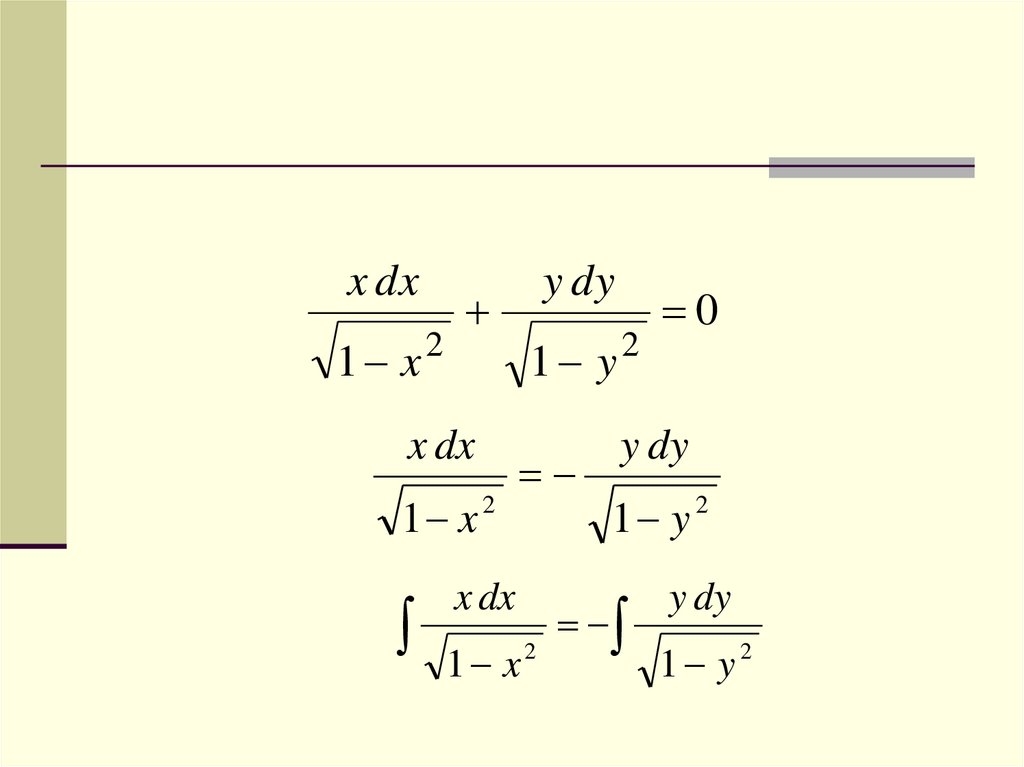


























 Математика
Математика








