Электромагнетизм МООК (1)

1.

Карагандинский технический университе им. А.Сагинова
Кафедра физики
Тема лекции:
Электромагнетизм.
1 часть
Для всех
специальностей
https://avatars.mds.yandex.net/get-imagescbir/2972862/UPS4fvrbocOxBHjoauPyhA8485/ocr
Лектор: к.х.н., старший преподаватель кафедры физики
Кусенова А.С.

2. План лекции

1. Магнитное поле в вакууме и его характеристики. Вектор
магнитной индукции.
2. Закон Био-Савара-Лапласа и его применение к расчету
полей.
3. Сила Ампера. Сила Лоренца.
4. Закон полного тока. Магнитный поток. Теорема Гаусса.
5. Работа по перемещению проводника с током в
магнитном поле.
6. Явление электромагнитной индукции. Закон Фарадея.
Вращение рамки в магнитном поле.
7. Индуктивность контура. Самоиндукция. Токи при
размыкании и замыкании цепи.
8. Взаимная индукция. Трансформаторы. Энергия магнитного поля.
9. Магнитные свойства вещества. Виды магнетиков.
10. Намагниченность. Магнитное поле в веществе.
11. Уравнения Максвелла для электромагнитного поля.

3. ОСНОВОПОЛОЖНИКИ ТЕОРИИ ЭЛЕКТРОМАГНЕТИЗМА

Андре Ампер
(1775-1836)
Майкл
Фарадей
(1791-1867)
https://avatars.mds.yandex.net/get-imagescbir/1532791/5pRw3uL5aIA91jGhOLgFgw7267/ocr
Джеймс
Максвелл
(1831-1879)
https://avatars.mds.yandex.net/get-imagescbir/4418486/6oZZZCk0Sk3QJ-YySm6nqg7357/ocr
Эмилий Ленц
(1804-1865)
https://avatars.mds.yandex.net/get-imagescbir/4480543/z5GSM0hoTJL3WL5tRoehDQ7488/ocr
https://avatars.mds.yandex.net/get-imagescbir/4009670/Whc9WWplTC2eR7CqoenoQA7557/ocr

4. Магнитное поле и его основные характеристики

Опыты показали, что подобно тому, как в
пространстве,
окружающем
неподвижные
электрические заряды, возникает электростатическое
поле, так и в пространстве, окружающем токи и
постоянные магниты, возникает силовое поле, которое
стало называться магнитным.
Особенности магнитного поля
магнитное поле создают движущиеся заряды ;
магнитное поле действует на движущиеся заряды;
магнитное
заряды.
поле НЕ действует на покоящиеся

5. Рамка с током.

При исследовании магнитного
поля пользуются замкнутым
плоским контуром с током
(рамка с током),
линейные размеры которого малы
по сравнению с расстоянием до
токов, образующих магнитное
поле. Ориентация контура в
пространстве
характеризуется
направлением нормали к контуру.
https://cf.pptonline.org/files/slide/k/k8nib937ErmloHgFXfCOLB4UsWQNevxh
2dDMZI/slide-7.jpg
Направление нормали задается правилом правого винта.

6. Направление магнитного поля.

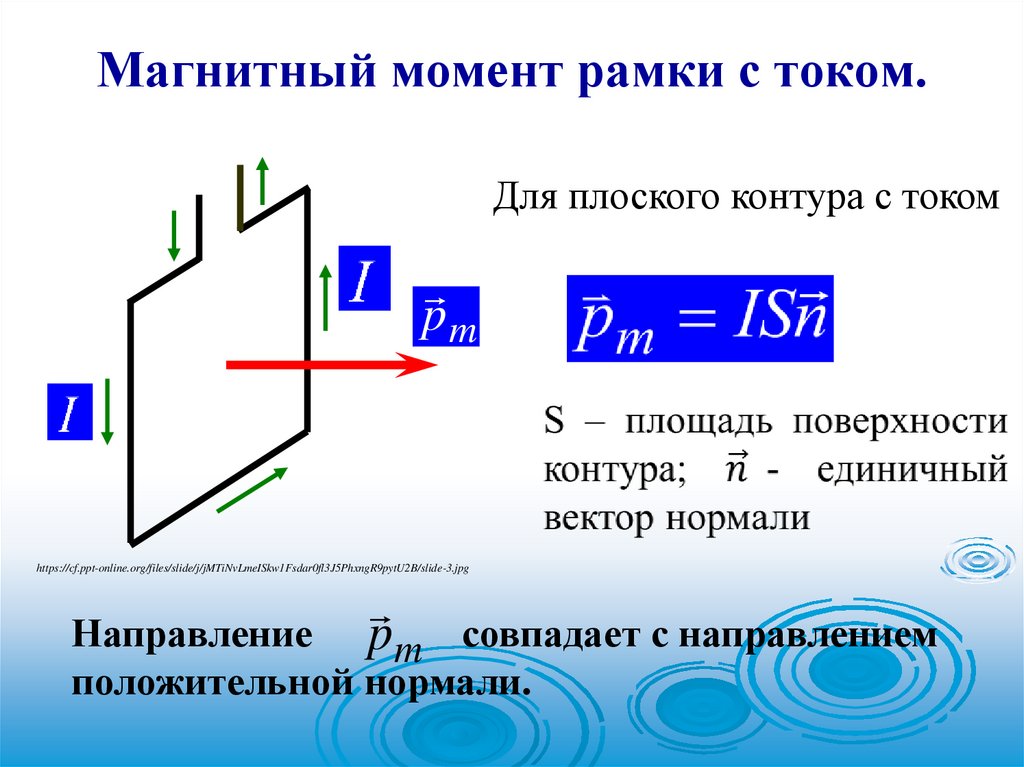
Магнитный момент рамки с током.
Для плоского контура с током
pm
https://cf.ppt-online.org/files/slide/j/jMTiNvLmeISkw1Fsdar0fl3J5PhxngR9pytU2B/slide-3.jpg
pm
Направление
совпадает с направлением
положительной нормали.

7. Магнитный момент рамки с током.

Вращающий момент сил.
На рамку с током в магнитном поле действует пара сил.
Вращающий момент сил
M
зависит от свойств поля в
данной точке и от свойств
B
F
рамки и определяется по
B формуле:
M
p
B
F
m
B
pm -вектор магнитного
pm
момента рамки с током.
B - вектор магнитной
https://s0.slide-share.ru/s_slide/14e395f48b8ad9de3b43fc73e89849e3/2a11661397ab-4b6e-8b62-e25399dc0d48.jpeg
индукции.
Вектор магнитного момента совпадает с направлением
положительной нормали к рамке.

8. Вращающий момент сил.

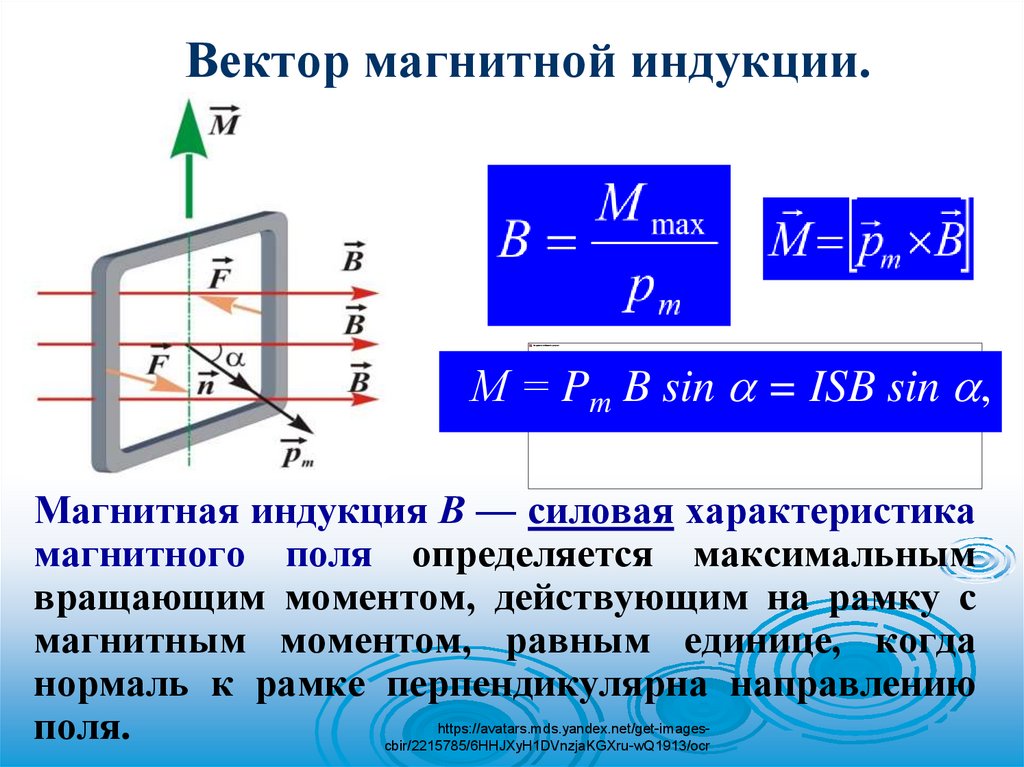
Вектор магнитной индукции.
М = Pm B sin = ISB sin ,
Магнитная индукция В — силовая характеристика
магнитного поля определяется максимальным
вращающим моментом, действующим на рамку с
магнитным моментом, равным единице, когда
нормаль к рамке перпендикулярна направлению
поля.
https://avatars.mds.yandex.net/get-imagescbir/2215785/6HHJXyH1DVnzjaKGXru-wQ1913/ocr

9. Вектор магнитной индукции.

Макротоки и микротоки
Различают
макроскопические токи электрические
токи,
протекающие
по
проводникам в электрических цепях и
микроскопические токи, обусловленных
движением электронов в атомах и молекулах.
Магнитное
поле макротока описывается
вектором напряженности магнитного поля Н.
Результирующее
магнитное
поле,
создаваемое всеми макро- и микротоками
характеризует вектор магнитной индукции В.

10. Макротоки и микротоки

Связь B и H.
Эта связь справедлива для однородной изотропной
среды.
B o H
o - магнитная постоянная, равная4 1 0 7 Г н / м
- безразмерная величина - магнитная
проницаемость среды, показывающая, во
сколько раз магнитное поле макротоков Н
усиливается за счет поля микротоков
среды.

11. Связь и .

Линии магнитной индукции.
Магнитное поле изображают с помощью линий
магнитной индукции.
Линии магнитной
индукции
это
линии,
I
касательные к которым в
каждой точке совпадают
с направлением вектора
B
В.
https://cf.ppt-online.org/files/slide/k/k8nib937ErmloHgFXfCOLB4UsWQNevxh2dDMZI/slide-9.jpg
Направление
линий
магнитной
индукции
определяется
правилом
правого
винта
(или
правилом буравчика).

12. Линии магнитной индукции.

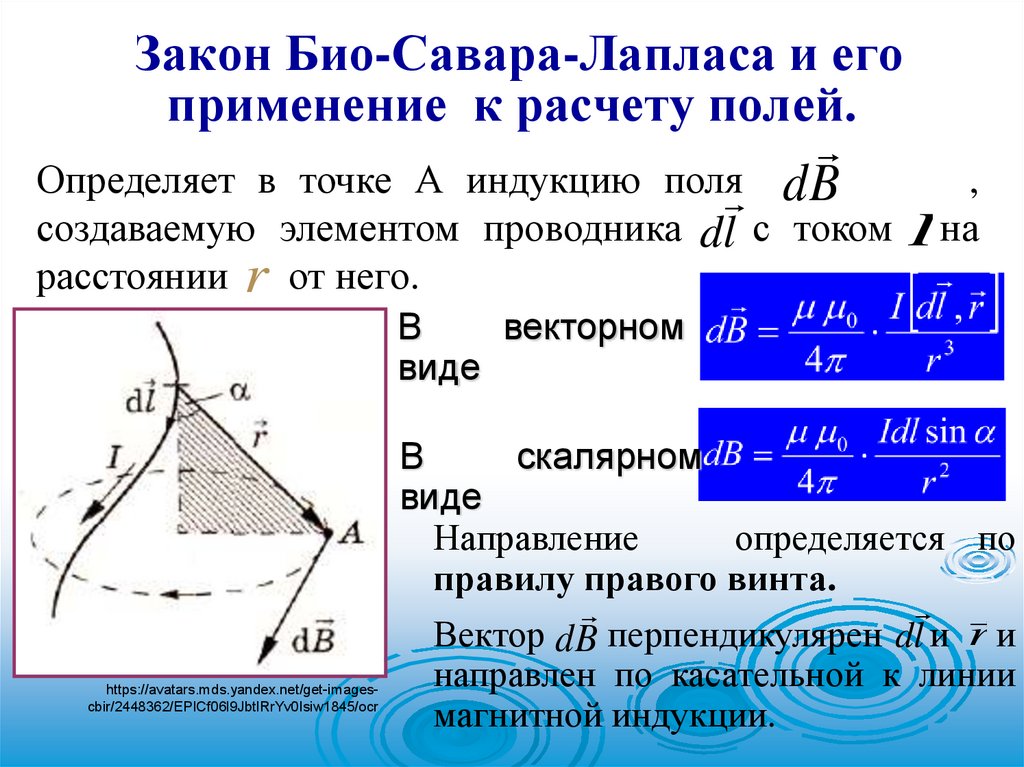
Закон Био-Савара-Лапласа и его
применение к расчету полей.
Определяет в точке А индукцию поля d B
,
создаваемую элементом проводника dl с током I на
расстоянии r от него.
В
векторном
виде
https://avatars.mds.yandex.net/get-imagescbir/2448362/EPICf06l9JbtlRrYv0Isiw1845/ocr
В
скалярном
виде
Направление
определяется по
правилу правого винта.
Вектор d B перпендикулярен dl и r и
направлен по касательной к линии
магнитной индукции.

13. Закон Био-Савара-Лапласа и его применение к расчету полей.

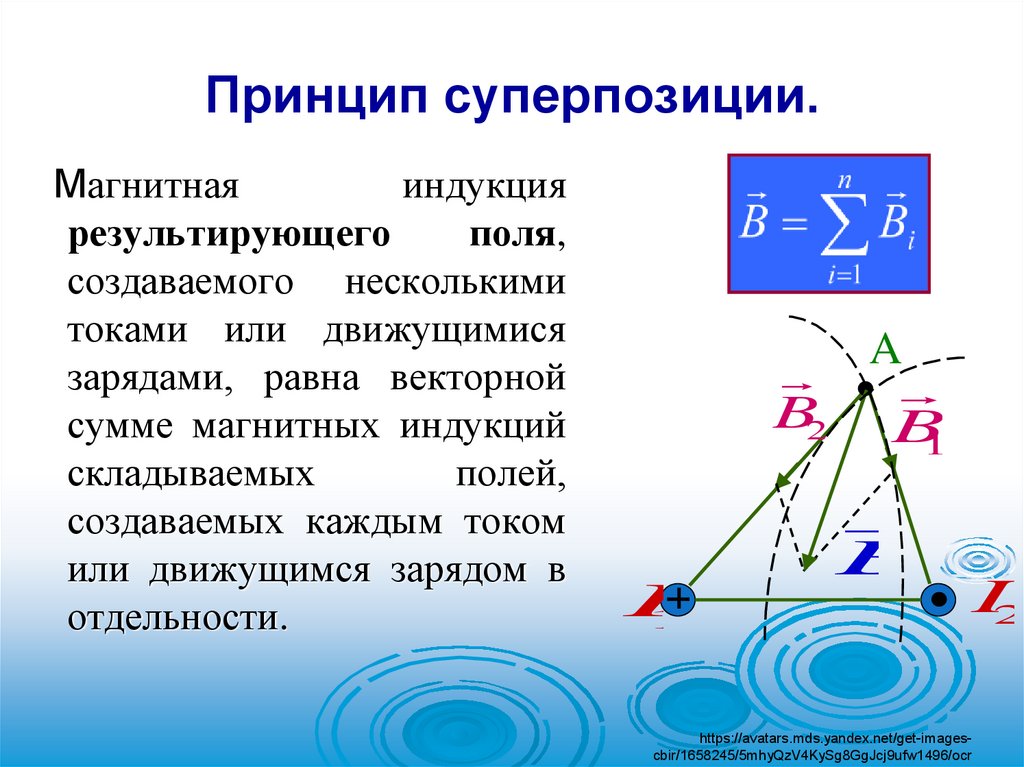
Принцип суперпозиции.
Магнитная
индукция
результирующего
поля,
создаваемого несколькими
токами или движущимися
зарядами, равна векторной
сумме магнитных индукций
складываемых
полей,
создаваемых каждым током
или движущимся зарядом в
отдельности.
B2
I
1
A
B1
B
I2
https://avatars.mds.yandex.net/get-imagescbir/1658245/5mhyQzV4KySg8GgJcj9ufw1496/ocr

14. Принцип суперпозиции.

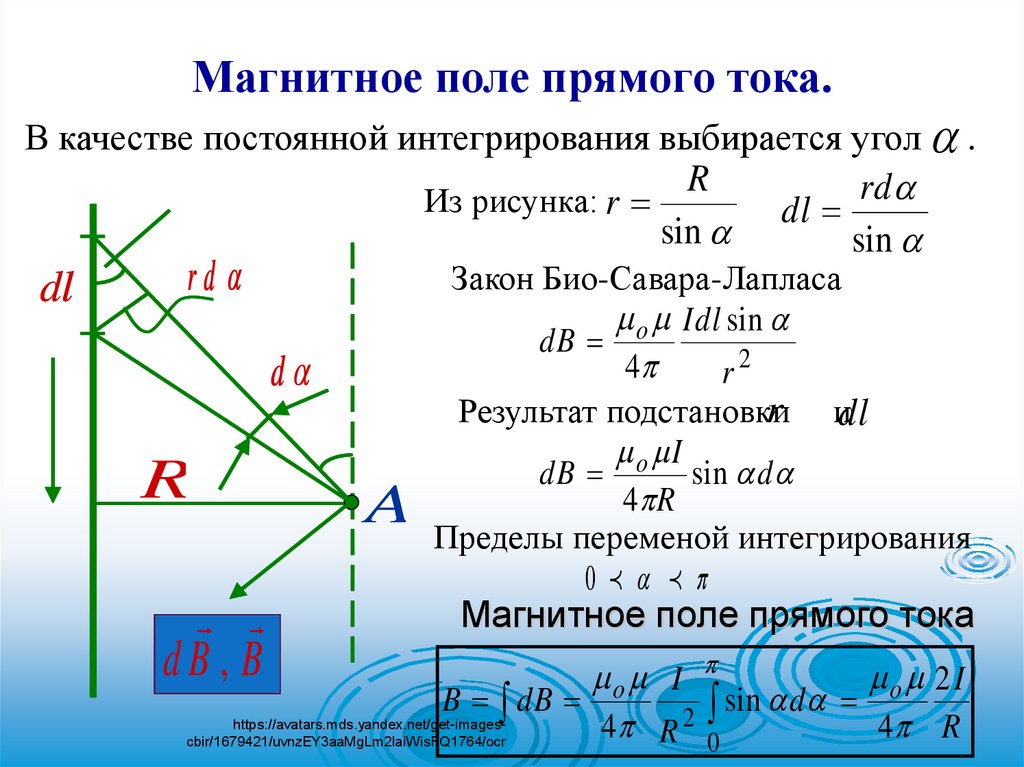
Магнитное поле прямого тока.
В качестве постоянной интегрирования выбирается угол .
R
rd
Из рисунка: r
dl
sin
sin
dl
rd
d
R
dB , B
A
Закон Био-Савара-Лапласа
Idl sin
dB o
4
r2
Результат подстановки
r иdl
o I
dB
sin d
4 R
Пределы переменой интегрирования
0
Магнитное поле прямого тока
o I
o 2I
B dB
sin d
2
4 R 0
4 R
https://avatars.mds.yandex.net/get-imagescbir/1679421/uvnzEY3aaMgLm2laiWisFQ1764/ocr

15. Магнитное поле прямого тока.

Магнитное поле в центре кругового
проводника с током.
Закон Био-Савара-Лапласа
dl
o Idl sin
dB
2
4
r
r с учётом
R sin 1
R
dB , B
o I
dB
dl
4 R 2
Магнитное поле в центре кругового проводника с
током
I
I
I
B dB
o
4 R
dl
2
o
4 R
2
R
o
2
2R

16. Магнитное поле в центре кругового проводника с током.

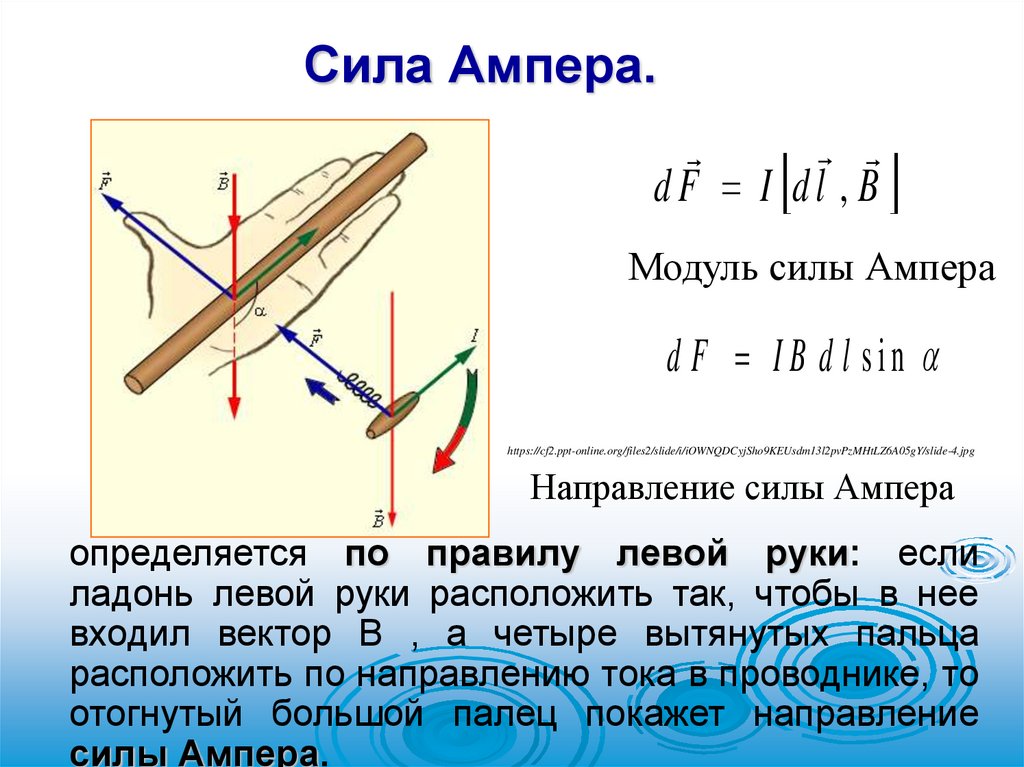
Сила Ампера.
d F I d l , B
Модуль силы Ампера
d F IB d l sin
https://cf2.ppt-online.org/files2/slide/i/iOWNQDCyjSho9KEUsdm13l2pvPzMHtLZ6A05gY/slide-4.jpg
Направление силы Ампера
определяется по правилу левой руки: если
ладонь левой руки расположить так, чтобы в нее
входил вектор В , а четыре вытянутых пальца
расположить по направлению тока в проводнике, то
отогнутый большой палец покажет направление
силы Ампера.

17.

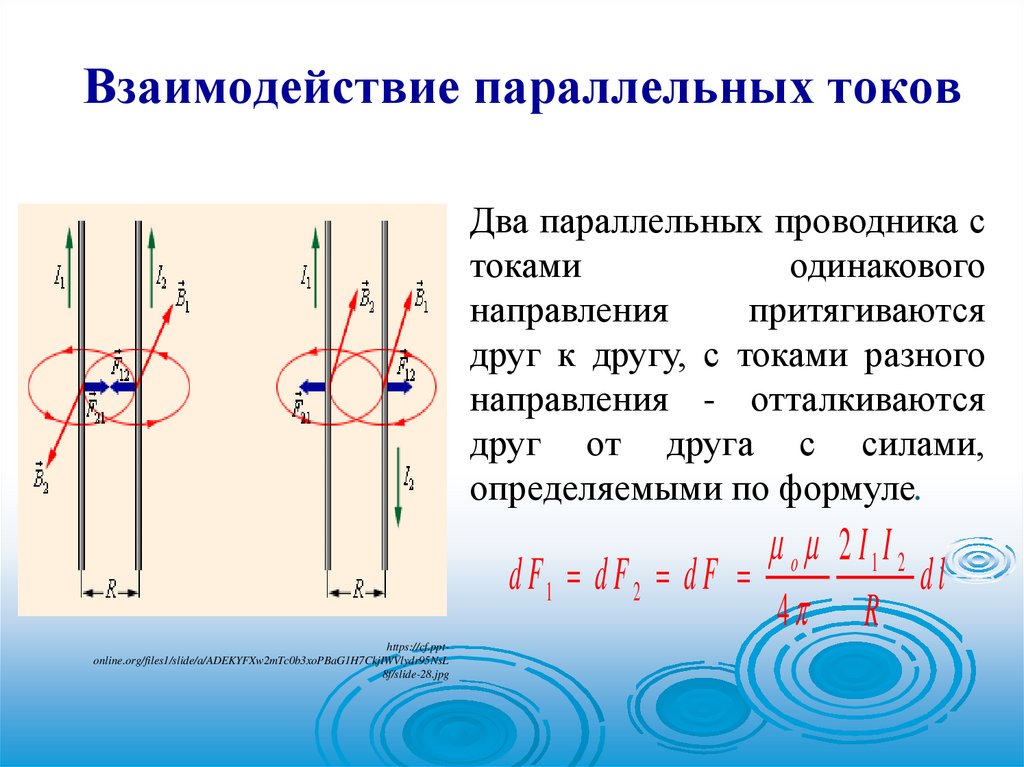
Взаимодействие параллельных токов
Два параллельных проводника с
токами
одинакового
направления
притягиваются
друг к другу, с токами разного
направления - отталкиваются
друг от друга с силами,
определяемыми по формуле.
o 2 I1I 2
d F1 d F 2 d F
dl
4 R
https://cf.pptonline.org/files1/slide/a/ADEKYFXw2mTc0b3xoPBaG1H7CkjIWVlydr95NsL
8f/slide-28.jpg

18. Взаимодействие параллельных токов

Магнитная постоянная
Если два параллельных проводника с
током находятся в вакууме ( =1), то
сила взаимодействия на единицу
длины проводника равна
Согласно определению Ампера при
значение
:
dF
o 2 I1I 2
dl
4 R
I1 I2 1 A
Rи 1 м
dF
2 1 0 7 Н / м
dl
Подставив это значение в формулу, получим
0 4 1 0 7 H / м 2 4 1 0 7 Г н / м

19. Магнитная постоянная

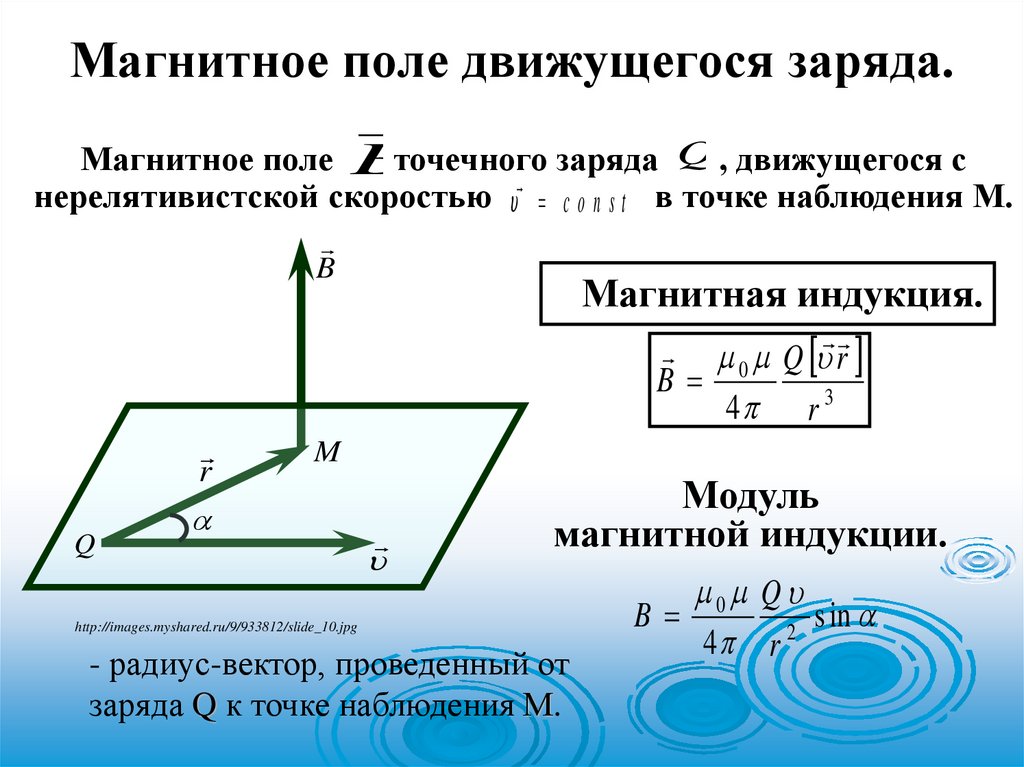
Магнитное поле движущегося заряда.
Магнитное поле B
точечного заряда Q , движущегося с
нерелятивистской скоростью c o n s t в точке наблюдения М.
B
Магнитная индукция.
0 Q r
B
4 r 3
r
Q
M
Модуль
магнитной индукции.
http://images.myshared.ru/9/933812/slide_10.jpg
- радиус-вектор, проведенный от
заряда Q к точке наблюдения М.
0 Q
B
s in
2
4 r

20. Магнитное поле движущегося заряда.

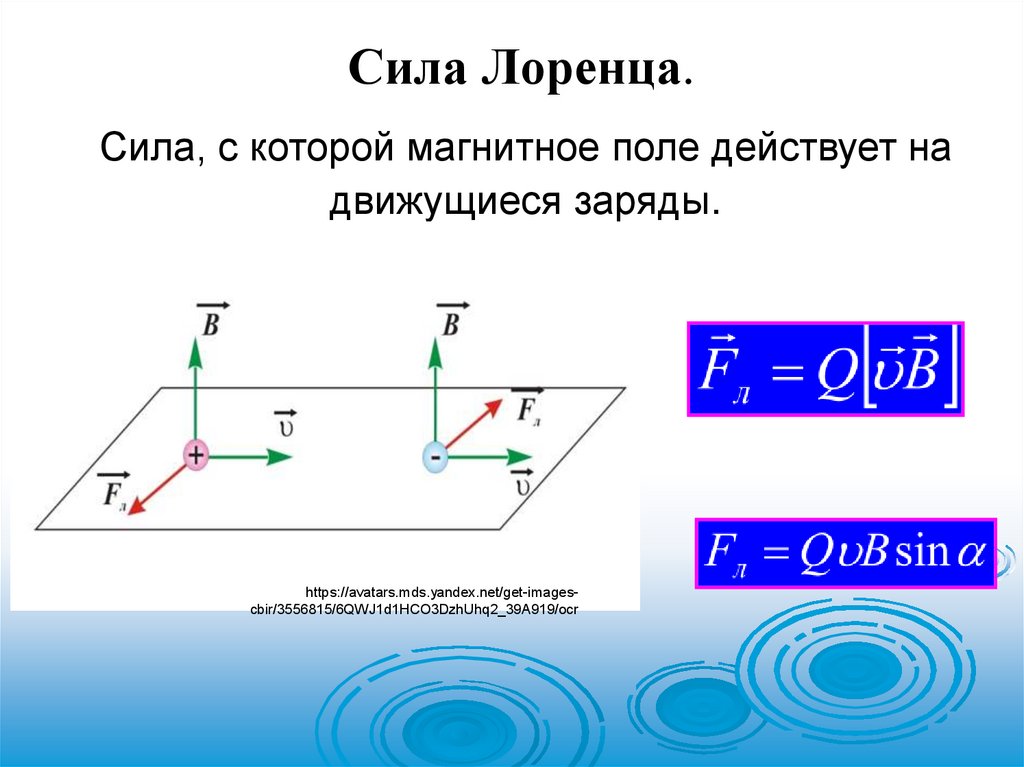
Сила Лоренца.
Сила, с которой магнитное поле действует на
движущиеся заряды.
https://fs.znanio.ru/methodology/images/2b/16/2b166762b33daf51b4
fbd28fc949056d14bc9509.jpg
https://avatars.mds.yandex.net/get-imagescbir/3556815/6QWJ1d1HCO3DzhUhq2_39A919/ocr

21. Сила Лоренца.

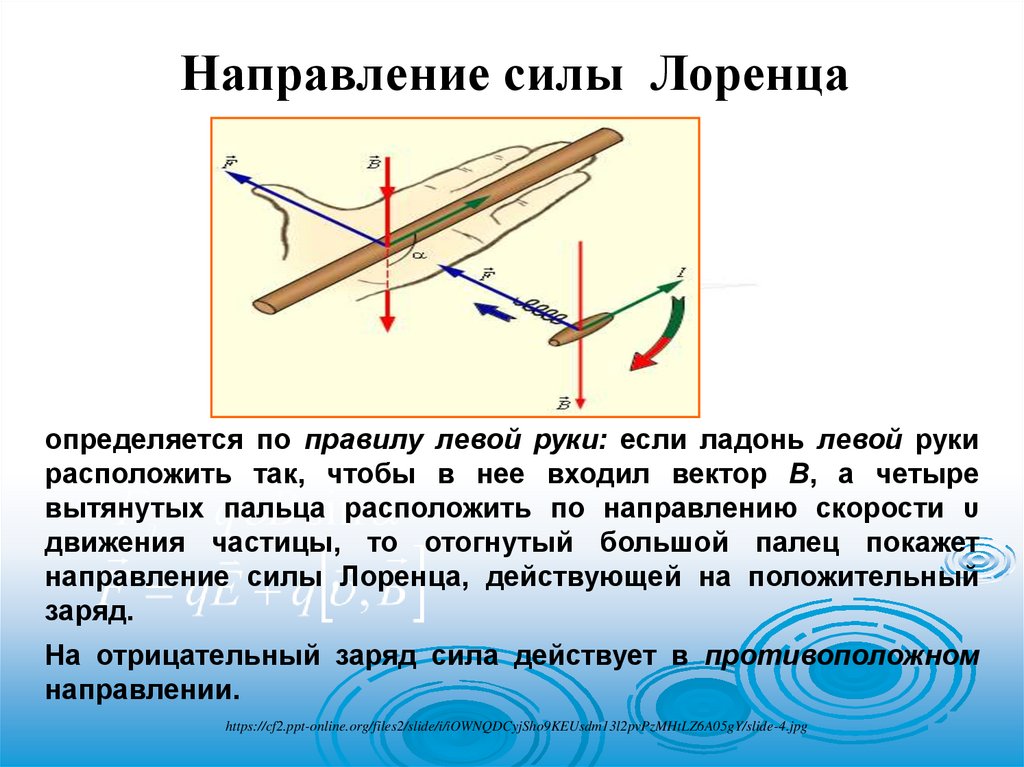
Направление силы Лоренца
определяется по правилу левой руки: если ладонь левой руки
расположить так, чтобы в нее входил вектор В, а четыре
вытянутых пальца расположить по направлению скорости υ
движения частицы, то отогнутый большой палец покажет
направление силы Лоренца, действующей на положительный
заряд.
На отрицательный заряд сила действует в противоположном
направлении.
https://cf2.ppt-online.org/files2/slide/i/iOWNQDCyjSho9KEUsdm13l2pvPzMHtLZ6A05gY/slide-4.jpg

22.

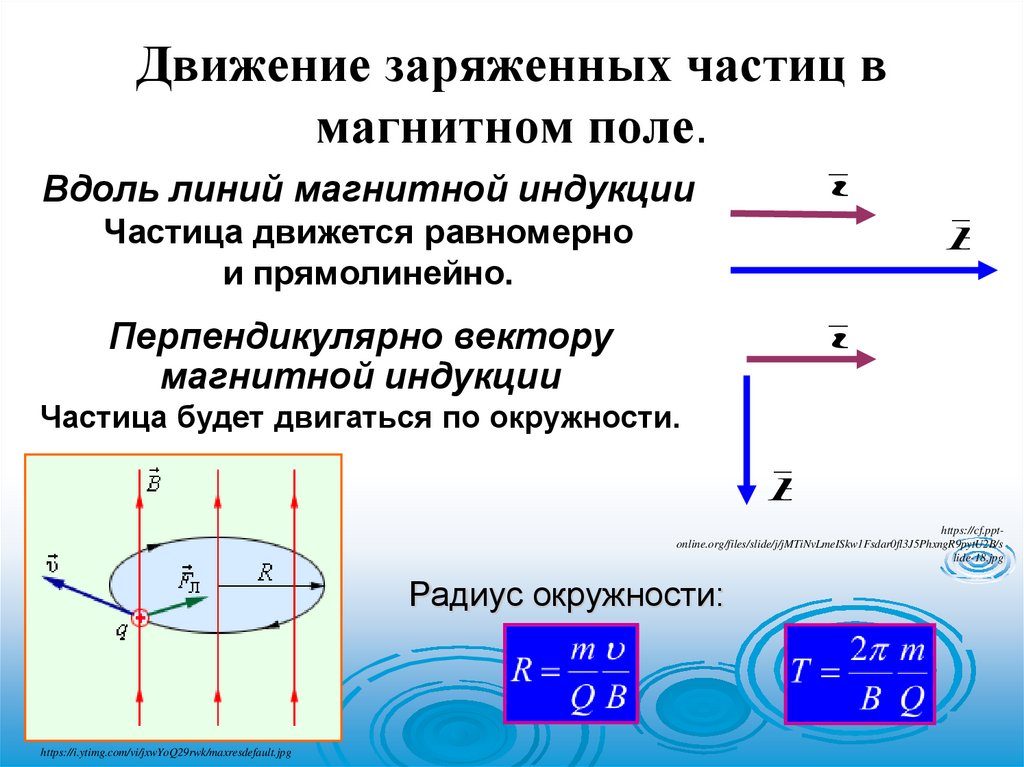
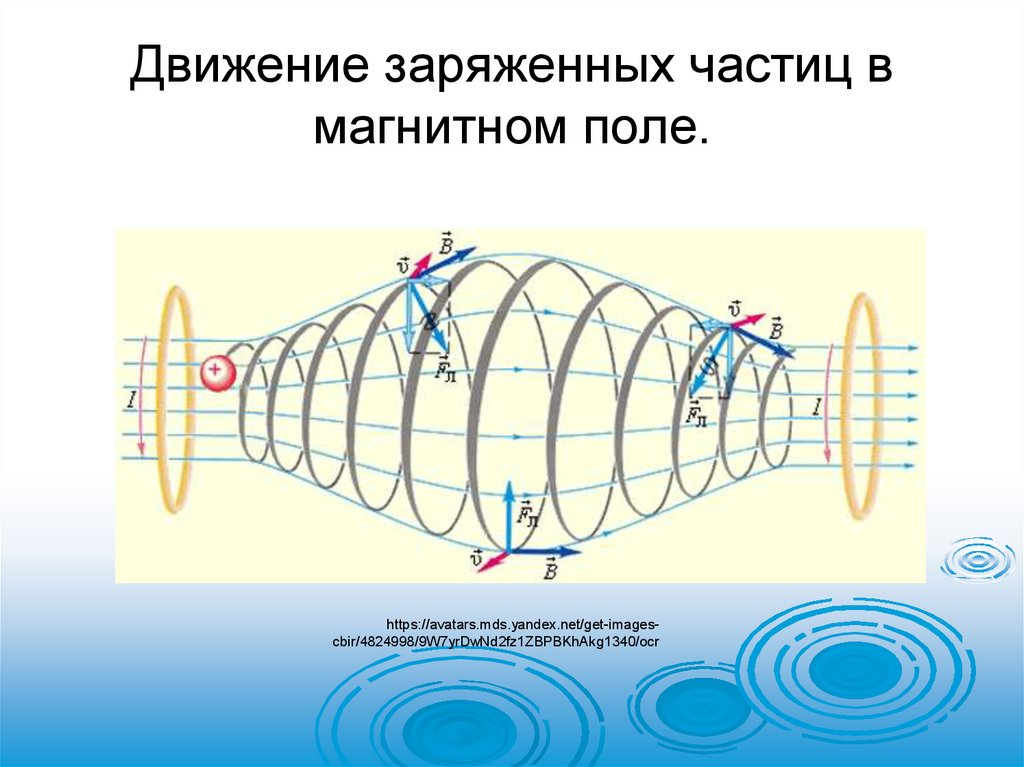
Движение заряженных частиц в
магнитном поле.
Вдоль линий магнитной индукции
Частица движется равномерно
и прямолинейно.
B
Перпендикулярно вектору
магнитной индукции
Частица будет двигаться по окружности.
B
https://cf.pptonline.org/files/slide/j/jMTiNvLmeISkw1Fsdar0fl3J5PhxngR9pytU2B/s
lide-18.jpg
Радиус окружности:
https://i.ytimg.com/vi/jxwYoQ29rwk/maxresdefault.jpg

23. Движение заряженных частиц в магнитном поле.

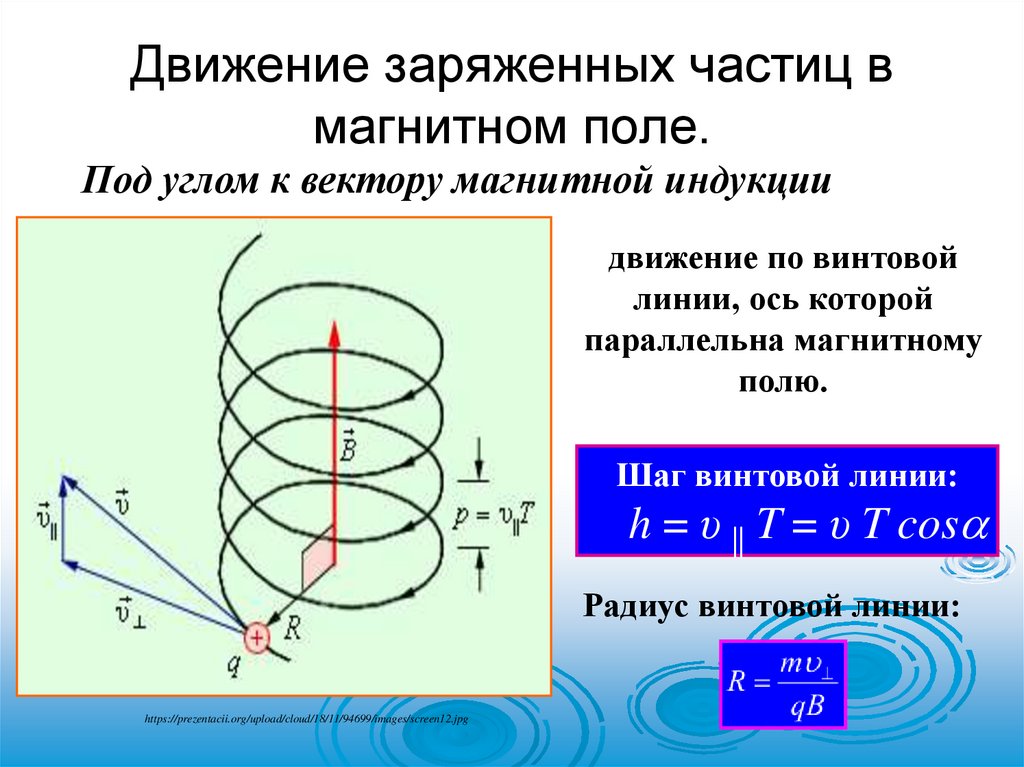
Под углом к вектору магнитной индукции
движение по винтовой
линии, ось которой
параллельна магнитному
полю.
Шаг винтовой линии:
h = υ || T = υ T cos
Радиус винтовой линии:
https://prezentacii.org/upload/cloud/18/11/94699/images/screen12.jpg

24. Движение заряженных частиц в магнитном поле.

https://avatars.mds.yandex.net/get-imagescbir/4824998/9W7yrDwNd2fz1ZBPBKhAkg1340/ocr

25. Движение заряженных частиц в магнитном поле.

Закон полного тока.
(теорема о циркуляции вектора магнитной индукции
В
)
Циркуляцией вектора В по заданному
Bdl B dl
замкнутому контуру называется интеграл:
L
L
l
Bl=Bcos
—
составляющая
вектора
В
в
направлении
касательной к контуру, — угол
между векторами В и dl.
https://avatars.mds.yandex.net/get-images-cbir/2187997/BWD-shEgQ1m_Quq3QNkqA1207/ocr
Циркуляция вектора В по произвольному замкнутому
контуру равна произведению магнитной постоянной на
алгебраическую сумму токов, охватываемых этим
контуром.

26.

Теорема о циркуляции вектора В
(закон полного тока) в вакууме
Из курса электростатики известно, что
циркуляция вектора электростатического
поля всегда равна нулю, то есть такое
поле является потенциальным.
Циркуляция вектора магнитного поля
не равна нулю. Такое поле называется
вихревым или соленоидальным.

27. Теорема о циркуляции вектора В (закон полного тока) в вакууме

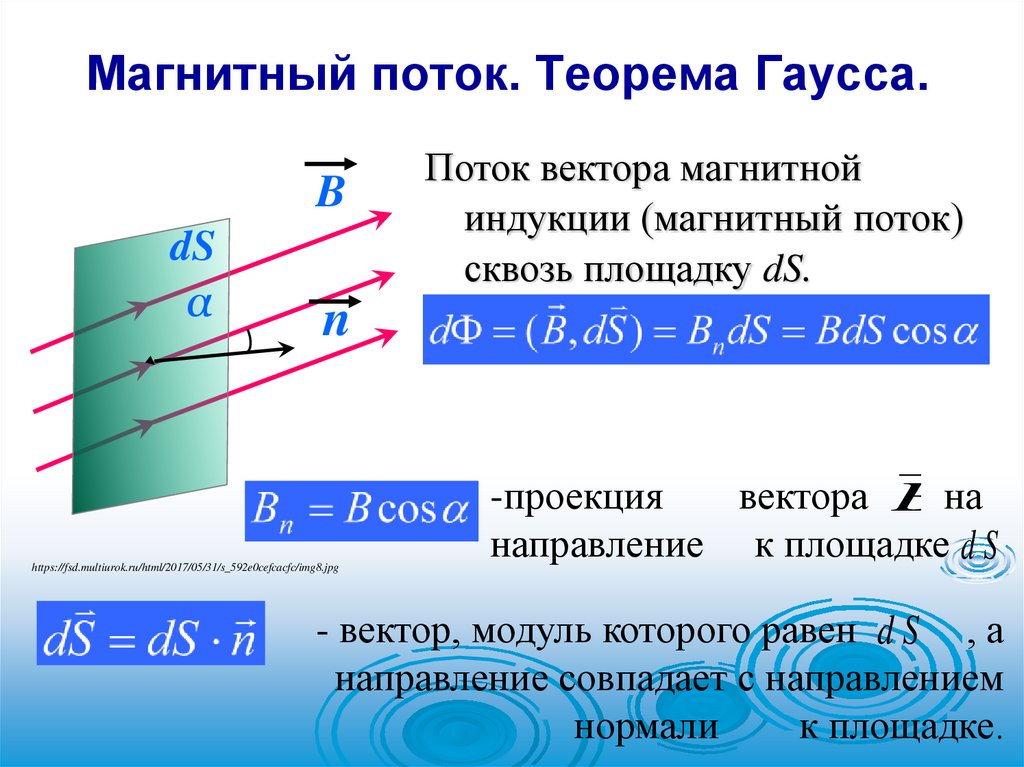
Магнитный поток. Теорема Гаусса.
B
dS
α
Поток вектора магнитной
индукции (магнитный поток)
сквозь площадку dS.
n
https://fsd.multiurok.ru/html/2017/05/31/s_592e0cefcacfc/img8.jpg
-проекция
вектора Bна
направление к площадке d S
- вектор, модуль которого равен d S , а
направление совпадает с направлением
нормали
к площадке.

28. Магнитный поток. Теорема Гаусса.

Теорема Гаусса для поля B .
Магнитный поток сквозь произвольную поверхность S
:
B BdS Bn dS
S
S
(Интеграл берётся по произвольной поверхности S )
B Вб Тл м
2
1 Вб — магнитный поток, проходящий сквозь плоскую
поверхность площадью 1 м2, расположенную
перпендикулярно однородному магнитному полю,
индукция которого равна 1 Тл (1 Вб=1 Тл м2).

29.

Теорема Гаусса для магнитного поля
в вакууме
Поток вектора магнитной
индукции сквозь произвольную
замкнутую поверхность равен
нулю:
ФB BdS 0
S
https://avatars.mds.yandex.net/get-imagescbir/1979567/WefsG6acHAiNRHJgqZgiRw1124/ocr
Эта
теорема
отражает
факт
отсутствия магнитных зарядов,
вследствие чего линии магнитной
индукции не имеют ни начала, ни
конца и являются замкнутыми.

30. Теорема Гаусса для магнитного поля в вакууме

Работа по перемещению проводника с
током в магнитном поле
Работа магнитного поля, в отличие
от работы электростатического
поля, зависит от пути перехода
проводника из начального в
конечное положение.
Работа
по
перемещению
проводника с током в магнитном
поле равна произведению силы
https://avatars.mds.yandex.net/get-imagescbir/2971222/hMUkWygmLFGaWObh_ILQyA1026/ocr тока
на
магнитный
поток,
пересеченный
движущимся
проводником

31.

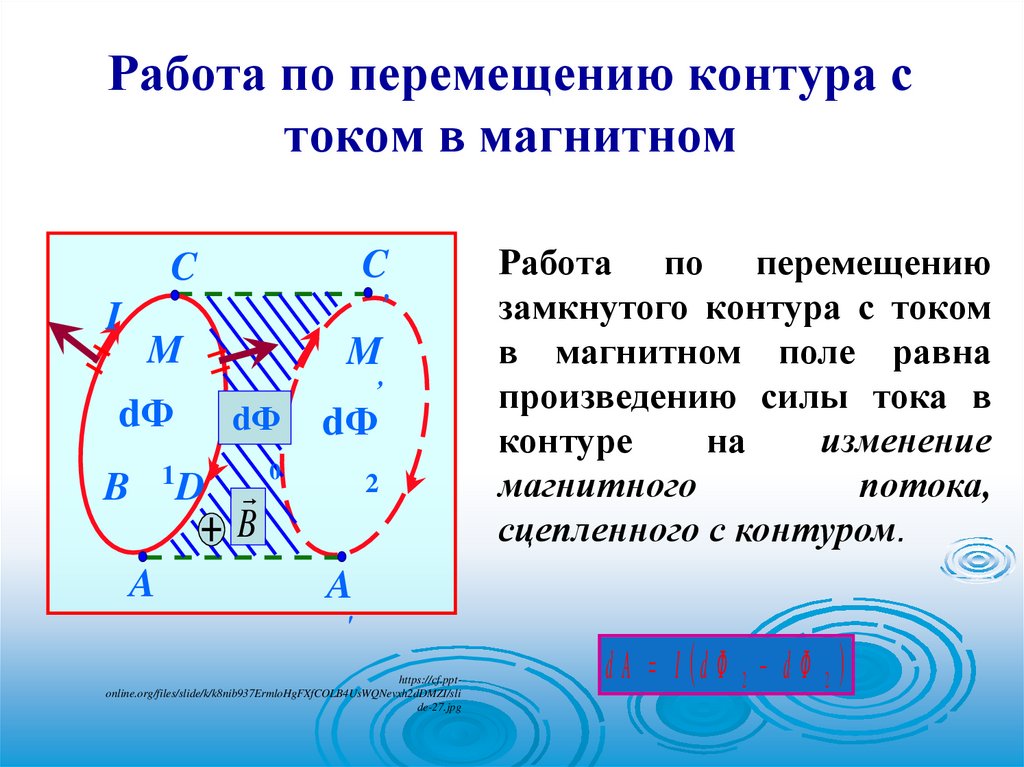
Работа по перемещению контура с
током в магнитном
C
C
’
I
M
dФ
B
A
1
M
’
dФ
dФ
0
2
D
B
Работа по перемещению
замкнутого контура с током
в магнитном поле равна
произведению силы тока в
контуре
на
изменение
магнитного
потока,
сцепленного с контуром.
A
'
https://cf.pptonline.org/files/slide/k/k8nib937ErmloHgFXfCOLB4UsWQNevxh2dDMZI/sli
de-27.jpg
d A I d Ф 2 d Ф 2

32. Работа по перемещению контура с током в магнитном

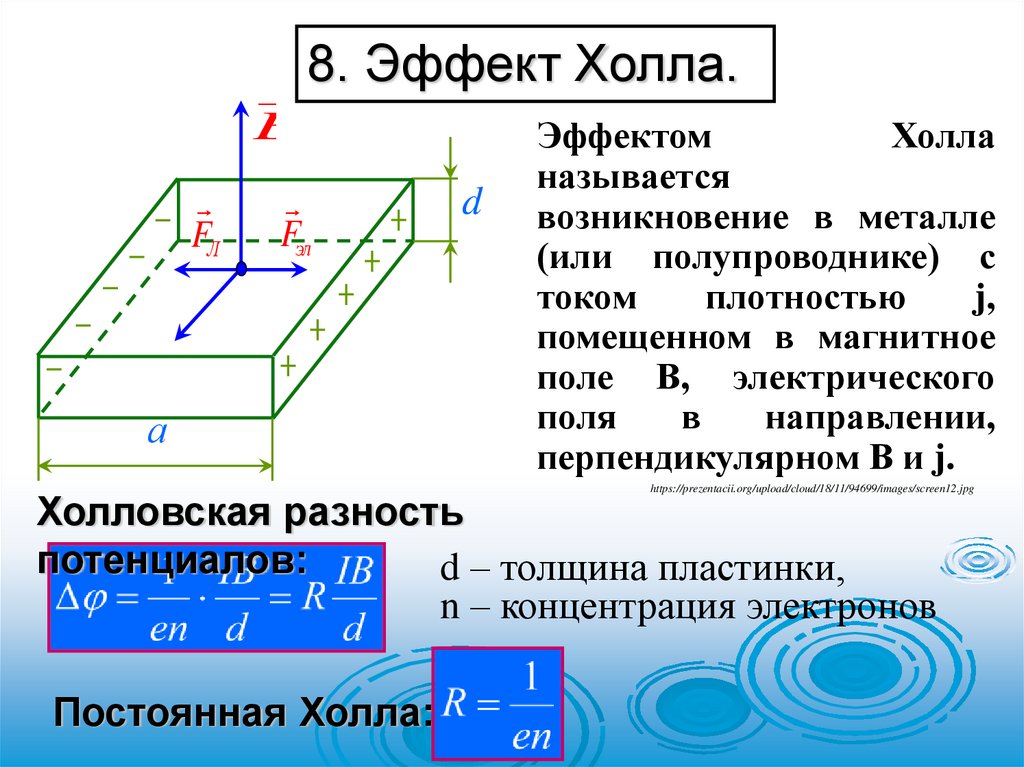
8.
Эффект
Холла.
B
FЛ
Fэл
а
d
Эффектом
Холла
называется
возникновение в металле
(или полупроводнике) с
током
плотностью
j,
помещенном в магнитное
поле В, электрического
поля
в
направлении,
перпендикулярном В и j.
https://prezentacii.org/upload/cloud/18/11/94699/images/screen12.jpg
Холловская разность
потенциалов:
d – толщина пластинки,
n – концентрация электронов
Постоянная Холла:

33.

Карагандинский технический университе им. А.Сагинова
Кафедра физики
ЭЛЕКТРОМАГНИТНАЯ
ИНДУКЦИЯ
Для всех специальностей.
Автор: к.х.н., старший преподаватель кафедры физики
Кусенова А.С.

34. Кафедра физики

План лекции
Явление электромагнитной индукции.
Опыты Фарадея
Закон Фарадея. Правила Ленца.
Вращение рамки в магнитном поле.
Индуктивность контура.
Самоиндукция. Индуктивность
соленоида.
Токи при размыкании и замыкании.
Взаимная индукция. Трансформаторы.
Энергия магнитного поля. Объемная плотность энергии
магнитного поля.
►https://youtu.be/Ff1B27GKusA

35.

Явление электромагнитной
индукции. Опыты Фарадея
В 1831 году английский физик Майкл Фарадей
открыл явление электромагнитной индукции.
Явление электромагнитной индукции –
возникновение электрического тока в
замкнутом
проводящем контуре при
изменении потока магнитной индукции,.

36.

ОПЫТЫ ФАРАДЕЯ
https://cf.ppt-online.org/files1/slide/l/LbQ3VDO4NponTSC7AIe9tzkm05UFrJHw1sKGd8PWvf/slide4.jpg
https://shareslide.ru/img/thumbs/cbeecb71d228a0b028be9c8e76613341800x.jpg
https://shareslide.ru/img/thumbs/cbeecb71d228a0b028be9c8e76613341-800x.jp

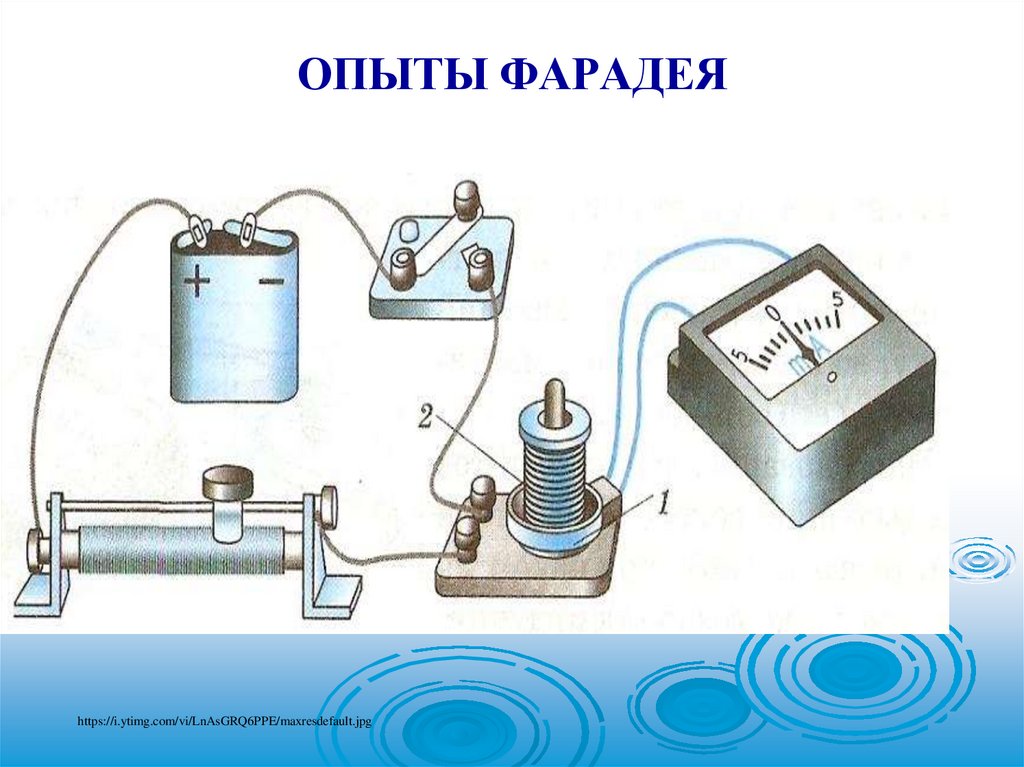
37. ОПЫТЫ ФАРАДЕЯ

https://i.ytimg.com/vi/LnAsGRQ6PPE/maxresdefault.jpg

38. ОПЫТЫ ФАРАДЕЯ

Индукционный ток возникает
всегда,
когда
происходит
изменение
сцепленного
с
контуром потока магнитной
индукции
Сила индукционного тока совершенно не зависит от способа
изменения потока магнитной
индукции, а определяется лишь
скоростью его изменения
https://i.ytimg.com/vi/LnAsGRQ6PPE/maxresdefault.jpg

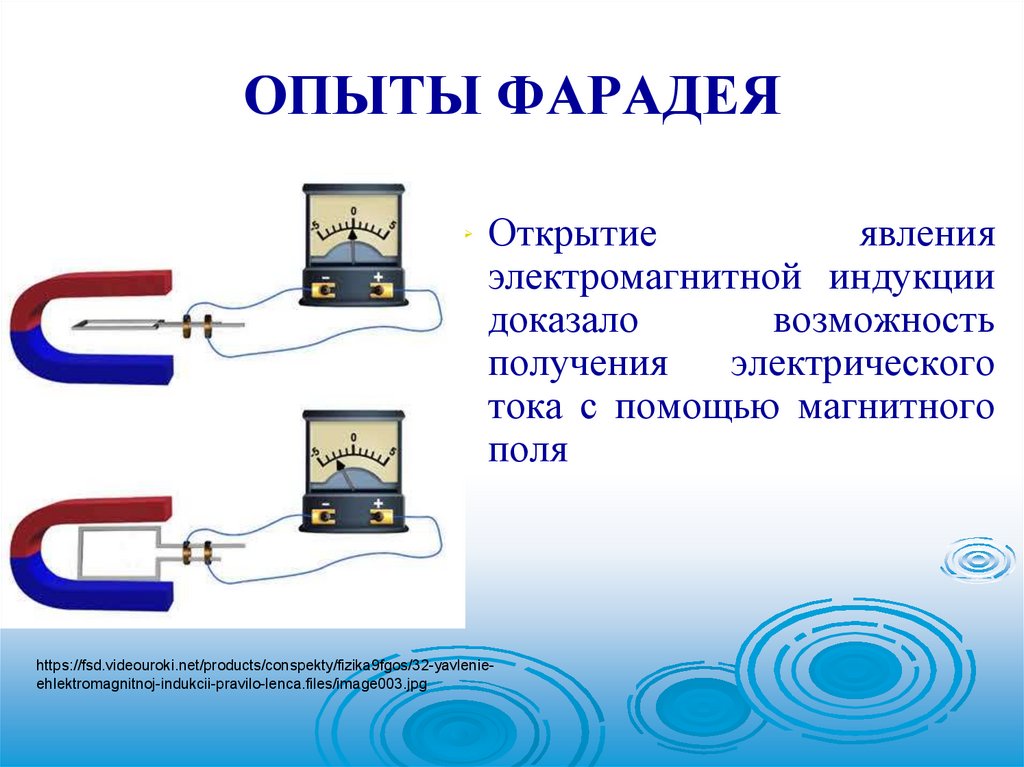
39. ОПЫТЫ ФАРАДЕЯ

Открытие
явления
электромагнитной индукции
доказало
возможность
получения
электрического
тока с помощью магнитного
поля
https://fsd.videouroki.net/products/conspekty/fizika9fgos/32-yavlenieehlektromagnitnoj-indukcii-pravilo-lenca.files/image003.jpg

40. ОПЫТЫ ФАРАДЕЯ

Закон Фарадея
Всякий раз, когда происходит изменение сцепленного с
контуром потока магнитной индукции, в контуре возникает
индукционный ток; возникновение индукционного тока
указывает на наличие в цепи электродвижущей силы,
называемой электродвижущей силой электромагнитной
индукции.
ЭДС электромагнитной индукции в контуре численно
равна и противоположна по знаку скорости изменения
магнитного потока сквозь поверхность, ограниченную
этим контуром.
d i
d i
0 0
0
0
i
i
dt
dt
N i
d i
i N
dt

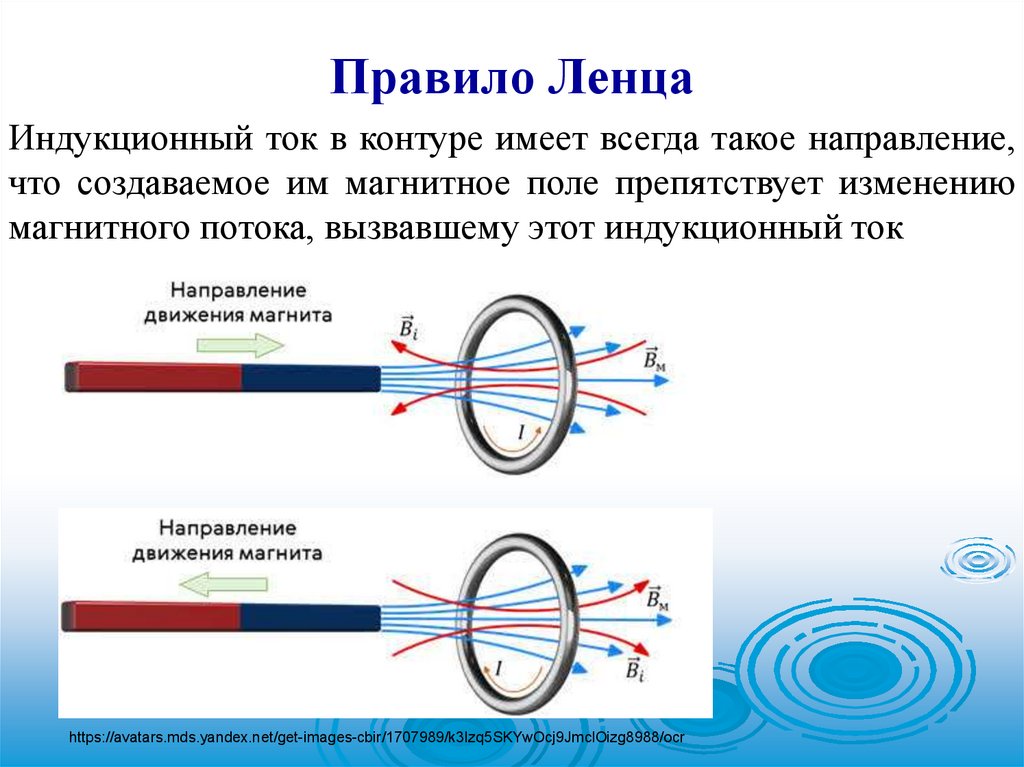
41. Закон Фарадея

Правило Ленца
Индукционный ток в контуре имеет всегда такое направление,
что создаваемое им магнитное поле препятствует изменению
магнитного потока, вызвавшему этот индукционный ток
https://avatars.mds.yandex.net/get-images-cbir/1707989/k3Izq5SKYwOcj9JmclOizg8988/ocr

42.

Вращение рамки в магнитном поле.
https://obrazovaka.ru/wp-content/images/predmet/fizika-147765-vraschenieramki-v-magnitnom-pole.jpg
Если
в однородном магнитном поле равномерно
вращается рамка, то в ней возникает переменная э.д.с.,
изменяющаяся по гармоническому закону. Если по
рамке, помещенной в магнитное поле, пропускать
электрический ток, то на нее будет действовать
вращающий момент и рамка начнет вращаться. На
этом принципе основана работа электродвигателей.

43. Вращение рамки в магнитном поле.

Э.д.с. индукции на концах движущегося
в магнитном поле проводника
i B
https://i.ytimg.com/vi/LnAsGRQ6PPE/maxresdefault.jpg

44.

ИНДУКТИВТНОСТЬ КОНТУРА
Сцепленный с контуром магнитный
пропорционален току в контуре:
поток
Ф = LI
Коэффициент пропорциональности L называется
индуктивностью контура Единица индуктивности
в СИ генри (Гн):
1 Гн = 1 Вб/1 А. .
ИНДУКТИВТНОСТЬ СОЛЕНОИДА
Полный
магнитный
поток
сквозь
(потокосцепление) равен:
соленоид

45. ИНДУКТИВТНОСТЬ КОНТУРА

САМОИНДУКЦИЯ
Явление возникновение э.д.с. индукции в
проводящем контуре при изменении в нем силы
тока называется самоиндукцией.
ЭДС самоиндукции пропорциональна скорости
изменения силы тока в контуре, знак минус,
обусловленный правилом Ленца, показывает, что
наличие индуктивности в контуре приводит к
замедлению изменения тока в нем.

46. САМОИНДУКЦИЯ

ТОКИ ПРИ РАЗМЫКАНИИ И
ЗАМЫКАНИИ
При
всяком изменении силы тока в
проводящем контуре возникает э.д.с.
самоиндукции, в результате чего в
контуре появляются дополнительные
токи,
называемые
экстратоками
самоиндукции

47. ТОКИ ПРИ РАЗМЫКАНИИ И ЗАМЫКАНИИ

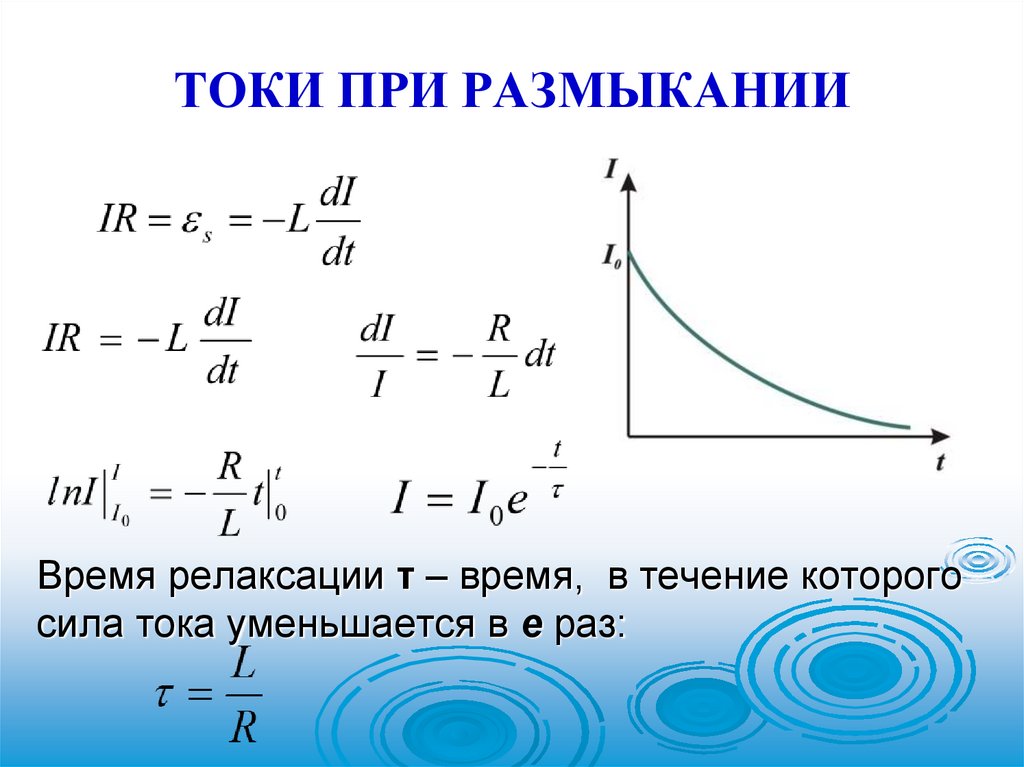
ТОКИ ПРИ РАЗМЫКАНИИ
Время релаксации τ – время, в течение которого
сила тока уменьшается в е раз:

48. ТОКИ ПРИ РАЗМЫКАНИИ

При
значительном
увеличении
сопротивления
цепи (R >> R0),
обладающей большой индуктивностью, э.д.с.
самоиндукции может во много раз
превышать
э.д.с.
источника
тока,
включенного в цепь. Поэтому контур,
содержащий индуктивность, нельзя резко
размыкать, т.к. это может привести к пробою
изоляции и выводу из строя измерительных
приборов

49.

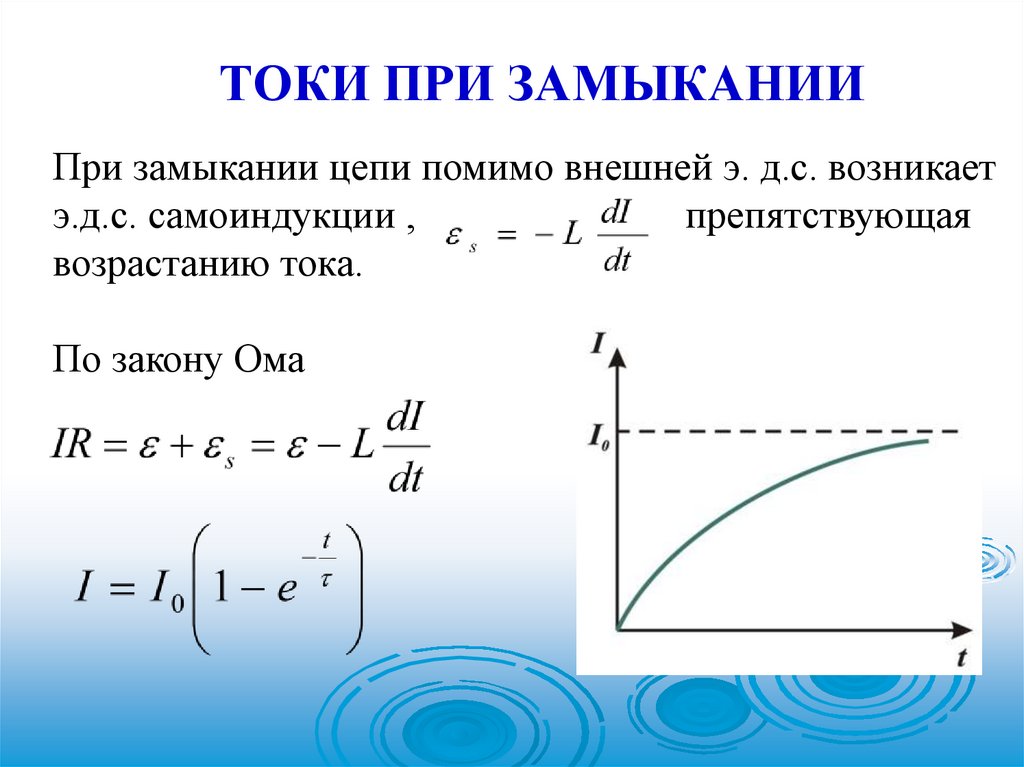
ТОКИ ПРИ ЗАМЫКАНИИ
При замыкании цепи помимо внешней э. д.с. возникает
э.д.с. самоиндукции ,
препятствующая
возрастанию тока.
По закону Ома

50. ТОКИ ПРИ ЗАМЫКАНИИ

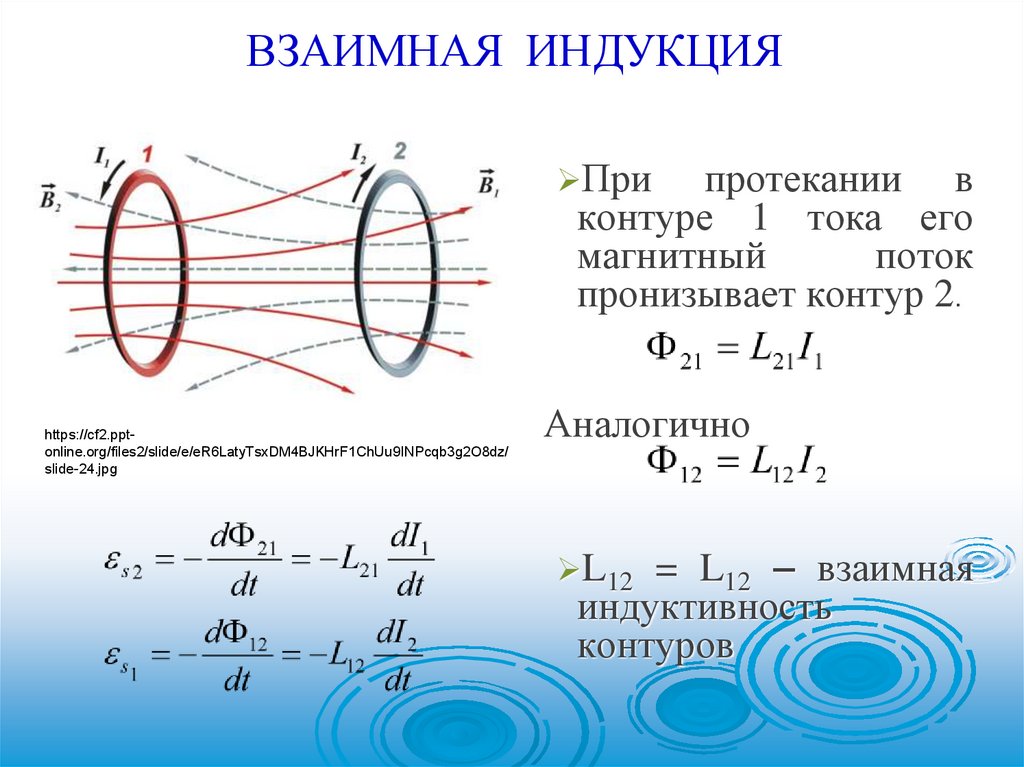
ВЗАИМНАЯ ИНДУКЦИЯ
При
протекании в
контуре 1 тока его
магнитный
поток
пронизывает контур 2.
https://cf2.pptonline.org/files2/slide/e/eR6LatyTsxDM4BJKHrF1ChUu9INPcqb3g2O8dz/
slide-24.jpg
Аналогично
L12 = L12 – взаимная
индуктивность
контуров

51. ВЗАИМНАЯ ИНДУКЦИЯ

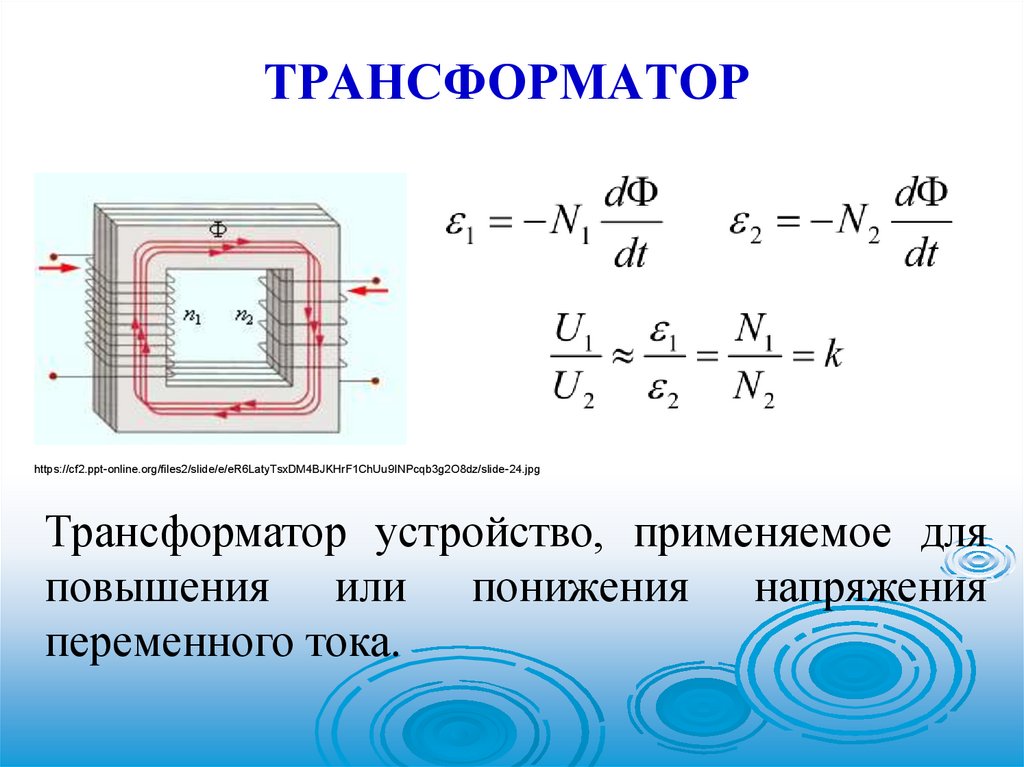
ТРАНСФОРМАТОР
https://cf2.ppt-online.org/files2/slide/e/eR6LatyTsxDM4BJKHrF1ChUu9INPcqb3g2O8dz/slide-24.jpg
Трансформатор устройство, применяемое для
повышения или понижения напряжения
переменного тока.

52. ТРАНСФОРМАТОР

Энергия магнитного поля
Магнитное поле является носителем энергии.
Энергия магнитного поля равна работе, которая
затрачивается током на создание этого поля:
2 2
1
N I
W 0
S
2

53. Энергия магнитного поля

Объемная плотность энергии
магнитного поля
Данная
формула
справедлива
как
для
однородного, так и для неоднородного полей, но
только для сред, для которых зависимость В и Н
линейная, т.е. она относится только к пара- и
диамагнетикам.

54. Объемная плотность энергии магнитного поля

Карагандинский государственный
технический университет
Физика
ФИЗИКА 1
кафедрасы
МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

55.

План лекции
Виды магнетиков
Гипотеза Ампера
Намагниченность
Природа диа- и парамагнетизма
Ферромагнетики
Магнитный гистерезис

56.

Магнитные свойства вещества
Всякое вещество является магнетиком,
то есть способно под действием
магнитного поля намагничиваться –
приобретать магнитный момент.
Магнетики – тела, обладающие
магнитными свойствами.
Магнитными свойствами обладают
не только макроскопические тела, но
и отдельные молекулы, атомы,
атомные ядра
https://avatars.mds.yandex.net/get-imagescbir/1620113/UOTlXR9IkpGyDTilcd8pag4419/ocr
Магнитные свойства вещества зависят от структуры их
атомов и атомных ядер, а также характера
взаимодействия между ними

57.

АНАЛОГИЯ МЕЖДУ
ДИЭЛЕКТРИКАМИ И МАГНЕТИКАМИ
диэлектрики
магнетики
электрическое
поле
магнитное
поле
Измене
ние
поля
Изменени
Измене Измене
е свойств
ние
ние
диэлектр
поля
свойств
Для качественного
ика объяснения магнитных явлений
магнети
воспользуемся гипотезой Ампера.
ка

58.

https://avatars.mds.yandex.net/get-imagescbir/2493011/6l12HESnz8pVes-3f3aX1w8336/ocr
ГИПОТЕЗА АМПЕРА
В любом теле существуют микроскопические токи,
обусловленные движением электронов в атомах и молекулах.
Движение
электрона
по
орбите
эквивалентно круговому току, поэтому
он обладает орбитальным магнитным
моментом
q e
Ie
t T
pm
Ie
+
Le
e 2
2
pm I e S R e R
T
2 R
T
e R 2
eR
pm
2 R
2
орбитальный магнитный
момент электрона

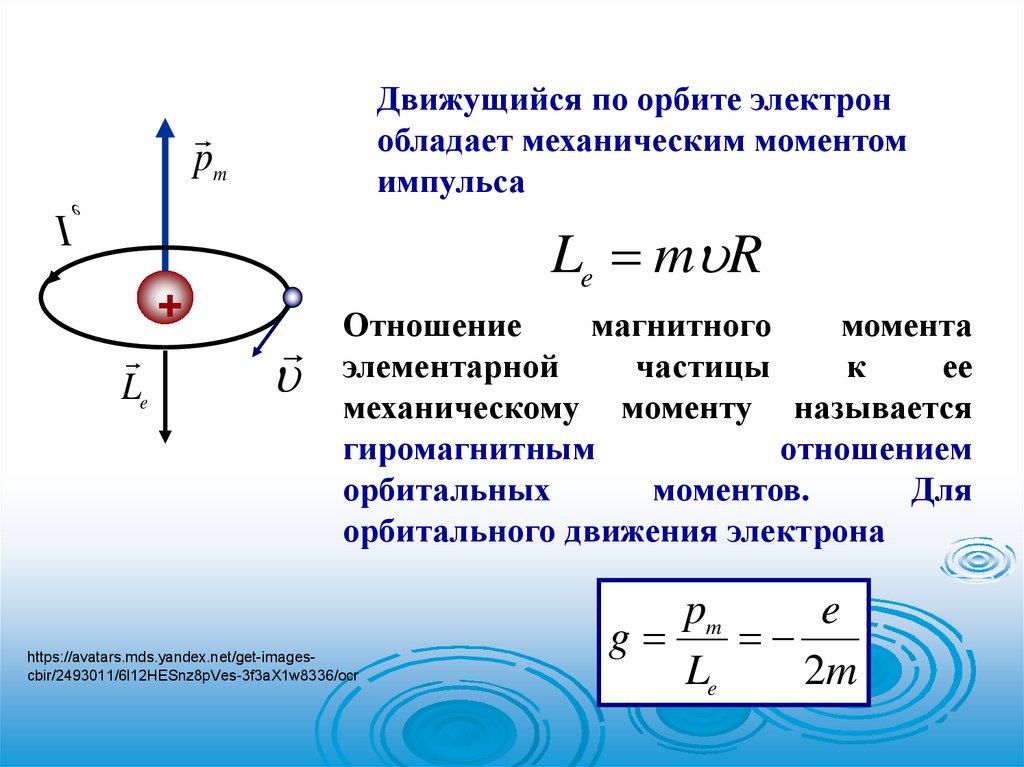
59.

Движущийся по орбите электрон
обладает механическим моментом
импульса
pm
Ie
+
Le
Le m R
Отношение
магнитного
момента
элементарной
частицы
к
ее
механическому моменту называется
гиромагнитным
отношением
орбитальных
моментов.
Для
орбитального движения электрона
https://avatars.mds.yandex.net/get-imagescbir/2493011/6l12HESnz8pVes-3f3aX1w8336/ocr
pm
e
g
Le
2m

60.

Магнитные моменты атомов
Кроме орбитальных моментов электрон обладает собственным
механическим моментом импульса Les, называемым спином,
который является неотъемлемым свойством электрона, подобно
его заряду и массе. Спину электрона Les, соответствует
собственный (спиновый) магнитный момент рms, пропорциональный Les и направленный в противоположную сторону
Общий магнитный момент атома
(молекулы) pa равен векторной сумме
магнитных моментов (орбитальных и
спиновых) входящих в атом (молекулу)
электронов
pa pm pms
https://avatars.mds.yandex.net/get-imagescbir/2950611/lyTU8U_0SAooDYKNfTNvOw9487/ocr

61.

ВИДЫ МАГНЕТИКОВ
Диамагнетики
Парамагнетики
Ферромагнетики

62.

Намагниченность
Для количественного описания намагничения магнетиков вводят
векторную величину — намагниченность, определяемую
магнитным моментом единицы объема магнетика:
Pm
pa
J
V
V
Магнитное поле в веществе складывается из двух полей:
внешнего поля В0 (поля, создаваемого намагничивающим током
в вакууме), и поля, создаваемого намагниченным веществом В'
(поля, создаваемого молекулярными микротоками).
B B0 B'
B0 = 0 H
B
B0
Магнитная проницаемость показывает, во сколько раз индукция
магнитного поля в веществе больше, чем в вакууме.

63.

Намагниченность
Кроме магнитной проницаемости магнитные
характеризует магнитная восприимчивость:
B' m B0
свойства
B 1 m B0
B
H = J
0
В несильных полях намагниченность прямо пропорциональна
напряженности поля, вызывающего намагничение
J m H
1 m

64.

B' B0 диамагнетик
m 0
μ > 1 B' B0 парамагнетик
m 0
μ< 1
1 B' B0 ферромагнетик m 0

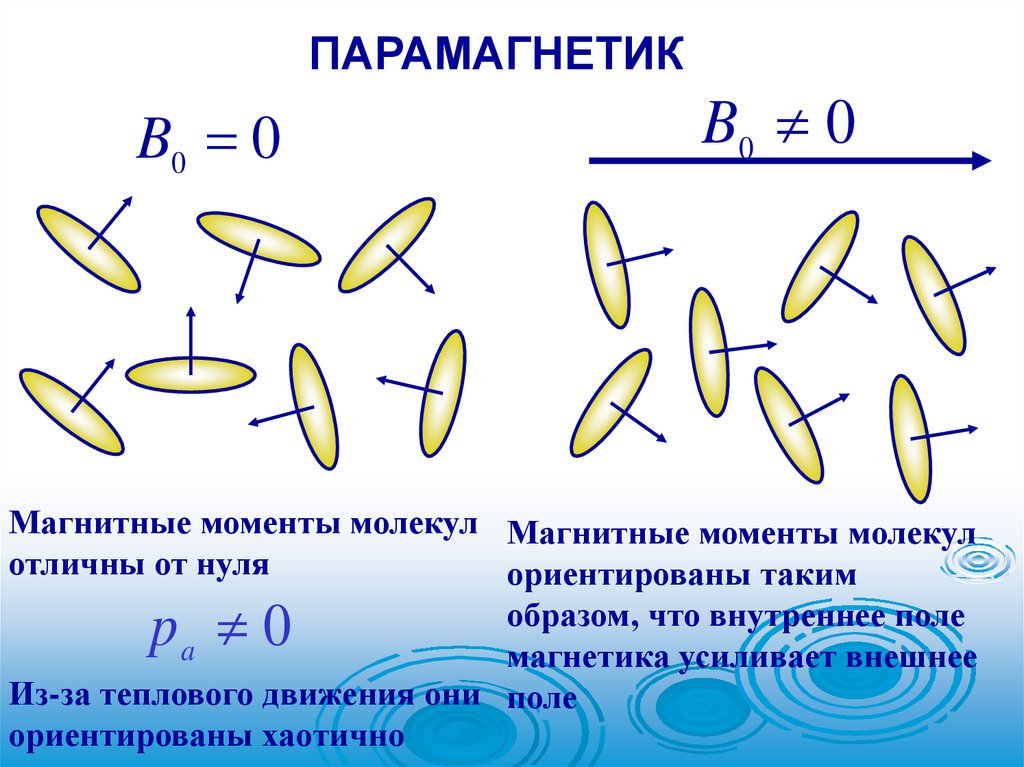
65.

ПАРАМАГНЕТИК
B0 0
B0 0
Магнитные моменты молекул Магнитные моменты молекул
отличны от нуля
ориентированы таким
образом, что внутреннее поле
a
магнетика усиливает внешнее
Из-за теплового движения они поле
ориентированы хаотично
p 0

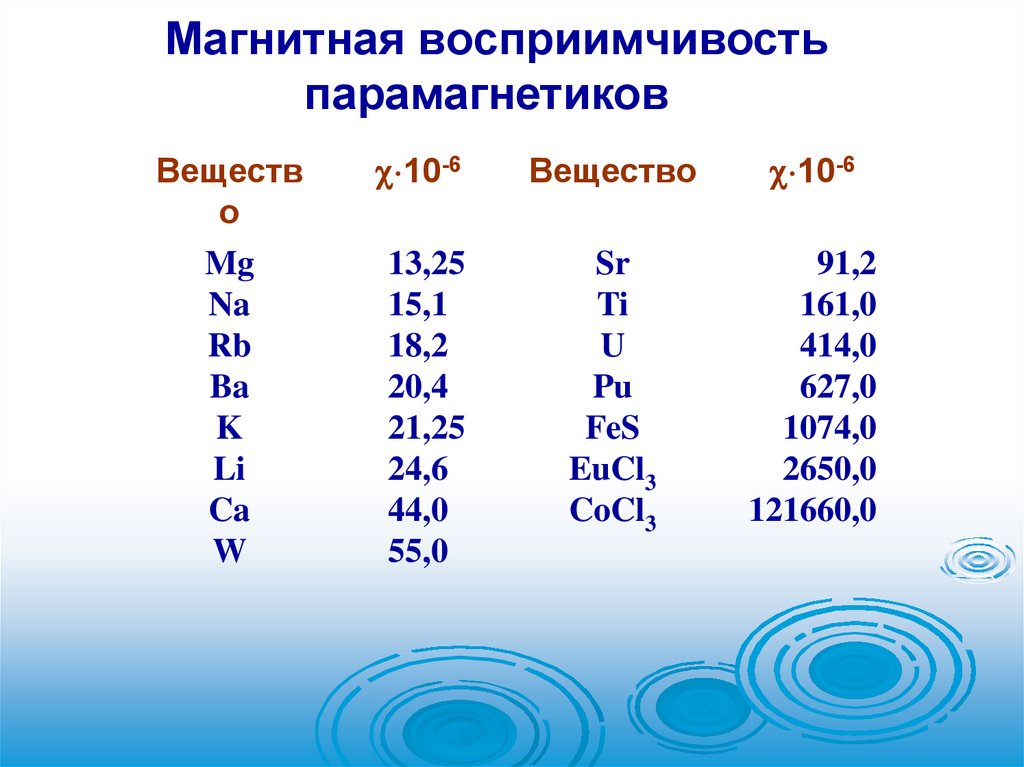
66.

Магнитная восприимчивость
парамагнетиков
Веществ
о
Mg
Na
Rb
Ba
K
Li
Ca
W
10-6
Вещество
10-6
13,25
15,1
18,2
20,4
21,25
24,6
44,0
55,0
Sr
Ti
U
Pu
FeS
EuCl3
CoCl3
91,2
161,0
414,0
627,0
1074,0
2650,0
121660,0

67.

ДИАМАГНЕТИК В МАГНИТНОМ ПОЛЕ
B0 0
B0 0
pa 0
Магнитные моменты
молекул равны нулю
Индуцируются незатухающие
молекулярные
токи,
поле
которых,
согласно
правилу
Ленца, ослабляет внешнее поле

68.

Магнитная восприимчивость
диамагнетиков
Вещество
10-6
He
Cu
Zn
Ag
Au
Bi
CO2
2,02
5,41
11,40
21,50
29,59
284,0
21

69.

Диамагнитный эффект присущ всем веществам и не
зависит от температуры.
Парамагнитный эффект зависит от температуры, т.к.
тепловое движение атомов и молекул разрушает ориентацию
их магнитных моментов во внешнем магнитном поле.
Зависимость магнитной восприимчивости парамагнетика
от температуры
C
m
T
закон
Кюри
При низких температурах наблюдается отклонение от
закона Кюри.

70.

ФЕРРОМАГНЕТИКИ
Сильномагнитные вещества — ферромагнетики — вещества,
обладающие спонтанной намагниченностью, т. е. они
намагничены даже при отсутствии внешнего магнитного поля. К
ферромагнетикам кроме железа относятся, кобальт, никель,
гадолиний, их сплавы и соединения.
https://avatars.mds.yandex.net/get-imagescbir/101700/b3QpDqIrYrD1mZVdzIQf_w2232/ocr
Области
спонтанной
намагниченности - домены

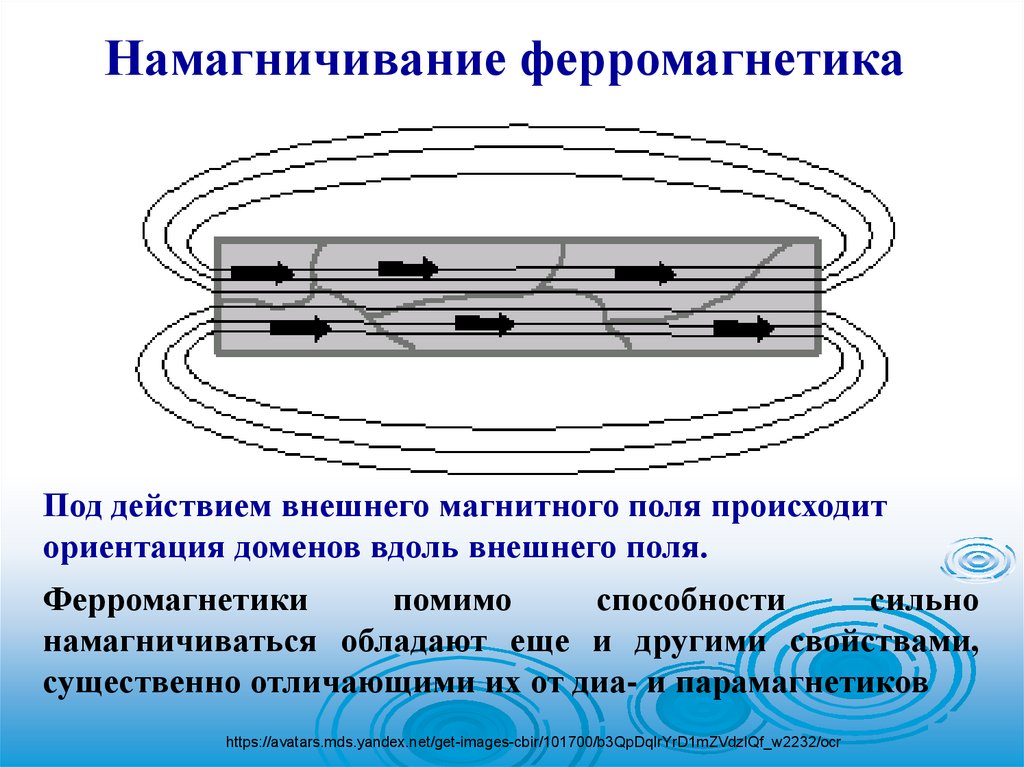
71.

Намагничивание ферромагнетика
Под действием внешнего магнитного поля происходит
ориентация доменов вдоль внешнего поля.
Ферромагнетики
помимо
способности
сильно
намагничиваться обладают еще и другими свойствами,
существенно отличающими их от диа- и парамагнетиков
https://avatars.mds.yandex.net/get-images-cbir/101700/b3QpDqIrYrD1mZVdzIQf_w2232/ocr

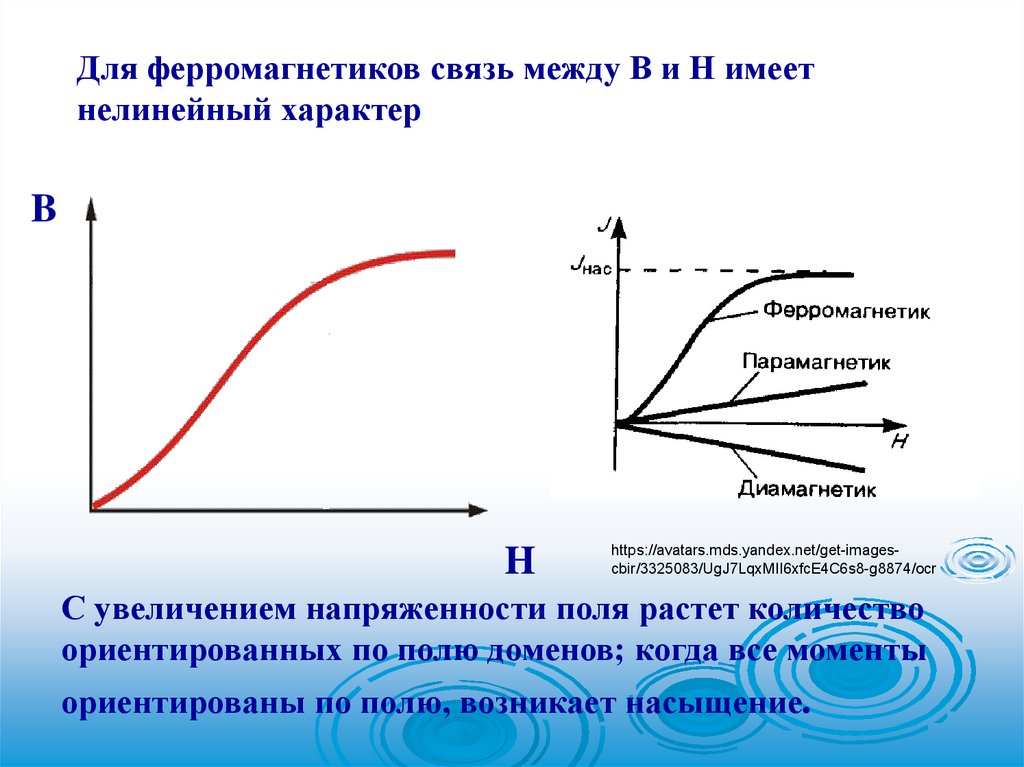
72.

Для ферромагнетиков связь между В и Н имеет
нелинейный характер
B
H
https://avatars.mds.yandex.net/get-imagescbir/3325083/UgJ7LqxMII6xfcE4C6s8-g8874/ocr
С увеличением напряженности поля растет количество
ориентированных по полю доменов; когда все моменты
ориентированы по полю, возникает насыщение.

73.

Магнитная проницаемость ферромагнетиков зависит от
внешнего поля
H
Существенная особенность ферромагнетиков — не только
большие значения ), но и зависимость от Н. Вначале
растет с увеличением Н, затем, достигая максимума, начинает
уменьшаться, стремясь в случае сильных полей к 1

74.

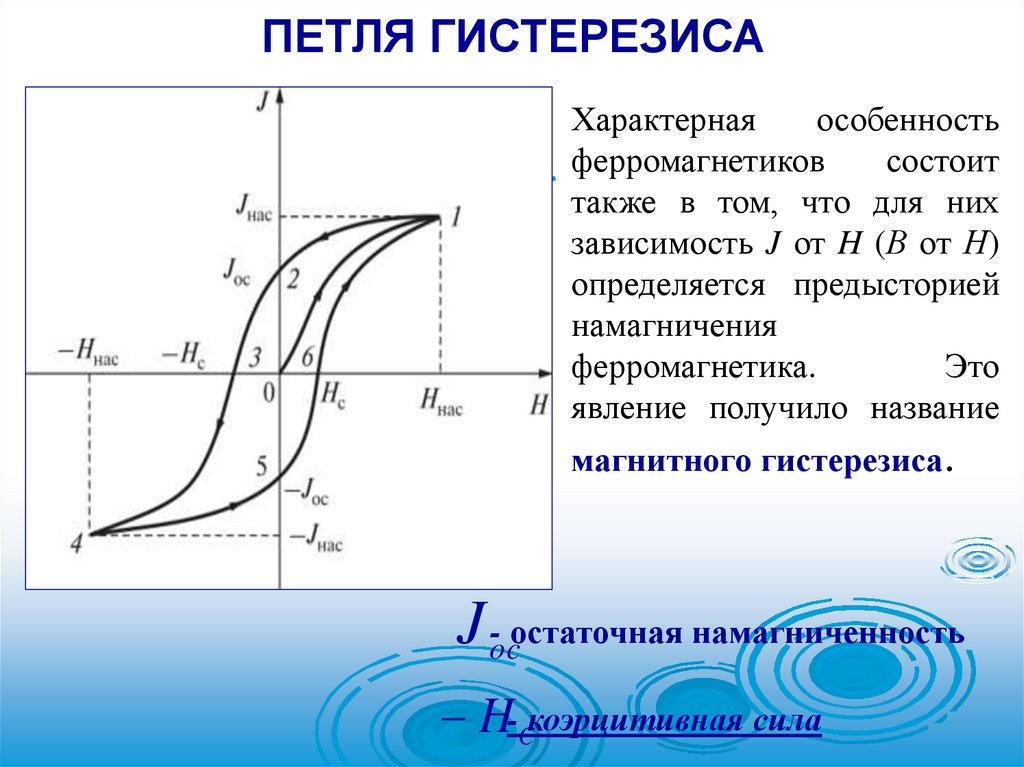
ПЕТЛЯ ГИСТЕРЕЗИСА
J
J нас
J oc
HC
Характерная
особенность
ферромагнетиков
состоит
также в том, что для них
зависимость J от H (В от Н)
определяется предысторией
намагничения
ферромагнетика.
Это
явление получило название
магнитного гистерезиса.
J oc- остаточная намагниченность
H-Cкоэрцитивная сила

75.

Температура Кюри ферромагнетиков
При
высоких
температурах
ферромагнетик
превращается в парамагнетик, поскольку доменная
структура
вещества разрушается
под действием
теплового движения. Температура, при которой
ферромагнетик
превращается
в
парамагнетик,
называется точкой Кюри
Материал
Железо
Кобальт
Никель
Температура
Кюри, К
1043
1393
631

76.

ДОМЕНЫ

77.

МАГНИТНЫЕ ОБОИ
Коснувшись
одного цветка на
обоях, вы
можете
включить лампу,
другой запустит
музыкальный
Фото с сайта
http://hlt.media.mit.edu/living_wall/index.html
диск, третий
управляет
Фокус внутри самих тонких обоев.
тостером,
Исследователи проложили фольгу
из стали
четвертый
между слоями бумаги, покрытой магнитной

78.

Спасибо за внимание

79.

Уравнения максвелла
По Максвеллу, изменяющееся во времени магнитное поле
порождает электрическое поле ЕB, циркуляция которого
Ed t
BdS
B
BdS dS
t
t
Циркуляция вектора напряженности суммарного эл. поля
B
Ed t dS
Это уравнение показывает, что источниками электрического
поля могут быть не только электрические заряды, но и
изменяющиеся во времени магнитные поля.

80.

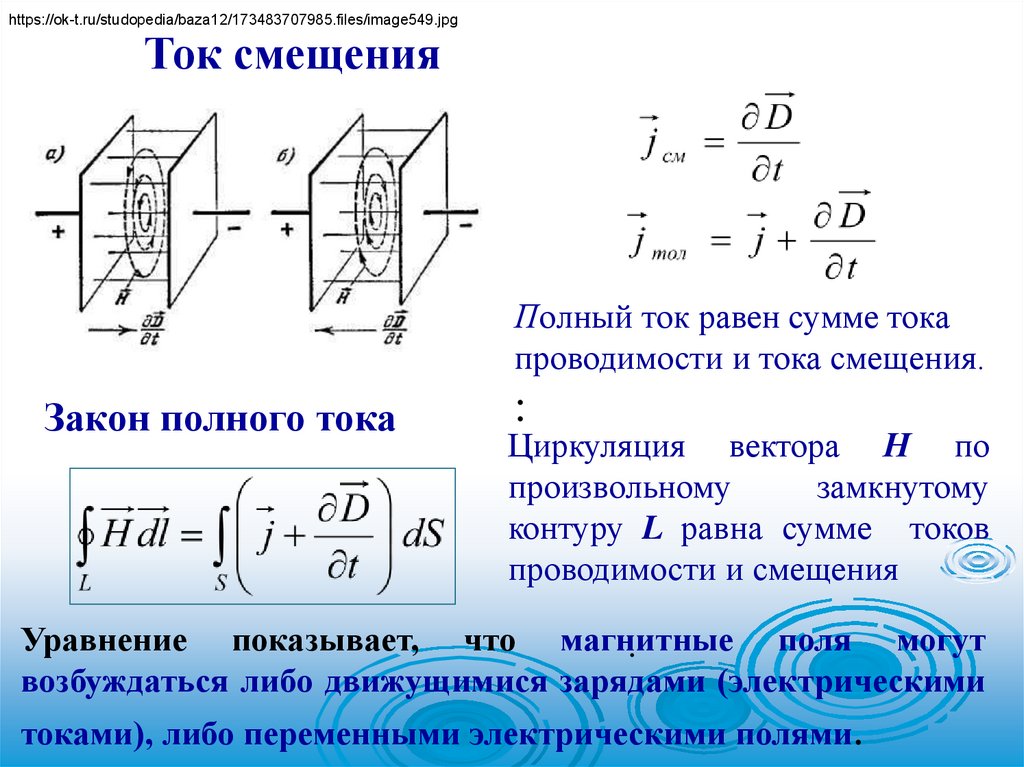
https://ok-t.ru/studopedia/baza12/173483707985.files/image549.jpg
Ток смещения
Полный ток равен сумме тока
проводимости и тока смещения.
Закон полного тока
:
Циркуляция вектора Н по
произвольному
замкнутому
контуру L равна сумме токов
проводимости и смещения
Уравнение показывает, что магнитные
поля могут
.
возбуждаться либо движущимися зарядами (электрическими
токами), либо переменными электрическими полями.

81.

Третье уравнение Максвелла для электромагнитного
поля — теорема Гаусса для поля D
Если заряд распределен внутри замкнутой поверхности
непрерывно с объемной плотностью ,
Четвертое уравнение Максвелла для электромагнитного
поля — теорема Гаусса для поля В

82.

Уравнения Максвелла в интегральной форме
Величины, входящие в уравнения Максвелла, не являются
независимыми и между ними существует следующая связь
(изотропные несегнетоэлектрические и неферромагнитные
среды):

83.

Уравнения Максвелла в интегральной форме
Из уравнений Максвелла следует, что переменное магнитное
поле всегда связано с порождаемым им электрическим полем,
а переменное электрическое поле всегда связано с
порождаемым им магнитным, т. е. электрическое и магнитное
поля неразрывно связаны друг с другом — они образуют единое
электромагнитное поле.
Теория Максвелла - обобщение основных законов
электрических и магнитных явлений, не только смогла объяснить
уже известные экспериментальные факты, но и предсказала новые
явления.
Одним из важных выводов этой теории явилось существование
магнитного поля токов смещения, что позволило Максвеллу
предсказать существование электромагнитных волн —
переменного электромагнитного поля, распространяющегося в
пространстве с конечной скоростью.