Похожие презентации:
Bohr Postulates (Lecture 8)
1.
Physics 2Voronkov Vladimir Vasilyevich
2. Lecture 8
• Bohr postulates• The Bohr model of hydrogen
• The true spectrum of hydrogen
• The spin of electron
3. Bohr Postulates
Bohr postulated:1. An electron in an atom can move around the nucleus
in certain circular stable orbits, without emitting
radiation.
There is a definite discrete energy associated with
each stable orbit.
2. The magnitude of the electron’s angular momentum
is quantized:
L = mvr = nћ , where n = 1,2,3,……
Each value of n corresponds to permitted value of the
orbit radius rn, and speed vn.
n is the principal quantum number for the orbit.
4.
3. An electron radiates energy only when itmakes a transition from one of its discrete orbit
with ni to another lower orbit nf: ni << nf.
The energy is radiated in the form of a photon
with energy and frequency, given by equation:
hf = Ei – Ef.
(note: ћ ≡ h/(2p) )
The Bohr postulates are aimed at resolving
difficulties of the Rutherford model of the
atom.
5. Bohr Model of Hydrogen
• The hydrogen atom consists of:– one electron of mass me and charge -e,
– a nucleus that usually consists of a single
proton, of mass mp >> me and charge +e.
• The classical model of configuration is
planetary: the electron in circular (or
elliptical) orbits with the proton at the
center (or a focus), in analogy to
planetary orbits.
6.
For a circular orbit of radius r, Newton'ssecond law is
From what we get
7.
The total mechanical energy for an electron onan orbit is
Here we choose that U(r= )=0.
And finally we find
8.
Using Bohr postulates we can find the radii ofelectron orbits:
a0=0.53*10-10m is the Bohr radius.
This formula is for allowed radii of electron
orbits in the hydrogen atom.
9.
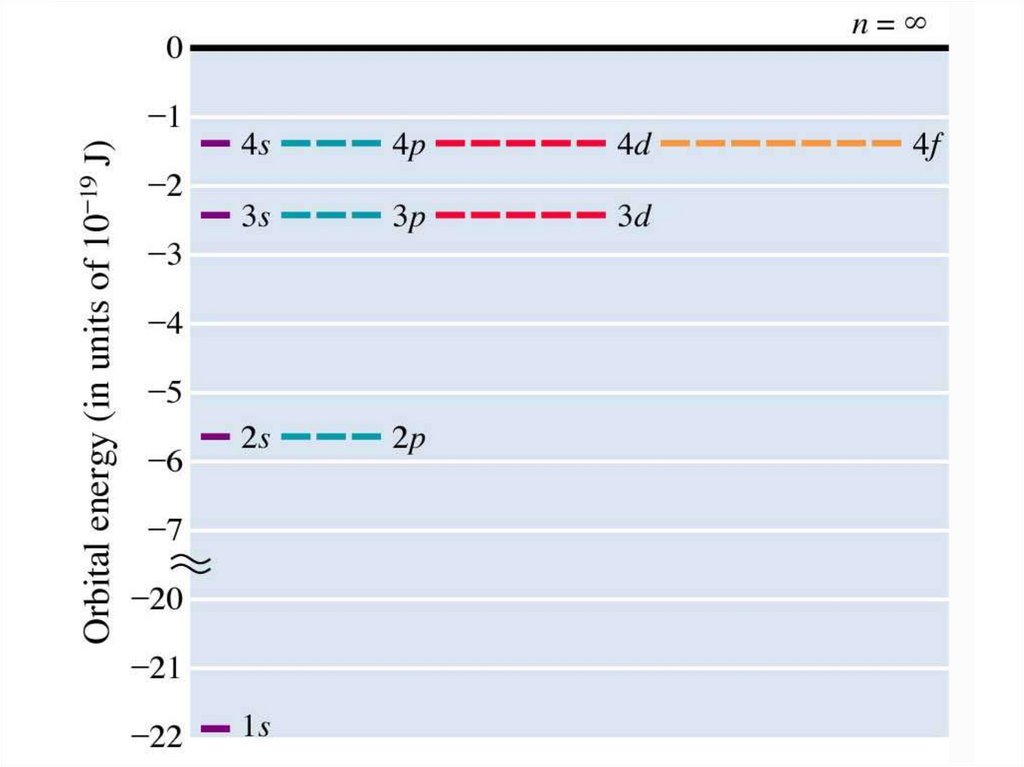
The ground-state energy (n=1) of electron inhydrogen atom is -13.6 eV.
10.
The energy levels ina hydrogen atom for
circular orbits in the
Bohr model. The
energy levels bunch up
as the quantum number
n increases. Above the
ionization point E = 0,
the electron and the
proton are no longer
bound together.
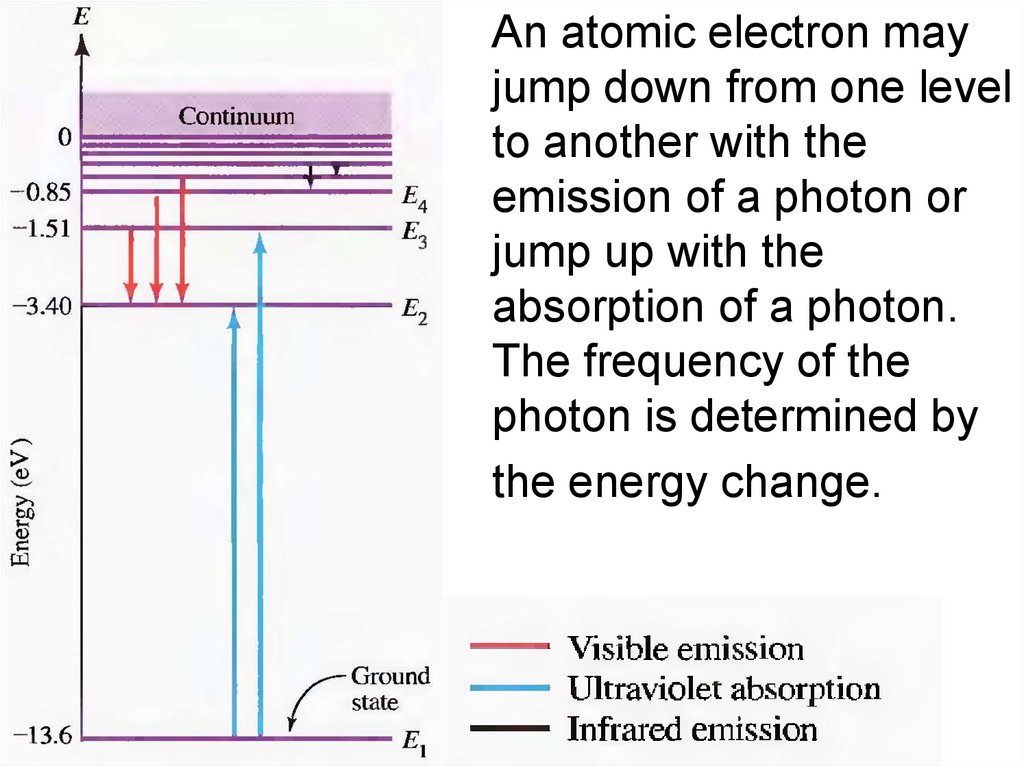
11.
An atomic electron mayjump down from one level
to another with the
emission of a photon or
jump up with the
absorption of a photon.
The frequency of the
photon is determined by
the energy change.
12.
The wavelengths of the photons emitted whenan electron jumps down from an initial excited
state to a lower-energy final state (Ei > Er) are
restricted to
ni and are the quantum numbers of the initial
and final states
= 1.09677576*107 1/m
is the Rydberg constant.
13. Bohr Correspondence Principle
Bohrcorrespondence
principle states that quantum
mechanical results should
reduce to those that follow
from a classical treatment
when quantum numbers are
large.
For example when the
principal atomic quantum
number n is large, the energy
levels are not so discrete as for
small values of n.
14. The True Spectrum of Hydrogen
• The square of the electron’s angularmomentum takes on discrete values, with
L2 taking on the values l(l + 1)ћ2, where
l= 0,1,2,3,... n-1
• In addition, only one component of
angular momentum, along a definite but
arbitrary axis (which we shall call the zaxis), can be specified, and for a given
value of l it can only take on the values
mћ, with the following meanings of m:
m = -l, -l+1, -l+2, . . . -1, 0, 1, . . . l-1, l.
So the z-component Lz of the angular
momentum vector is itself quantized.
• This behavior is totally at variance with
classical mechanics, although for very
large L, the deviations from the classical
description are negligibly small.
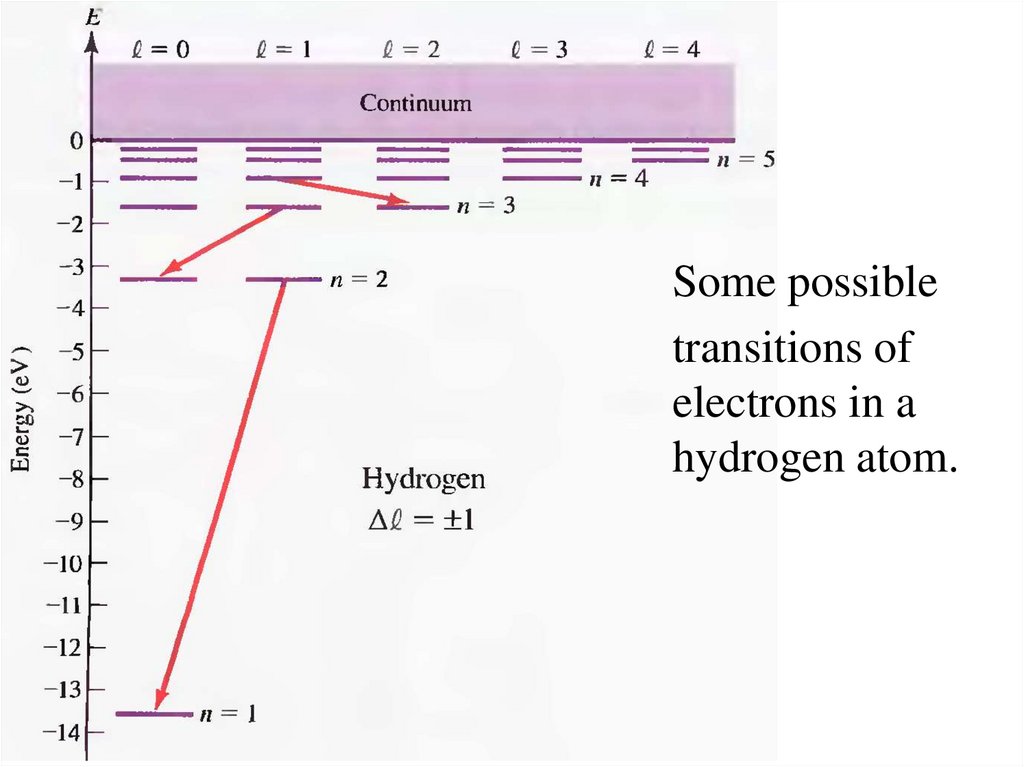
15.
Some possibletransitions of
electrons in a
hydrogen atom.
16.
The spectrum is limitedby the constraint of
angular momentum
conservation. The
angular momentum of a
photon is Lphoton = ћ. So,
the initial and final
angular momenta of the
electron states must
differ by one unit of , ћ:
Dl = 1
17. The Spin of the Electron
When an atom with a magnetic dipole moment is placed in anexternal magnetic field, it has a potential energy
Umag = -mB.
m is magnetic dipole moment of the atom due to orbital
rotation of the electron
B is the external magnetic field
Each one of the 2l + 1 orientations of an atom with angular
momentum quantum number l has a magnetic dipole moment
with a different z-component. If hydrogen is placed in an
external magnetic field, the energies of the first excited state
with l = 1 are therefore slightly split. The frequencies of the
radiation emitted (or absorbed) in a transition to or from one of
the three (now split) levels are accordingly not quite the same,
and experiment confirms it.
18.
When a hydrogen atom is subject to an external magneticfield, the three states corresponding to l=1, which all
have the same energy in no magnetic field, have slightly
different energies-the levels are split. The amount of
splitting depends on the strength of the magnetic field.
Note that the l = 0 state consists of only one level and is
therefore not split.
19.
States of a given l that have a common energy in theabsence of a magnetic field break up into (2l + 1)member multiplets with slightly different energies in
the presence of a magnetic field. Because l= 0,
1,2,3,… only odd-valued multiplets were expected.
But experiment showed even number of multiplets in
some cases. So for duplets l must be: ½! This
phenomena was explained that the electron has an
intrinsic angular momentum, or spin sћ, and
s=±½.
This means that an electron at rest still has its
intrinsic angular momentum sћ.
20.
• s=1/2 means that 2s + 1 = 2, thus an electron canappear in two states. These states are called "up"
and "down."
• In the absence of a magnetic field, the energy of
an "up" electron is the same as that of a "down"
electron in the hydrogen atom.
• However, when a magnetic field is present, the
energies of these two states differ slightly. When
the electrons jump from these two states, the
frequencies of the photons emitted differ slightly.
As a result of electron spin, the number of
possible electron states that correspond to a given
l doubles from 2l + 1 to 2(2l + 1).
21.
The existence of electron spin explains whysome states are split into an even number of
levels when a magnetic field is applied.
22.
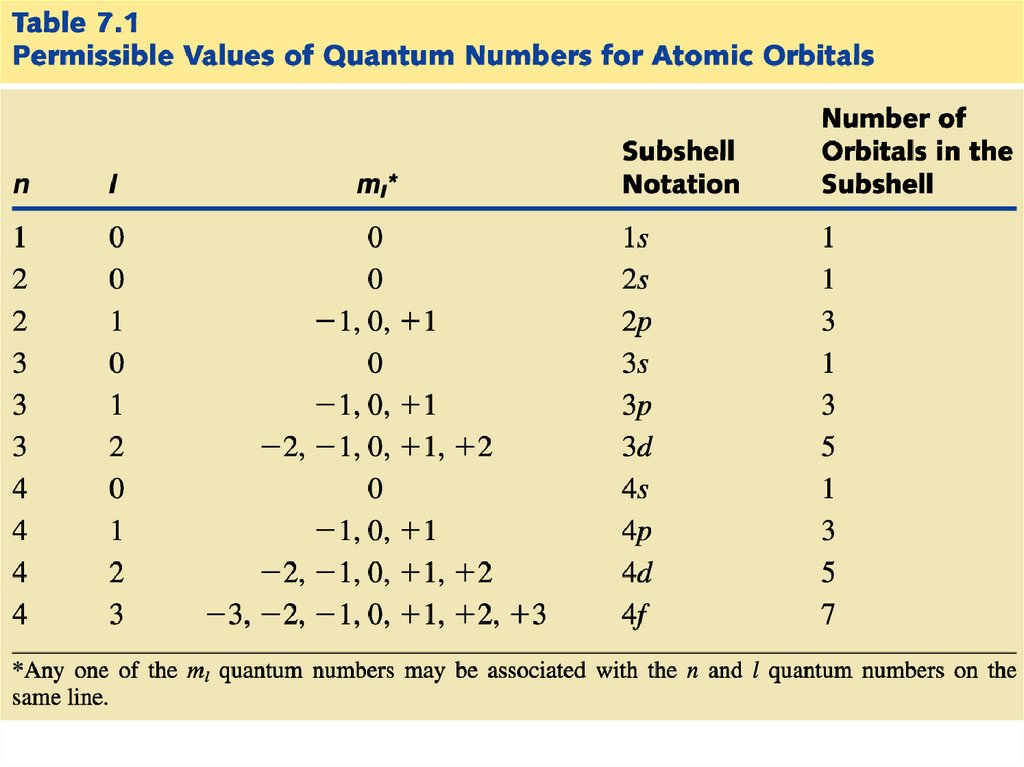
Each electron is described by fourquantum numbers:
n - principal quantum number
l - angular momentum quantum number
ml - magnetic quantum number
ms - spin quantum number
The first three define the wave function for a
particular electron. The fourth quantum
number refers to the magnetic property of
electrons.
23.
The principal quantum number (n)represents the “shell number” in
which an electron “resides.”
The smaller n is, the smaller the orbital.
The smaller n is, the lower the energy of
the electron.
n tells us the size of the orbital and the
energy of the orbital
The allowed values of n are 1, 2, 3, 4…
(integers)
24.
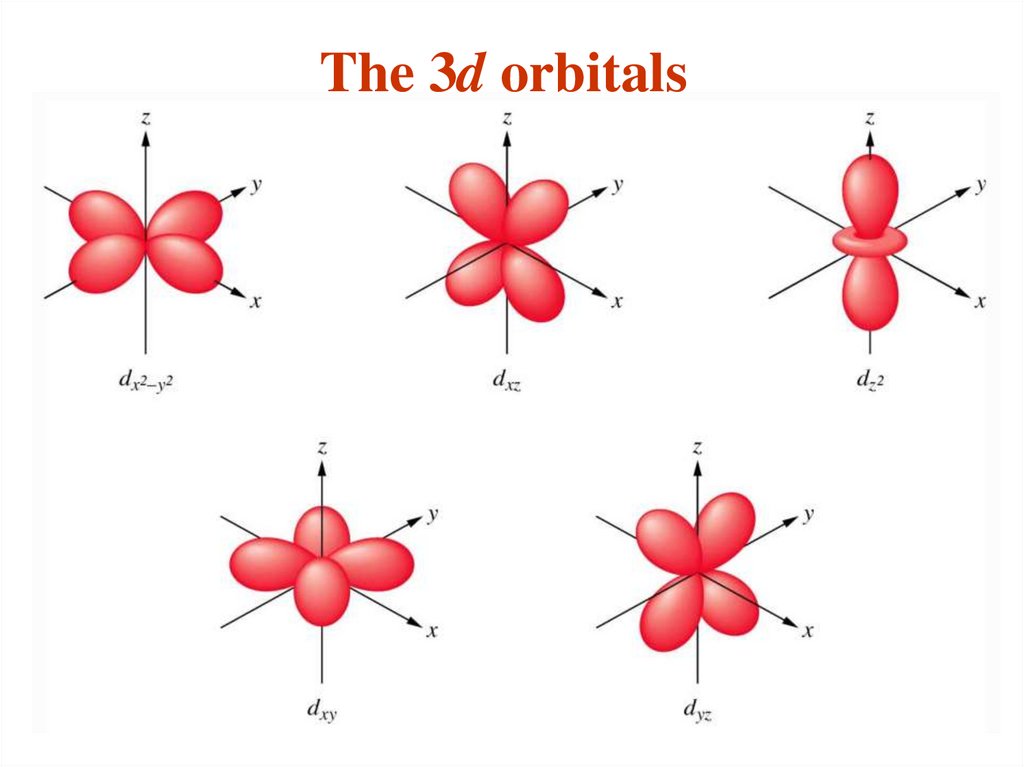
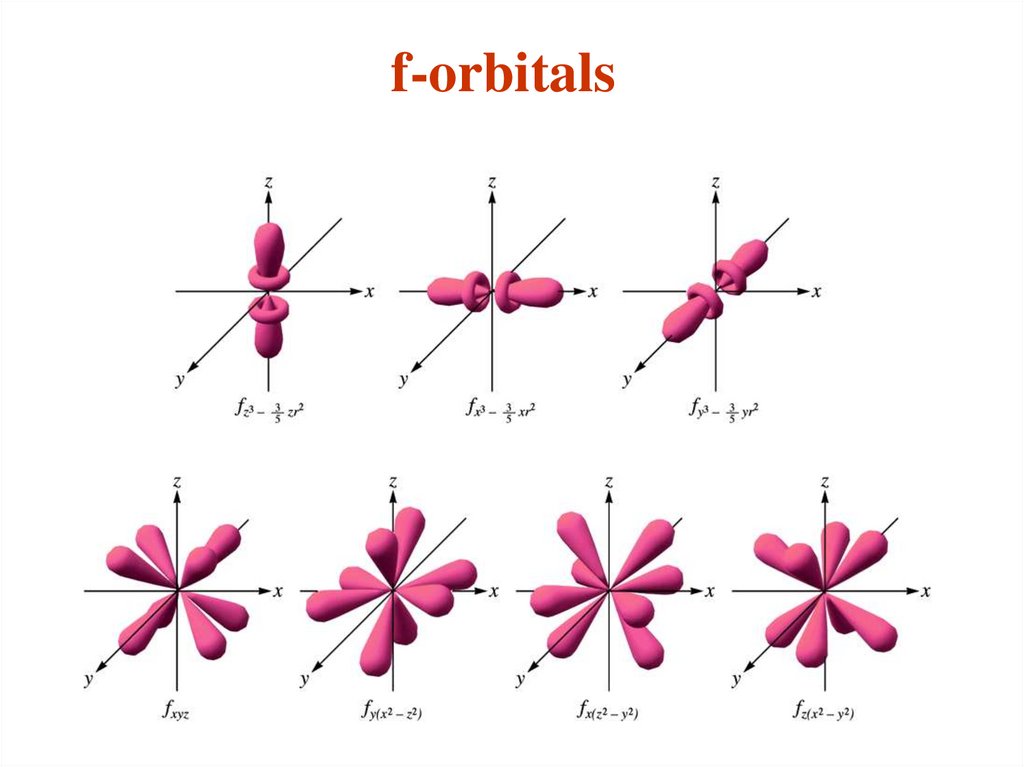
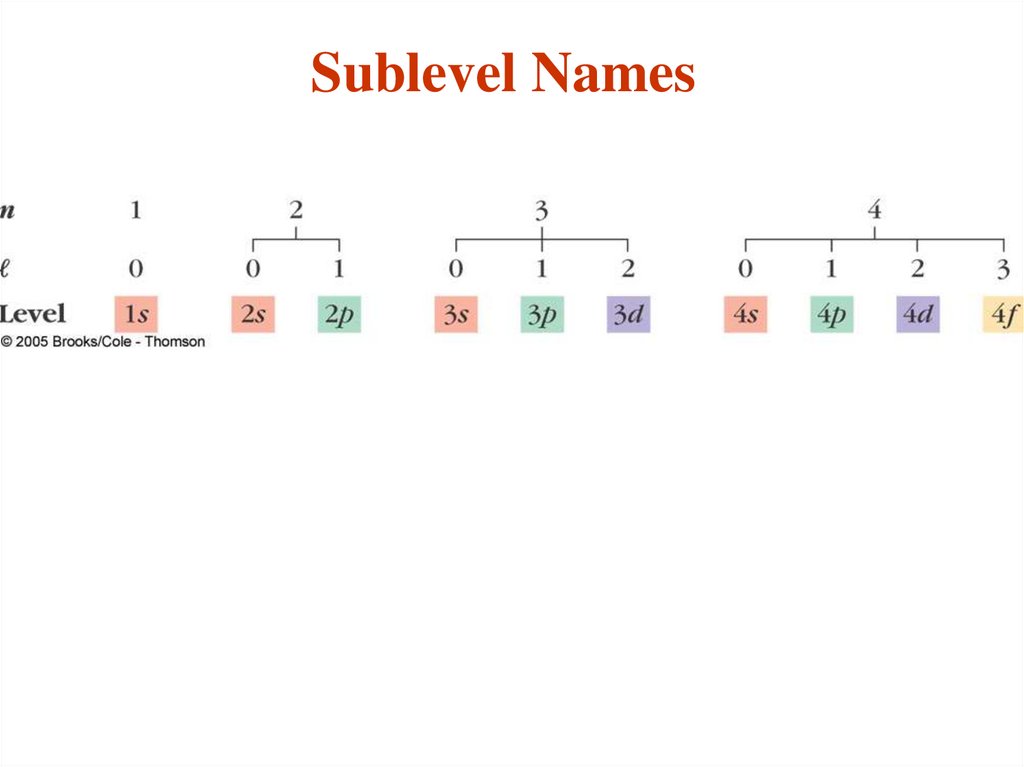
The angular momentum quantum number (l)distinguishes “sub shells” within a given shell
that have different shapes.
- Each main “shell” is subdivided into “sub shells.”
Within each shell of quantum number n, there are n
sub shells, each with a distinctive shape.
- l can have any integer value from 0 to (n - 1)
The different sub-shells are denoted by letters.
Letter
s p d f g …
l
0 1 2 3 4 ….
25.
The hydrogenelectron orbitals
- black=zero density,
- white=highest
density).
- Brighter areas
correspond to higher
probability density for a
position measurement
• Probability densities for
a wavefunctions of an
electron in a hydrogen
atom possessing
definite energy n = 1,
2, 3, ...) and angular s,
p, d,...) and magnetic
momentum: m=0
26.
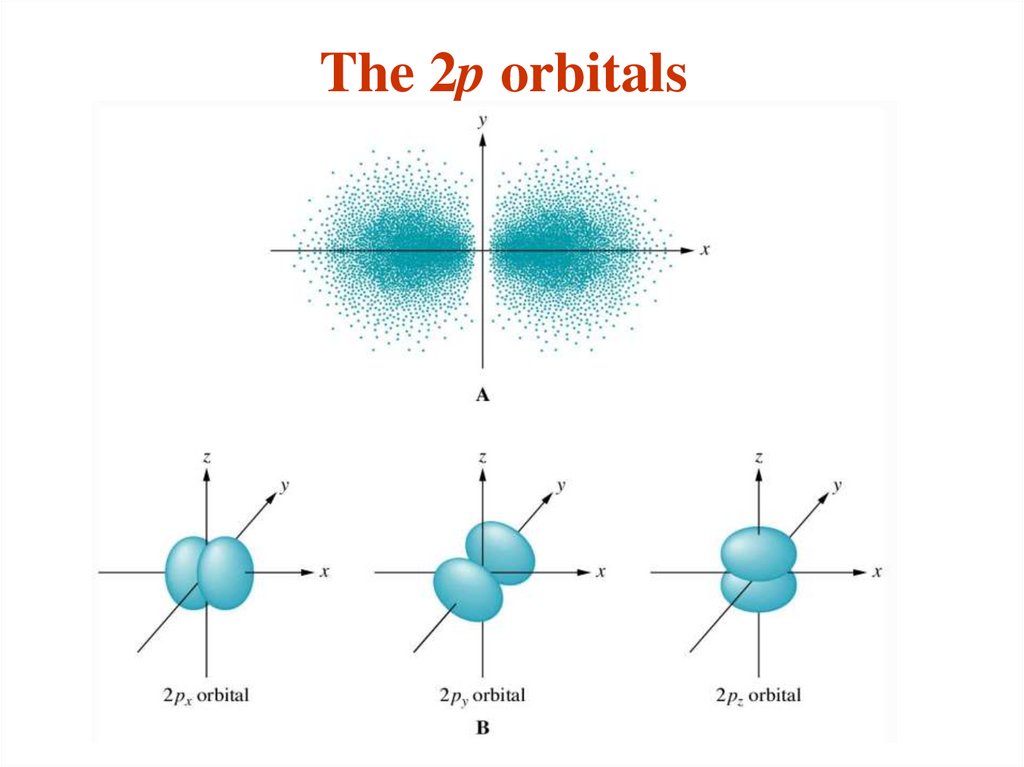
The magnetic quantum number (ml)distinguishes orbitals within a given subshell that have different shapes and
orientations in space.
• Each sub shell is subdivided into “orbitals,”
• each capable of holding a pair of electrons.
ml can have any integer value from -l to +l.
• Each orbital within a given sub shell has the
same energy.
27.
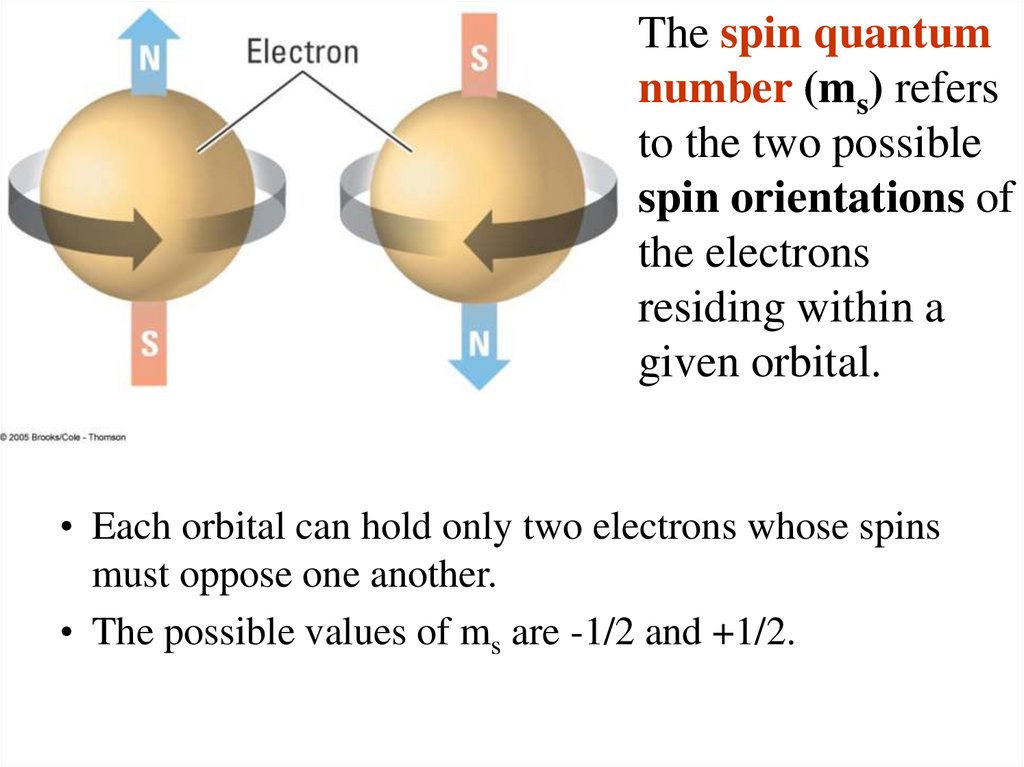
The spin quantumnumber (ms) refers
to the two possible
spin orientations of
the electrons
residing within a
given orbital.
• Each orbital can hold only two electrons whose spins
must oppose one another.
• The possible values of ms are -1/2 and +1/2.
28.
29.
30.
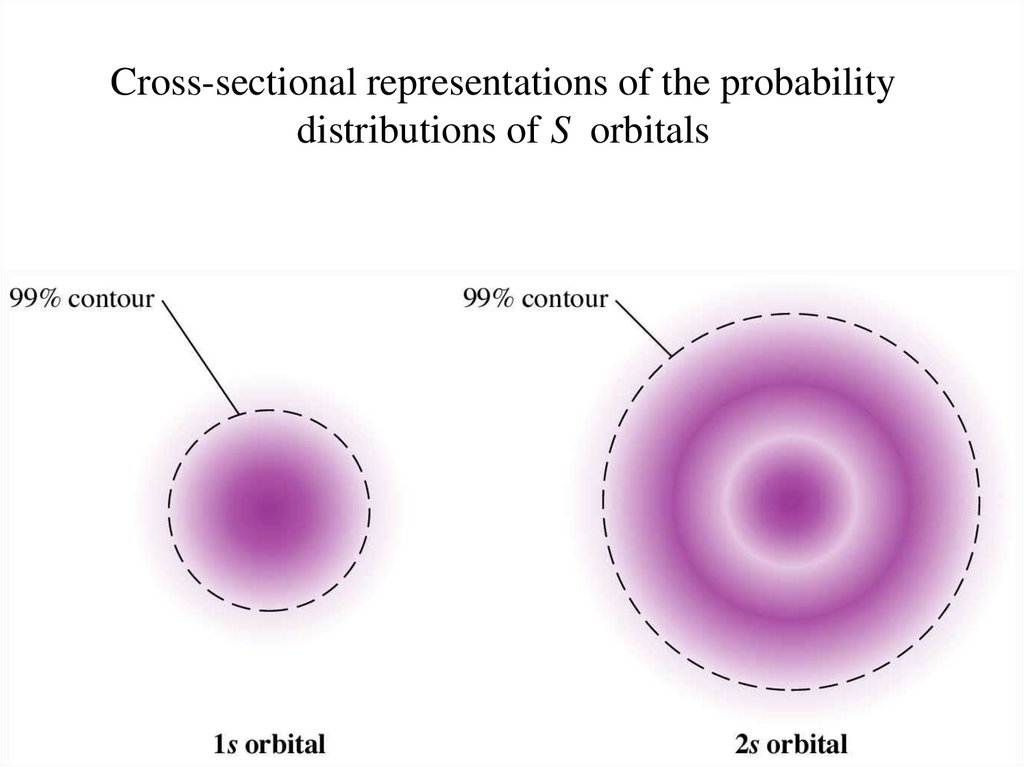
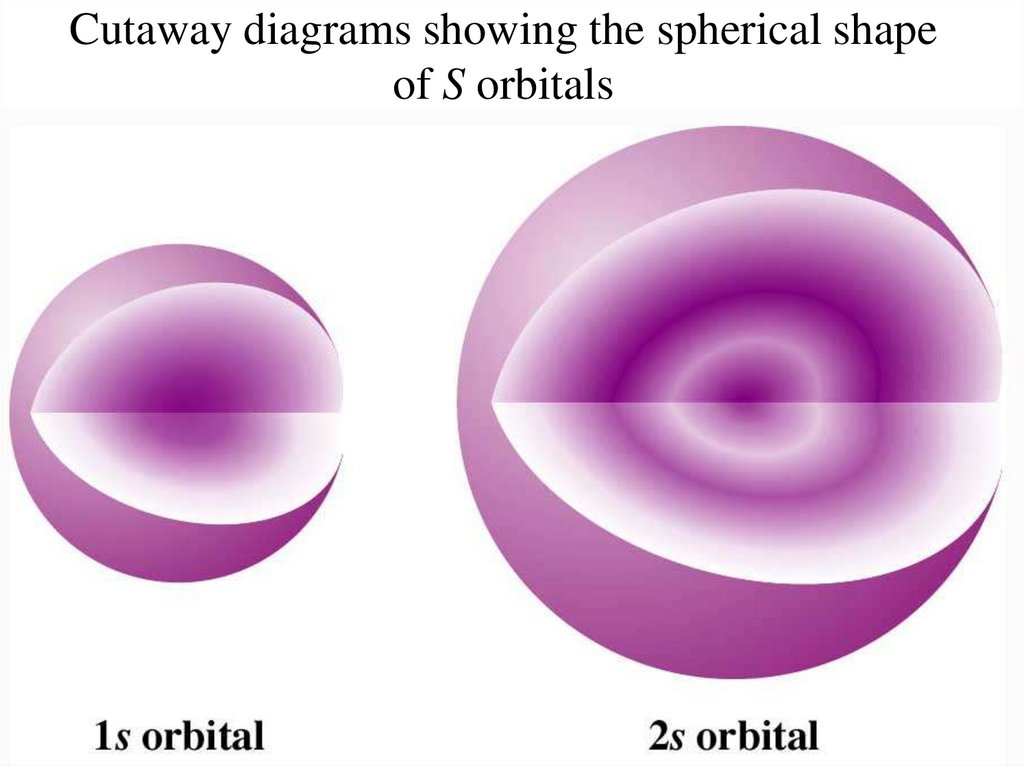
Cross-sectional representations of the probabilitydistributions of S orbitals
























 Физика
Физика








