10. Некоторые элементарные функции_595c96c4-7cb8-4d78-8def-341e8beca167

1.

Васильева Ольга Валерьевна
Некоторые элементарные функции

2.

Зачем это учить?
Для анализа эффективности алгоритмов используется такие понятия как
асимптотическая оценка и нотация («О-большое», «Ω-большая» и «ϴбольшая»). В этой теме мы кратко обсудим некоторые свойства графиков
вещественных функций действительной переменной, необходимые для
понимания этих параметров.

3.

Система координат
Система координат на плоскости — это прямоугольная
(декартова) система координат.
Она задаётся двумя взаимно перпендикулярными
прямыми — осями, на каждой из которых выбрано
положительное направление и задан единичный
(масштабный) отрезок. Эти оси называют осями координат,
точку их пересечения О — началом координат.
Одну из осей называют осью абсцисс (осью Ox), другую —
осью ординат (осью Oy).
Систему координат обозначают Oxy, а плоскость, в которой
расположена система координат, называют координатной
плоскостью.

4.

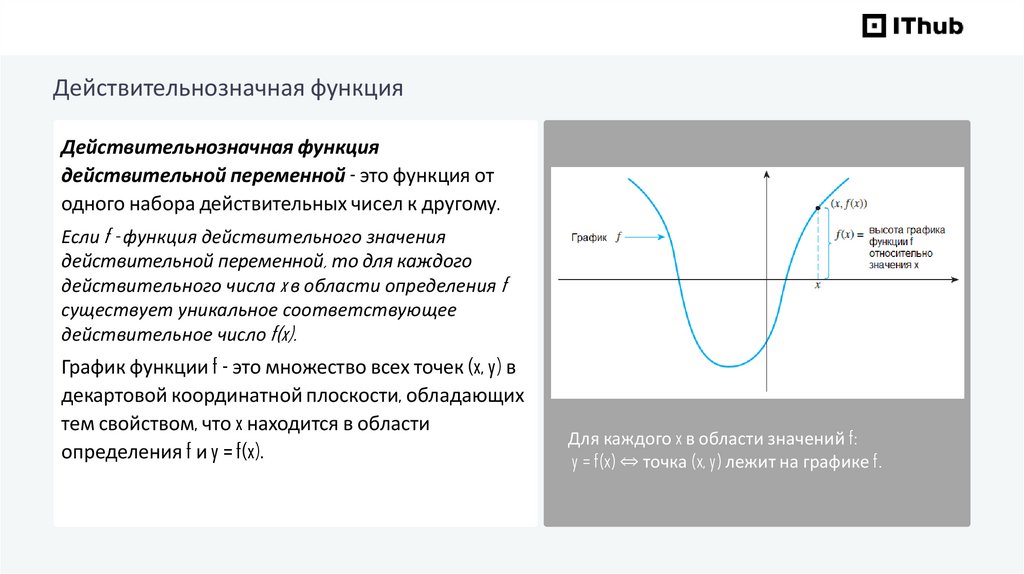
Действительнозначная функция
Действительнозначная функция
действительной переменной - это функция от
одного набора действительных чисел к другому.
Если f - функция действительного значения
действительной переменной, то для каждого
действительного числа x в области определения f
существует уникальное соответствующее
действительное число f(x).
График функции f - это множество всех точек (x, y) в
декартовой координатной плоскости, обладающих
тем свойством, что x находится в области
определения f и y = f(x).
Для каждого x в области значений f:
y = f(x) ⇔ точка (x, y) лежит на графике f.

5.

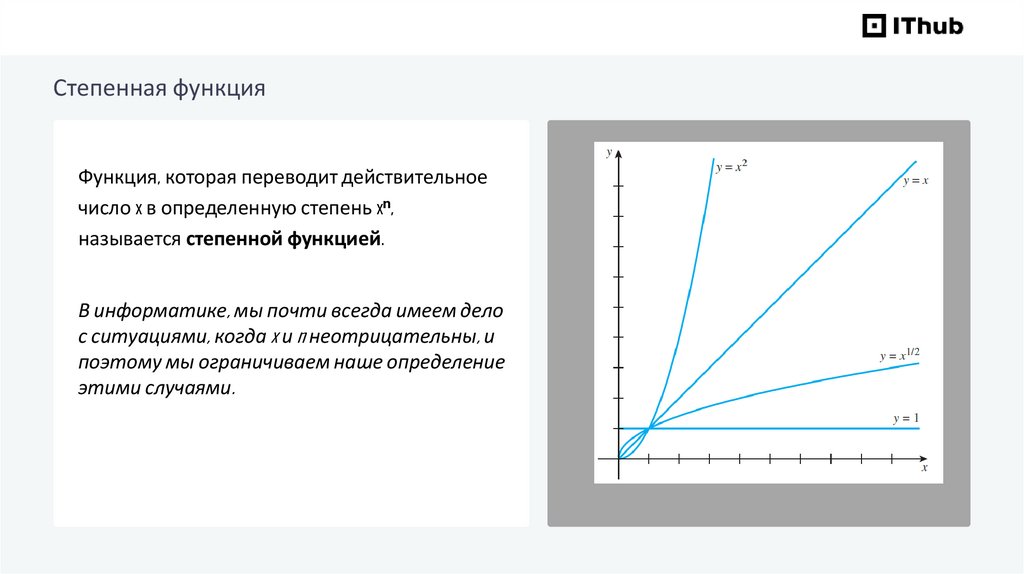
Степенная функция
Функция, которая переводит действительное
число x в определенную степень xⁿ,
называется степенной функцией.
В информатике, мы почти всегда имеем дело
с ситуациями, когда x и n неотрицательны, и
поэтому мы ограничиваем наше определение
этими случаями.

6.

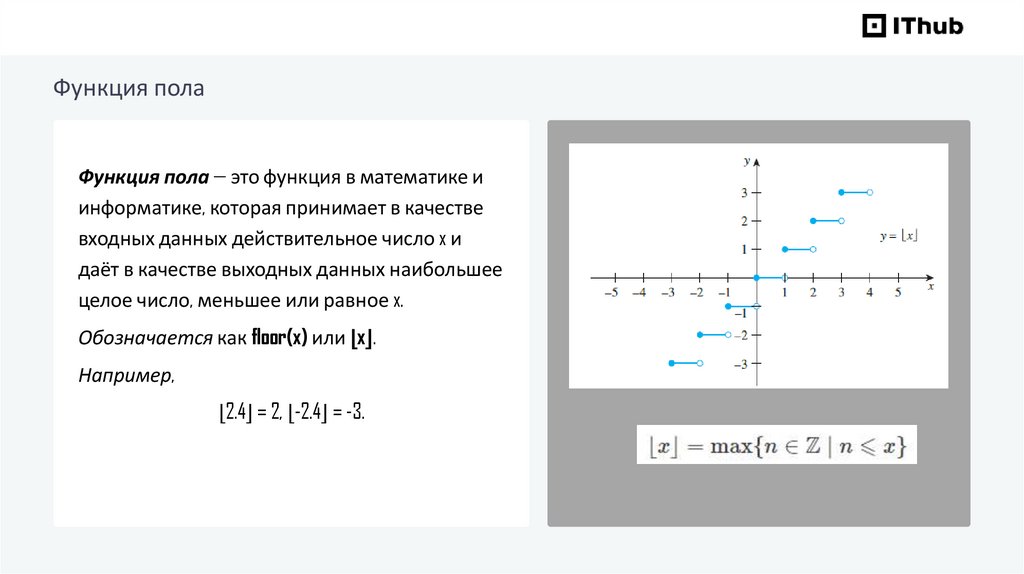
Функция пола
Функция пола — это функция в математике и
информатике, которая принимает в качестве
входных данных действительное число x и
даёт в качестве выходных данных наибольшее
целое число, меньшее или равное x.
Обозначается как floor(x) или ⌊x⌋.
Например,
⌊2.4⌋ = 2, ⌊-2.4⌋ = -3.

7.

Функция потолка
Функция потолка — это функция в
математике и информатике, которая
принимает в качестве входных данных
действительное число x и даёт в качестве
выходных данных в наименьшее целое число,
большее или равное x.
Обозначается как ⌈x⌉ или ceil(x).
Например,
⌈2.4⌉ = 3, ⌈-2.4⌉ = -2.

8.

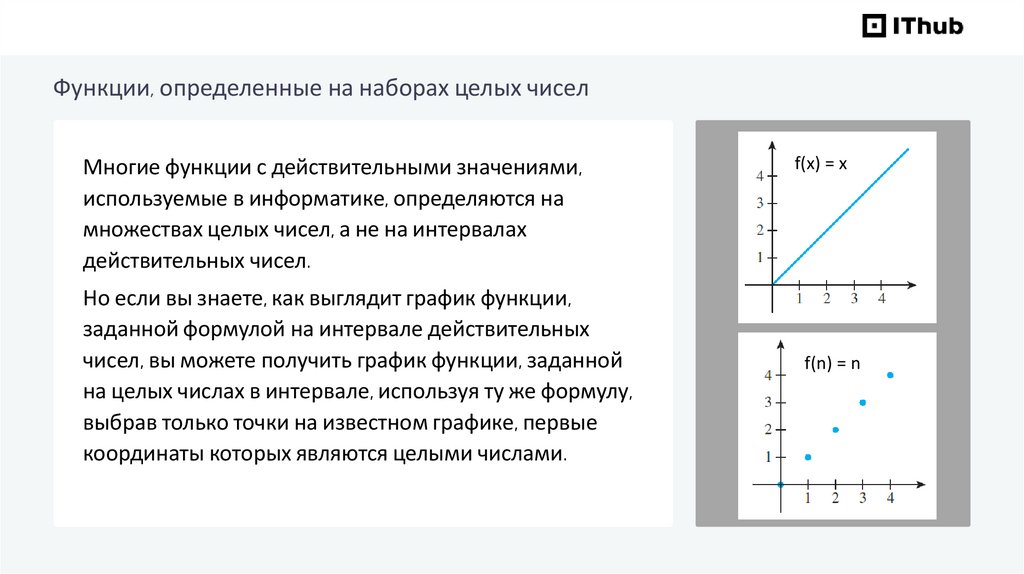
Функции, определенные на наборах целых чисел
Многие функции с действительными значениями,
используемые в информатике, определяются на
множествах целых чисел, а не на интервалах
действительных чисел.
Но если вы знаете, как выглядит график функции,
заданной формулой на интервале действительных
чисел, вы можете получить график функции, заданной
на целых числах в интервале, используя ту же формулу,
выбрав только точки на известном графике, первые
координаты которых являются целыми числами.
f(x) = x
f(n) = n

9.

Кратные функции
Кратность функции получается путем умножения каждого
значения функции на фиксированное число.
Пусть f - вещественная функция действительной
переменной, а M - любое действительное число.
Функция Mf , называемая кратной f на M или M,
умноженной на f, представляет собой
вещественнозначную функцию с той же областью
определения, что и f, которая определяется
правилом (Mf)(x) = M · (f(x)) для каждой x ∈ области
определения f.

10.

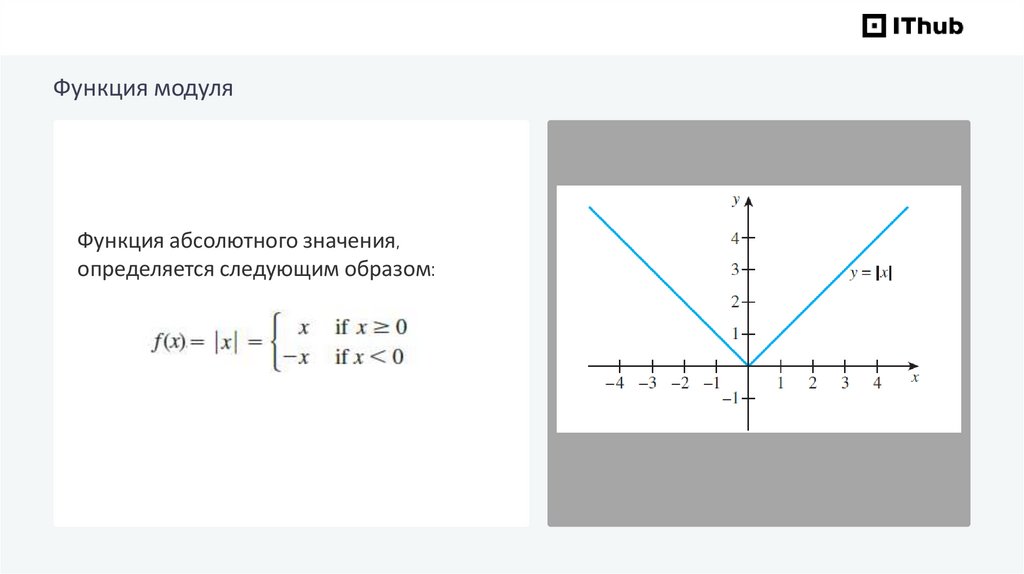
Функция модуля
Функция абсолютного значения,
определяется следующим образом:

11.

Возрастающие и убывающие функции
Пусть f — функция, определенная на множестве действительных
чисел, и предположим, что область определения f содержит
множество S.
Мы говорим, что f возрастает на множестве S тогда и только
тогда, когда для всех действительных чисел x₁ и x₂ в S, если x₁ < x₂,
то f (x₁) < f (x₂).
Мы говорим, что f убывает на множестве S тогда и только тогда,
когда для всех действительных чисел x₁ и x₂ в S, если x₁ < x₂, то f
(x₁) > f (х₂).
Мы говорим, что f является возрастающей (или
убывающей) функцией тогда и только тогда, когда f возрастает
(или убывает) на всей своей области определения.