Похожие презентации:
Простейшие функции и способы их задания, основные свойства. Лекция № 2
1.
2.
Понятиефункции
Обзор элементарных функций и их
графиков
3.
При изучении природных и технических процессовисследователи сталкиваются с величинами, которые мы
разделяем на переменные и постоянные.
Постоянной величиной называется величина,
сохраняющая одно и то же численное значение;
переменной величиной – величина, принимающая
различные численные значения.
В практических задачах изменение переменной величины
связано с изменением одной или нескольких других
переменных величин.
Переменная х называется независимой переменной или
аргументом функции. Переменная у называется
зависимой переменной или функцией. Чтобы задать
функцию y=f(x), необходимо указать правило,
позволяющее, зная х, находить соответствующее
значение у.
Наиболее часто встречаются три способа задания
функции: аналитический, табличный, графический.
4.
1. Аналитический способ: функция задаётся в виде одной илинескольких формул или уравнений.
Пример:
Если уравнение, с помощью которого задаётся функция, не
разрешено относительно у, то функция называется неявной.
Например, lg y 2 xy x 1.
2. Табличный способ: функция задаётся таблицей ряда
значений функции. Например, известные таблицы значений
тригонометрических функций.
На практике часто приходиться пользоваться таблицами значений
функций, полученных опытным путём или в результате
наблюдений.
3. Графический способ: задаётся график функции.
Графиком функции y=f(x) называется множество точек (х;у)
плоскости Оху, координаты которых связаны соотношением
y=f(x). Само равенство y=f(x) называется уравнением этого
графика.
Совокупность всех значений аргумента х, для которой функция
y=f(x)определена, называется областью определения этой
функции (обозначают D(f(x)) или D(у)). Совокупность всех
значений, принимаемых переменной у, называют областью
значений функции y=f(x)(Обозначают Е(f(x))или Е(у)).
5.
Пример1. Найти область определения функцииy 4 x2 .
Нам известно, что подкоренное выражение не может быть отрицательным. Запишем это в виде неравенства:
4 x 2 0.
Решением этого неравенства является отрезок [-2;2].
Запишем ответ:
D( y) [ 2;2].
Функция y = f(x)называется чётной (нечётной), если для каждого х из области определения функции число –х также
принадлежит её области определения и выполняется равенство
f(-x) = f(x) (f(-x) = -f(x)).
График чётной функции симметричен относительно оси ординат, а нечётной - относительно начала координат.
Пример 2. Какие из следующих функций - чётные, какие – нечётные, 1) y x cos x;
2) y x 2 cos x;
а какие не принадлежат ни одному из этих классов:
3) y x 2 x .
Решение:
1) y( x) x cos( x) x cos x ( x cos x) y( x);
y=x cosx
Следовательно, функция
4
y x cos x
2
0
нечётная
-6
-4
-2
и её график симметричен (как это видно из рисунка) относительно начала координат.
-6
чётная
и её график симметричен (как это видно из рисунка) относительно оси ординат.
y x 2
x
x y ( x) y ( x)
2
-4
0
-5 0
-2
2
4
6
-10
y=x*2^x
-15
200
150
100
x
ни четная, ни нечётная
6
5
y x cos x
Следовательно,
4
10
2
3) y ( x) x 2
2
-4
2
Следовательно, функция
x
0
y=x^2* cosx
2) y( x) ( x) cos( x) x cos x y( x);
2
-2
50
-6
-4
-2
0
-50 0
2
4
6
и её график не является симметричным ни относительно начала координат, ни относительно оси ординат.
Функция y=f(x)называется периодической, если существует такое число что для каждого х из области определения функции
значения х+Т и х-Т также принадлежат её области определения, и при этом выполняются равенства
f(x-T) = f(x) = f(x+T).
Число Т называется периодом функции y=f(x).
6.
Пример 3: Функция y=cos x является периодической с периодом5
Так как
y cos cos
y 0.
2
2
2
2
Функция y=f(x)называется возрастающей (убывающей), если для любых из области определения этой
функции и таких, что x1 x2 ,
выполняется неравенство
f ( x1 ) f ( x2 ) ( f ( x1 ) f ( x2 )).
Пример 4. Будет ли возрастающей (убывающей) функция:
1) y x 2 2 x 1,
x 1;
3
2) y .
Решение: x
1) Выберем два аргумента из области определения данной функции и вычислим значения функции в
рис.1
этих точках.
y (0) 0 2 2 0 1 1,
5
4
3
2
1
0
y (1) 12 2 1 1 4,
1 4 т.е. y (0) y (1).
-2
-1
0
1
2
3
Таким образом на своей области определения данная функция возрастает (см.рис.1).
2) Выберем два аргумента из области определения данной функции и вычислим значения функции в
3
рис.2
этих точках.
y (1) 3,
4
1
3
3
2
y (2) 1,5,
1
2
0
0
1
2
3
4
5
3 1,5 т.е. y (1) y (2).
Согласно определению данная функция убывает (см.рис.2).
4
7.
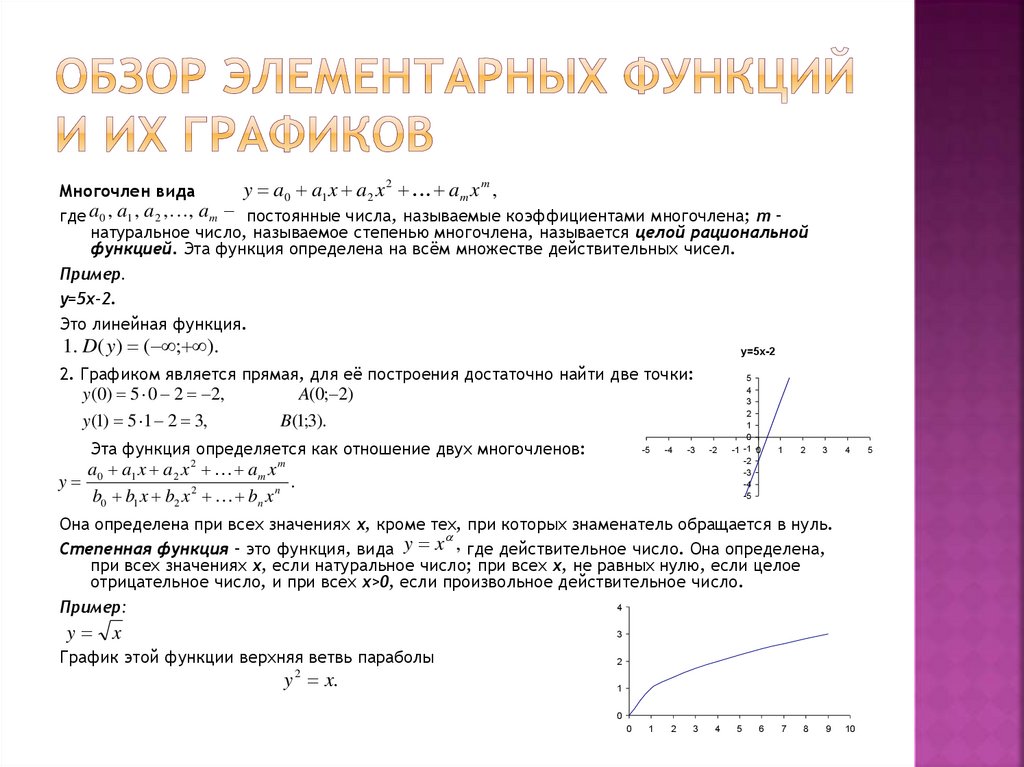
y a0 a1 x a2 x am x ,Многочлен вида
где a0 , a1 , a 2 , , a m постоянные числа, называемые коэффициентами многочлена; m –
натуральное число, называемое степенью многочлена, называется целой рациональной
функцией. Эта функция определена на всём множестве действительных чисел.
Пример.
у=5х-2.
Это линейная функция.
2
m
1. D( y) ( ; ).
y=5x-2
2. Графиком является прямая, для её построения достаточно найти две точки:
y (0) 5 0 2 2,
y (1) 5 1 2 3,
A(0; 2)
B(1;3).
Эта функция определяется как отношение двух многочленов:
y
-5
-4
-3
-2
a0 a1 x a2 x am x
.
b0 b1 x b2 x 2 bn x n
2
m
5
4
3
2
1
0
-1 -1 0
-2
-3
-4
-5
1
2
3
4
Она определена при всех значениях х, кроме тех, при которых знаменатель обращается в нуль.
Степенная функция – это функция, вида y x , где действительное число. Она определена,
при всех значениях х, если натуральное число; при всех х, не равных нулю, если целое
отрицательное число, и при всех х>0, если произвольное действительное число.
4
Пример:
y
x
3
График этой функции верхняя ветвь параболы
y x.
2
2
1
0
0
1
2
3
4
5
6
7
8
9
10
5
8.
а>10<a<1
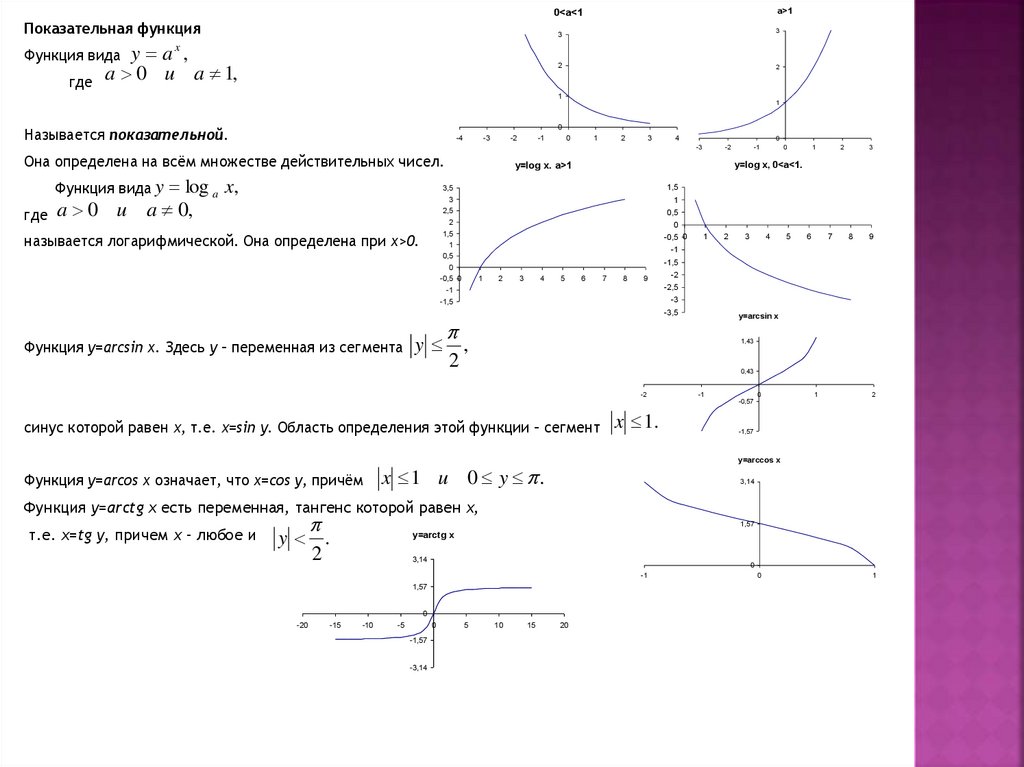
Показательная функция
y a ,
a 0 u a 1,
Функция вида
где
3
3
x
2
2
1
1
0
Называется показательной.
-4
-3
-2
-1
0
1
2
3
4
0
-3
Она определена на всём множестве действительных чисел.
log a x,
a 0,
Функция вида y
где
a 0 u
1
2,5
0,5
2
0
-0,5 0
1,5
1
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
-2
-3
-1,5
-3,5
y=arcsin x
,
1,43
0,43
-2
синус которой равен х, т.е. х=sin y. Область определения этой функции – сегмент
Функция y=arcos x означает, что x=cos y, причём
3
-2,5
-1
2
2
-1,5
0
-0,5 0
y
1
-1
0,5
Функция y=arcsin x. Здесь у – переменная из сегмента
0
1,5
3
-1
y=log x, 0<a<1.
y=log x. a>1
3,5
называется логарифмической. Она определена при x>0.
-2
x 1.
-1
-0,57
0
1
2
-1,57
y=arccos x
x 1 u 0 y .
3,14
Функция y=arctg x есть переменная, тангенс которой равен х,
т.е. x=tg y, причем х – любое и
1,57
y .
2
y=arctg x
3,14
0
-1
1,57
0
-20
-15
-10
-5
0
-1,57
-3,14
5
10
15
20
0
1
9.
Функция y=arcctg x есть переменная, для которой x=ctg y, где х – любое и 0 y .y=arctg x
6,28
4,71
3,14
1,57
0
-60
-40
-20
0
20
40
60
Пусть переменная у зависит от переменной и, которая в свою очередь зависит от
переменной х, т.е. y f (u), u ( x).
Тогда при изменении х будет меняться и и, а следовательно будет меняться и у. Значит у
является функцией х: y f ( ( x)).
Эта функция называется сложной функцией, переменная и называется промежуточной
переменой. Указанную сложную функцию называют также суперпозицией функций
f u .
Степенная, показательная, логарифмическая, тригонометрические и обратные
тригонометрические функции называются элементарными.
Всякая функция, которая получается из основных элементарных путём конечного числа
суперпозиций и четырёх арифметических действий, называется элементарной
функцией.