Механические колебания

1. Лекция 5 Механические колебания

Образец подзаголовка
09.10.2019

2.

Лекция № 5
1. Модель гармонического осциллятора. Свободные
незатухающие колебания.
1.1. Основное уравнение движения
1.2. Основные характеристики.
1.3. Энергия гармонических колебаний.
2. Примеры незатухающих колебаний.
2.1. Пружинный маятник.
2.2. Математический маятник.
3. Свободные затухающие колебания
3.1. Дифференциальное уравнение
3.2. Основные характеристики колебаний
4. Вынужденные колебания
4.1. Дифференциальное уравнение
4.2. Амплитуда и фаза
4.3. Резонанс и резонансные кривые.
09.10.2019

3.

Колеба́ния — это повторяющийся во времени
процесс, в ходе которого система изменяет свое
состояние около точки равновесия.
Колебательные процессы широко распространены
в природе и технике (качели, натянутая струна,
переменный электрический ток и т.д.).
Физическая природа колебаний может быть
разной, поэтому различают колебания
механические, электрические, электромагнитные и
др. Однако различные колебательные процессы
описываются одинаковыми характеристиками и
одинаковыми уравнениями. Поэтому существует
единый подход к изучению колебаний различной
физической природы.
09.10.2019

4.

Колебания могут происходить только в том
случае, если при отклонении системы от
положения равновесия возникает сила (или
процесс), возвращающая систему в положение
равновесия. Такое равновесие называют
устойчивым. В точке устойчивого равновесия
возвращающая сила равна нулю.
FУПР ( x ) kx
FУПР (0) 0
09.10.2019

5.

Модель гармонического осциллятора.
Свободные незатухающие колебания.
Колебания называются свободными (или
собственными), если они совершаются за счет
первоначально сообщенной энергии при последующем
отсутствии внешних воздействий на колебательную
систему. Простейшим типом колебаний являются
гармонические колебания - колебания, при которых
колеблющаяся величина изменяется со временем по
закону косинуса (синуса).
Рассмотрим прямолинейные колебания материальной точки вдоль оси х около положения устойчивого
равновесия, принятого за начало координат.
09.10.2019

6.

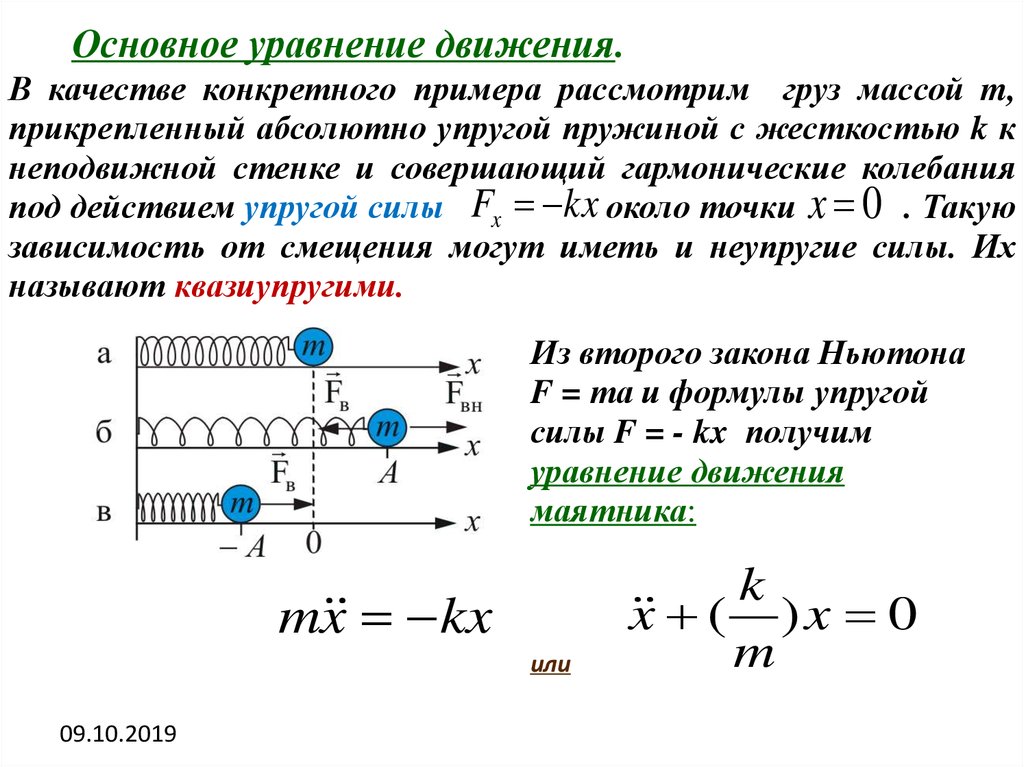
Основное уравнение движения.
В качестве конкретного примера рассмотрим груз массой m,
прикрепленный абсолютно упругой пружиной с жесткостью k к
неподвижной стенке и совершающий гармонические колебания
под действием упругой силы Fx kx около точки x 0 . Такую
зависимость от смещения могут иметь и неупругие силы. Их
называют квазиупругими.
Из второго закона Ньютона
F = mа и формулы упругой
силы F = - kx получим
уравнение движения
маятника:
m x kx
или
09.10.2019
k
x ( ) x 0
m

7.

x (
Обозначим
k
)x 0
m
k
m
Получим
основное
уравнение
динамики
гармонических колебаний, вызываемых упругими
силами:
ω02
Уравнение, содержащее производные, называют дифференциальным
уравнением. Решением дифференциального уравнения всегда является
некоторая функция, которая при подстановке ее в уравнение
обращает его в тождество.
Можно убедиться, что решением нашего уравнения
является функция вида x Acos (ω0t φ)
,
описывающая
колебания
гармонического
осцилятора
09.10.2019

8.

Основное характеристики гармонического
осциллятора.
x A cos( 0t )
A
- амплитудой колебания,
максимальное значение колеблющейся
величины, величина неотрицательная,
0 - круговая (циклическая) частота,
( 0t ) - фаза колебания в момент времени t
- Начальная
фаза колебания в момент
времени t 0
Так как косинус изменяется в пределах от +1 до -1, то
может принимать значения от
09.10.2019
A
до
A
x

9.

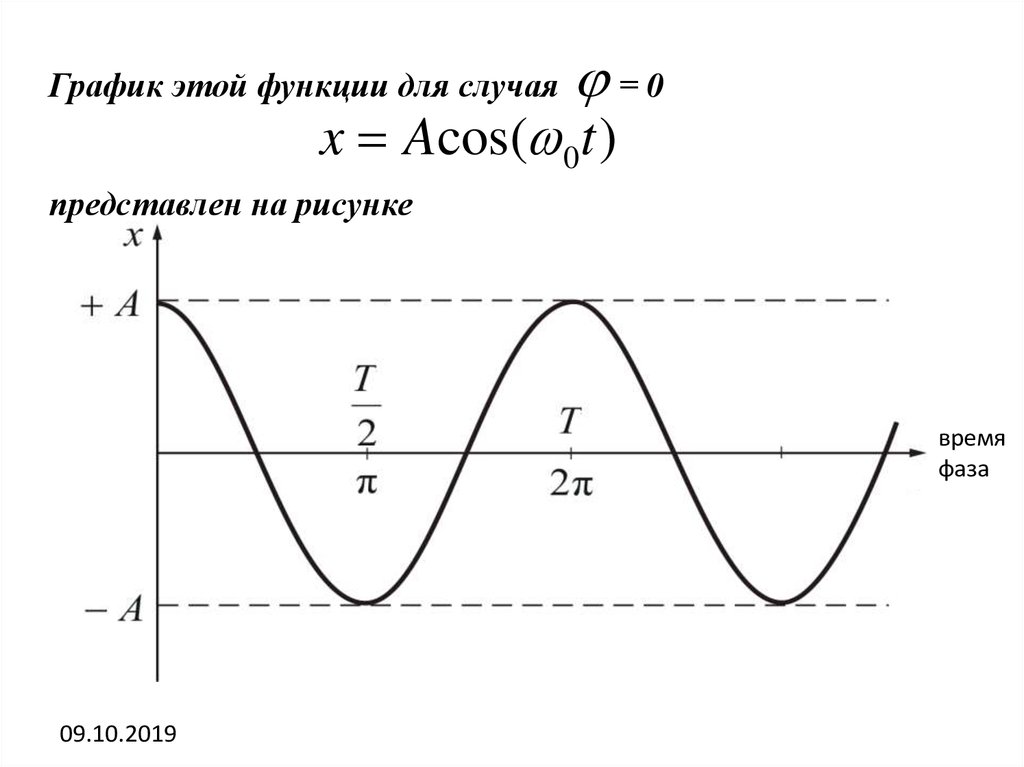
=0
x Acos( 0t )
График этой функции для случая
представлен на рисунке
время
фаза
09.10.2019

10.

Состояние системы, совершающей гармонические колебания,
повторяется через промежуток времени Т, называемый
периодом колебаний. За один период фаза колебания получает
приращение 2 , то есть
фаза колебания получает приращение
т.е
ω0(t + T) = ω0t + 2π
2
T
0
откуда
Величина, обратная периоду колебаний,
1
T
число колебаний, совершаемых в единицу
времени, называется частотой колебаний.
Нетрудно видеть, что 2
0
Единица частоты - герц (Гц).
09.10.2019

11.

Скорость и ускорение в колебательном процессе
x A cos( 0t )
Согласно определению, первая производная от
времени является скоростью:
x
по
Vx A 0 sin( 0t ) A 0 cos( 0t / 2)
Вторая производная от Х - ускорение:
ax A cos( 0t ) A cos( 0t )
2
0
2
0
Т.е. скорость и ускорение совершают гармонические
колебания с той же циклической частотой.
Амплитуды скорости и ускорения соответственно равны
0 A Vm и ω02 A am
Фаза колебаний скорости и ускорения отличается от
фазы колеблющейся величины x Acos (ω0t φ)
на / 2 и
соответственно.
09.10.2019

12.

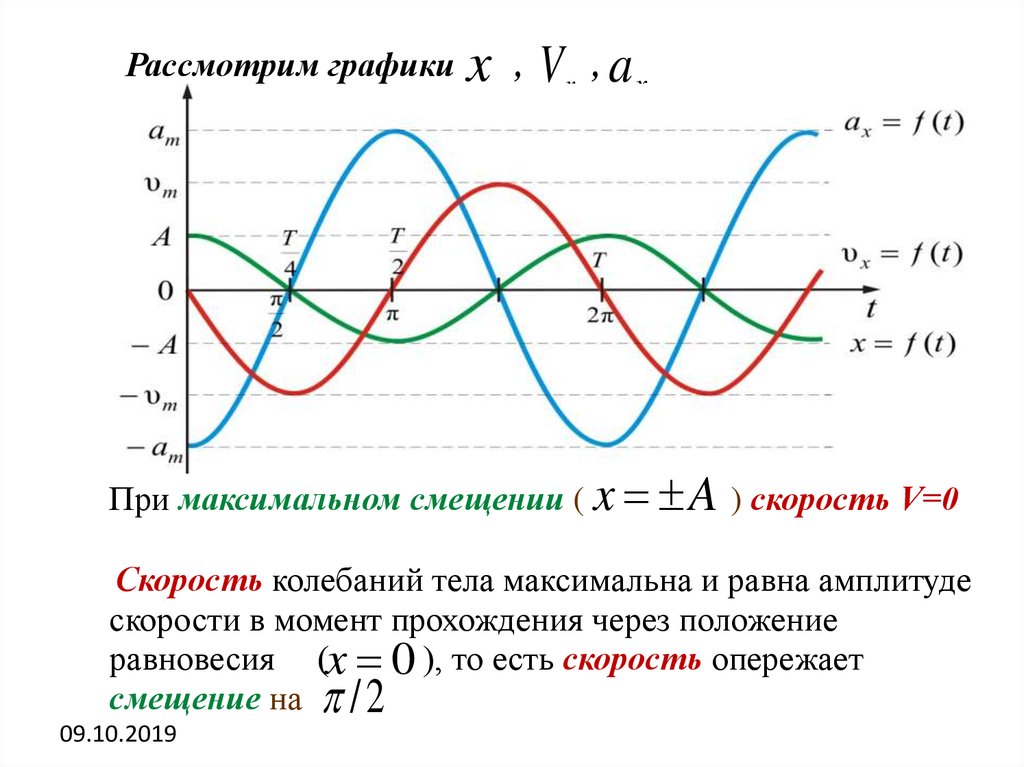
Рассмотрим графики
x , Vx , a x
При максимальном смещении ( x A ) скорость V=0
Скорость колебаний тела максимальна и равна амплитуде
скорости в момент прохождения через положение
равновесия (x 0 ), то есть скорость опережает
смещение на / 2
09.10.2019

13.

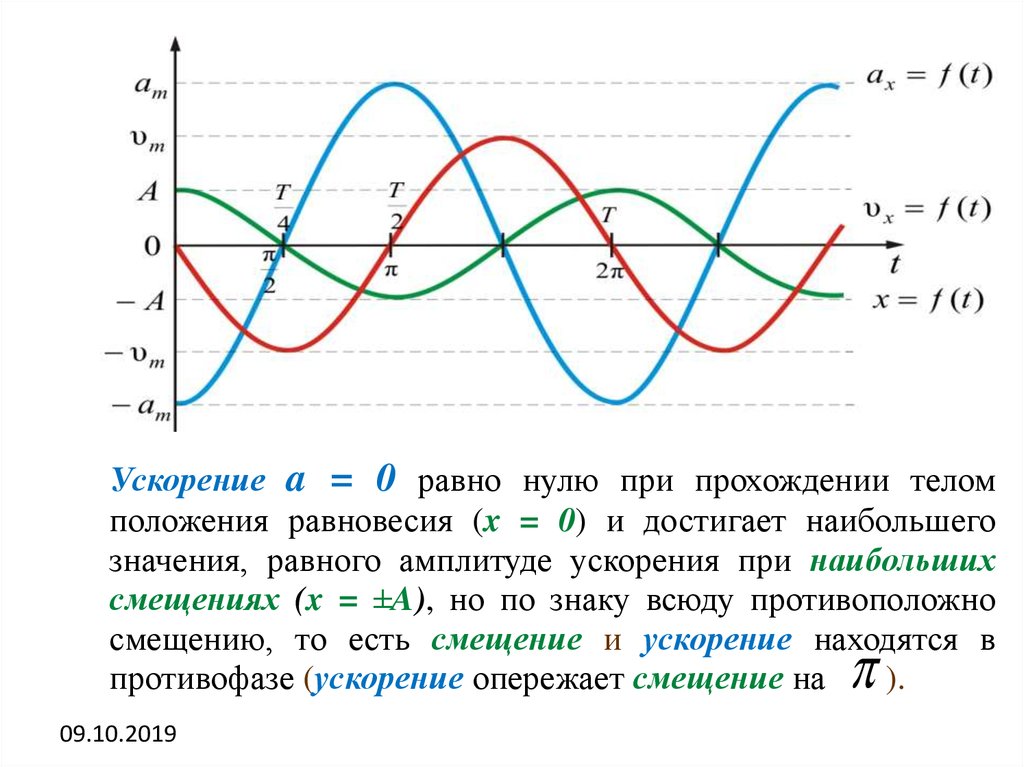
Ускорение a = 0 равно нулю при прохождении телом
положения равновесия (x = 0) и достигает наибольшего
значения, равного амплитуде ускорения при наибольших
смещениях (x = ±A), но по знаку всюду противоположно
смещению, то есть смещение и ускорение находятся в
противофазе (ускорение опережает смещение на
).
09.10.2019

14.

Энергия гармонических колебаний
складывается из кинетической энергии движения и
потенциальной энергии в поле упругой силы
Потенциальная энергия тела U измеряется той работой,
которую произведет возвращающая сила Fx kx . Так как
dU
Fx
dx
dU Fdx kxdx
x
kx2
U k xdx
2
0
, то
или
После подстановки выражения для х получаем для
потенциальной энергии следующую формулу:
2
kx 1 2
2
U
kA cos ( 0t )
2
2
09.10.2019

15.

или
1 2
U kA 1 cos 2( 0t )
4
Кинетическая энергия
mV2/2
m 2 2 2
kA2
K A 0 sin ( 0t )
sin 2 ( 0t )
2
2
или
2
kA
1 cos 2( 0t )
K
4
Из формул, приведенных в рамках следует, что U и K
изменяются с частотой 2 0 , которая в два
раза превышает частоту гармонического
колебания.
09.10.2019

16.

Сложив выражения для U и K, получим формулу для
полной энергии:
1 2 mA2 02
E K U kA
const
2
2
(учтено, что k = mω2)
Полная энергия остается постоянной, так как
при гармонических колебаниях справедлив закон
сохранения механической энергии, поскольку
упругая сила консервативна.
09.10.2019

17.

На рисунках представлены графики
зависимости х , U и K от времени.
Из графиков видно, что
происходит переход
кинетической энергии в
потенциальную и наоборот,
но их сумма в любой
момент времени
постоянна.
Из ранее полученных формул
для U и K, а также учитывая,
что средние значения
1
2
2
sin cos
2
следует:
K U
E
2
где Е — полная энергия
колебаний
09.10.2019

18.

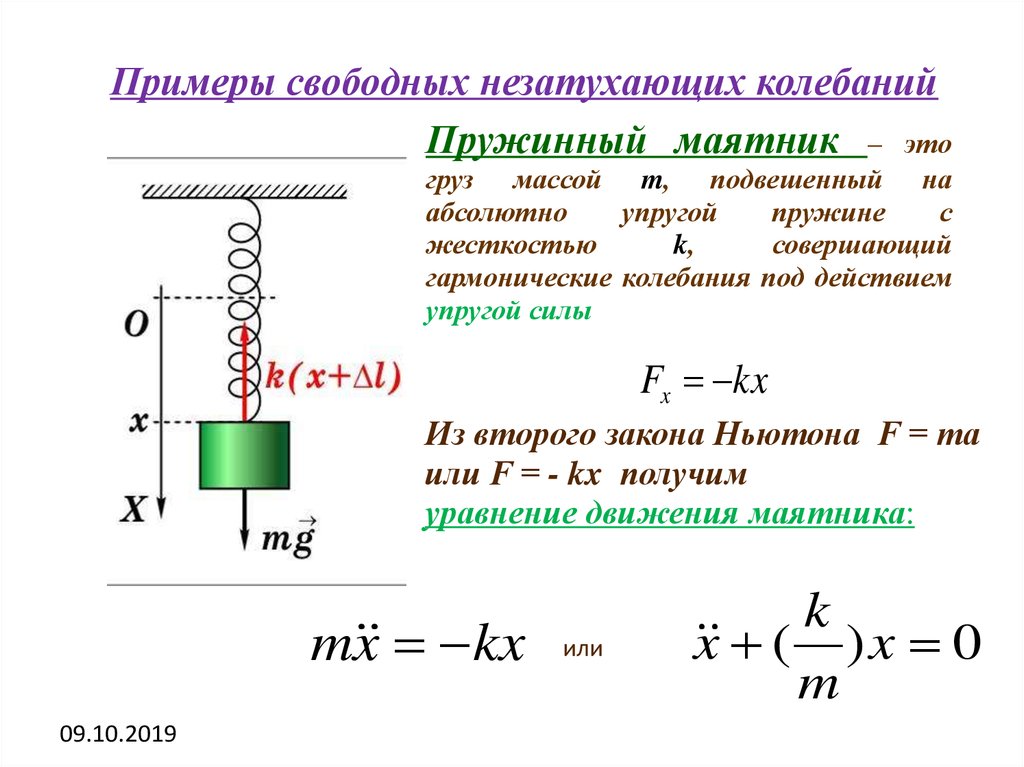
Примеры свободных незатухающих колебаний
Пружинный маятник – это
груз массой m, подвешенный на
абсолютно
упругой
пружине
с
жесткостью
k,
совершающий
гармонические колебания под действием
упругой силы
Fx kx
Из второго закона Ньютона F = mа
или F = - kx получим
уравнение движения маятника:
m x kx
09.10.2019
или
k
x ( ) x 0
m

19.

Решение этого уравнения – гармонические колебания вида:
x A cos( ω0t φ)
циклическая частота
период
09.10.2019
m
T 2
k
k
ω0
;
m

20.

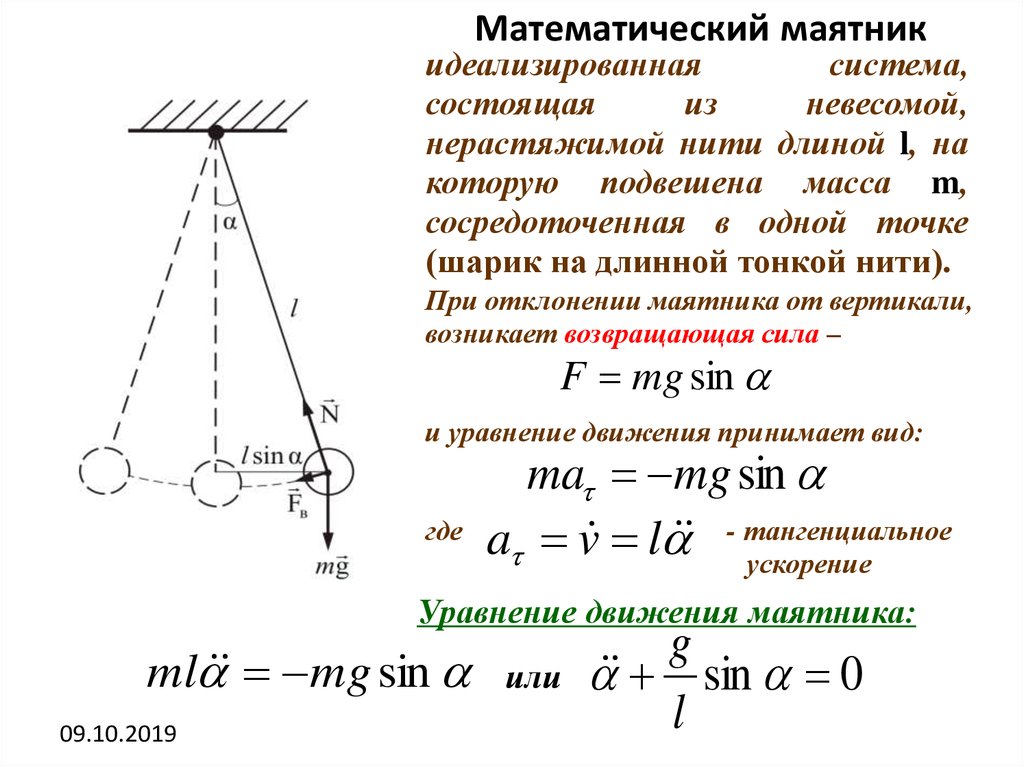
Математический маятник
идеализированная
система,
состоящая
из
невесомой,
нерастяжимой нити длиной l, на
которую подвешена масса m,
сосредоточенная в одной точке
(шарик на длинной тонкой нити).
При отклонении маятника от вертикали,
возникает возвращающая сила –
F mg sin
и уравнение движения принимает вид:
где
ma mg sin
a v l - тангенциальное
ускорение
Уравнение движения маятника:
ml mg sin
09.10.2019
или
g
sin 0
l

21.

Так как рассматриваются только малые отклонения
( sin ), уравнение движения маятника
можно упростить
g
0
l
Решением этого уравнения будут гармонические
колебания вида:
A cos( 0t )
с частотой
g
0 ;
l
периодом
l
T 2
g
период колебаний маятника зависит только от его
длины и не зависит от массы груза.
09.10.2019

22.

Образец подзаголовка
09.10.2019

23.

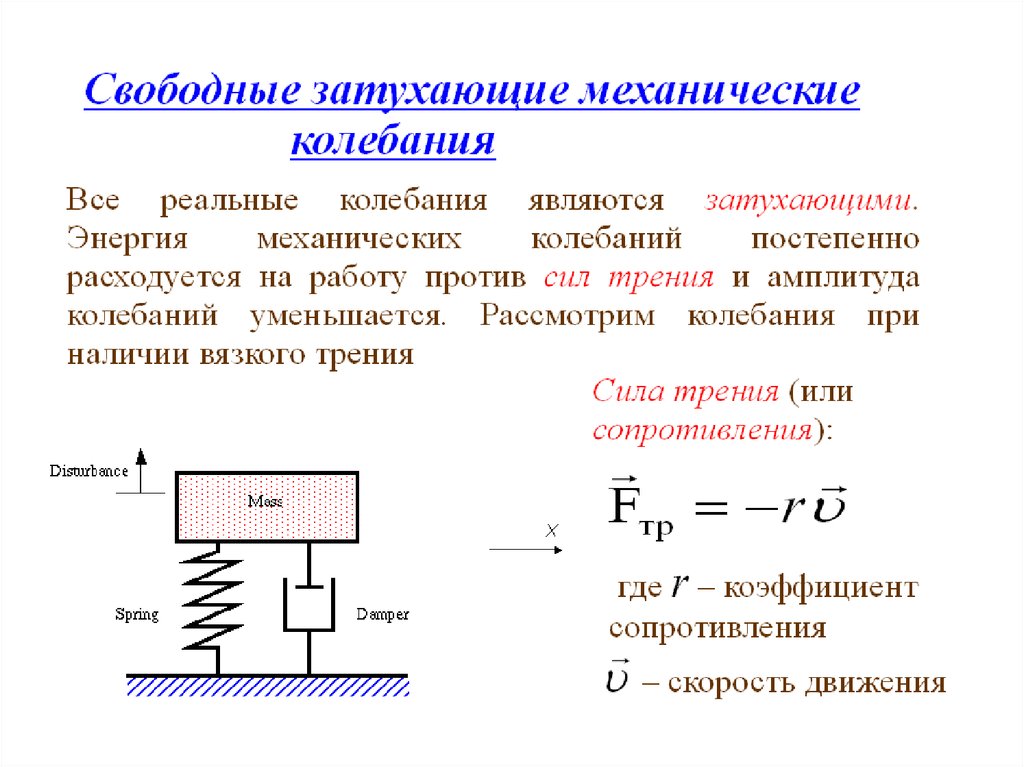
Второй закон Ньютона для затухающих колебаний вдоль
оси x примет вид :
max kx r x
где kx – возвращающая сила, r x – сила трения.
После несложных преобразований имеем:
r
k
x x x 0
m
m
Введем обозначения:
k
2
0
m
09.10.2019
квадрат
собственной
частоты
незатухающих
колебаний
r
2m
коэффициент
затухания

24.

Дифференциальное уравнение свободных
затухающих колебаний:
x 2 x x 0
2
0
2
Решение этого уравнения (при δ << 0 ) имеет вид:
x А0 e
t
Частота колебаний:
Период:
09.10.2019
cos( t )
2
0
2
2
2
T
,
2
2
0

25.

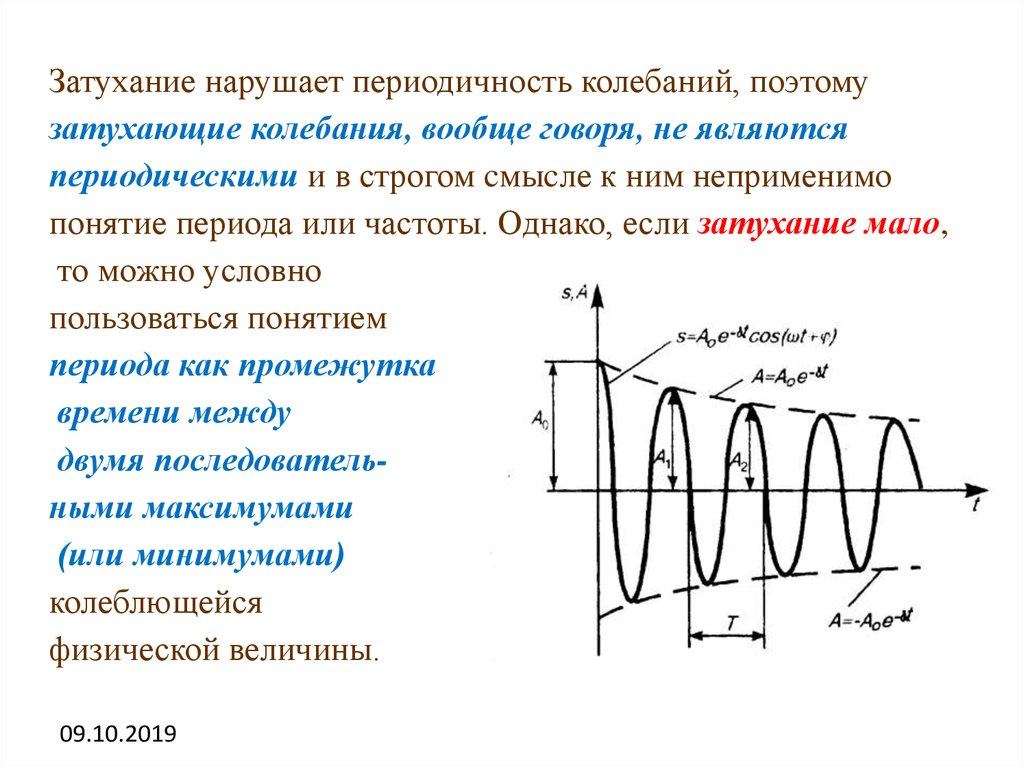
Затухание нарушает периодичность колебаний, поэтому
затухающие колебания, вообще говоря, не являются
периодическими и в строгом cмыcле к ним неприменимо
понятие периода или частоты. Однако, если затухание мало,
то можно условно
пользоваться понятием
периода как промежутка
времени между
двумя последовательными максимумами
(или минимумами)
колеблющейся
физической величины.
09.10.2019

26.

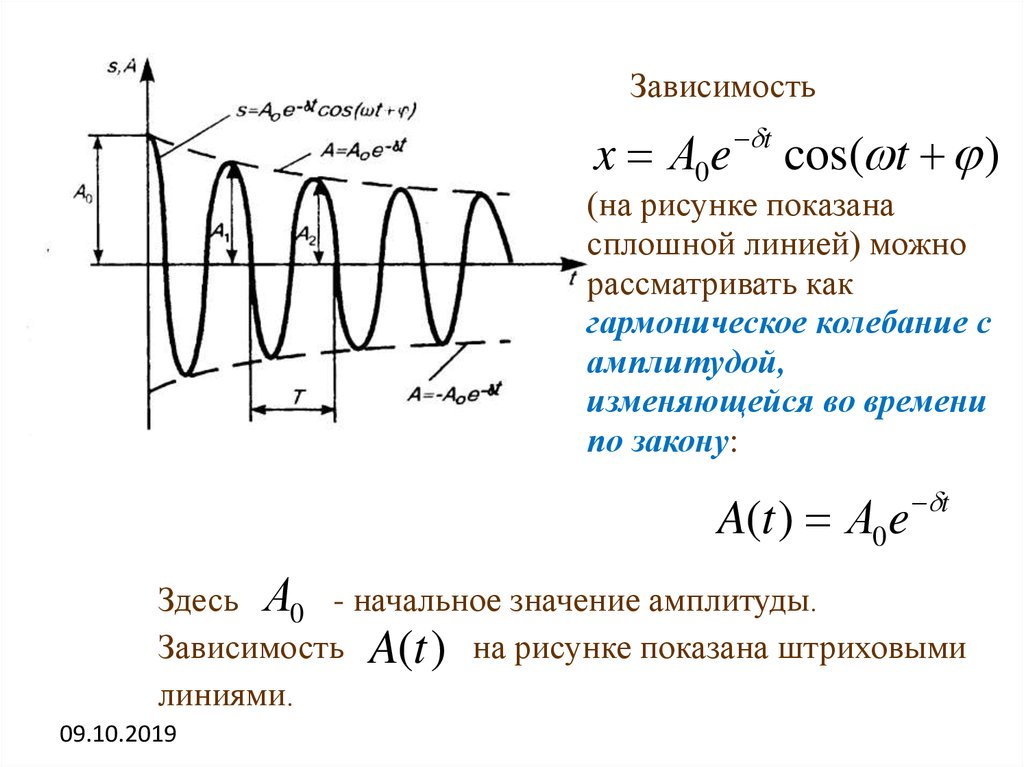
Зависимость
x А0 e t cos( t )
(на рисунке показана
сплошной линией) можно
рассматривать как
гармоническое колебание с
амплитудой,
изменяющейся во времени
по закону:
A(t ) А0 e
t
Здесь А0 - начальное значение амплитуды.
Зависимость A(t ) на рисунке показана штриховыми
линиями.
09.10.2019

27.

Основные параметры (характеристики)
затухающих колебаний
Время релаксации - τ - время, за которое амплитуда
уменьшается в е раз. Это условие выражается следующим
1
образом:
A( ) А0 e
A0 е
Из последнего равенства
1 / , то есть 1 /
Следовательно, коэффициент затухания
– есть
физическая величина, обратная времени, в течение
которого амплитуда уменьшается в е раз.
09.10.2019

28.

Число колебаний N e - число колебаний, по истечении
которых, амплитуда уменьшается
раз.
N eT
e
N e T 1 T
Логарифмическим декрементом затухания d
называется натуральный логарифм отношения
амплитуд, следующих друг за другом через период Т.
A(t )
d ln
ln e T T
A(t T )
d T
d 1 Ne
Логарифмический декремент характеризует, насколько
убывает амплитуда колебаний за период
09.10.2019

29.

Добротность Q является важнейшей
характеристикой колебательной системы, которая
при малых значениях коэффициента затухания
0
равна
Q Ne
d
T0 2
Добротность обратна логарифмическому декременту затухания
Физический смысл добротности выявляется из
рассмотрения энергии колебательной системы. Можно
показать, что добротность пропорциональна отношению
средней энергии <E>, запасенной осциллятором, к средним
потерям энергии <-ΔE> за период.
E
Q 2
E
09.10.2019

30.

r
2m
02 2
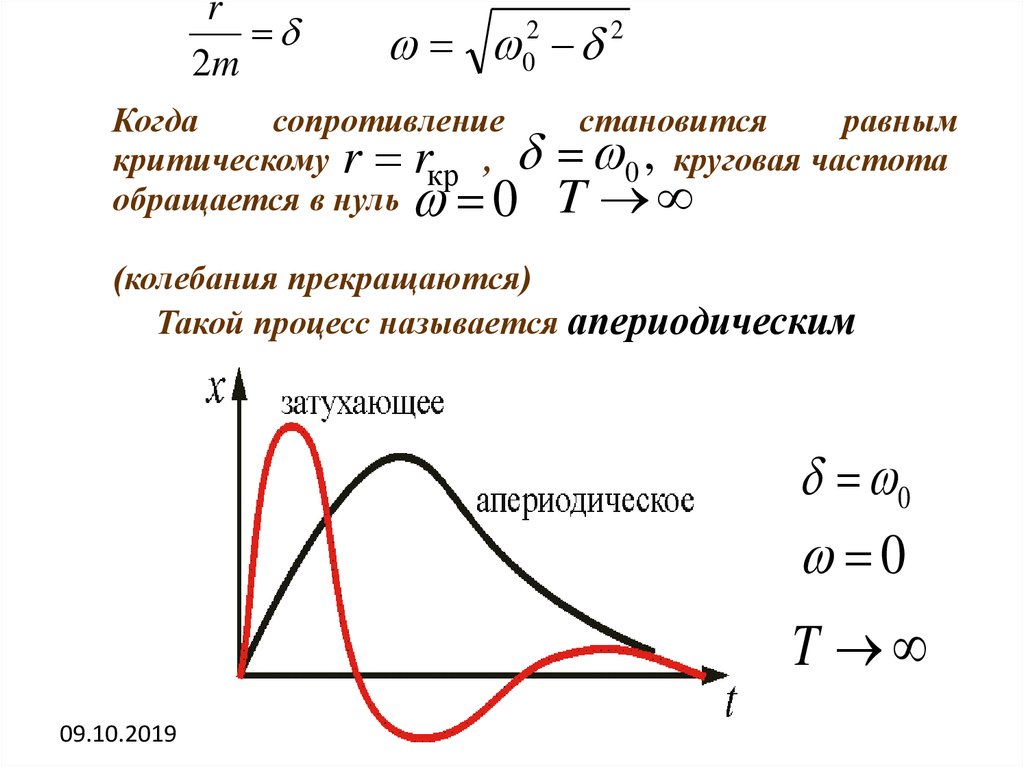
Когда
сопротивление
критическому r rкр ,
обращается в нуль
0
становится
равным
0 , круговая частота
T
(колебания прекращаются)
Такой процесс называется апериодическим
r rкр ,
0
0
T
09.10.2019

31.

Отличия
апериодического
процесса
от
рассмотренных
затухающих
колебаний
в
следующем.
При колебаниях, тело, возвращающееся в
положении
равновесия,
имеет
запас
кинетической энергии. В случае апериодического
движения энергия тела при возвращении в
положение
равновесия
оказывается
израсходованной
на
преодоление
сил
сопротивления трения.
09.10.2019

32.

Вынужденные колебания гармонического
осциллятора
Чтобы в реальной колебательной системе получить
незатухающие колебания, надо компенсировать потери
энергии. Такая компенсация возможна с помощью какоголибо периодически действующего фактора X(t)
,
изменяющегося по гармоническому закону:
X (t ) X 0 cos( t )
Если рассматривать механические колебания, то роль X(t)
играет внешняя вынуждающая сила
X (t )
F (t ) F0 cos( t )
Колебания под действием вынуждающей силы
называют вынужденными
09.10.2019

33.

Дифференциальное уравнение вынужденных
колебаний под действием гармонической силы
Рассмотрим систему, на которую кроме упругой силы (– kx)
и сил сопротивления (– rυ) действует добавочная
периодическая сила. Уравнение колебательного процесса
max kx r x Fx
где F F cos t.
x
0
С учетом обозначений для собственной частоты колебаний
системы и коэффициента затухания приходим к уравнению:
x 2 x 02 x ( F0 m) cos t
09.10.2019

34.

Решение этого уравнения в общем случае имеет сложный
вид, но для t >> 1/δ решение представляется в виде
x B cos( t )
где
- частота вынуждающей силы, а
соответственно формулами:
B
F0 m
( ) 4
09.10.2019
2
0
2 2
2
2
B и
задаются
2
arctg 2
0 2
Следовательно, в установившемся режиме вынужденные
колебания происходят с частотой
ω и являются гармоническими.
Амплитуда B и фаза φ колебаний существенно зависят от
частоты.

35.

B
F0 m
( 02 2 ) 2 4 2 2
Видно, что амплитуда колебаний имеет максимум при
некоторой частоте, которую называют резонансной
рез
Чтобы определить резонансную частоту, нужно найти
минимум подкоренного выражения в знаменателе.
Продифференцировав подкоренное выражение по
и
приравняв его нулю, получим условие, определяющее рез .
рез 2
2
0
2
Значение резонансной амплитуды:
B рез
09.10.2019
F0 m
2 02 2

36.

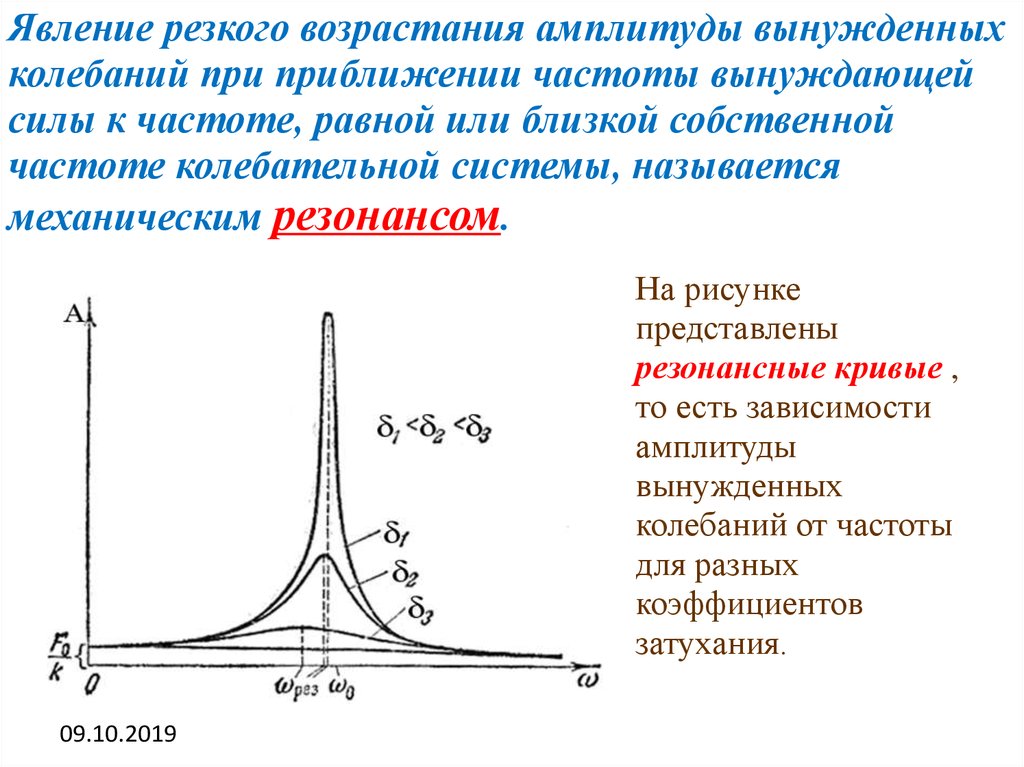
Явление резкого возрастания амплитуды вынужденных
колебаний при приближении частоты вынуждающей
силы к частоте, равной или близкой собственной
частоте колебательной системы, называется
механическим резонансом.
На рисунке
представлены
резонансные кривые ,
то есть зависимости
амплитуды
вынужденных
колебаний от частоты
для разных
коэффициентов
затухания.
09.10.2019

37.

При малом затухании:
Bрез
,
2
2
0
F0 m
2 0
Разделим полученную резонансную амплитуду на
статическое смещение системы из положения равновесия
под действием постоянной силы той же величины
Bст F0 m 02
Bрез
Bст
09.10.2019
F0
m 02 0
Q
m2 0 F0
2
Добротность показывает, во сколько раз
амплитуда в момент резонанса превышает
статическое смещение системы при
одинаковой силе.

38.

Зависимость сдвига фазы вынужденных колебаний
относительно частоты вынуждающей силы для
различных коэффициентов затухания :
2
arctg 2 2
0
1.
2.
0 0
рез
2
рез arctg
рез 0 2
2
2
0
3.
09.10.2019
0
рез 0
2