16f06f4435a74c0dbcba45be781fa1cd

1.

Подготовка к ОГЭ
Решение задач обязательной части
ОГЭ по геометрии
Задачи № 9, 10, 11, 12, 13
Модул
ь
«Геом
етрия»
содер
жит 8
задани
й: в
части
1-5
задани
йв
части 2 3
задани
я.

2.

Модуль «Геометрия» содержит 8 заданий:
в части 1 - 5 заданий, в части 2 - 3 задания.
Код по
КЭС
7.1
Название раздела содержания
Число заданий
Геометрические фигуры и их свойства.
Модуль
«Геометрия» содержит 8
7.2
Треугольник
7.3 вМногоугольники
заданий:
части 1 - 5 заданий, в час7.4
Окружность и круг
ти
2 - 3 задания.
7.5
Измерение геометрических величин
7.6
Векторы на плоскости
1
1
1
1
1
0

3.

Вашему вниманию представлены
тридцать пять
прототипов задач № 9, 10, 11, 12, 13
ОГЭ – 2015.
Задача № 9. 1, 2, 3, 4, 5, 6, 7
Задача № 10. 1, 2, 3, 4, 5, 6, 7
Задача № 11.
1, 2, 3, 4,85, 6, 7
Модуль «Геометрия»
содержит
заданий: в части
1 - 5№заданий,
Задача
12. 1, 2, 3,в4,час5, 6, 7
№ 13. 1, 2, 3, 4, 5, 6, 7
ти 2Задача
- 3 задания.

4.

Повторение (2)
Ответ: 70
4

5. Повторение

В равнобедренном треугольнике углы при
основании равны
В треугольнике сумма углов равна 180°
5

6.

Повторение (3)
∠ВСА = 180° - 57° - 117°=6°
Ответ: 6
6

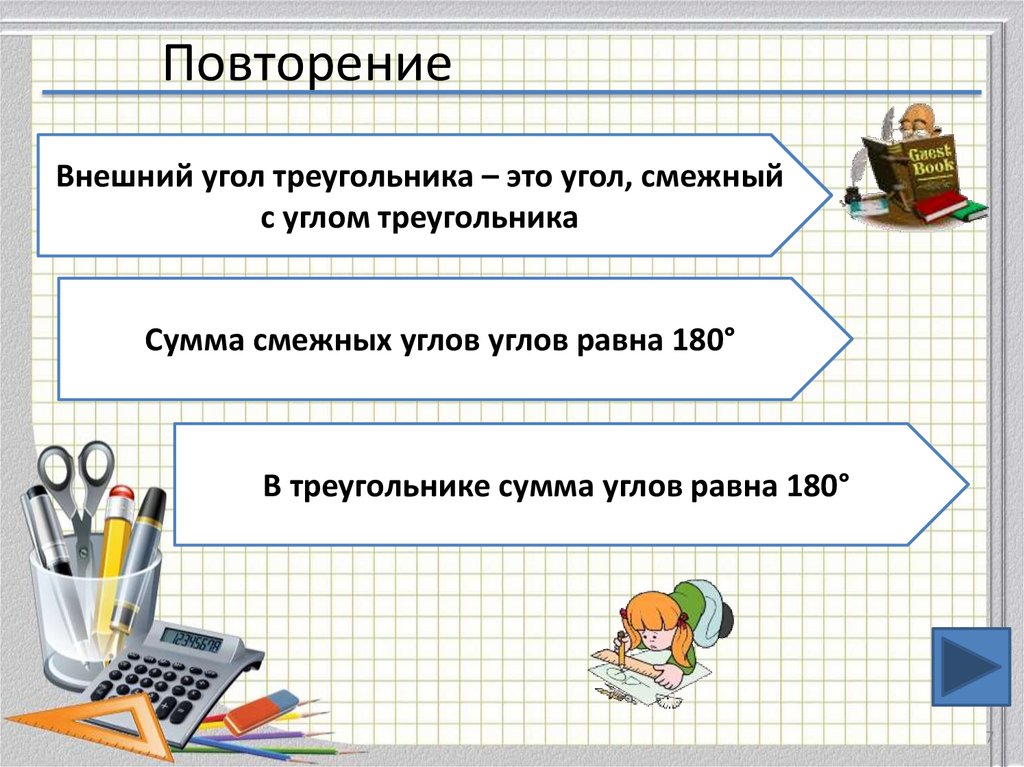
7. Повторение

Внешний угол треугольника – это угол, смежный
с углом треугольника
Сумма смежных углов углов равна 180°
В треугольнике сумма углов равна 180°
7

8.

Повторение (3)
BAC BAL LAC 23 23 46
Ответ: 111
8

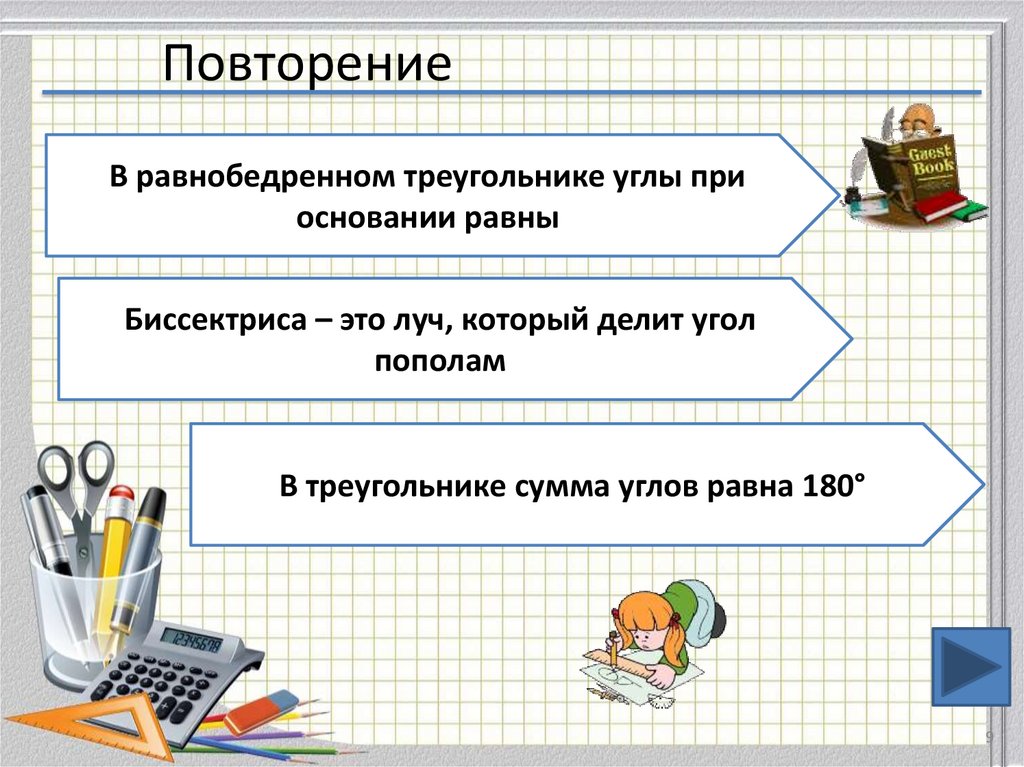
9. Повторение

В равнобедренном треугольнике углы при
основании равны
Биссектриса – это луч, который делит угол
пополам
В треугольнике сумма углов равна 180°
9

10.

Один из углов параллелограмма на
46° больше другого. Найти больший
из них.
∠А+∠D=180°
Повторение (2)
Пусть ∠А=х°, тогда∠D=(х+46)°
х+х+46=180
2х=134
х=67
∠D =2∙67°=134°
Ответ: 134
10

11. Повторение

Параллелограмм – это четырехугольник, у
которого противоположные стороны
параллельны.
Если две параллельные прямые пересечены
третьей, то сумма внутренних односторонних
углов равна 180°
11

12.

Найти больший угол
параллелограмма АВСD.
Повторение (2)
∠DCВ=∠АCD+∠АСВ=23°+49°=72°
∠С+∠В=180°
∠В=180°-∠В=180°-72°=108°
Ответ: 108
12

13. Повторение

Если угол разделен на части, то его градусная
мера равна сумме градусных мер его частей.
В параллелограмме сумма соседних углов
равна 180°
13

14.

Углы ромба относятся
как 3:7 .
Повторение
Найти больший
угол. (2)
∠1+∠2=180°
Пусть K – коэффициент пропорциональности,
тогда ∠2=(3k)°, ∠1=(7k)°
3k+7k=180
10k=180
k=18
∠1=18°∙7=126°
Ответ: 126
14

15. Повторение

В ромбе противоположные стороны
параллельны
Если две параллельные прямые пересечены
третьей, то сумма внутренних односторонних
углов равна 180°
15

16.

Разность
противолежащих
углов трапеции
Повторение (2)
равна 68°. Найти
больший угол.
∠А+∠В=180°
∠В=∠С
Если ∠А=х°, то ∠В = (х+68)°
х+х+68=180
2х=180-68
х = 56
∠В=56°+68°=124°
Ответ: 124
16

17. Повторение

В равнобедренном треугольнике углы при
основании равны.
Сумма углов, прилежащих боковой стороне
трапеции равна 180°.
17

18. Модуль «ГЕОМЕТРИЯ» №10 (1)

В
5
3
cos B
5
С
Найти АС.
А
ВС
cos B
АВ
⇒
ВС 3
АВ 5
Повторение (2)
⇒
ВС 3
По теореме Пифагора
2
2
2
2
АС АВ ВС 5 3 4
Ответ: 4
18

19. Повторение

Косинус острого угла прямоугольного
треугольника равен отношению прилежащего
катета к гипотенузе
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
19

20. Модуль «ГЕОМЕТРИЯ» №10 (2)

15
tgA
8
В
15
С
Найти АВ.
Повторение (2)
А
ВС
tgA
АC
⇒
ВС 15
АC 8
⇒
AС 8
По теореме Пифагора
2
2
2
2
АB АC ВС 8 15 17
Ответ: 17
20

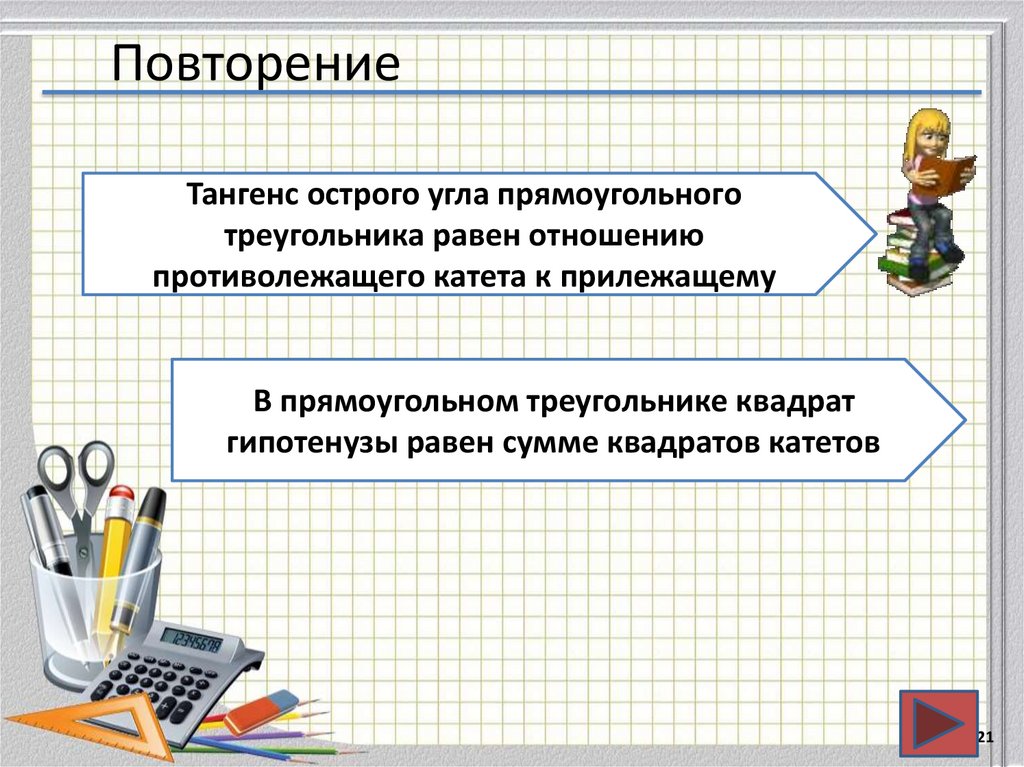
21. Повторение

Тангенс острого угла прямоугольного
треугольника равен отношению
противолежащего катета к прилежащему
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
21

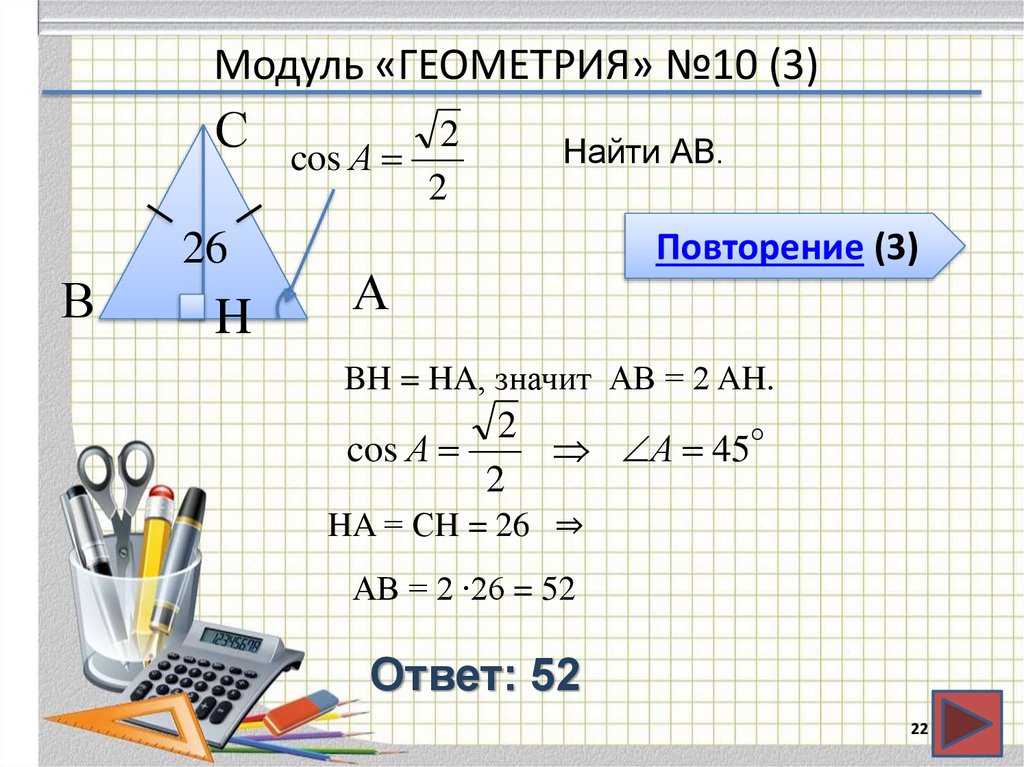
22. Модуль «ГЕОМЕТРИЯ» №10 (3)

С
В
26
H
2
cos А
2
Найти АВ.
А
Повторение (3)
BH = HA, значит АВ = 2 AH.
2
cos А
А 45
2
HA = СH = 26 ⇒
АВ = 2 ∙26 = 52
Ответ: 52
22

23. Повторение

Высота в равнобедренном треугольнике,
проведенная к основанию, является и медианой
В прямоугольном треугольнике сумма острых
углов равна 90⁰
Если в треугольнике два угла равны, то такой
треугольник равнобедренный
23

24. Модуль «ГЕОМЕТРИЯ» №10 (4)

С
Найти CH.
78 3
Повторение (2)
А
В
H
BH=HA, зн. АH=½ AB= 39 3
По теореме Пифагора в ∆ACH
СH АC 2 AH 2 (78 3)2 (39 3)2 117
Ответ: 117
24

25. Повторение

Высота в равнобедренном треугольнике,
проведенная к основанию, является и медианой
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
25

26. Модуль «ГЕОМЕТРИЯ» №10 (5)

С
Найти AB.
120⁰
Повторение (3)
25 3
В
H
А Проведем высоту CH, получим ∆ВCH.
∠ВCH=60⁰ ⇒ ∠CВH=30⁰
1
⇒ CH 25 3
2
По теореме Пифагора в ∆BCH
1
2
2
2
BH BC CH (25 3 ) ( 25 3 ) 2 37,5
2
AB 2 37,5 75
Ответ: 75
26

27. Повторение

Высота в прямоугольном треугольнике,
проведенная к основанию является
биссектрисой и медианой
В прямоугольном треугольнике катет, лежащий
против угла в 30⁰, равен половине гипотенузы
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
27

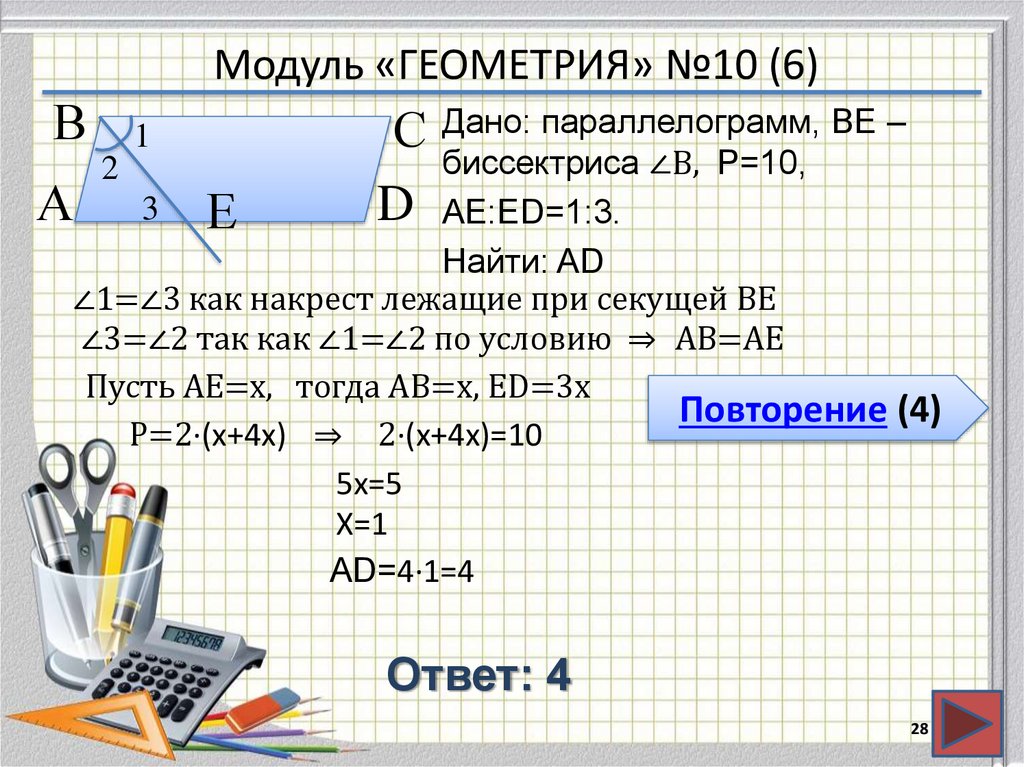
28. Модуль «ГЕОМЕТРИЯ» №10 (6)

В
А
1
2
3
Е
С Дано: параллелограмм, BE –
биссектриса ∠B, P=10,
D АЕ:ЕD=1:3.
Найти: AD
∠1=∠3 как накрест лежащие при секущей ВЕ
∠3=∠2 так как ∠1=∠2 по условию ⇒ АВ=АЕ
Пусть АЕ=х, тогда АВ=х, ЕD=3х
Повторение (4)
Р=2∙(х+4х) ⇒ 2∙(х+4х)=10
5х=5
Х=1
AD=4∙1=4
Ответ: 4
28

29. Повторение

Биссектриса – это луч, который делит угол
пополам
Периметр многоугольника – это сумма длин всех
сторон многоугольника
При пересечении двух параллельных прямых
накрест лежащие углы равны
Если два угла в треугольнике равны, то
треугольник - равнобедренный
29

30. Модуль «ГЕОМЕТРИЯ» №10 (7)

В
М
А 51
С
?
H
94
E
К
D
АВСD – трапеция, AH=51,
HD=94
Найти среднюю линию трапеции
Повторение (3)
Проведем СЕ⍊AD, получим ∆ABH=∆CED и
прямоугольник BCEH
⇒
AH=ЕD=51, BC=HE=HD-ED=94-51=43,
⇒ AD=AH+HE+ЕD= 51+94=145
AD BC
MK
⇒
2
145 43
MK
94
2
Ответ: 94
30

31. Повторение

Если гипотенуза и катет одного прямоугольного
треугольника соответственно равны гипотенузе и
катету другого треугольника, то треугольники равны
Если отрезок точкой разделен на части, то его
длина равна сумме длин его частей
Средняя линия трапеции равна полусумме
оснований трапеции
31

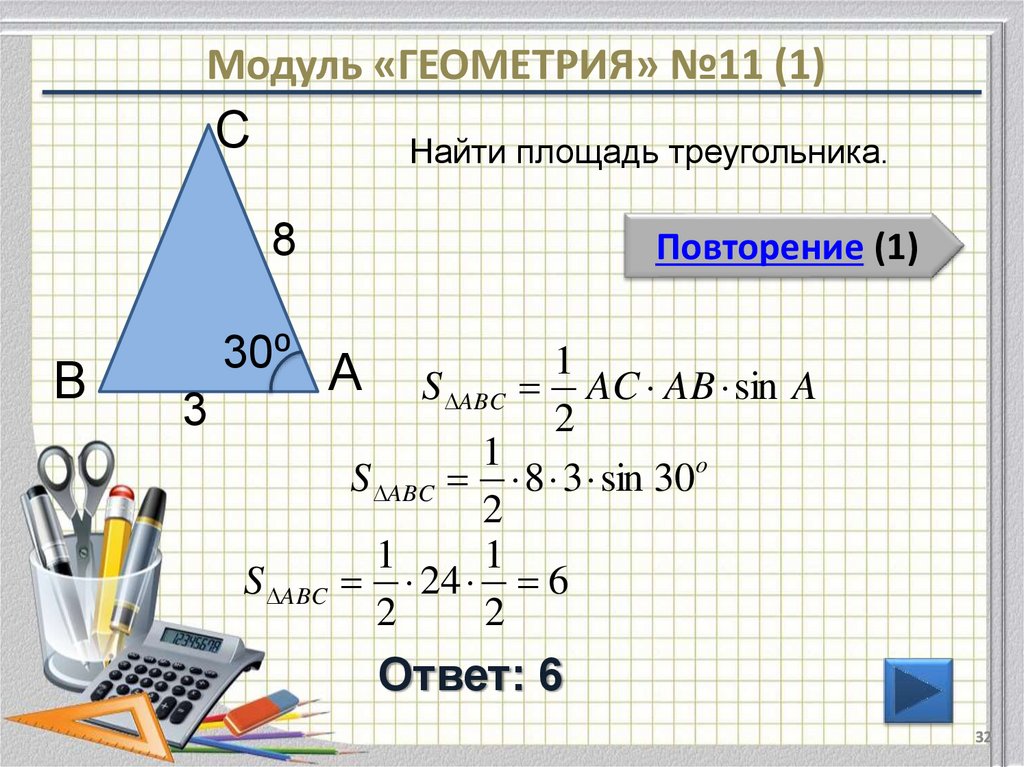
32. Модуль «ГЕОМЕТРИЯ» №11 (1)

С
Найти площадь треугольника.
8
В
30⁰
Повторение (1)
А
1
S ABC AC AB sin A
3
2
1
S ABC 8 3 sin 30o
2
1
1
S ABC 24 6
2
2
Ответ: 6
32

33. Повторение

Площадь треугольника равна половине
произведения двух сторон на синус угла между
ними
33

34. Модуль «ГЕОМЕТРИЯ» №11 (2)

С
В H
3
АВ=3CH.
Найти площадь треугольника
АВС
А
Повторение (2)
АВ=3CH=3∙3=9
1
S ABC AB CH
2
1
S ABC 3 9 13,5
2
Ответ: 13,5
34

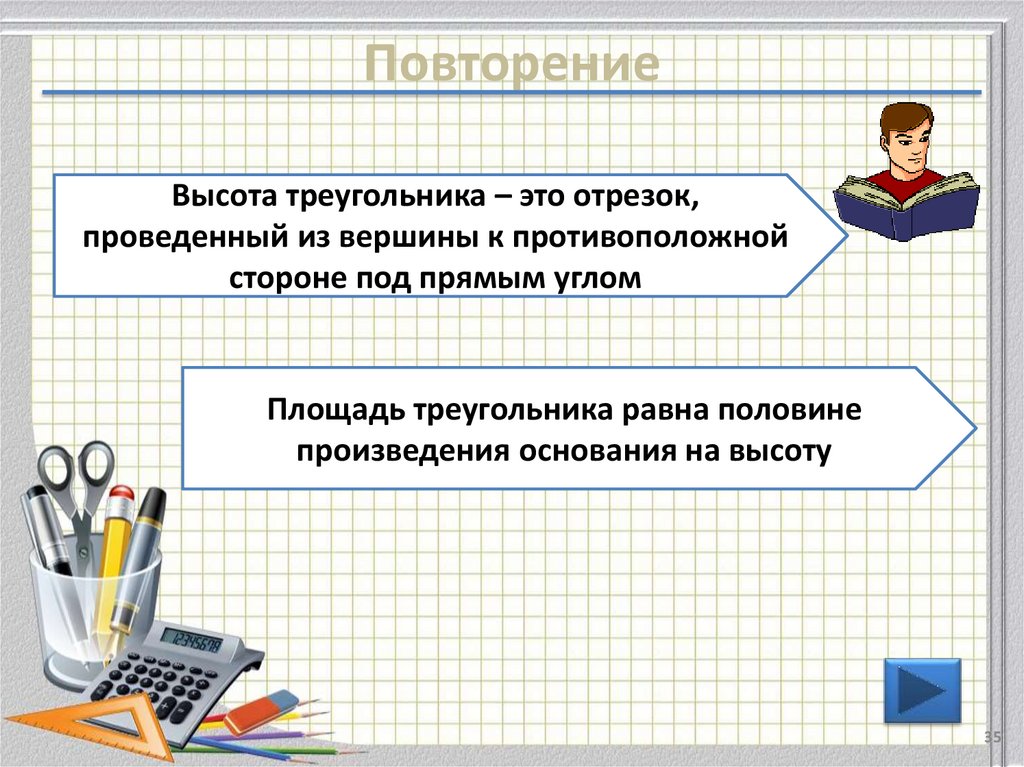
35. Повторение

Высота треугольника – это отрезок,
проведенный из вершины к противоположной
стороне под прямым углом
Площадь треугольника равна половине
произведения основания на высоту
35

36. Модуль «ГЕОМЕТРИЯ» №11 (3)

С
D
В
8
5
А
2 Найти S∆ABC
cos A
.
2
Повторение (2)
S ABCD AD AB sin A
2 2
2
sin A 1 cos A 1 (
)
2
2
2
2
S ABCD 8 5
20 2
2
Ответ: 20 2
36

37. Повторение

Площадь параллелограмма равна
произведению двух сторон на синус угла между
ними
Сумма квадратов синуса и косинуса одного и
того же угла равна единице
37

38. Модуль «ГЕОМЕТРИЯ» №11 (4)

А
В
С
D
Диагонали ромба равны 12 и
7.
Найти площадь ромба.
Повторение (2)
1
S ABC AC BD
2
1
S ABC 12 7 42
2
Ответ: 42
38

39. Повторение

Ромб – это параллелограмм с равными
сторонами
Площадь ромба равна половине произведения
его диагоналей
39

40. Модуль «ГЕОМЕТРИЯ» №11 (5)

В
А
О
60⁰
С
АС=10.
Найти площадь прямоугольника
D
Повторение (5)
АО=ВО=10:2=5
В ∆АОВ, где ∠ВАО= ∠АВО=(180⁰-60⁰):2=60⁰ ⇒
АВ=5
По теореме Пифагора в ∆АВD
ÀD ÂD2 AÂ2 102 52 5 3
S AB AD 5 5 3 25 3
Ответ: 25 3
40

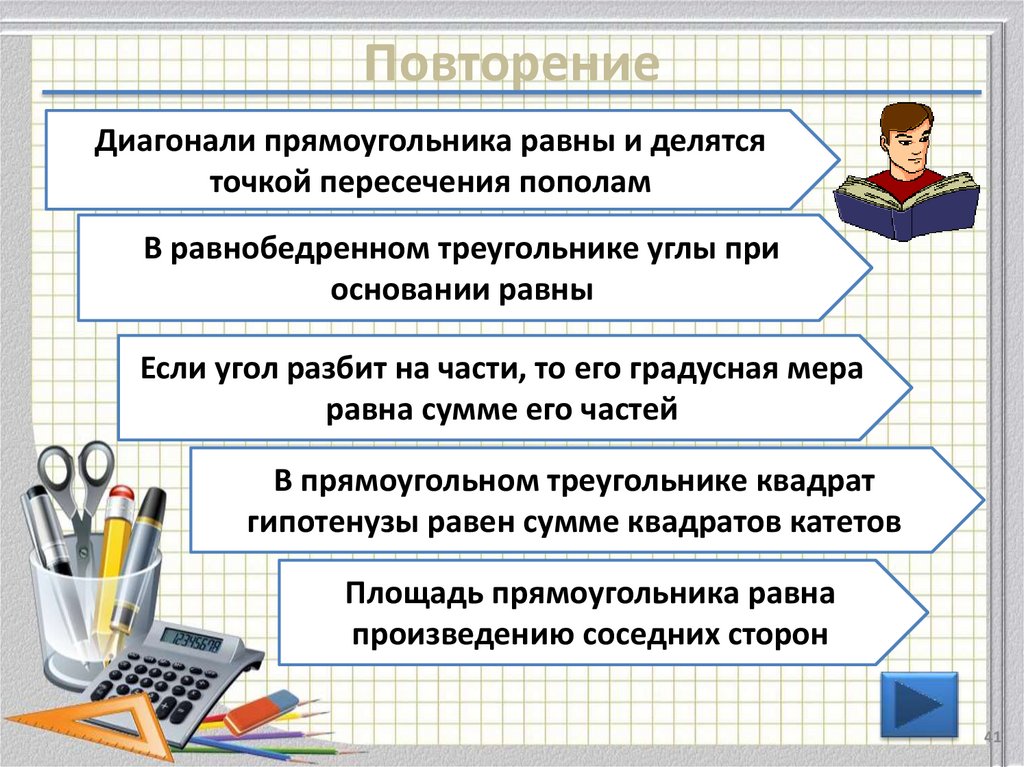
41. Повторение

Диагонали прямоугольника равны и делятся
точкой пересечения пополам
В равнобедренном треугольнике углы при
основании равны
Если угол разбит на части, то его градусная мера
равна сумме его частей
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
Площадь прямоугольника равна
произведению соседних сторон
41

42. Модуль «ГЕОМЕТРИЯ» №11 (6)

В
А H
С
14
ABCD – трапеция. ВС в 2 раза меньше
AD. Найти площадь трапеции
Повторение (2)
D
AD BC
S ABCD
BH
2
ВС=14:2=7
BC=BH=7
14 7
S ABCD
7 73,5
2
Ответ: 73,5
42

43. Повторение

Трапеция – это четырехугольник, две стороны
которого параллельны
Площадь трапеции равна произведению
полусуммы оснований на высоту
43

44. Модуль «ГЕОМЕТРИЯ» №11 (7)

В
А
М
135
⁰
8
С
К
H
AD BC
MK
8
2
∠АВH=135⁰-90⁰=45⁰
D
ABCD – равнобедренная
трапеция MK=8, боковая
сторона равна 5.
Найти площадь трапеции.
Повторение (4)
⇒
∠ВАH= ∠АВH=45⁰
По теореме Пифагора в ∆АВH, где AH=BH=х ⇒
1
1 2
5
BH
AÂ 2
5
2
2
2
AD BC
5
S ABCD
BH ⇒ S ABCD 8
20 2
2
2
Ответ: 20 2
44

45. Повторение

Площадь трапеции равна произведению
полусуммы оснований на высоту
Средняя линия трапеции равна полусумме
оснований
Если в прямоугольном треугольнике острый угол
равен 45⁰, то и другой острый угол равен 45⁰
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
45

46. Модуль «ГЕОМЕТРИЯ» №12 (1)

С
В
Найти угол АВС (в градусах)
Повторение (3)
А
Проведем из произвольной точки луча ВА перпендикуляр до
пересечения с лучом ВС
Получим прямоугольный равнобедренный треугольник
⇒
∠С=∠В=45⁰
по свойству острых углов прямоугольного
треугольника
Ответ: 45
46

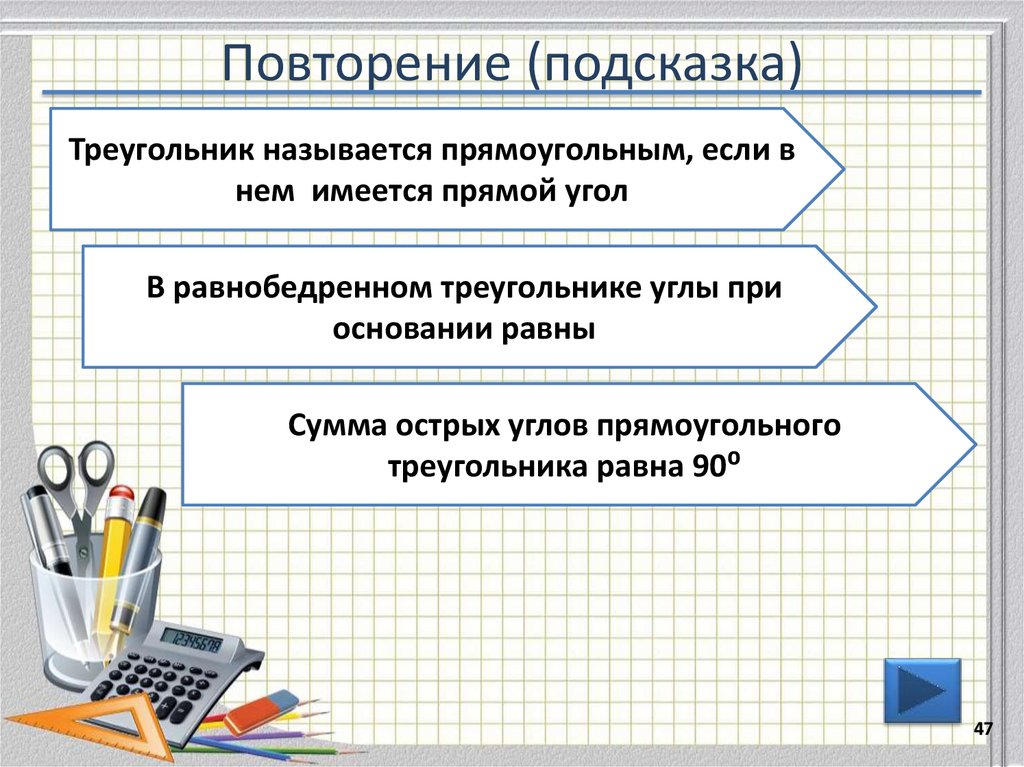
47. Повторение (подсказка)

Треугольник называется прямоугольным, если в
нем имеется прямой угол
В равнобедренном треугольнике углы при
основании равны
Сумма острых углов прямоугольного
треугольника равна 90⁰
47

48. Модуль «ГЕОМЕТРИЯ» №12 (2)

С
А
В
Найти угол АВС (в градусах)
D
Повторение (4)
Проведем из произвольной точки луча ВС перпендикуляр к
прямой АВ до пересечения с ней
Получим прямоугольный равнобедренный треугольник BCD
⇒ ∠С=∠В=45⁰ по свойству острых углов
прямоугольного треугольника
∠ABС+∠CВD=180⁰ как смежные ⇒
∠ABС=180⁰ - ∠CВD=135⁰
Ответ:135
48

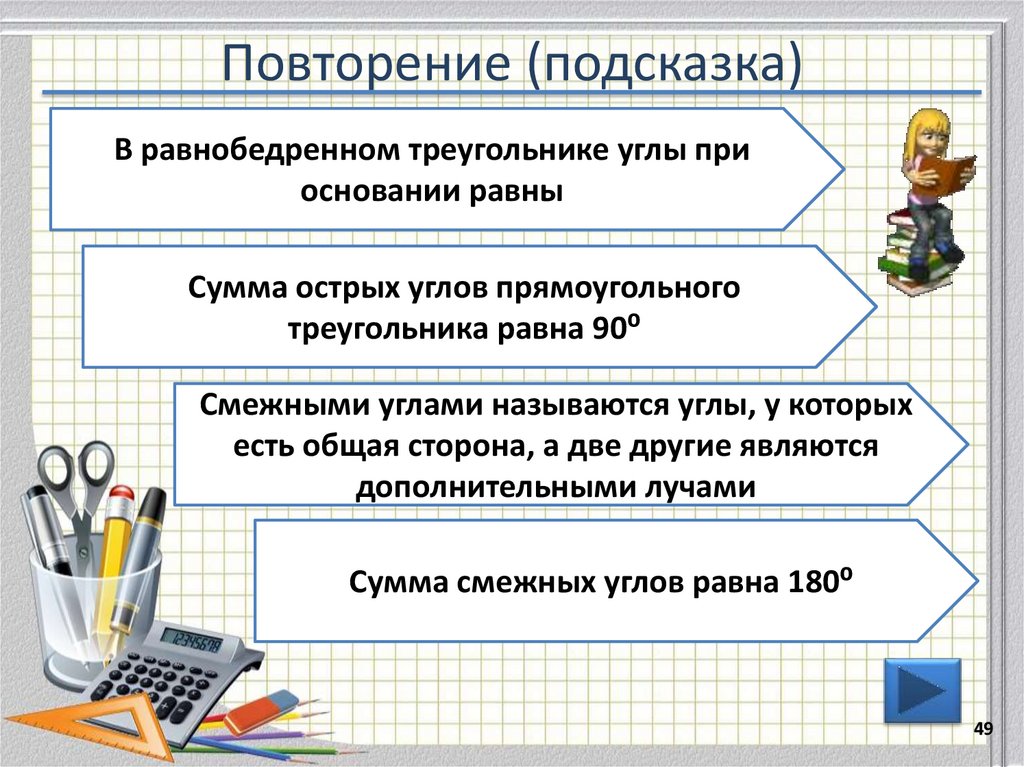
49. Повторение (подсказка)

В равнобедренном треугольнике углы при
основании равны
Сумма острых углов прямоугольного
треугольника равна 90⁰
Смежными углами называются углы, у которых
есть общая сторона, а две другие являются
дополнительными лучами
Сумма смежных углов равна 180⁰
49

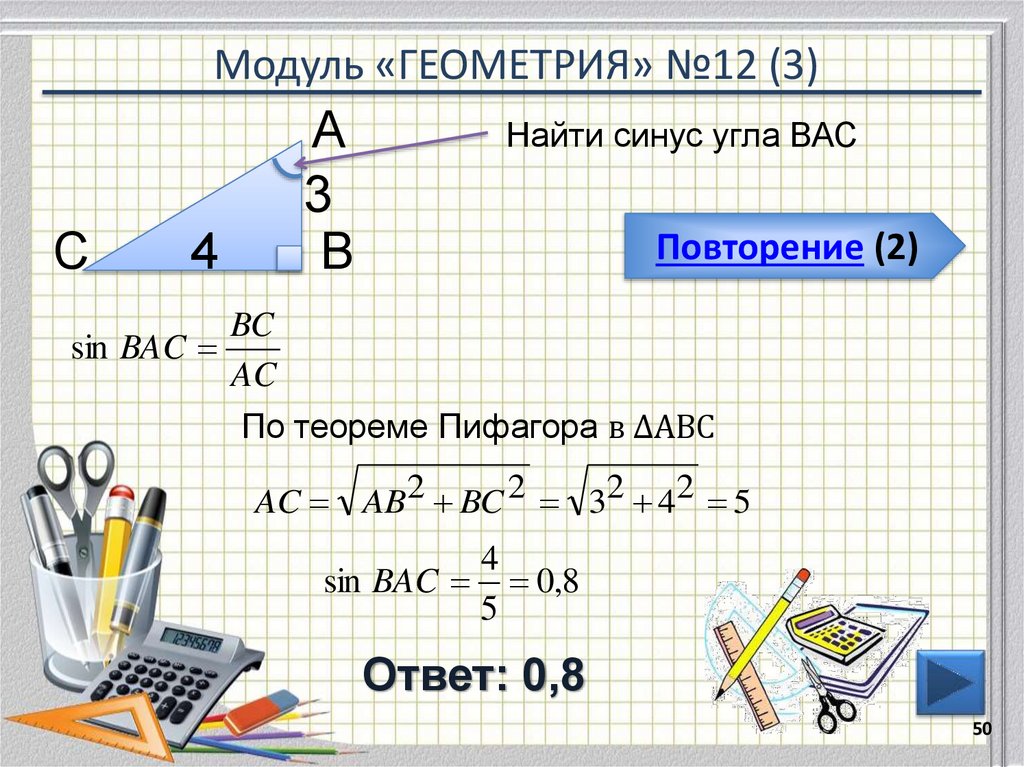
50. Модуль «ГЕОМЕТРИЯ» №12 (3)

С
4
А
3
В
Найти синус угла ВАС
Повторение (2)
BC
sin BAC
AC
По теореме Пифагора в ∆АВС
AC AB2 BC 2 32 42 5
sin BAC
4
0,8
5
Ответ: 0,8
50

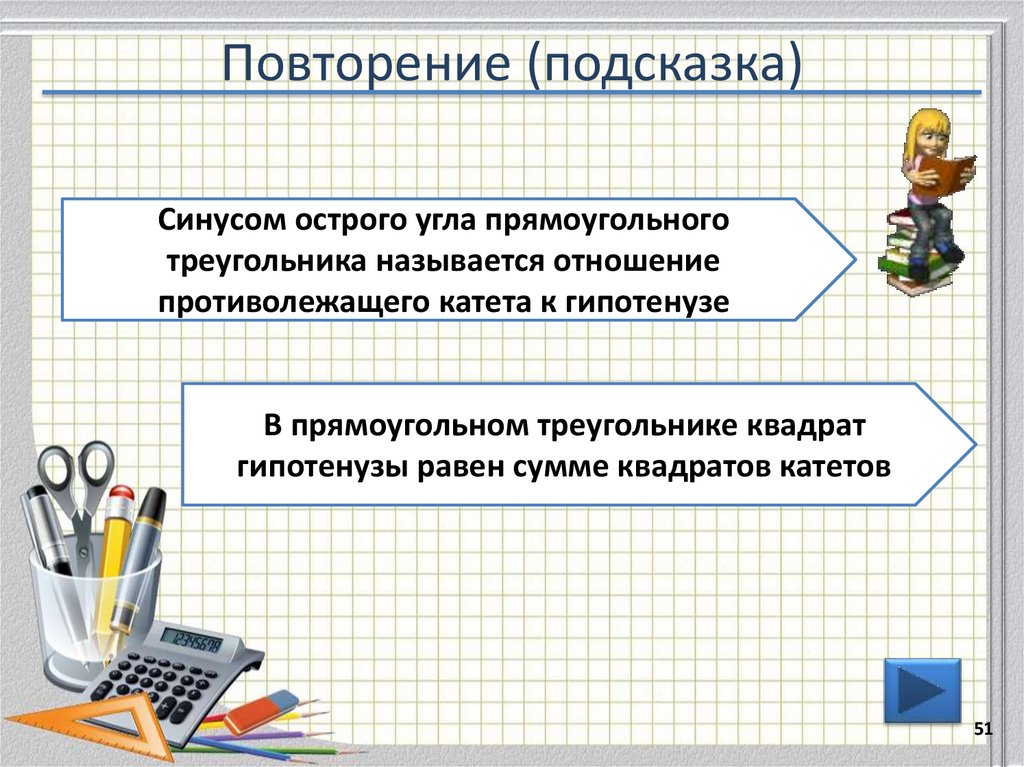
51. Повторение (подсказка)

Синусом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к гипотенузе
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
51

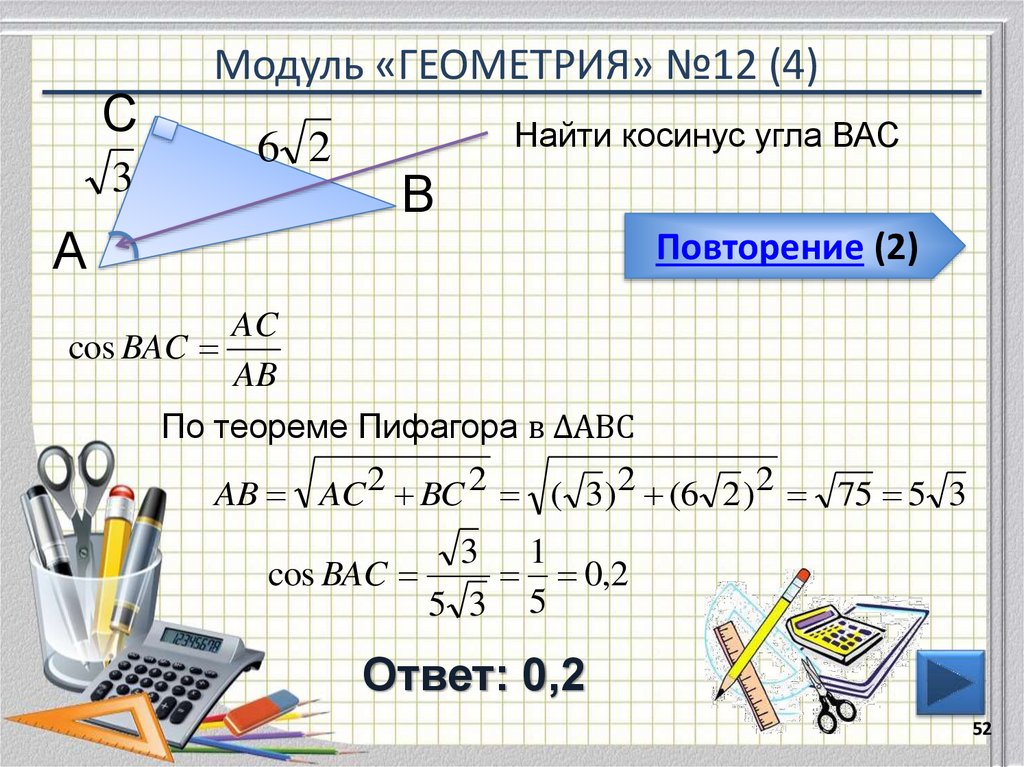
52. Модуль «ГЕОМЕТРИЯ» №12 (4)

С
3
А
Модуль «ГЕОМЕТРИЯ» №12 (4)
6 2
Найти косинус угла ВАС
В
Повторение (2)
AC
cos BAC
AB
По теореме Пифагора в ∆АВС
AB AC 2 BC 2 ( 3)2 (6 2 )2 75 5 3
3 1
cos BAC
0,2
5 3 5
Ответ: 0,2
52

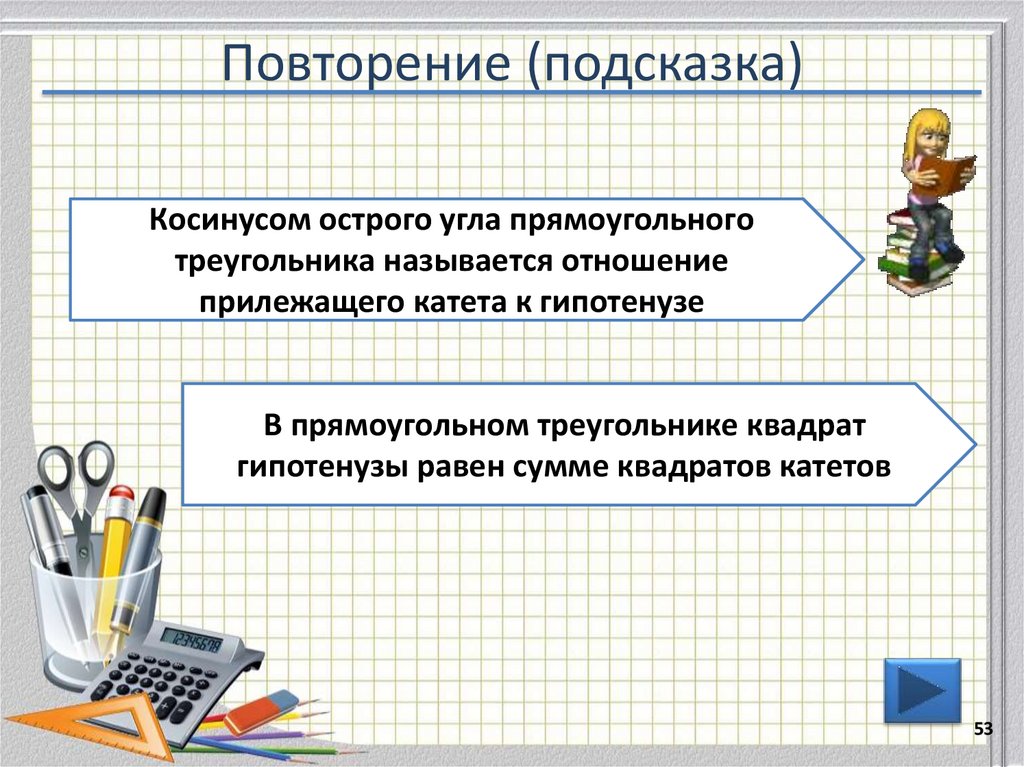
53. Повторение (подсказка)

Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
53

54. Модуль «ГЕОМЕТРИЯ» №12 (5)

А
Найти тангенс угла ВАС.
13
С
12
В
Повторение (2)
BC
tgBAC
AC
По теореме Пифагора в ∆АВС
AC AB 2 BC 2 132 122 5
12
tgBAC
2,4
5
Ответ: 2,4
54

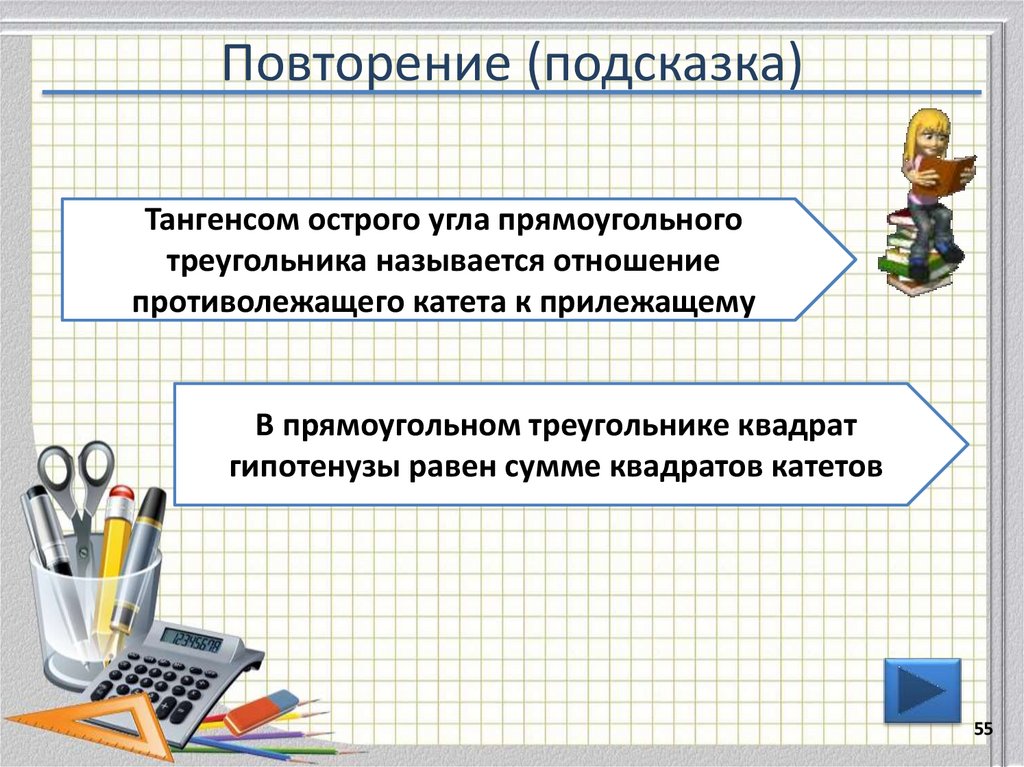
55. Повторение (подсказка)

Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
55

56. Модуль «ГЕОМЕТРИЯ» №12 (6)

Найти тангенс угла АВС.
С
В
А
Повторение (3)
Проведем из произвольной точки луча ВА перпендикуляр
до пересечения с лучом ВС.
Получим прямоугольный равнобедренный треугольник ⇒
∠С=∠В=45⁰ по свойству острых углов
прямоугольного тр-ка
0
tg 45 1
Ответ: 1
56

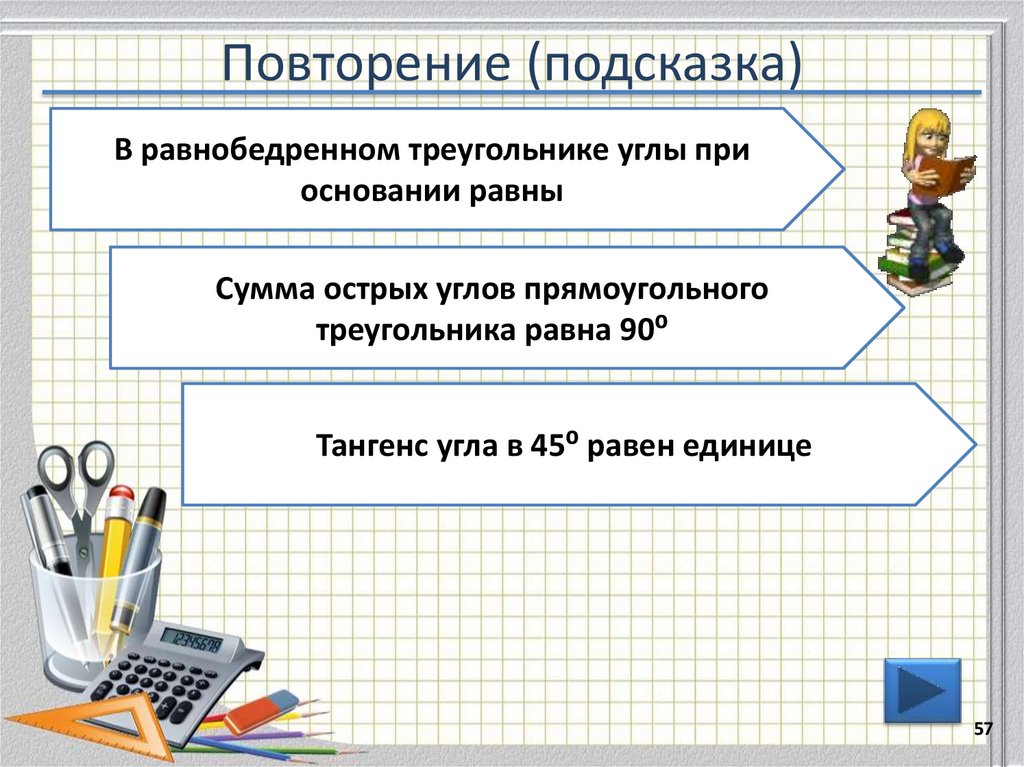
57. Повторение (подсказка)

В равнобедренном треугольнике углы при
основании равны
Сумма острых углов прямоугольного
треугольника равна 90⁰
Тангенс угла в 45⁰ равен единице
57

58. Модуль «ГЕОМЕТРИЯ» №12 (7)

Найти косинус угла АВС
С
В
А
Повторение (2)
Проведем перпендикуляр из такой точки луча ВА до
пересечения с лучом ВС, чтобы в катетах треугольника АВС
укладывалось целое число единиц измерения.
В данном случае единицей измерения стала клетка.
AB где АВ=3, АС=4, значит по
cos ABC
, теореме Пифагора ВС=5
BC
(Пифагоров треугольник)
3
cos ABC 0,6
5
Ответ: 0,6
58

59. Повторение (подсказка)

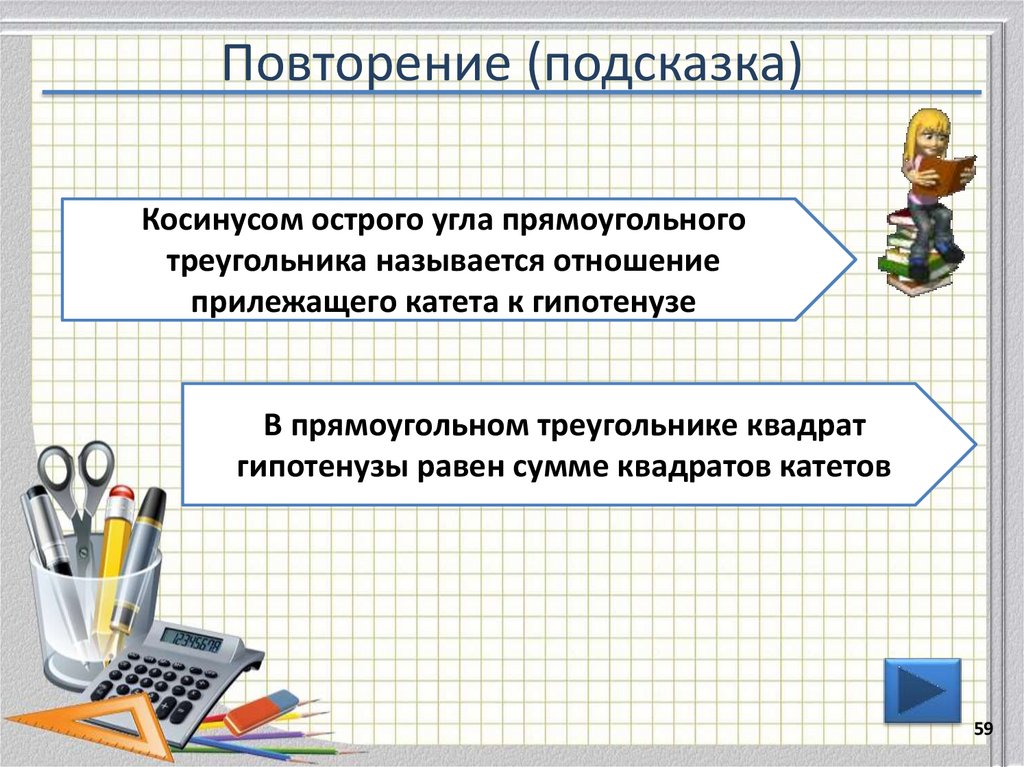
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
59

60. Модуль «ГЕОМЕТРИЯ» №13 (1)

Укажите номера верных утверждений
1.Через любые три различные точки
плоскости можно провести единственную
прямую.
да
нет
да
нет
2.Если угол равен 25⁰, то смежный с ним
угол равен 155⁰
да
нет
3.Через любую точку плоскости можно
провести не менее одной прямой
60

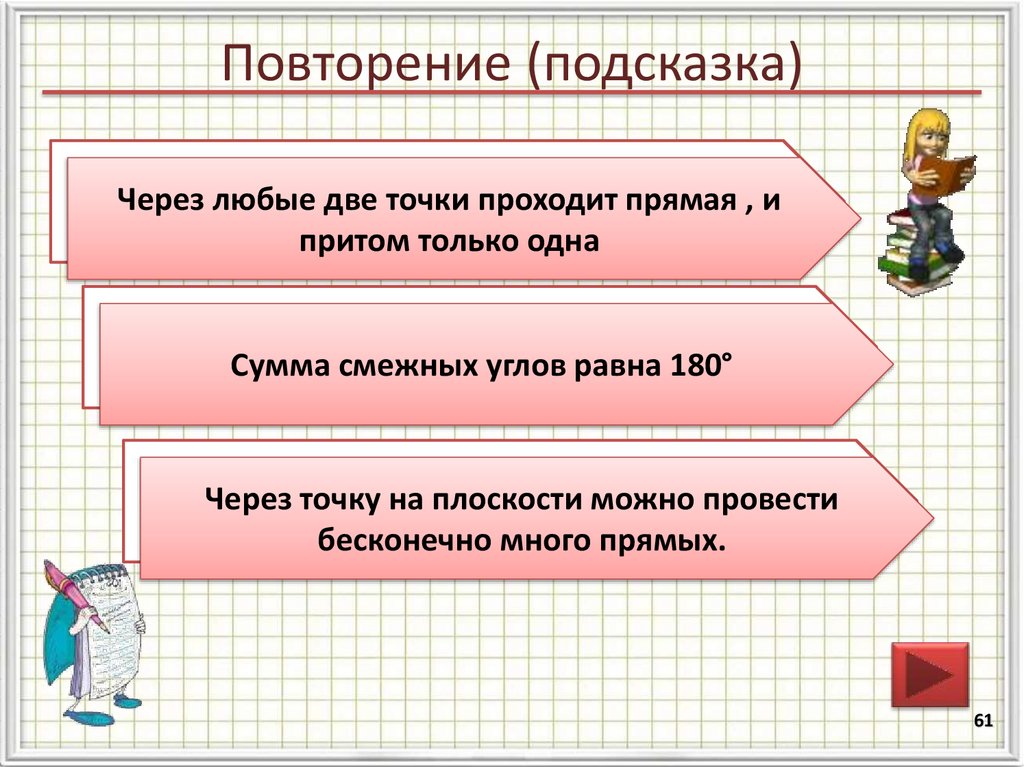
61. Повторение (подсказка)

Сформулируйте
аксиому
о взаимном
Через
любые две точки
проходит
прямая , и
расположении прямой и точек.
притом только одна
КакимСумма
свойством
обладают
углы?
смежных
угловсмежные
равна 180°
Сколько
прямых
можно
провести
через
точку на
Через
точку на
плоскости
можно
провести
плоскости?
бесконечно
много прямых.
61

62. Модуль «ГЕОМЕТРИЯ» №13 (2)

Укажите номера верных утверждений
да
нет
да
нет
да
нет
1.Если угол равен 56⁰, то вертикальный с
ним угол равен 124⁰.
2.Существует точка плоскости, через
которую можно провести бесконечное
количество различных прямых.
3.Через любую точку плоскости можно
провести не более двух прямых.
62

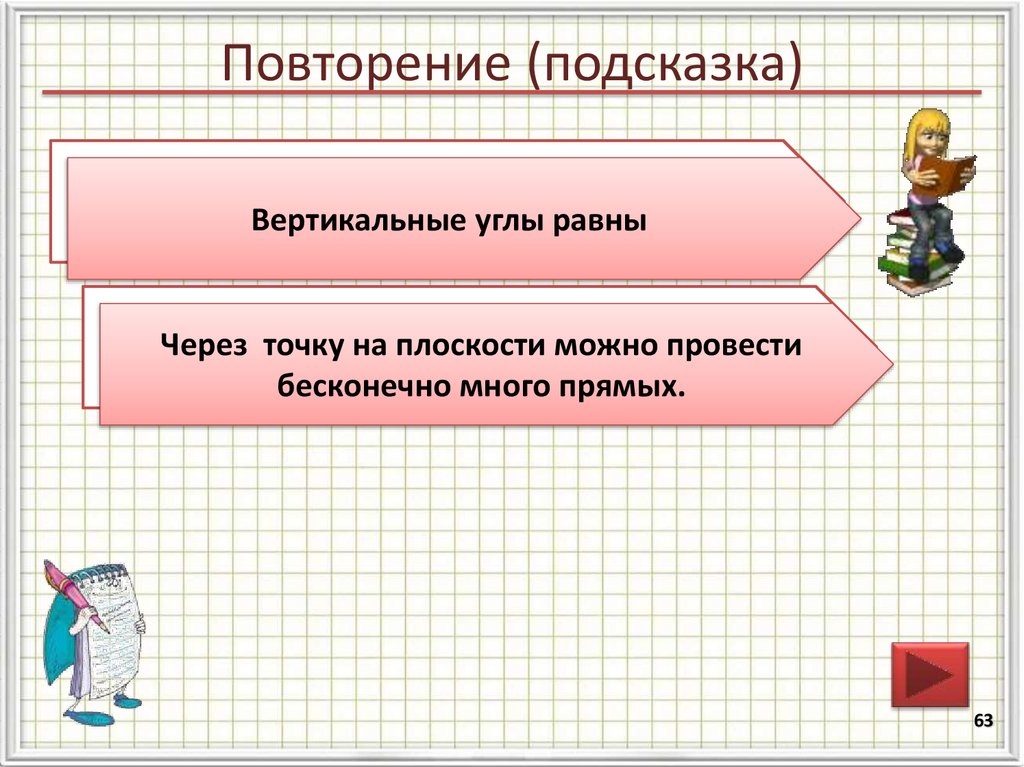
63. Повторение (подсказка)

Сформулируйте
свойство вертикальных
Вертикальные
углы равны углов.
Сколько
прямых
можно
провести
через
точку на
Через
точку на
плоскости
можно
провести
плоскости?
бесконечно
много прямых.
63

64. Модуль «ГЕОМЕТРИЯ» №13 (3)

Укажите номера верных утверждений
да
нет
да
нет
да
нет
1.Любые три различные прямые проходят
через одну общую точку.
2.Существует точка плоскости, не
лежащая на данной прямой, через
которую нельзя провести на плоскости ни
одной прямой, параллельной данной.
3.Если угол равен 47⁰, то смежный с ним
угол равен 133⁰.
64

65. Повторение (подсказка)

прямых
на плоскости
могут
иметь
однуна
Как Три
могут
взаимно
располагаться
три
прямых
общую точку, могут
пересекаться попарно, могут
плоскости?
и не иметь общих точек
Через точку, не лежащую на данной прямой,
Сформулируйте
аксиому
прямых.
проходит только
одна параллельных
прямая, параллельная
данной.
Сформулируйте
свойство
смежных
углов.
Сумма смежных
углов
равна 180°.
65

66. Модуль «ГЕОМЕТРИЯ» №13 (4)

Укажите номера верных утверждений
да
нет
да
нет
да
нет
1.Через любые две различные точки
плоскости можно провести не более
одной прямой.
2.Через любые две различные точки
плоскости можно провести не менее
одной прямой.
3.Если угол равен 54⁰, то вертикальный с
ним угол равен 36⁰.
66

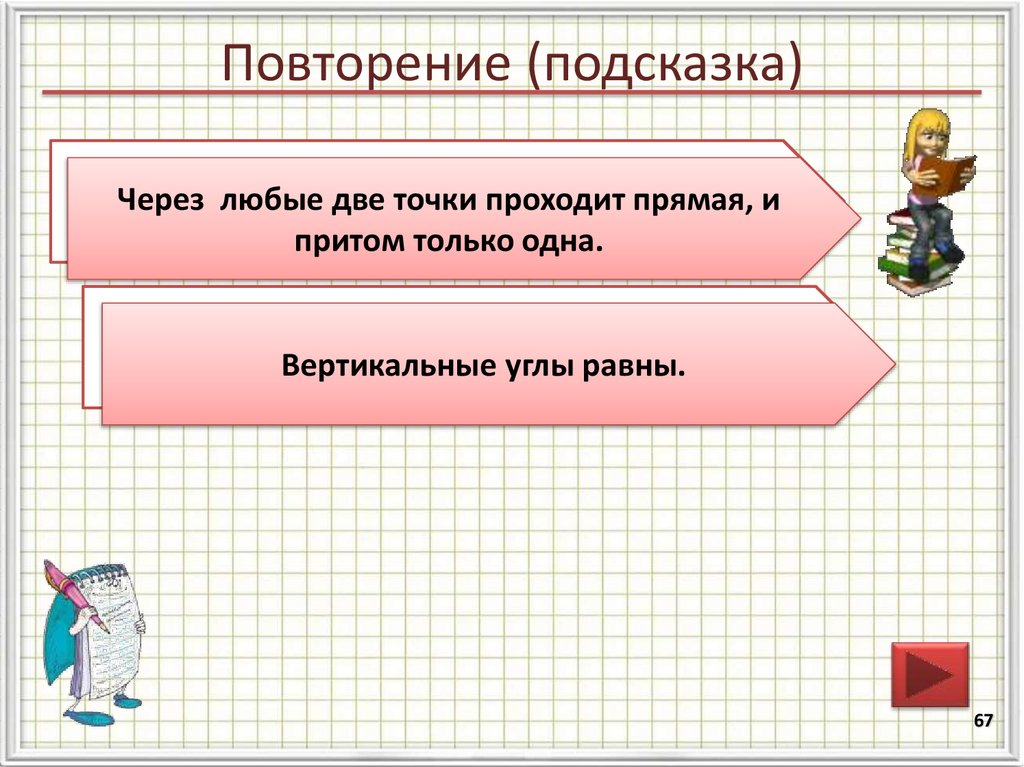
67. Повторение (подсказка)

Сформулируйте
аксиому
о взаимном
Через
любые две точки
проходит
прямая, и
расположении прямой и точек на плоскости.
притом только одна.
Сформулируйте
свойство углы
вертикальных
Вертикальные
равны. углов
67

68. Модуль «ГЕОМЕТРИЯ» №13 (5)

Укажите номера верных утверждений
да
нет
1.Через любую точку плоскости можно
провести прямую.
да
нет
2.Через любую точку плоскости можно
провести единственную прямую.
да
нет
3.Существует точка плоскости, через
которую можно провести прямую.
68

69. Повторение (подсказка)

Сколько прямых можно провести через точку на
Через точку на плоскости можно провести
плоскости?
бесконечно много прямых.
Существует
ли точку
точка плоскости
плоскости,можно
через которую
Через любую
провести
нельзя провести
прямую?
прямую.
69

70. Модуль «ГЕОМЕТРИЯ» №13 (6)

Укажите номера верных утверждений
да
нет
да
нет
да
нет
1.Если две параллельные прямые
пересечены третьей прямой, то
соответственные углы равны.
2.Если две параллельные прямые
пересечены третьей прямой, то сумма
внутренних односторонних углов равна 90⁰
3.Если при пересечении двух прямых
третьей соответственные углы равны, то
прямые перпендикулярны.
70

71. Повторение (подсказка)

Сформулируйте свойство параллельных прямых
Если две параллельные прямые пересечены
относительно соответственных углов
третьей прямой, то соответственные углы равны
Если две параллельные
прямые пересечены
Сформулируйте
свойство параллельных
прямых
третьейвнутренних
прямой, то односторонних
сума внутренних
относительно
углов.
односторонних углов равна 180°
71

72. Модуль «ГЕОМЕТРИЯ» №13 (7)

Укажите номера верных утверждений
да
нет
да
нет
да
нет
1.Если при пересечении двух прямых
третьей сумма внутренних накрест
лежащих углов равна 180⁰, то прямые
параллельны
2.Если при пересечении двух прямых
третьей соответственные углы равны 75⁰ и
105⁰, то прямые параллельны
3.Если при пересечении двух прямых
третьей сумма внутренних односторонних
углов равна 180⁰, то прямые параллельны
72

73. Повторение (подсказка)

Если при пересечении
прямых третьей
Сформулируйте
признак двух
параллельности
двух
накрест
лежащие углы
равны,
то прямые
прямых
относительно
накрест
лежащих
углов.
параллельны.
Если при пересечении
двух прямых третьей
Сформулируйте
признак параллельности
двух
соответственные
равны, то прямые
прямых
относительноуглы
соответственных
углов.
параллельны.
Сформулируйте
признак двух
параллельности
двух
Если при пересечении
прямых третьей
относительно
внутренних
суммапрямых
внутренних
односторонних
углов равна
односторонних
углов.
180°,
то прямые параллельны.
73

74. Рекомендации ученикам

4. Научитесь
выделять и понимать главное в
материале, т.к. умение решать задачи является
следствием
глубоко
понятого
соответствующего
теоретического материала.
5. Совершенствуйте свои вычислительные умения и
навыки.

75.

Книги по подготовке к ГИА
Модуль «Геометрия» содержит 8
заданий: в части 1 - 5 заданий, в части 2 - 3 задания.

76.

«ГИА-2015. Математика: типовые экзаменационные
варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В.
Ященко. – М.: Изд. «Национальное образование», 2014.
«ГИА-2015. Математика: учебно-тренировочные тесты по
новому плану ГИА под редакцией Ф. Ф. Лысенко,
С.Ю.Кулабухова. – Ростов –на-Дону: Легион, 2014.