Подготовка к ГИА. Решение задач обязательной части ГИА по геометрии. Задачи № 9, 10

1.

Подготовка к ГИА
Решение задач обязательной части
ГИА по геометрии
Задачи №
9, 108
Модуль «Геометрия»
содержит
заданий: в части 1 - 5 заданий, в части 2 - 3 задания.

2. Рассматриваемые вопросы:

1. Структура ГИА 2014.
2. Типичные ошибки.
3. Основные направления в работе.
4. Рекомендации учителям.
5. Рекомендации учащимся.
6. ЦОР по подготовке к ГИА.

3. ГИА по математике в 2013 году (235 минут)

1 часть
20 заданий
базового уровня
2 часть
4 задания
повышенного и 2
задания высокого
уровня

4. Работа состоит из трех модулей (необходимо набрать не менее 8 баллов)

Алгебра
(3 балла)
Геометрия
(2 балла)
Реальная
математика
( 2 балла)

5. Три формы заданий 1 части

Выбор одного
ответа из 4
предложенных
вариантов
(5 заданий)
С кратким
ответом
( 13 заданий)
Установления
соответствия между
объектами двух
множеств
(2 задания)

6. Типичные ошибки

Невнимательное
чтение условия и
вопроса задания
Неверное
применение
формул и свойств
фигур при решении
геометрических
задач
Вычислительные
ошибки
Раскрытие скобок
и применение
формул
сокращенного
умножения
Логические ошибки
при решении
текстовых задач .

7.

Вашему вниманию представлены
14
прототипов задач № 9, 10
Задача № 9. 1, 2, 3, 4, 5, 6, 7
Задача № 10. 1, 2, 3, 4, 5, 6, 7
Модуль «Геометрия» содержит 8
заданий: в части 1 - 5 заданий, в части 2 - 3 задания.

8.

Повторение (2)
Ответ: 70
8

9. Повторение

В равнобедренном треугольнике углы при
основании равны
В треугольнике сумма углов равна 180°
9

10.

Повторение (3)
∠ВСА = 180° - 57° - 117°=6°
Ответ: 6.
10

11. Повторение

Внешний угол треугольника – это угол, смежный
с углом треугольника
Сумма смежных углов углов равна 180°
В треугольнике сумма углов равна 180°
11

12.

Повторение (3)
Ответ: 111.
12

13. Повторение

В равнобедренном треугольнике углы при
основании равны
Биссектриса – это луч, который делит угол
пополам
В треугольнике сумма углов равна 180°
13

14.

Один из углов параллелограмма на
46° больше другого. Найти больший
из них.
∠А+∠D=180°
Повторение (2)
Пусть ∠А=х°, тогда∠D=х°+46°
х+х+46=180
2х=134
х=67
∠D =2∙67°=134°
Ответ: 134.
14

15. Повторение

Параллелограмм – это четырехугольник, у
которого противоположные стороны
параллельны.
Если две параллельные прямые пересечены
третьей, то сумма внутренних односторонних
углов равна 180°
15

16.

Найти больший угол
параллелограмма АВСD.
Повторение (2)
∠DCВ=∠АCD+∠АСВ=23°+49°=72°
∠С+∠В=180°
∠В=180°-∠В=180°-72°=108°
Ответ: 108.
16

17. Повторение

Если угол разделен на части, то его градусная
мера равна сумме градусных мер его частей.
В параллелограмме сумма соседних углов
равна 180°
17

18.

Углы ромба относятся
как 3:7 .
Повторение
Найти больший
угол. (2)
∠1+∠2=180°
Пусть х° - одна часть, тогда∠2=3х°, ∠1=7х°
3х+7х=180
10х=180
х=18
∠1=18°∙7=126°
Ответ: 126.
18

19. Повторение

В ромбе противоположные стороны
параллельны
Если две параллельные прямые пересечены
третьей, то сумма внутренних односторонних
углов равна 180°
19

20.

Разность
противолежащих
углов трапеции
Повторение (2)
равна 68°. Найти
больший угол.
∠А+∠В=180°
∠В=∠С
Если ∠А=х°, то ∠В=х°+68°
х+х+68=180
2х=180-68
х = 56
∠В=56°+68°=124°
Ответ: 124.
20

21. Повторение

В равнобедренном треугольнике углы при
основании равны.
Сумма углов, прилежащих боковой стороне
трапеции равна 180°.
21

22. Модуль «ГЕОМЕТРИЯ» №10 (1)

В
5
3
cos B
5
С
Найти АС.
А
ВС
cos B
АВ
⇒
ВС 3
АВ 5
Повторение (2)
⇒
ВС 3
По теореме Пифагора
2
2
2
2
АС АВ ВС 5 3 4
Ответ: 4.
22

23. Повторение

Косинус острого угла прямоугольного
треугольника равен отношению прилежащего
катета к гипотенузе
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
23

24. Модуль «ГЕОМЕТРИЯ» №10 (2)

15
tgA
8
В
15
С
Найти АВ.
Повторение (2)
А
ВС
tgA
АC
⇒
ВС 15
АC 8
⇒
AС 8
По теореме Пифагора
ÀB
ÀC 2 ÂÑ 2 8 2 15 2 17
Ответ: 17.
24

25. Повторение

Тангенс острого угла прямоугольного
треугольника равен отношению
противолежащего катета к прилежащему
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
25

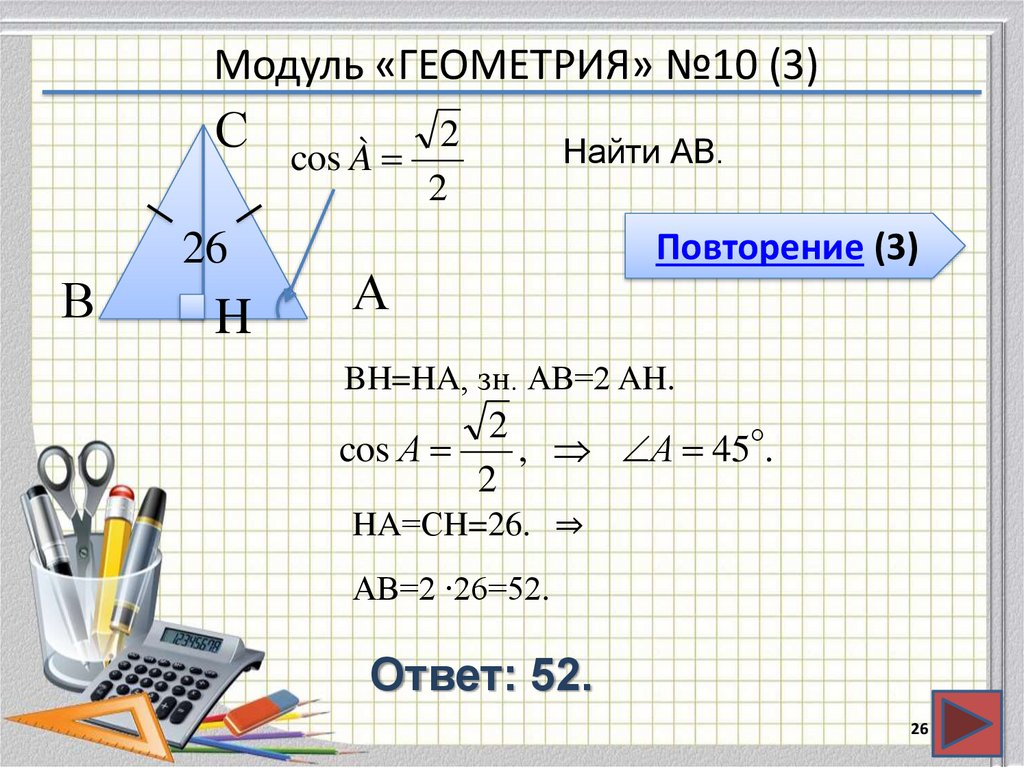
26. Модуль «ГЕОМЕТРИЯ» №10 (3)

С
В
26
H
2
cos À
2
Найти АВ.
А
Повторение (3)
BH=HA, зн. АВ=2 AH.
2
cos А
, А 45 .
2
HA=СH=26. ⇒
АВ=2 ∙26=52.
Ответ: 52.
26

27. Повторение

Высота в равнобедренном треугольнике,
проведенная к основанию, является и медианой
В прямоугольном треугольнике сумма острых
углов равна 90⁰
Если в треугольнике два угла равны, то такой
треугольник равнобедренный
27

28. Модуль «ГЕОМЕТРИЯ» №10 (4)

С
Найти CH.
78 3
Повторение (2)
А
В
H
BH=HA, зн. АH=½ AB= 39 3
По теореме Пифагора в ∆ACH
СH АC 2 AH 2 (78 3)2 (39 3)2 117
Ответ: 117.
28

29. Повторение

Высота в равнобедренном треугольнике,
проведенная к основанию, является и медианой
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
29

30. Модуль «ГЕОМЕТРИЯ» №10 (5)

С
Найти AB.
120⁰
Повторение (3)
25 3
В
H
А
Проведем высоту CH, получим ∆ВCH.
∠ВCH=60⁰ ⇒ ∠CВH=30⁰
1
⇒ CH 25 3
2
По теореме Пифагора в ∆BCH
1
2
2
2
BH BC CH (25 3 ) ( 25 3 ) 2 37,5
2
Ответ: 37,5.
30

31. Повторение

Высота в прямоугольном треугольнике,
проведенная к основанию является
биссектрисой и медианой
В прямоугольном треугольнике катет, лежащий
против угла в 30⁰, равен половине гипотенузы
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
31

32. Модуль «ГЕОМЕТРИЯ» №10 (6)

В
А
1
2
3
Е
С Дано: параллелограмм, BE –
биссектриса ∠B, P=10,
D АЕ:ЕD=1:3.
Найти: AD
∠1=∠3 как накрест лежащие при секущей ВЕ
∠3=∠2 так как ∠1=∠2 по условию ⇒ АВ=АЕ
Пусть АЕ=х, тогда АВ=х, ЕD=3х
Повторение (4)
Р=2∙(х+4х) ⇒ 2∙(х+4х)=10
5х=5
Х=1
AD=4∙1=4
Ответ: 4.
32

33. Повторение

Биссектриса – это луч, который делит угол
пополам
Периметр многоугольника – это сумма длин всех
сторон многоугольника
При пересечении двух параллельных прямых
накрест лежащие углы равны
Если два угла в треугольнике равны, то
треугольник - равнобедренный
33

34. Модуль «ГЕОМЕТРИЯ» №10 (7)

В
М
А 51
С
?
H
94
E
К
D
АВСD – трапеция, AH=51,
HD=94
Найти среднюю линию трапеции
Повторение (3)
Проведем СЕ⍊AD, получим ∆ABH=∆CED и
прямоугольник BCEH
⇒
AH=ЕD=51, BC=HE=HD-ED=94-51=43,
⇒ AD=AH+HE+ЕD= 51+94=145
AD BC
⇒
MK
2
145 43
MK
94
2
Ответ: 94.
34

35. Повторение

Если гипотенуза и катет одного прямоугольного
треугольника соответственно равны гипотенузе и
катету другого треугольника, то треугольники равны
Если отрезок точкой разделен на части, то его
длина равна сумме длин его частей
Средняя линия трапеции равна полусумме
оснований трапеции
35

36.

Книги по подготовке к ГИА
Модуль «Геометрия» содержит 8
заданий: в части 1 - 5 заданий, в части 2 - 3 задания.