ПРЕЗЕНТАЦИЯ ПО ГЕОМЕТРИИ

1.

БЕЗ ДОКАЗАТЕЛЬСТВА:
Предмет стереометрии. Основные фигуры в пространстве. Аксиомы стереометрии
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Основные фигуры в стереометрии: Точка, прямая, плоскость.
Аксиомы стереометрии
1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
Следствия из аксиом
1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
2. Через две пересекающиеся прямые проходит плоскость, и притом только одна

2.

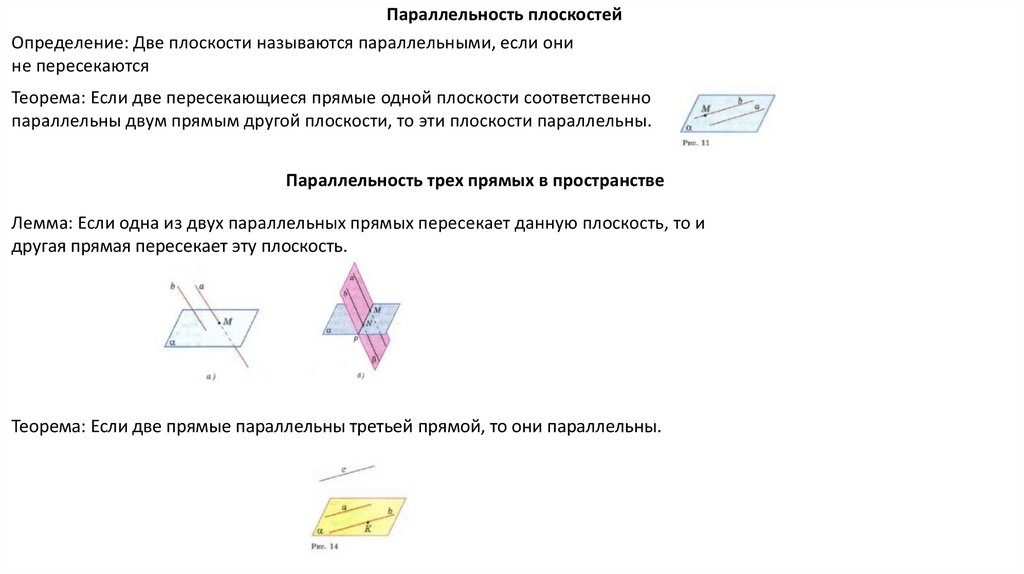
Параллельность плоскостей
Определение: Две плоскости называются параллельными, если они
не пересекаются
Теорема: Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Параллельность трех прямых в пространстве
Лемма: Если одна из двух параллельных прямых пересекает данную плоскость, то и
другая прямая пересекает эту плоскость.
Теорема: Если две прямые параллельны третьей прямой, то они параллельны.

3.

Тетраэдр
Тетраэдр - простейший многогранник, гранями
которого являются четыре треугольника
Содержит: 4 грани, 4 вершины и 6 ребер.
Параллеллепипед
Параллелепипед — это многогранник, ограниченный
шестью параллелограммами, расположенными
параллельно друг другу попарно.
Состоит из: 6 параллелограммов
или
12 ребер, 6 граней и 8 вершин
Свойство 1: Противоположные грани параллелепипеда параллельны и равны
(Две грани параллельны, если их плоскости параллельны)
Свойство 2: Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

4.

С ДОКАЗАТЕЛЬСТВОМ:
Параллельные прямые в пространстве
Определение: Две прямые в пространстве называются параллельными, если они лежат в одной
плоскости и не пересекаются.
Теорема: Через любую точку пространства, не лежащую на
данной прямой, проходит
прямая, параллельная данной, и притом только одна.

5.

Параллельность прямой и плоскости
Определение: Прямая и плоскость называются
параллельными, если они не имеют
общих точек
Взаимные расположения прямой и плоскости:
1. Прямая лежит в плоскости (рис. а)
2. Прямая и плоскость имеют только одну общую точку, т.е. пересекаются (рис. б)
3. Прямая и плоскость не имеют ни одной общей точки
Свойство 1: Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает
эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Свойство 2: Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо
также параллельна данной плоскости, либо лежит в этой плоскости
Теорема: Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой
плоскости, то она параллельна данной плоскости.

6.

Скрещивающиеся прямые
Определение: Две прямые называются скрещивающимися, если они
не лежат в одной плоскости.
Взаимное расположение двух прямых в пространстве:
1. Прямые пересекаются (1 общая точка)
2. Прямые параллельны (в одной плоскости, не пересекаются)
3. Прямые скрещиваются (не лежат в одной плоскости)
Теоремы:
1. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость
в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
2. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная
другой прямой, и притом только одна.

7.

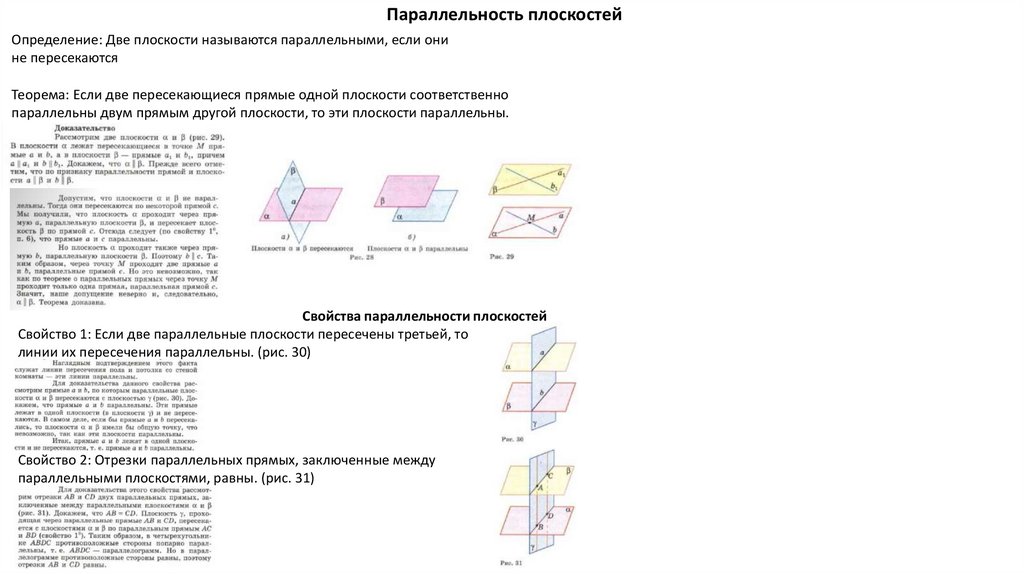
Параллельность плоскостей
Определение: Две плоскости называются параллельными, если они
не пересекаются
Теорема: Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Свойства параллельности плоскостей
Свойство 1: Если две параллельные плоскости пересечены третьей, то
линии их пересечения параллельны. (рис. 30)
Свойство 2: Отрезки параллельных прямых, заключенные между
параллельными плоскостями, равны. (рис. 31)

8.

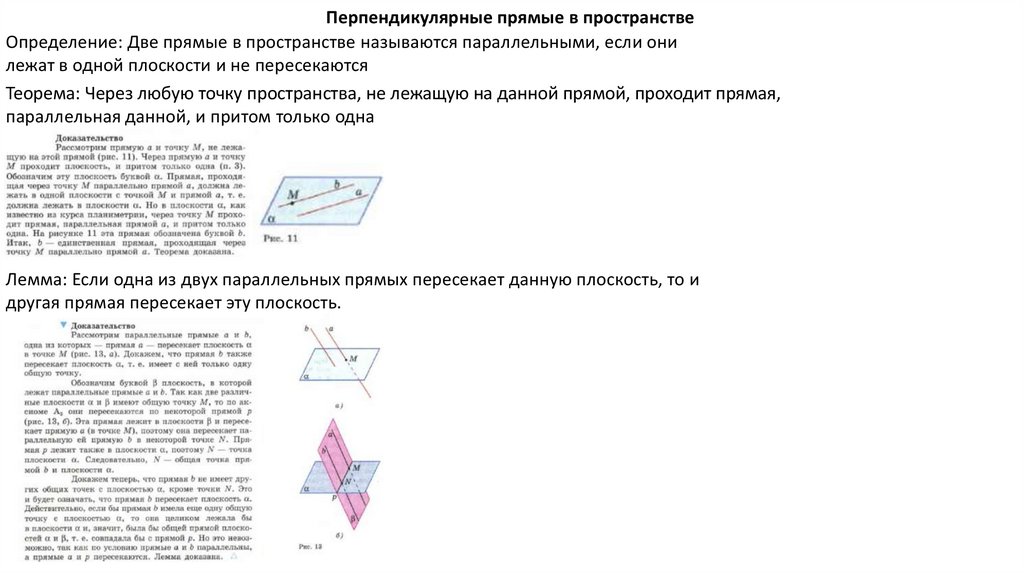
Перпендикулярные прямые в пространстве
Определение: Две прямые в пространстве называются параллельными, если они
лежат в одной плоскости и не пересекаются
Теорема: Через любую точку пространства, не лежащую на данной прямой, проходит прямая,
параллельная данной, и притом только одна
Лемма: Если одна из двух параллельных прямых пересекает данную плоскость, то и
другая прямая пересекает эту плоскость.