Аксиомы стереометрии

1.

Аксиомы
стереометрии
1

2.

Геометрия
Планиметрия
Стереометрия
stereos
объемный,
пространственный
2

3.

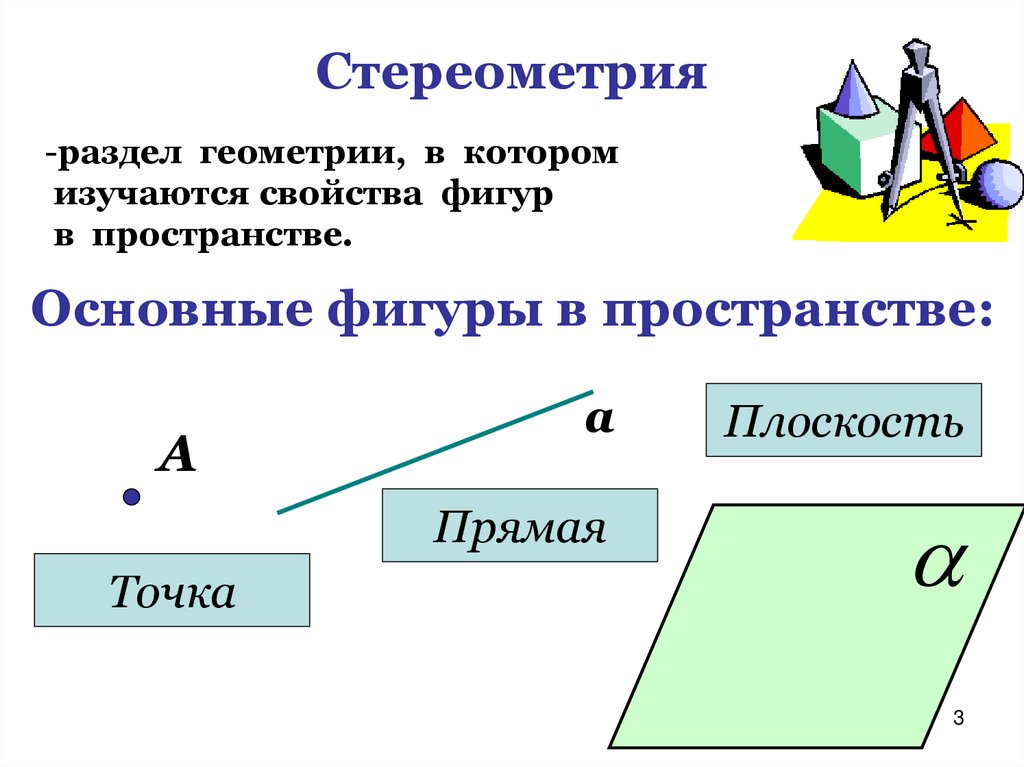
Стереометрия
-раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка
а
Плоскость
Прямая
3

4.

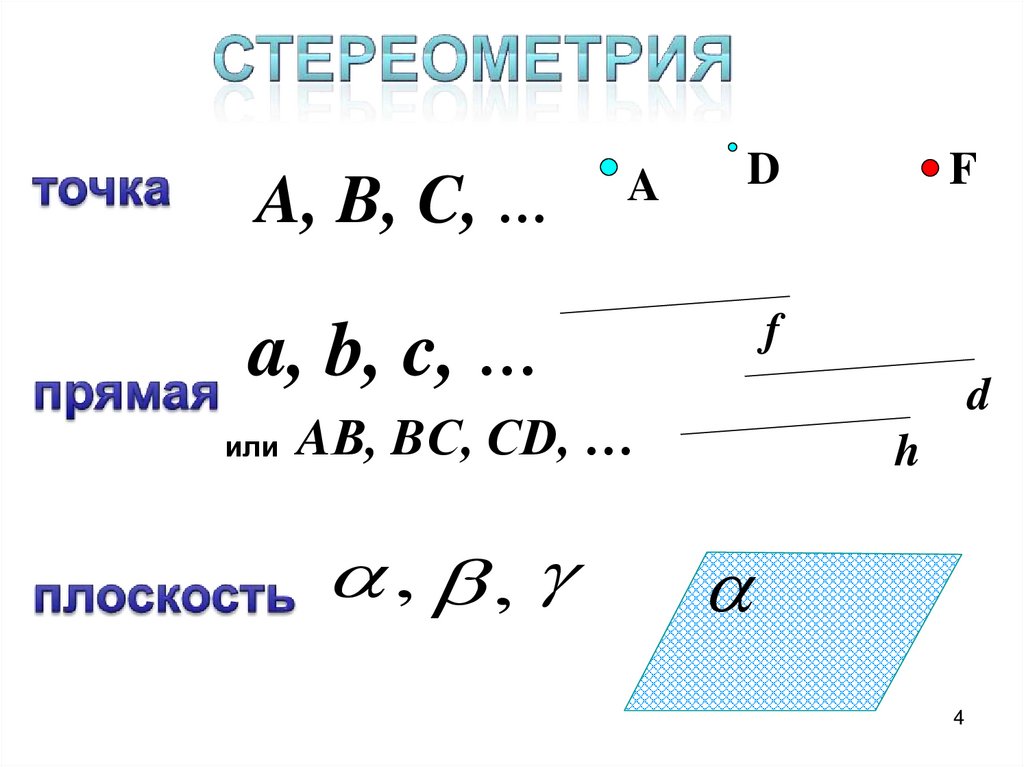
A, B, C, …
A
D
f
a, b, c, …
или
d
AВ, BС, CD, …
, ,
F
h
4

5.

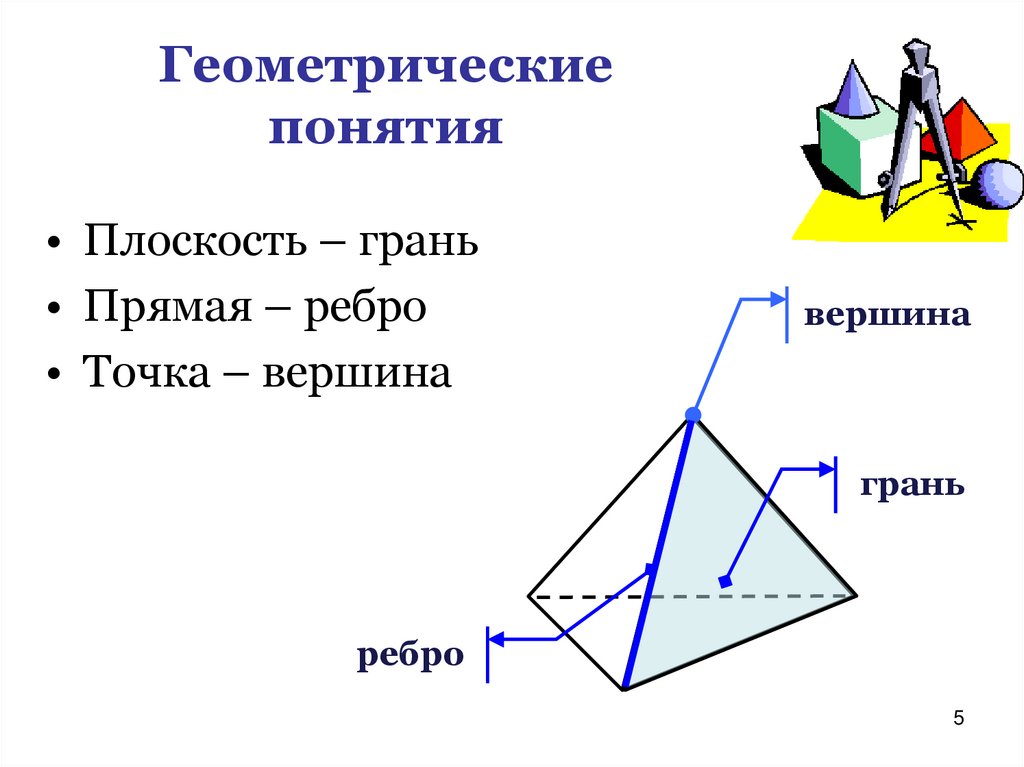
Геометрические
понятия
• Плоскость – грань
• Прямая – ребро
• Точка – вершина
вершина
грань
ребро
5

6.

Аксиома
(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства
6

7.

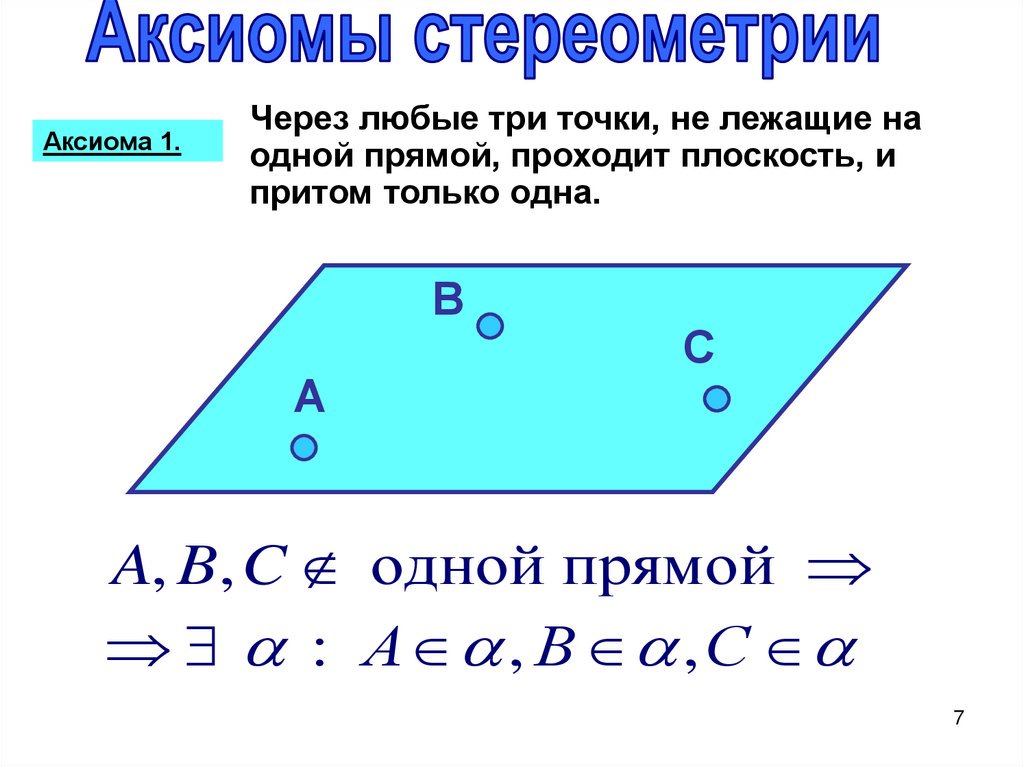
Аксиома 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
В
А
С
A, B, C одной прямой
! : А , В , С
7

8.

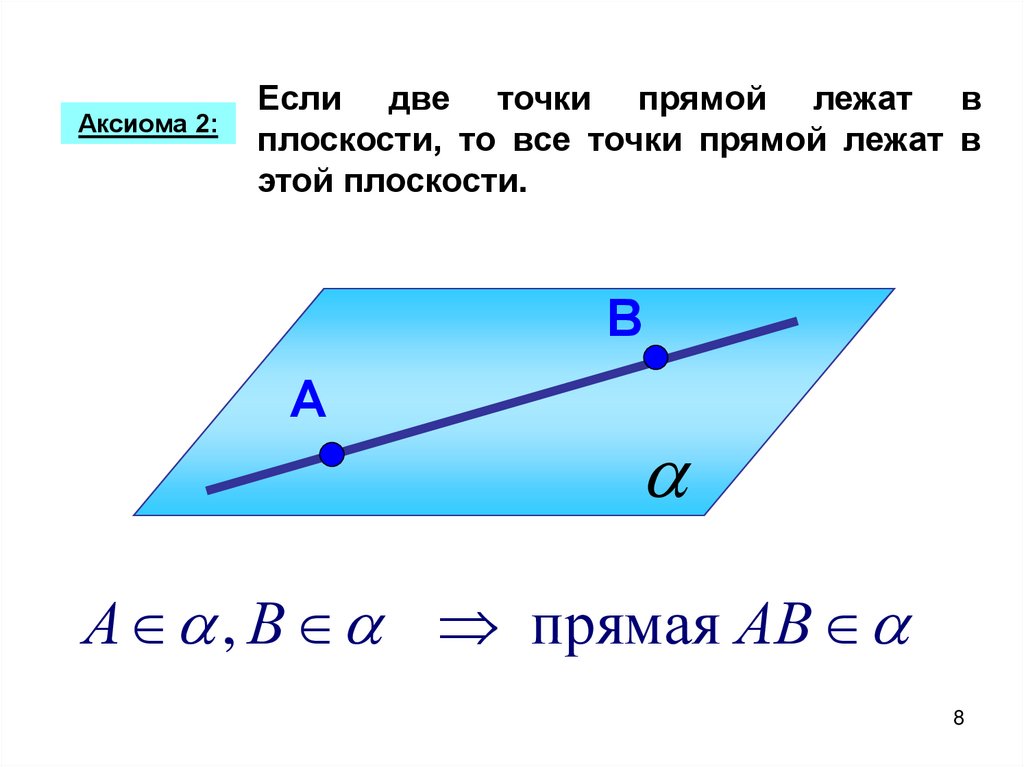
Аксиома 2:
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости.
В
А
А , В прямая АВ
8

9.

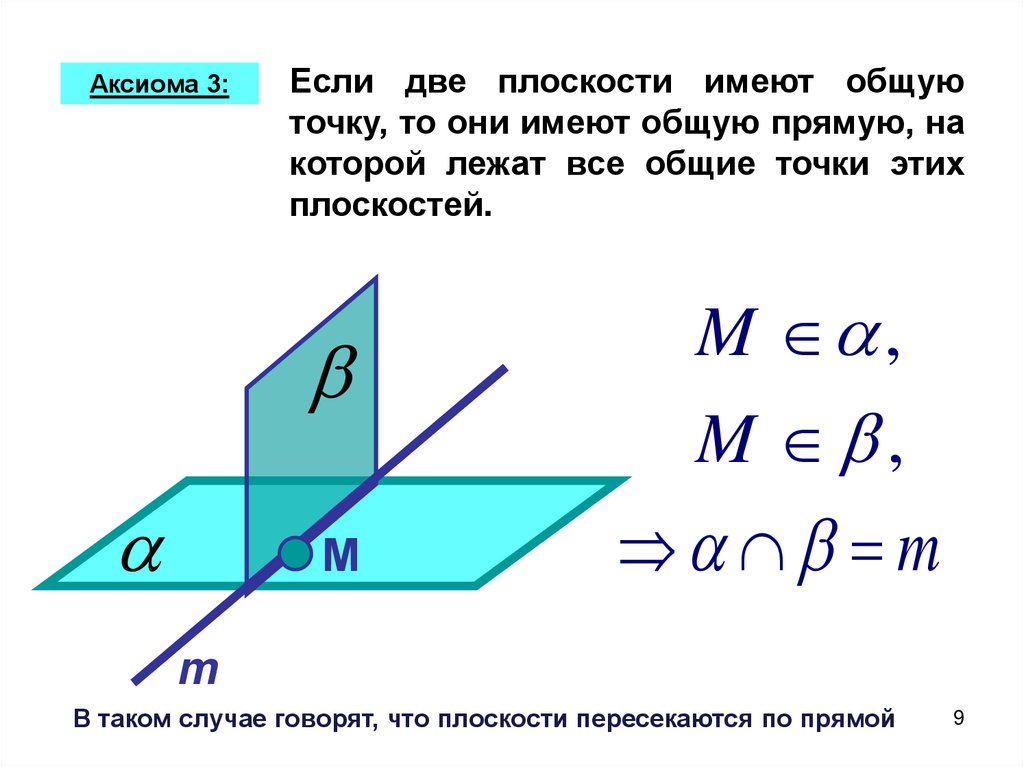
Аксиома 3:
Если две плоскости имеют общую
точку, то они имеют общую прямую, на
которой лежат все общие точки этих
плоскостей.
М
M ,
M ,
m
m
В таком случае говорят, что плоскости пересекаются по прямой
9

10.

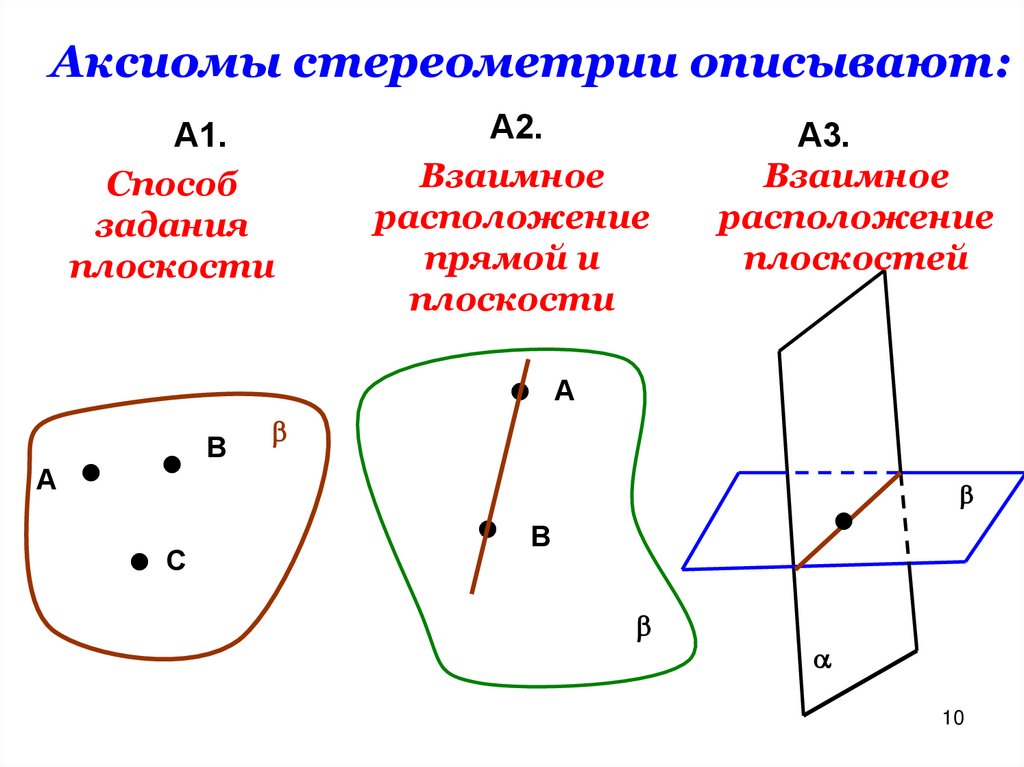
Аксиомы стереометрии описывают:
А1.
Способ
задания
плоскости
А2.
Взаимное
расположение
прямой и
плоскости
А3.
Взаимное
расположение
плоскостей
А
В
А
С
В
10

11.

Способы задания плоскости
2. Можно
3. Можно
1. Плоскость
провести через провести через
можно провести
прямую и не
две
через три
лежащую на ней пересекающиеся
точки.
точку.
прямые.
Аксиома 1
Теорема 1
Теорема 2
11

12.

Взаимное расположение двух прямых в
пространстве
1. Лежат в одной плоскости
пересекаются
b
параллельны
b
а
а
2. Не лежат в одной плоскости
b
скрещиваются
а
12

13.

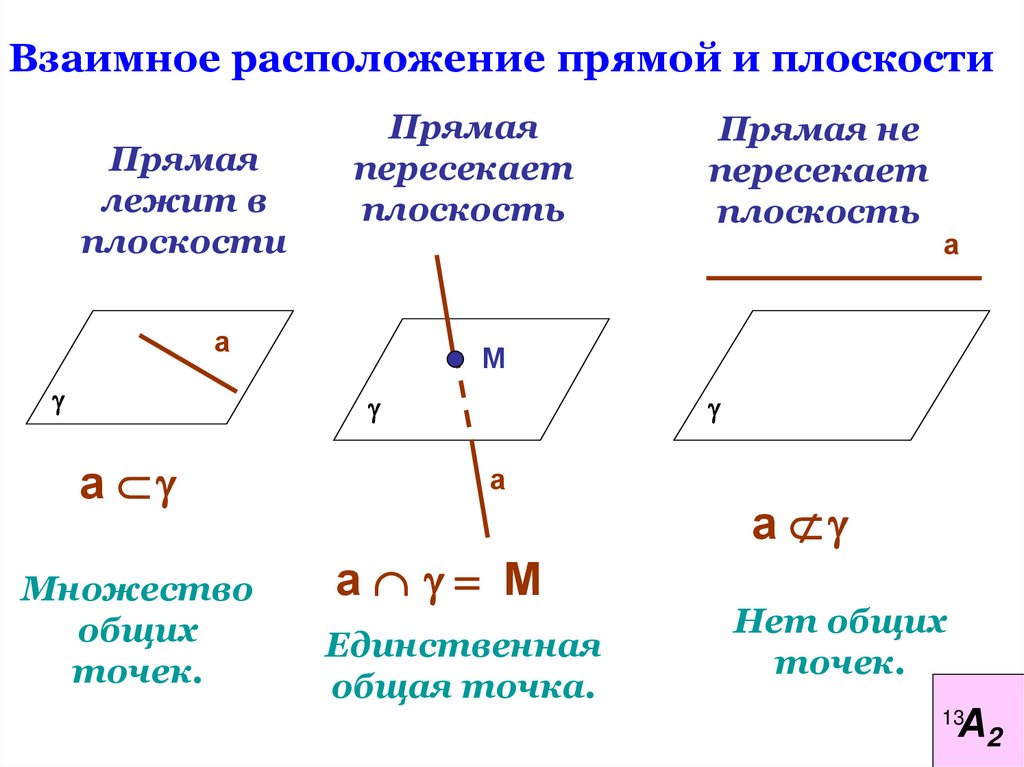
Взаимное расположение прямой и плоскости
Прямая
лежит в
плоскости
Прямая
пересекает
плоскость
а
Множество
общих
точек.
а
М
а
Прямая не
пересекает
плоскость
а
а М
Единственная
общая точка.
а
Нет общих
точек.
А2
13

14.

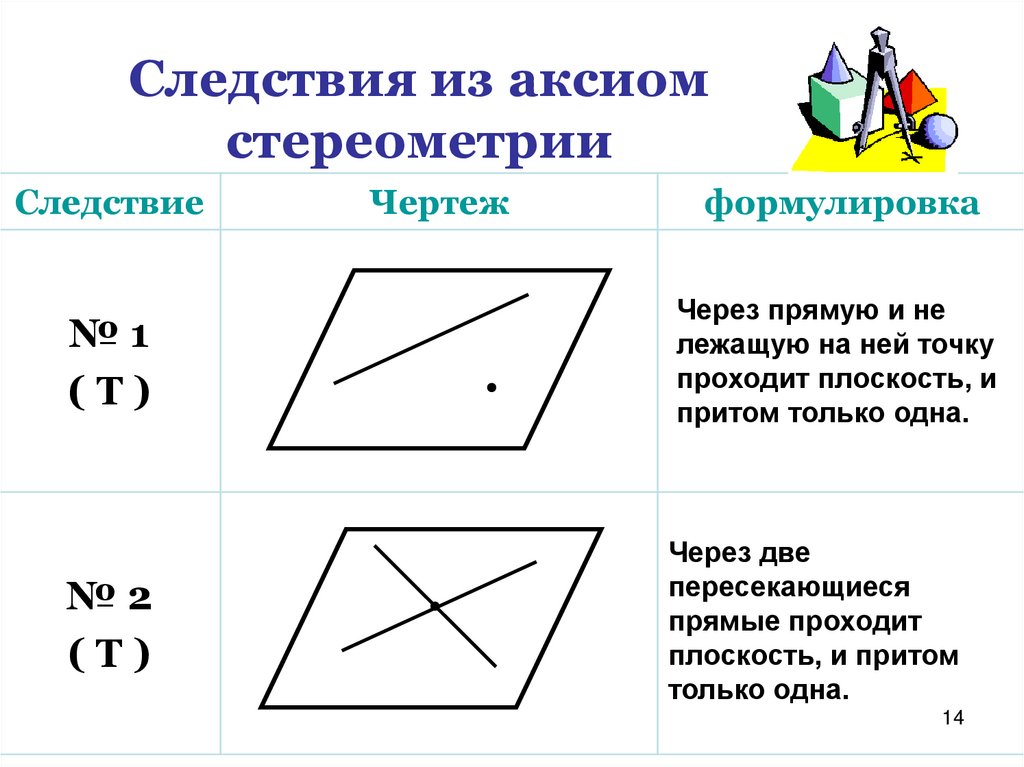
Следствия из аксиом
стереометрии
Следствие
Чертеж
формулировка
№1
(Т)
Через прямую и не
лежащую на ней точку
проходит плоскость, и
притом только одна.
№2
(Т)
Через две
пересекающиеся
прямые проходит
плоскость, и притом
только одна.
14

15.

Домашнее
задание
Выучить аксиомы
и следствия из них
15

16.

Параллельность
прямой и плоскости.
Параллельность
плоскостей
16

17.

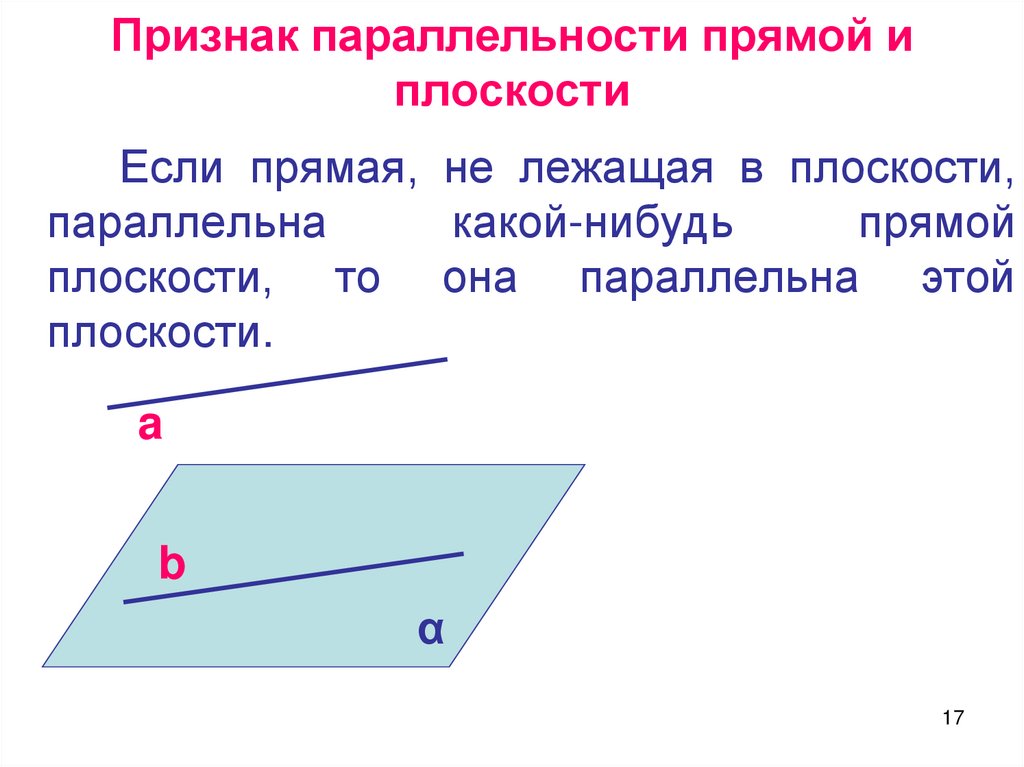
Признак параллельности прямой и
плоскости
Если прямая, не лежащая в плоскости,
параллельна
какой-нибудь
прямой
плоскости, то она параллельна этой
плоскости.
a
b
α
17

18.

Параллельность плоскостей
ОПРЕДЕЛЕНИЕ
Плоскости называются параллельными,
если они не имеют общих точек.
ПРИЗНАК
Если две пересекающиеся прямые одной
плоскости параллельны соответственно
двум прямым другой плоскости, то
плоскости параллельны.
18

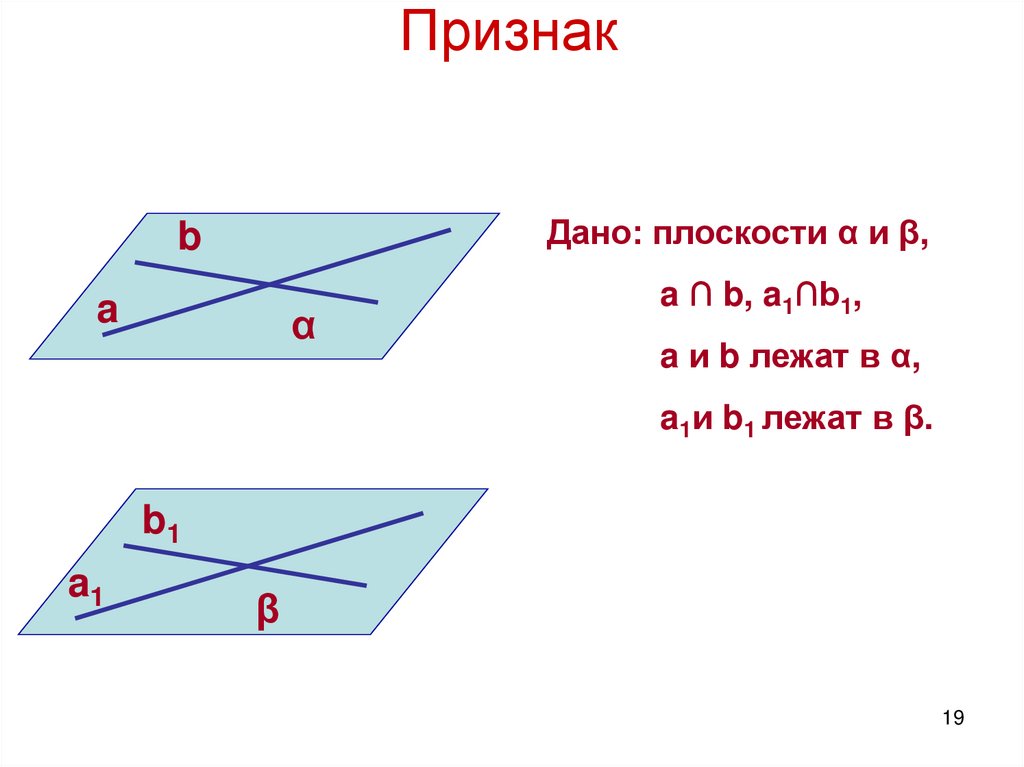
19.

Признак
Дано: плоскости α и β,
b
a
α
a ∩ b, a1∩b1,
a и b лежат в α,
a1и b1 лежат в β.
b1
a1
β
19

20.

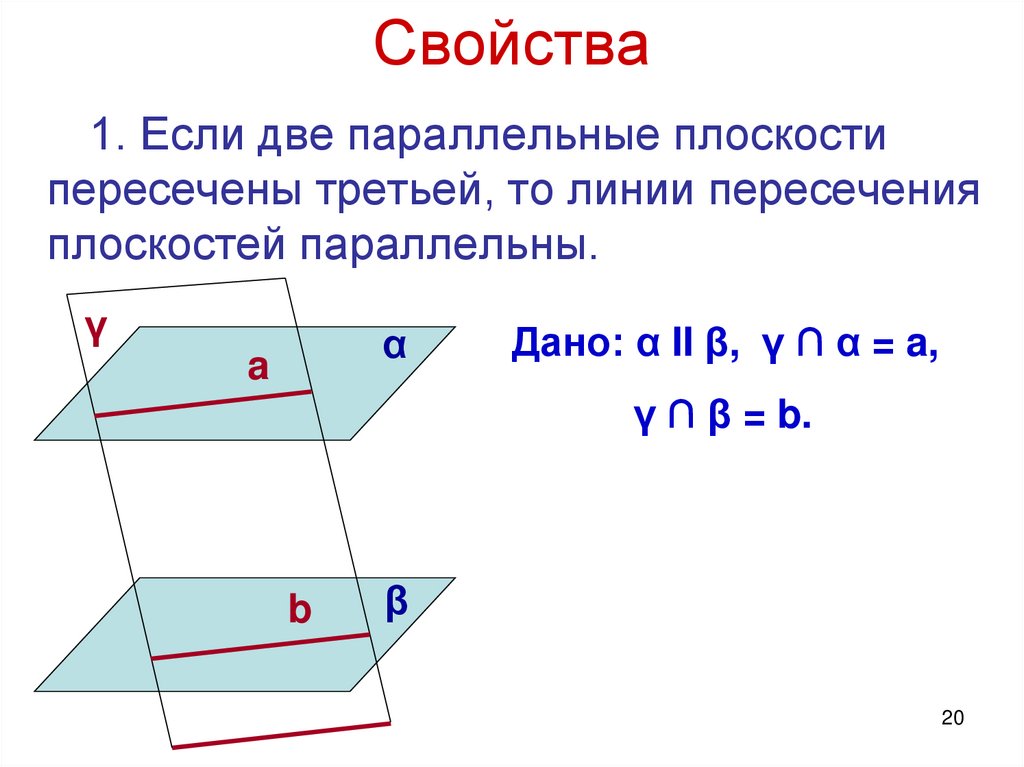
Свойства
1. Если две параллельные плоскости
пересечены третьей, то линии пересечения
плоскостей параллельны.
γ
α
a
Дано: α II β, γ ∩ α = a,
γ ∩ β = b.
b
β
20

21.

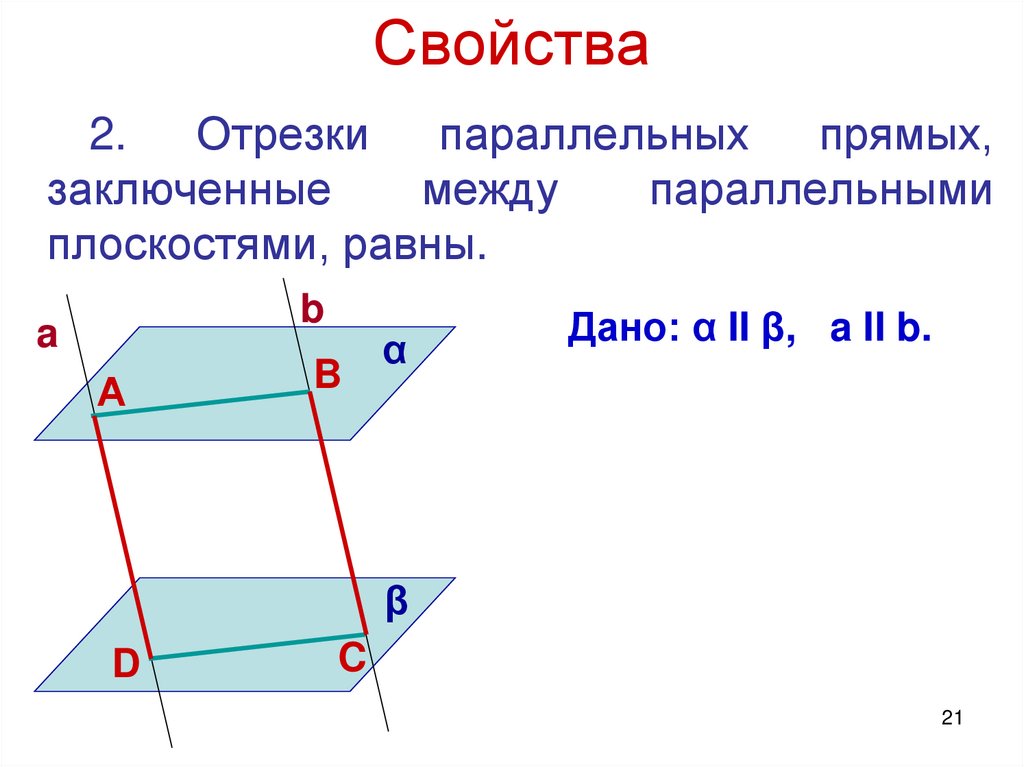
Свойства
2.
Отрезки
параллельных
прямых,
заключенные
между
параллельными
плоскостями, равны.
b
a
А
B
α
Дано: α II β, a II b.
β
D
C
21

22.

Свойства
3. Если прямая пересекает одну из
параллельных
плоскостей,
то
она
пересекает и другую.
4. Если плоскость пересекает одну из
параллельных
плоскостей,
то
она
пересекает и вторую плоскость.
5. В пространстве через точку, не
лежащую на данной плоскости, можно
провести
плоскость,
параллельную
данной, притом только одну.
22

23.

Домашнее задание
• Решить задачи 17 и 18
23