Ориентирование линий на местности

1.

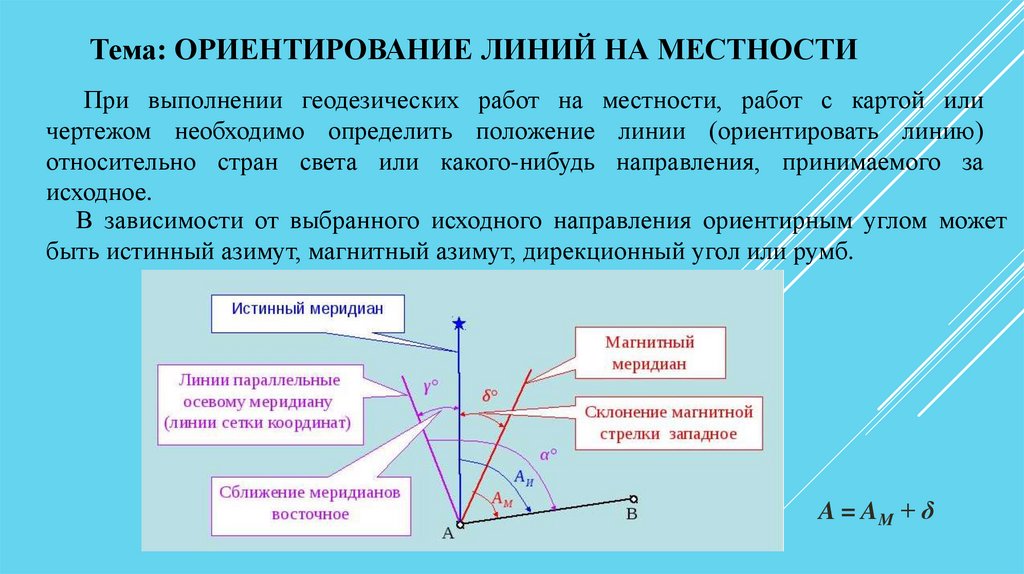
Тема: ОРИЕНТИРОВАНИЕ ЛИНИЙ НА МЕСТНОСТИ
При выполнении геодезических работ на местности, работ с картой или
чертежом необходимо определить положение линии (ориентировать линию)
относительно стран света или какого-нибудь направления, принимаемого за
исходное.
В зависимости от выбранного исходного направления ориентирным углом может
быть истинный азимут, магнитный азимут, дирекционный угол или румб.
A = AM + δ

2.

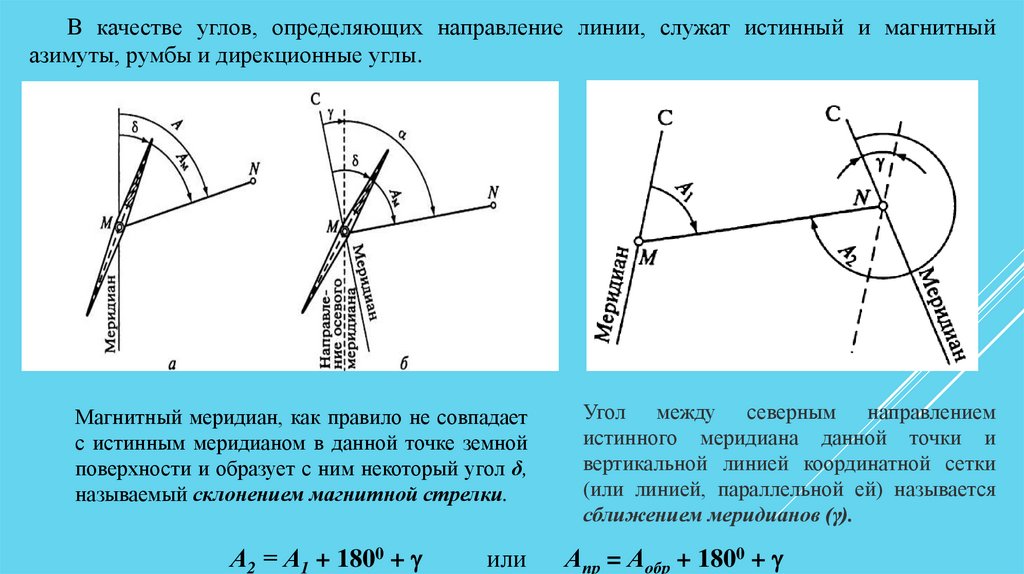
В качестве углов, определяющих направление линии, служат истинный и магнитный
азимуты, румбы и дирекционные углы.
Магнитный меридиан, как правило не совпадает
с истинным меридианом в данной точке земной
поверхности и образует с ним некоторый угол δ,
называемый склонением магнитной стрелки.
А2 = А1 + 1800 +
или
Угол между северным направлением
истинного меридиана данной точки и
вертикальной линией координатной сетки
(или линией, параллельной ей) называется
сближением меридианов (γ).
Апр = Аобр + 1800 +

3.

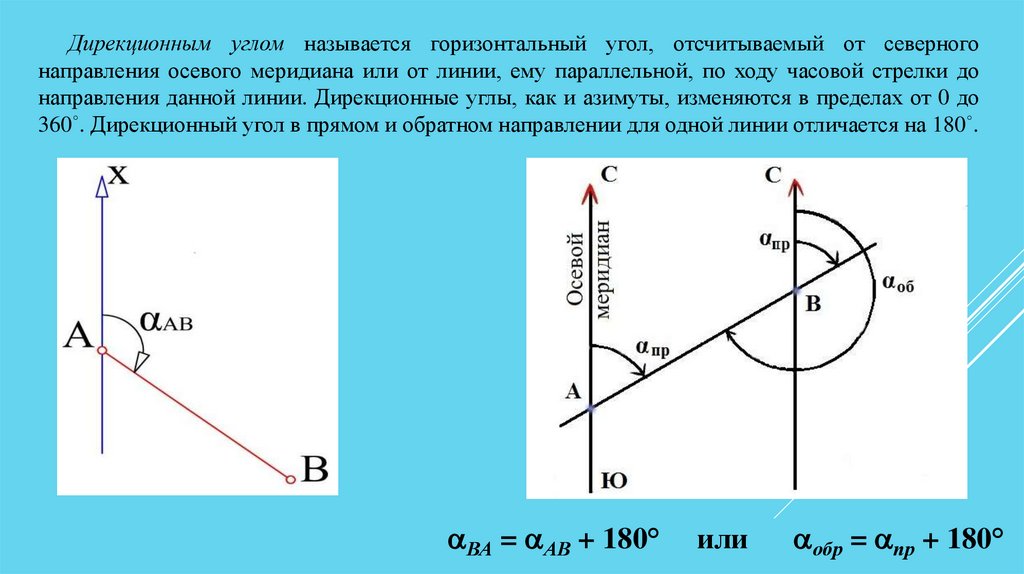
Дирекционным углом называется горизонтальный угол, отсчитываемый от северного
направления осевого меридиана или от линии, ему параллельной, по ходу часовой стрелки до
направления данной линии. Дирекционные углы, как и азимуты, изменяются в пределах от 0 до
360˚. Дирекционный угол в прямом и обратном направлении для одной линии отличается на 180˚.
ВА = АВ + 180°
или
обр = пр + 180°

4.

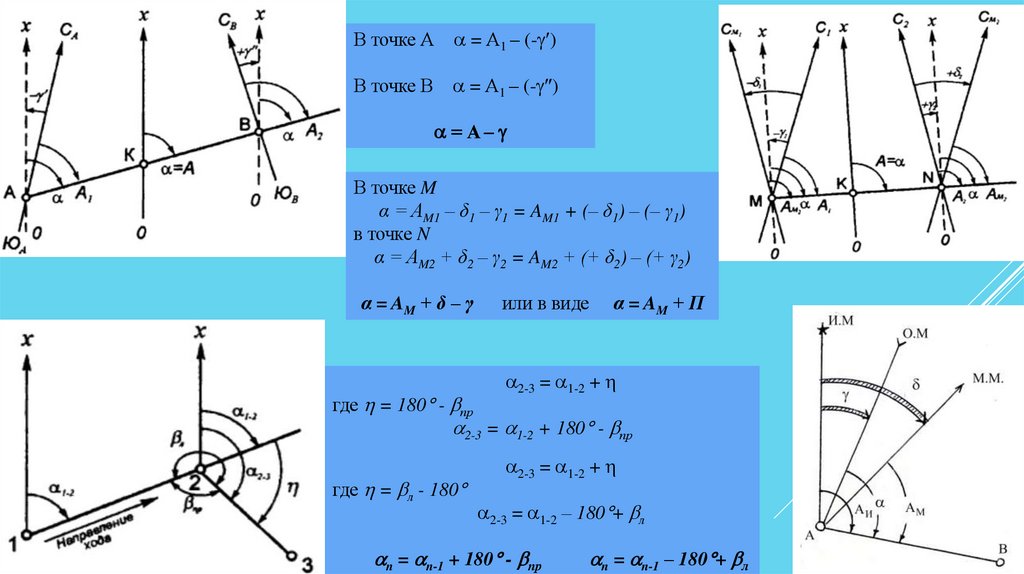
В точке А = А1 – (- )
В точке В = А1 – (- )
= А–
В точке M
α = AM1 – δ1 – γ1 = AM1 + (– δ1) – (– γ1)
в точке N
α = AM2 + δ2 – γ2 = AM2 + (+ δ2) – (+ γ2)
α = AM + δ – γ
где = 180 - пр
или в виде
α = AM + П
2-3 = 1-2 +
2-3 = 1-2 + 180 - пр
где = л - 180
2-3 = 1-2 +
2-3 = 1-2 – 180 + л
n = n-1 + 180 - пр
n = n-1 – 180 + л

5.

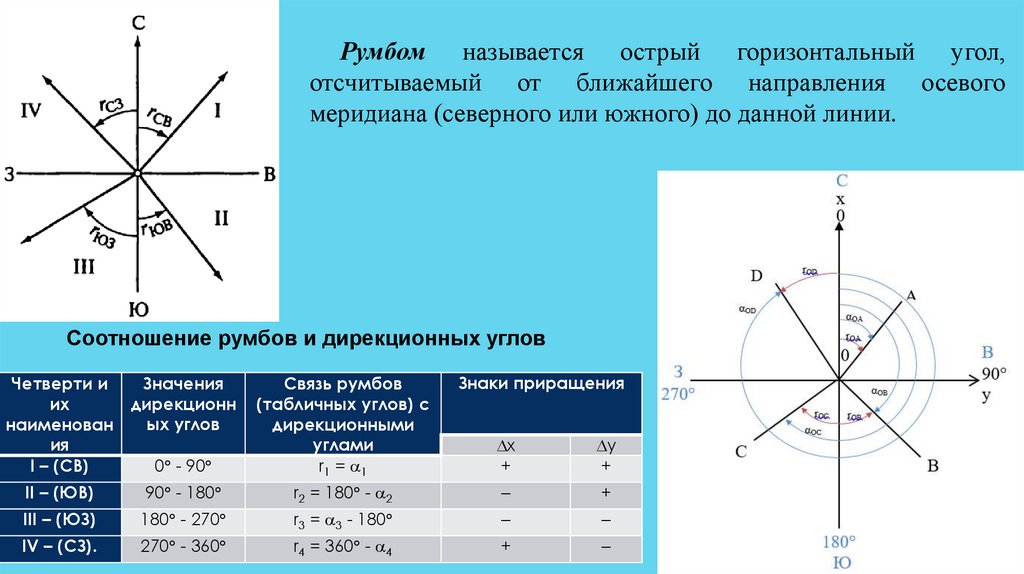
Румбом называется острый горизонтальный угол,
отсчитываемый от ближайшего направления осевого
меридиана (северного или южного) до данной линии.
Соотношение румбов и дирекционных углов
Четверти и
Значения
их
дирекционн
ых углов
наименован
ия
I – (СВ)
0 - 90
Связь румбов
(табличных углов) с
дирекционными
углами
r 1 = 1
Знаки приращения
х
+
у
+
II – (ЮВ)
90 - 180
r2 = 180 - 2
–
+
III – (ЮЗ)
180 - 270
r3 = 3 - 180
–
–
IV – (СЗ).
270 - 360
r4 = 360 - 4
+
–

6.

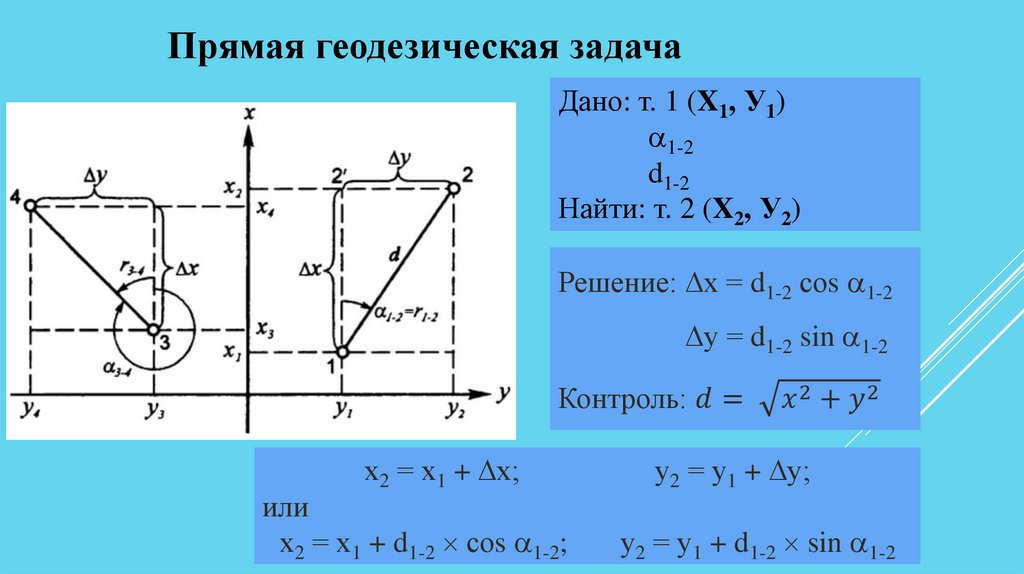
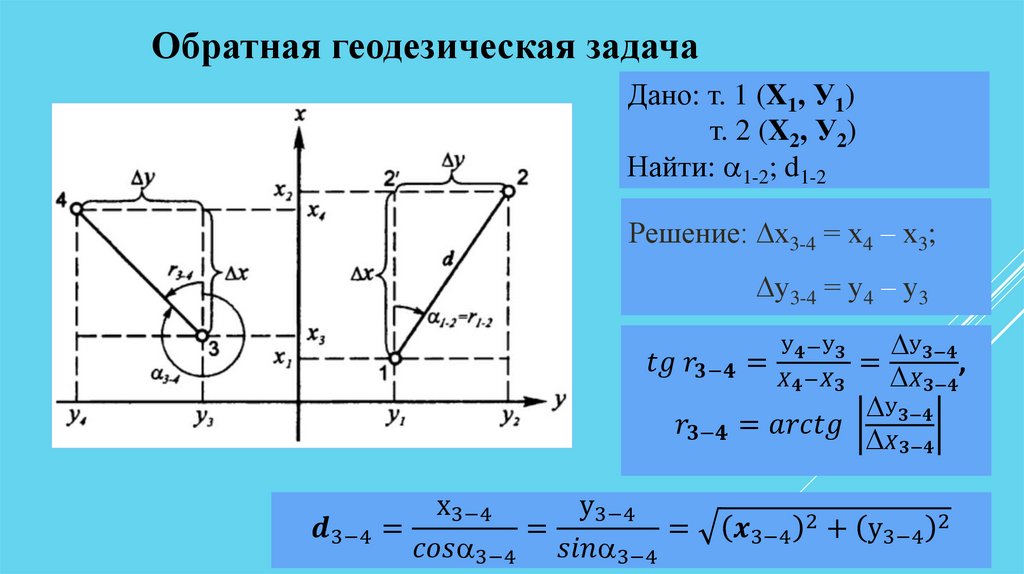
Прямая геодезическая задача
Дано: т. 1 (X1, У1)
1-2
d1-2
Найти: т. 2 (X2, У2)
Решение: х = d1-2 соs 1-2
у = d1-2 sin 1-2
Контроль: