Похожие презентации:
Ориентирование направлений
1. Тема 1.3. Ориентирование направлений
1.2.
3.
4.
Ориентирующие углы
Ориентирование линий по истинному и
магнитному меридиану
Ориентирование линий относительно оси
ОХ зональной системы плоских
прямоугольных координат.
Прямая и обратная геодезические задачи
2. 1. Ориентирующие углы
Ориентировать линию местности значит найти её направление относительнокакого-либо
другого
направления,
принимаемого за исходное.
Горизонтальный угол между исходным
направлением и
и ориентируемой линией
называется ориентирным углом.
2
3.
Начальноенаправление
Ориентирный
угол
Истинный
(географический)
меридиан
Истинный азимут, А (Аи)
Магнитный меридиан
Магнитный азимут, Ам
Осевой меридиан (ось ОХ)
Дирекционный угол,
α
Румб, r
3
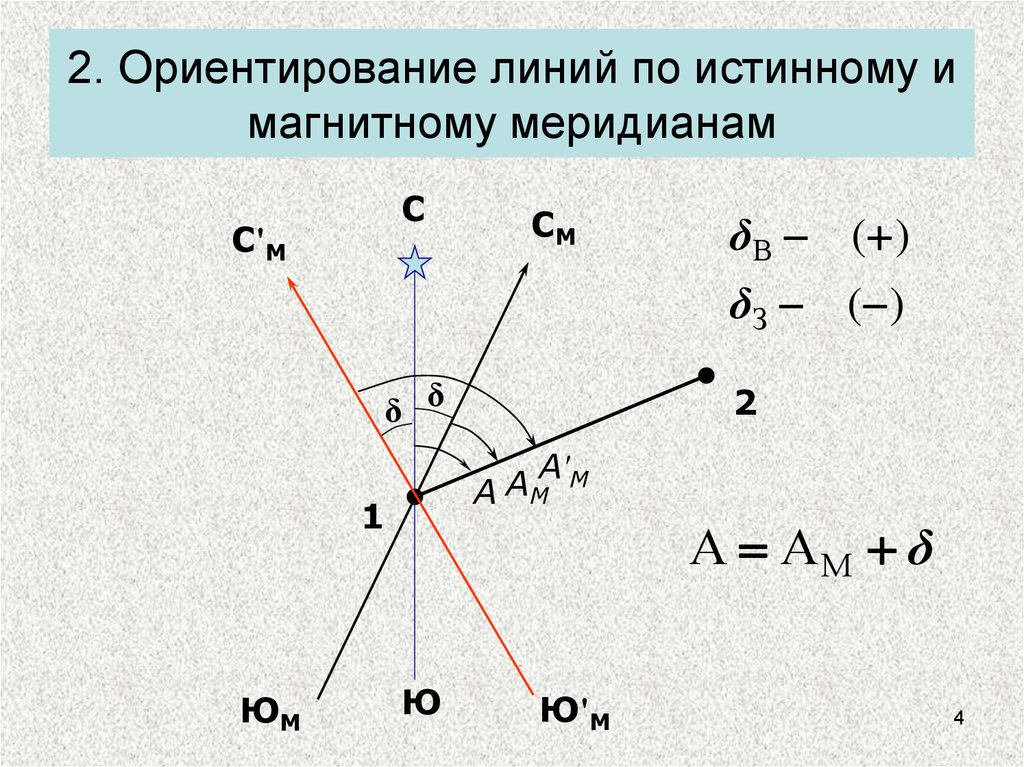
4. 2. Ориентирование линий по истинному и магнитному меридианам
СС'М
СМ
δВ ( )
δЗ ( )
δ δ
А'М
А
А М
1
ЮМ
2
А АМ δ
Ю
Ю'М
4
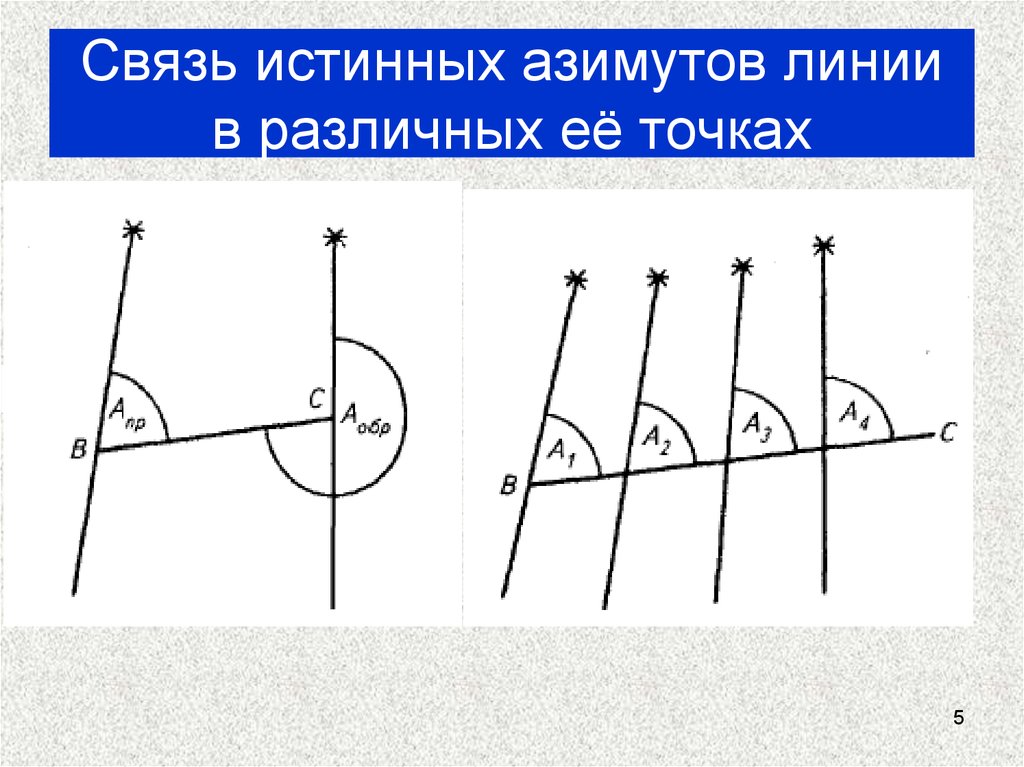
5. Связь истинных азимутов линии в различных её точках
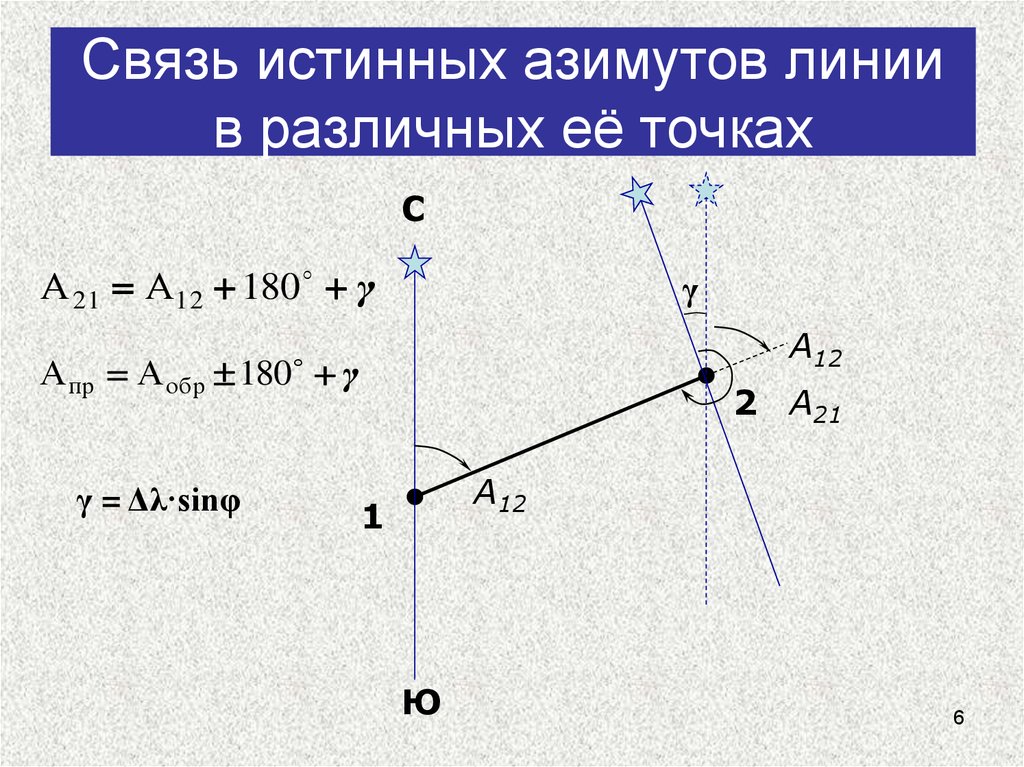
56. Связь истинных азимутов линии в различных её точках
СА 21 А12 180 γ
γ
А12
А пр А обр 180 γ
γ = Δλ·sinφ
2 А21
А12
1
Ю
6
7. 3. Ориентирование линий относительно оси ОХ зональной системы плоских прямоугольных координат
Сα 21 α12 180
Х
α12
αпр αобр 180
2 α21
α12
1
Ю
7
8. Связь дирекционного угла с истинным азимутом
γВ( )
γЗ
( )
α А γ
8
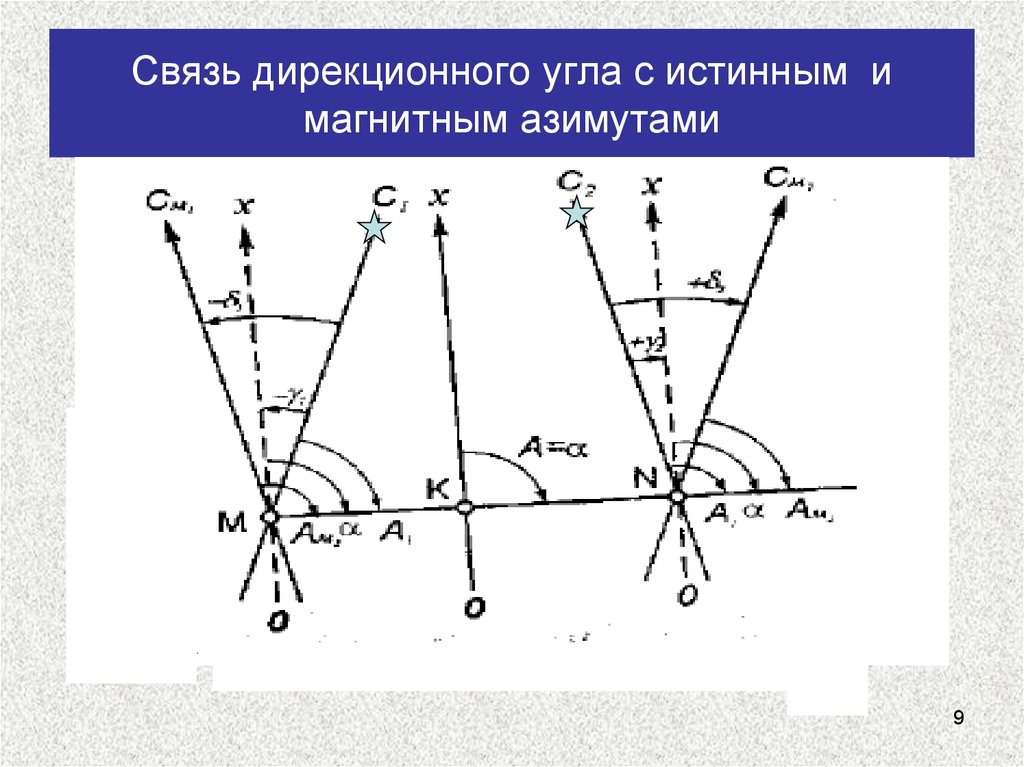
9. Связь дирекционного угла с истинным и магнитным азимутами
910. Связь дирекционного угла с истинным и магнитным азимутами
В точке МВ точке N
α А М1 δ1 γ1 А М1 ( δ1 ) ( γ1 )
α А М 2 δ2 γ 2 А М 2 ( δ2 ) ( γ 2 )
α АМ δ γ
α АМ Π
Π δ γ
10
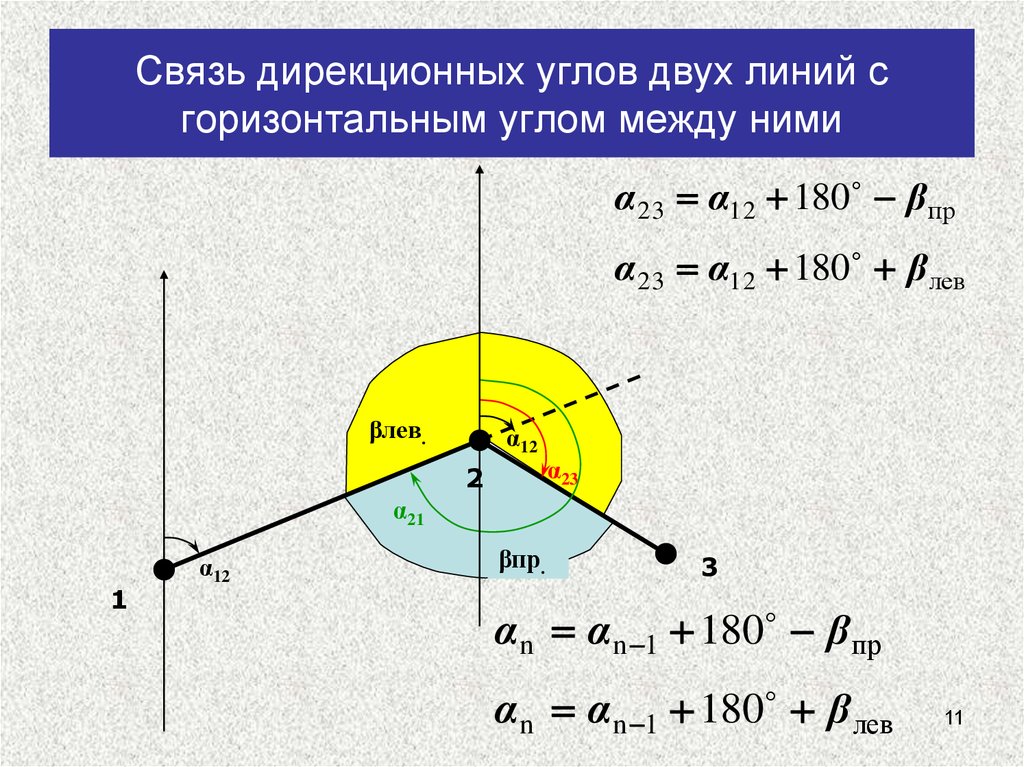
11. Связь дирекционных углов двух линий с горизонтальным углом между ними
α 23 α12 180 β прα 23 α12 180 β лев
βлев.
α12
2
α23
α21
1
α12
βпр.
3
α n α n 1 180 β пр
α n α n 1 180 β лев
11
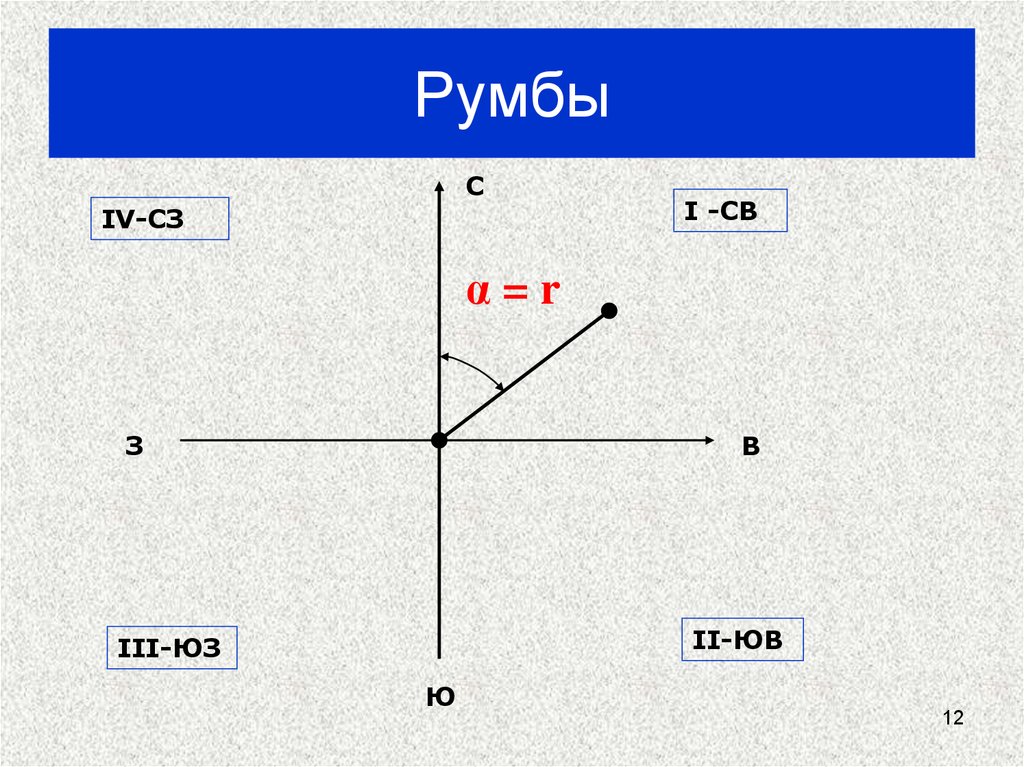
12. Румбы
СIV-СЗ
I -СВ
α=r
З
В
II-ЮВ
III-ЮЗ
Ю
12
13. Румбы
СI -СВ
IV-СЗ
З
α
r
В
r = 1800 - α
II-ЮВ
III-ЮЗ
Ю
13
14. Румбы
СIV-СЗ
З
r = α - 1800
α
I -СВ
В
r
II-ЮВ
III-ЮЗ
Ю
14
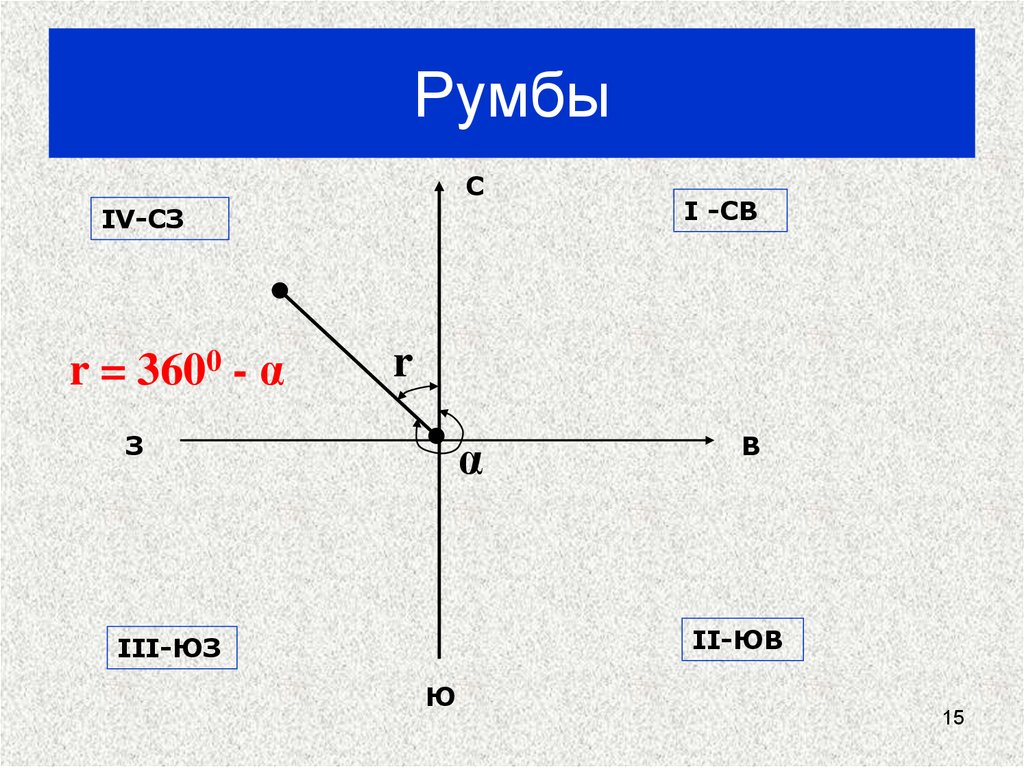
15. Румбы
СIV-СЗ
r = 3600 - α
I -СВ
r
З
α
В
II-ЮВ
III-ЮЗ
Ю
15
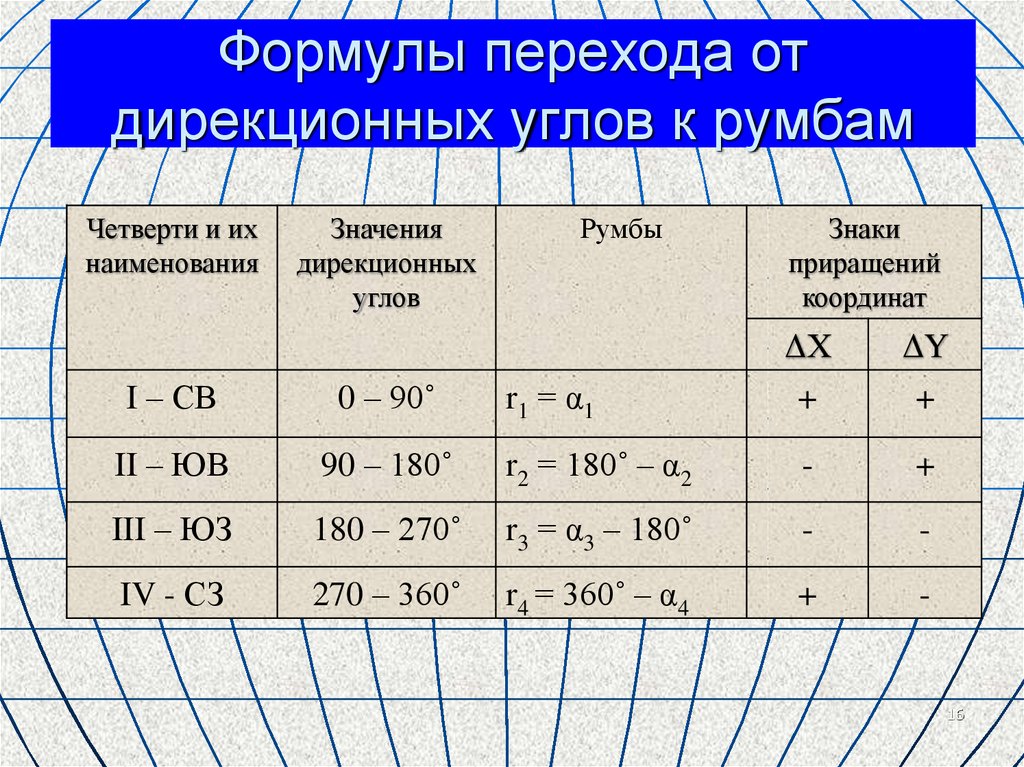
16. Формулы перехода от дирекционных углов к румбам
Четверти и ихнаименования
Значения
дирекционных
Дирекционныеуглов
углы,
Румбы
Знаки
приращений
координат
ΔХ
ΔY
r 1 = α1
+
+
I – СВ
0 – 90˚
II – ЮВ
90 – 180˚
r2 = 180˚ – α2
-
+
III – ЮЗ
180 – 270˚
r3 = α3 – 180˚
-
-
IV - СЗ
270 – 360˚
r4 = 360˚ – α4
+
-
16
17. Прямая геодезическая задача на плоскости
Дано: координаты точки А - X YА,
A
дирекционный угол линии АВ – αАВ
горизонтальное проложение линии АВ - dAB
Найти: координаты точки В - X Y
В,
В
17
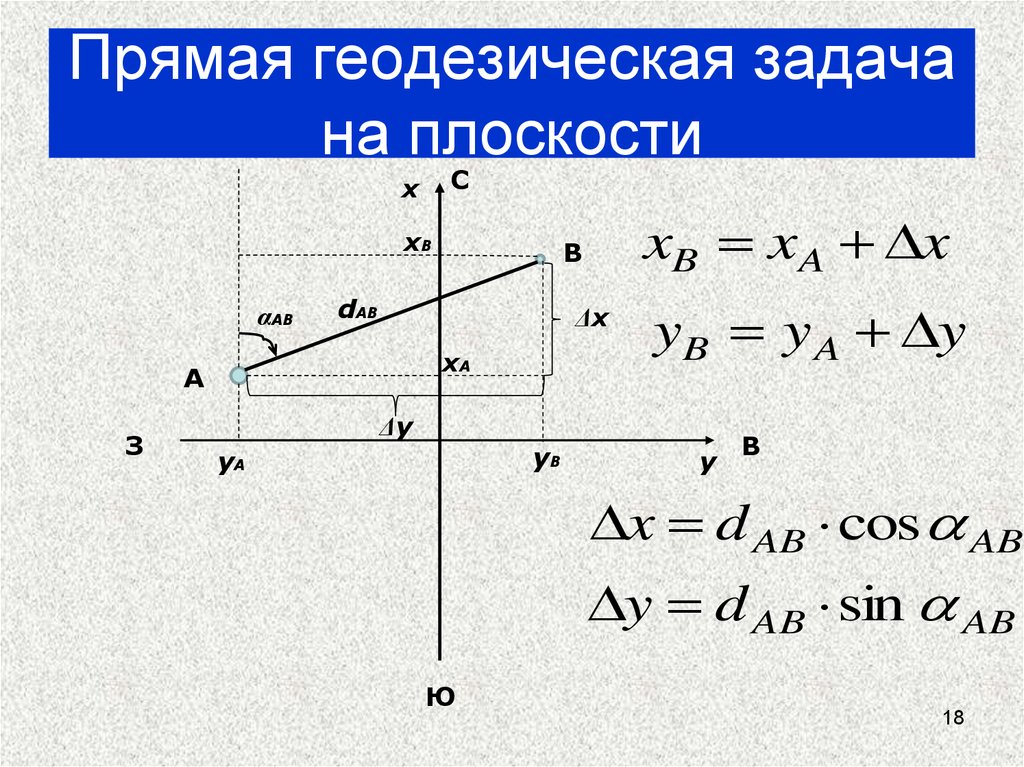
18. Прямая геодезическая задача на плоскости
Сx
xB
αAB
dAB
Δx
xA
A
З
xB xA x
B
yB y A y
Δy
yB
yA
y
В
x d AB cos AB
y d AB sin AB
Ю
18
19. Числовой пример:
• Дано: X = 501,234 м; Y = -90,651 м;А
A
• αАВ = 87º50'12"; dAB = 99,541 м.
Решение:
x 99,541 cos 87 50'12' ' 99,541 0,037748 3,758 м
y 99,541 sin 87 50'12' ' 99,541 0,99929 99,470 м
xB 501,234 3,758 504,992 м
yB 90,651 99,470 8,819 м
19
20. Обратная геодезическая задача на плоскости
Дано: координаты точки А - X YА,
A
координаты точки В - XВ, YВ
Найти:
дирекционный угол линии АВ – αАВ
горизонтальное проложение линии АВ - dAB
20
21. Обратная геодезическая задача на плоскости
xС
xB
αAB
dAB
Δx
tgrAB
xA
A
З
B
x xB x A
y yB y A
Δy
yB
yA
y
yB y A
y
xB x A
x
В
d AB x y
x
y
cos AB sin AB
2
d AB
Ю
2
21
22. Числовой пример:
• Дано: X = 501,234 м; Y = -90,651 м;А
A
XВ = 278,958 м; YВ = 26,777 м.
Решение:
rAB
x 278,958 501,234 222,276 м
y 26,777 ( 90,651) 117,428 м
117,428
arctg
7,847411 27 50'51' '
222,276
rAB 27 50'51' ' ( ЮВ)
d AB
Контроль:
АВ 180 27 50'51' ' 152 09'09' '
( 222,276) 2 117,4282 251,388 м
d AB
222,276
117,428
251,388 м
0,884194 0,467119
22













 География
География








