Сопротивление материалов

1. Прикладная механика Раздел: Сопротивление материалов

Лекция 2
Преподаватель: доцент,
Кандидат технических наук,
Костюк Елена Геннадиевна

2.

Положительные рассматриваемой
нормальные напряжения
• При анализе напряжений в 1.
окрестности
направлены в сторону внешней нормали
точки выделяется бесконечносоответствующей
малый объемный
грани, т.е.элемент
они вызывают
деформацию
растяжения
элемента.
(параллелепипед со сторонами
dx, dy, dz),
по каждой
грани
которого действуют, в общем случае, три напряжения,
например, для грани, перпендикулярной оси x (площадка x) –
σx, xy, xz .
• Компоненты напряжений по трем перпендикулярным
граням элемента образуют систему напряжений,
y zy y σy
описываемую так называемым
y
z
xy x
• тензором напряжений:
σz
x yx zx
T xy y zy
yz
z
xz
z
xz
xz
zx
σx
x
Здесь первый столбец представляет компоненты напряжений
на площадках, нормальных к оси x, второй и третий – к оси y и
z соответственно. Первый индекс указывает площадку
(“место”) действия, второй – направление. Для нормальных
напряжений индексы совпадают и один индекс опускается.

3.

Напомним, что опорные реакции конструкции включаются
в число внешних сил. Для определения этих реакций в
статически неопределимых системах уравнений равновесия
недостаточно и следует дополнительно рассматривать
перемещения, связанные с внутренними усилиями и
напряжениями, а также физические соотношения упругости.
Таким образом, в целом связь внешних сил, внутренних
усилий и напряжений такова:
Внешние силы
Внутренние
усилия
Уравнения равновесия
Q x X i оставл.части 0;
Q y Yi
оставл.части
N Zi
оставл.части
0;
0;
Напряжения
Интегральные соотношения
M x M xi оставл.части 0; N dA
M y M уi
M z M zi
оставл.части
оставл.части
A
0; QY ZY dA
0.
A
M X ydA
A
T dA
A
Q X ZX dA
A
M Y xdA
A

4. Деформации и перемещения.

Перемещения – переход точек тела в новое положение
вследствие изменения формы и размеров тела под
действием нагрузки.
Полное перемещение точки в пространстве раскладывается
на компоненты u, v и w, параллельные осям x, y и z,
соответственно.
Перемещения рассматриваемой точки зависит от
деформации всех нагруженных областей тела и
включают в себя перемещения как жесткого целого
ненагруженных областей.
Таким образом, перемещения не могут
характеризовать степень деформирования в
окрестности рассматриваемой точки.
■
Деформация в точке – мера деформирования материала
в ее окрестности.

5.

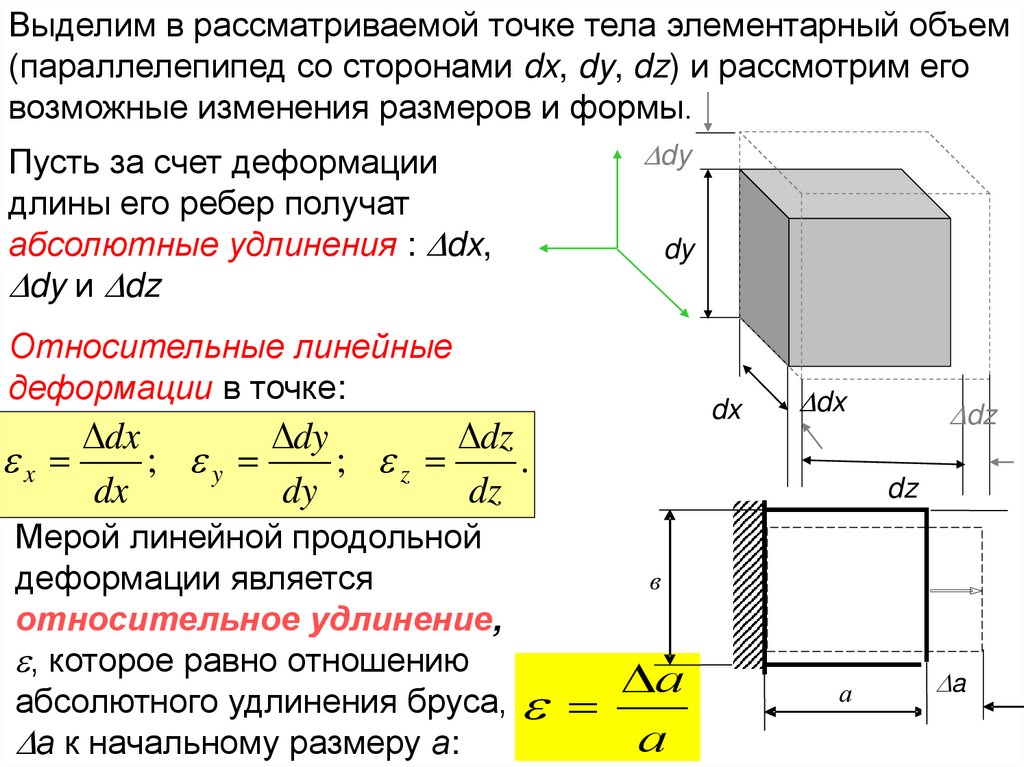
Выделим в рассматриваемой точке тела элементарный объем
(параллелепипед со сторонами dx, dy, dz) и рассмотрим его
возможные изменения размеров и формы.
Пусть за счет деформации
длины его ребер получат
абсолютные удлинения : dx,
dy и dz
dy
dy
Относительные линейные
деформации в точке:
dx
dy
dz
x
; y
; z
.
dx
dy
dz
Мерой линейной продольной
в
деформации является
относительное удлинение,
, которое равно отношению
а
абсолютного удлинения бруса,
а
а к начальному размеру а:
dx
dx
dz
dz
а
a

6.

Угловыми называются деформации, при которых
изменяются углы между ребрами бруса за счет сдвига одной
плоскости элемента относительно другой.
s
а
Величина перемещения любой
точки в плоскости сдвига s,
F
называется абсолютным
g
сдвигом.
а
Мерой угловой деформации
является относительный сдвиг,
g, который равен отношению
абсолютного сдвига s к расстоянию
x
s
между плоскостями сдвига а:
y
g
Если опять вернуться к
а
g
xy
dy
параллелепипеду, то в плоскости
xy могут возникать малые
изменения первоначально
dx
x
x
прямых углов
tgg xy g xy .
параллелепипеда:
dy

7.

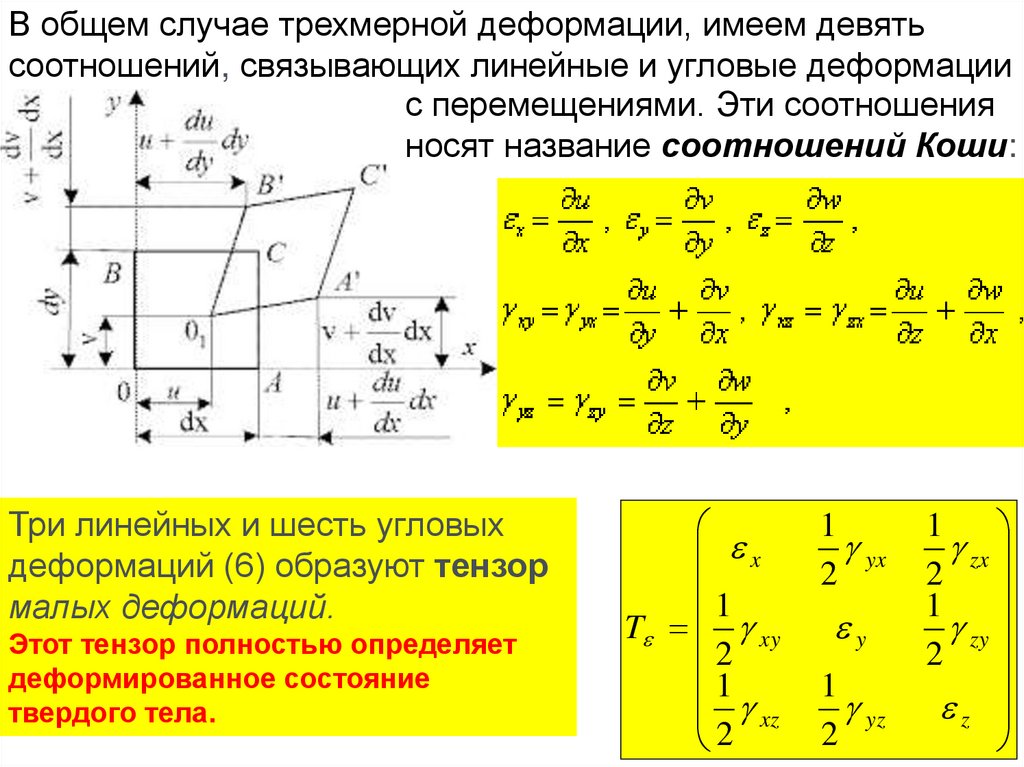
В общем случае трехмерной деформации, имеем девять
соотношений, связывающих линейные и угловые деформации
с перемещениями. Эти соотношения
носят название соотношений Коши:
Три линейных и шесть угловых
деформаций (6) образуют тензор
малых деформаций.
Этот тензор полностью определяет
деформированное состояние
твердого тела.
x
1
T g xy
2
1
g xz
2
1
g yx
2
y
1
g yz
2
1
g zx
2
1
g zy
2
z

8.

Все относительные деформации весьма малы и имеют для
реальных материалов порядок ≈10-4-10-3.
Таким образом, совокупность относительных линейных и
угловых деформаций определяют деформированное
состояние в точке и образуют тензор деформаций,
подобный тензору напряжений:
x yx zx
T xy y zy
yz
z
xz
x
1
T g xy
2
1
g xz
2
1
g yx
2
y
1
g yz
2
1
g zx
2
1
g zy
2
z
Половинные углы сдвига используются в целях получения
аналогичных формул преобразования с тензором напряжений.

9.

В зависимости от того, какие из компонент относительных
деформаций имеют нулевое значение в рассматриваемой
области или для всего тела различают следующие простые
виды деформаций:
1.Линейная деформация – εz ≠ 0, углы сдвига равны нулю,
остальными линейными относительными деформациями
пренебрегается
(характеризуется абсолютным и относительным удлинением).
2.Плоская деформация – εz ≠ 0, εx ≠ 0 или εy ≠ 0, остальные
относительные деформации равны нулю (характеризуется
абсолютным и относительным
сужением площади поперечного
сечения). Эти виды деформаций
обычно реализуются при
растяжении-сжатии.

10.

3.Объемная деформация – εz ≠ 0, εx ≠ 0, εy ≠ 0, углы сдвига
равны нулю(характеризуется абсолютным и относительным
изменением объема).
4.Чистый сдвиг – линейные относительные деформации
равны нулю, углы сдвига не равны нулю (характеризуется
изменением формы, изменение объема не происходит). Это
вид деформации также возникает при кручении.
В соответствии с видом деформации
вначале последовательно изучают
такие простейшие напряженнодеформированные состояния как
растяжение-сжатие, чистый сдвиг и
кручение, чистый изгиб. Далее
изучаются более сложные –
поперечный изгиб, сложное
сопротивление,продольный изгиб.

11. Температурные деформации

Изменения температуры вызывают расширение или
сокращение конструкционных материалов, в результате чего в них возникают
температурные деформации и температурные напряжения.
Когда этот брусок нагревается, каждый элемент материала подвергается
температурным деформациям по всем направлениям, и, соответственно, размеры
бруска увеличиваются также во всех направлениях. Если взять угол А за точку
отсчета и дать стороне АВ возможность сохранять свое исходное направление, то
брусок примет форму, которая показана штриховыми линиями. Для большинства
конструкционных материалов температурная деформация εT является
пропорциональной изменению температуры ΔT, то есть
εT = α·ΔT,
(1)
где α – свойство материала, которое
называется коэффициентом
температурного расширения. Согласно
принятому в мире «знаковому соглашению»
температурное расширение считается
положительным, а температурное
сокращение – отрицательным.
Δlt = α·ΔTl

12. Центральное растяжение-сжатие

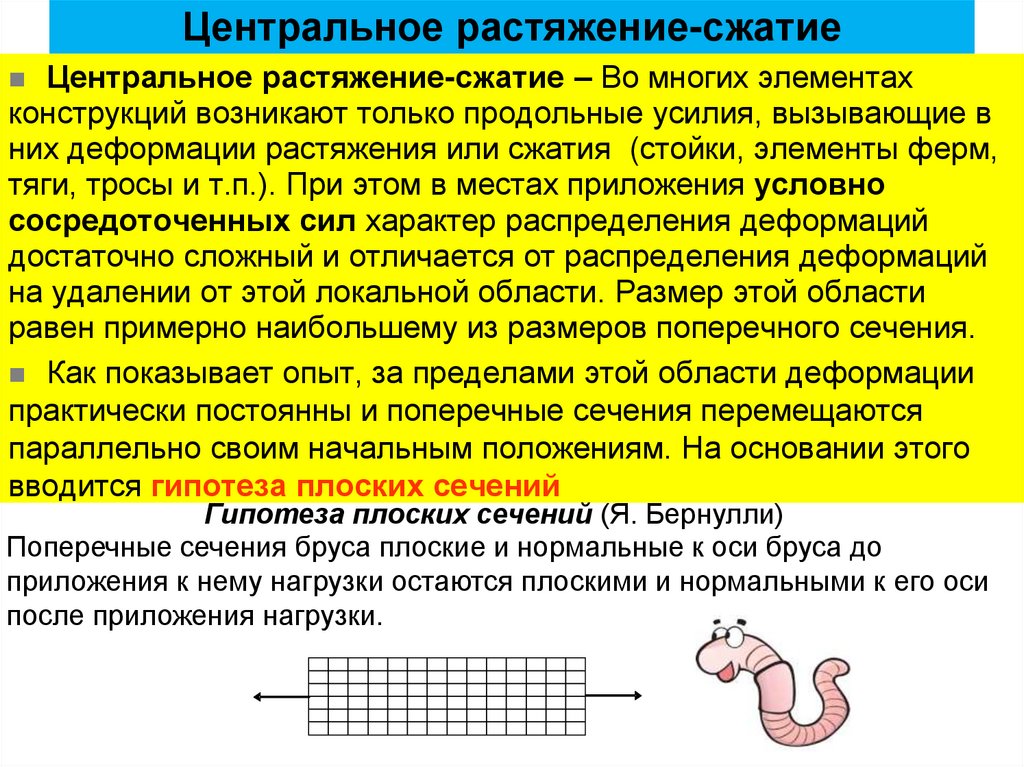
Центральное растяжение-сжатие – Во многих элементах
конструкций возникают только продольные усилия, вызывающие в
них деформации растяжения или сжатия (стойки, элементы ферм,
тяги, тросы и т.п.). При этом в местах приложения условно
сосредоточенных сил характер распределения деформаций
достаточно сложный и отличается от распределения деформаций
на удалении от этой локальной области. Размер этой области
равен примерно наибольшему из размеров поперечного сечения.
Как показывает опыт, за пределами этой области деформации
практически постоянны и поперечные сечения перемещаются
параллельно своим начальным положениям. На основании этого
вводится гипотеза плоских сечений
Гипотеза плоских сечений (Я. Бернулли)
Поперечные сечения бруса плоские и нормальные к оси бруса до
приложения к нему нагрузки остаются плоскими и нормальными к его оси
после приложения нагрузки.

13.

Принцип Сен-Венана - Если совокупность некоторых
сил, приложенных к небольшой части поверхности тела,
заменить статически эквивалентной системой других сил,
то такая замена не вызовет существенных изменений в
условиях нагружения частей тела, достаточно удаленных
от мест приложения исходной системы сил.
Напряжения и деформации – Как было ранее сказано,
задача определения напряжений всегда является
статически неопределимой.
Такие задачи решаются последовательным рассмотрением
статической, геометрической и физической сторон.
В данном случае имеем статическое уравнение,
связывающее внутреннее усилие – продольную силу с
напряжением:
N z dA;
A
Для вычисления интеграла необходимо
знать закон изменения напряжений по
сечению.

14.

Деформация, при которой в поперечном сечении бруса возникает один силовой фактор - продольная сила N, называется
растяжением (сжатием).
Продольной силой N называется равнодействующая
внутренних сил, распределенных по площади
N dA
A
поперечного сечения (нормальных напряжений):
При равномерном распределении нормальных напряжений :
N A
Правило знаков: Продольная сила считается положительной, если она
вызывает растяжение, т.е. направлена от сечения (в сторону внешней
нормали), и отрицательной, если она вызывает сжатие, т.е. направлено к
Сущность метода сечений заключается
сечению.
в том, что величина продольной
силы в сечении стержня равна
y
сумме всех внешних продольных
II
I
сил приложенных по одну из сторон
F5 от выбранного сечения.
F2
F4
F3
F1
A
x
C
B
I
E
D
II
N1-1= -F1-F2= -10-15= -25 кН,
K
z F1=10 кН, F2=15 кН, F3=55 кН, F4=30 кН;
Определим продольные силы в
сечениях I-I и II-II.
N11-11= -F1-F2+F3= -10-15+55=30 кН.

15. Построение эпюры продольных сил

Характерными называются сечения стержня где: 1) приложены внешние
продольные силы; 2) происходит ступенчатое, или начинается участок
постепенного изменения площади поперечного сечения бруса.
Эпюрой продольных сил называется график изменения продольной
силы по длине стержня (бруса).
y
Дано: F1=10 кН, F2=15 кН, F3=55 кН,
F4=30 кН.
F2
F1
A
F3
B
C
F5
F4
D
E
K
x
z
Построить эпюру продольных сил
Участок АВ NАВ=-F1=-10 кН.
Участок ВС NВС= -F1-F2= -10-15= -25 кН.
Эпюра N , кН
Участок CD NCD= -F1-F2= -10-15= -25 кН.
Участок DE NDE= -F1-F2+F3=-10-15+55=30 кН
30
15
10
25
Участок ЕК NEK= -F1-F2+F3-F4=
= -10-15+55-15=15 кН.

16. Построение эпюры продольных сил

Правила контроля эпюры продольных сил
Основные правила контроля правильности
построения эпюры продольных сил можно
сформулировать так:
1. В сечении, где приложена сосредоточенная сила F,
эпюра продольных сил делает скачок на величину
этой силы и с ее знаком.
2. Изменение площади поперечного сечения стержня
влияния на эпюру продольных сил не оказывает,
независимо от характера этого изменения
(ступенчатое или постепенное).
3. На участке, где приложена равномерно
распределенная нагрузка эпюра продольных сил
имеет вид прямой наклонной линии.

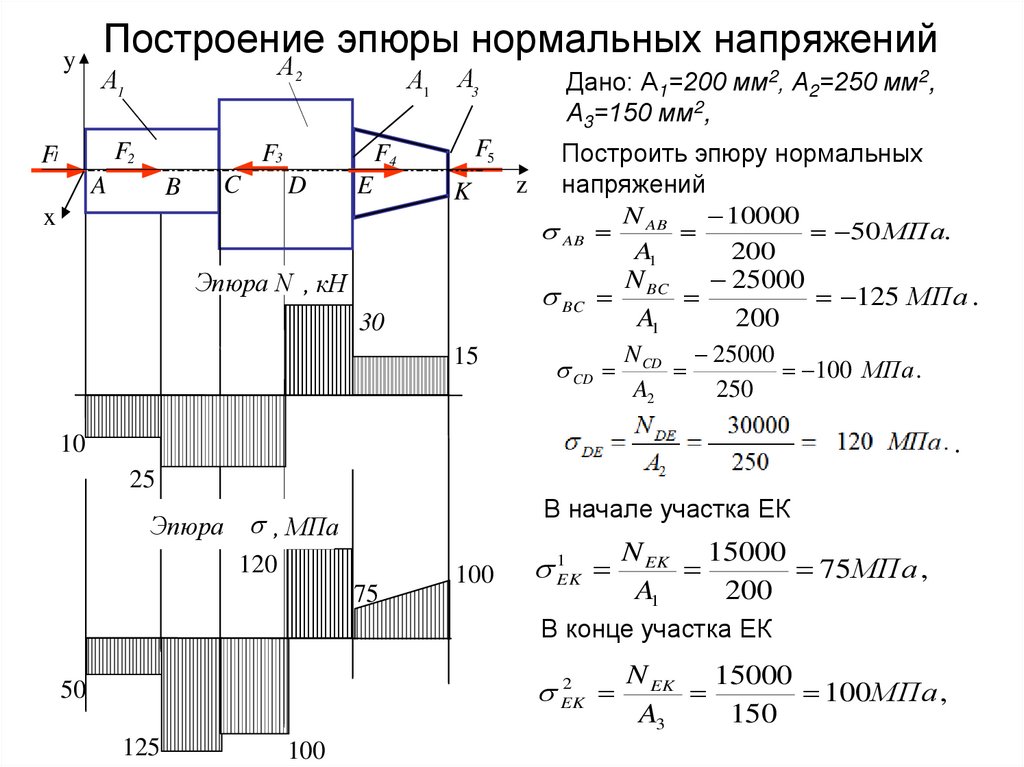
17. Построение эпюры нормальных напряжений

y
Построение эпюры нормальных напряжений
А2
А1
F2
F1
А1
F3
A
B
C
А3
Дано: А1=200 мм2, А2=250 мм2,
А3=150 мм2,
F5
Построить эпюру нормальных
z напряжений
N
10000
AB AB
50 МПа.
A1
200
N
25000
BC BC
125 МПа .
A1
200
N
25000
CD CD
100 МПа .
A2
250
F4
D
E
K
x
Эпюра N , кН
30
15
DE
10
25
N DE 30000
120 МПа .
A2
250
В начале участка ЕК
Эпюра , МПа
120
75
100
1EK
N EK 15000
75МПа ,
A1
200
В конце участка ЕК
2
EK
50
125
100
N EK 15000
100 МПа ,
A3
150

18. Деформация растяжения

Правила контроля эпюры нормальных напряжений
Основные правила контроля правильности построения эпюры
нормальных напряжений можно сформулировать так:
1. На участке или в сечении стержня, где происходит
изменение площади поперечного сечения, нормальные
напряжения изменяются обратно пропорционально
изменению площади, если площадь изменяется
ступенчато, то на эпюре наблюдается скачок, если
площадь изменяется постепенно, то эпюра имеет вид
прямой наклонной линии
2. В сечении, где приложена сосредоточенная сила эпюра
нормальных напряжений, делает скачок на величину
пропорциональную силе и с ее знаком.
3. На участке, где приложена равномерно распределенная
нагрузка эпюра нормальных напряжений имеет вид
прямой наклонной линии

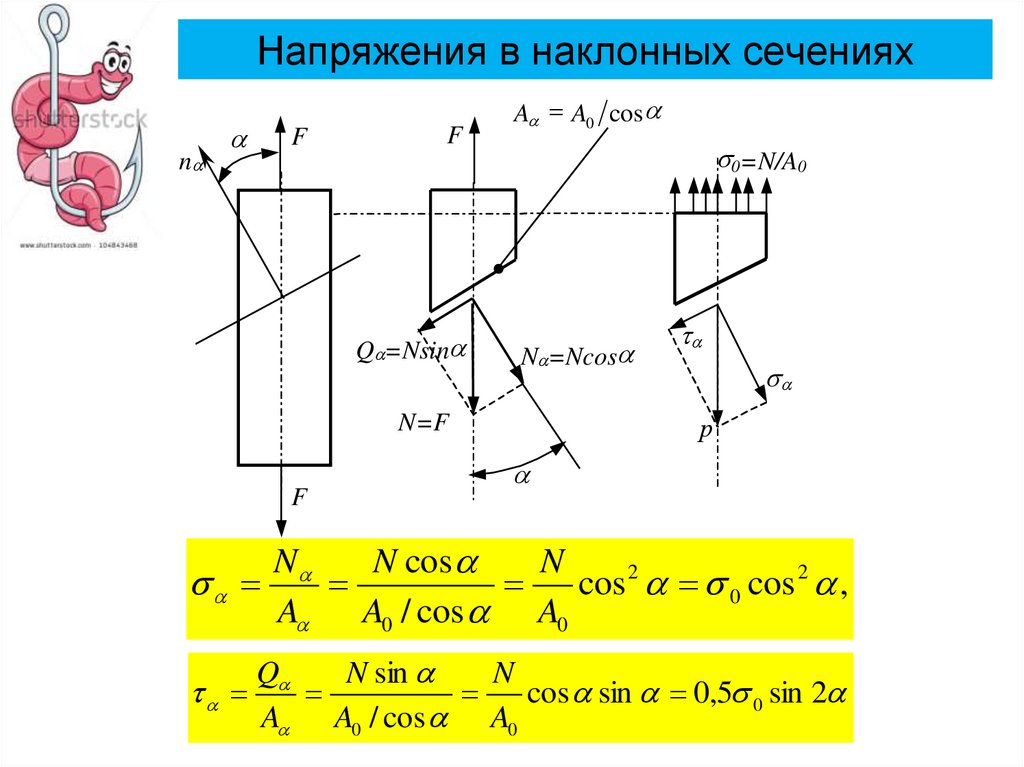
19. Напряжения в наклонных сечениях

n
F
F
Q =Nsin
A A0 cos
0=N/A0
N =Ncos
N=F
F
р
N
N cos
N
cos 2 0 cos 2 ,
A
A0 / cos A0
Q
N sin
N
cos sin 0,5 0 sin 2
A A0 / cos A0

20. Напряжения в наклонных сечениях

Знак нормального напряжения определяется знаком
продольной силы, то есть растягивающее напряжение
положительно, сжимающее – отрицательно.
Касательное напряжение считается положительным,
если изображающий его вектор стремится вращать тело
относительно любой точки, лежащей на внешней нормали
к сечению против часовой стрелки.
N
N cos
N
cos 2 0 cos 2 ,
A
A0 / cos A0
Q
N sin
N
cos sin 0,5 0 sin 2
A A0 / cos A0

21.

Анализ полученных соотношений показывает:
1. При = 0 (наклонная площадка совпадает с
поперечным сечением):
; 0.
z
Касательные напряжения отсутствуют, а нормальные
напряжения максимальны.
2. При = 45о касательные напряжения максимальны и
равны нормальным.
2
1
, cos 2 450 ;
2
2
sin 2 450 sin 900 1.
cos 450
3. При = 90о (продольная площадка) нормальные и
касательные напряжения обращаются в ноль (продольные
волокна не давят друг на друга и не сдвигаются).
4. На двух взаимно перпендикулярных площадках
касательные напряжения равны по абсолютной величине.

22. Деформации и перемещения

lк
l0
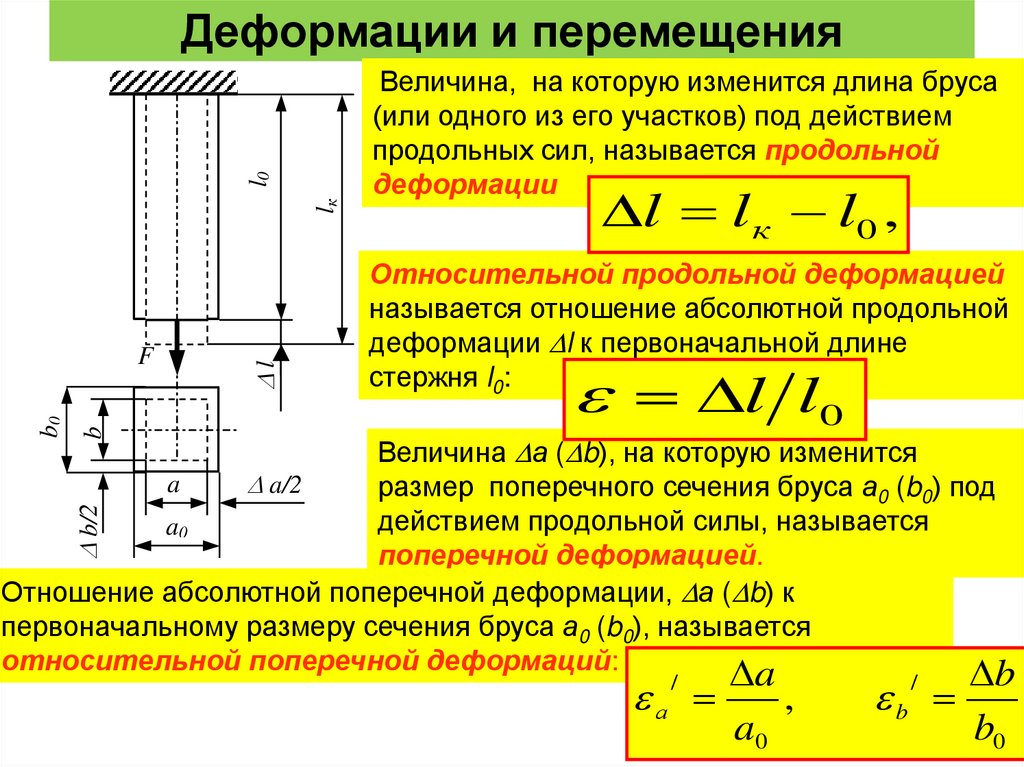
Деформации и перемещения
Величина, на которую изменится длина бруса
(или одного из его участков) под действием
продольных сил, называется продольной
деформации
l lк l0 ,
b
l l
b/2
b0
l
Относительной продольной деформацией
называется отношение абсолютной продольной
деформации l к первоначальной длине
F
стержня l0:
0
Величина а ( b), на которую изменится
a
a/2
размер поперечного сечения бруса а0 (b0) под
действием продольной силы, называется
a0
поперечной деформацией.
Отношение абсолютной поперечной деформации, а ( b) к
первоначальному размеру сечения бруса а0 (b0), называется
относительной поперечной деформаций:
a
а
,
a0
/
b
b
b0
/

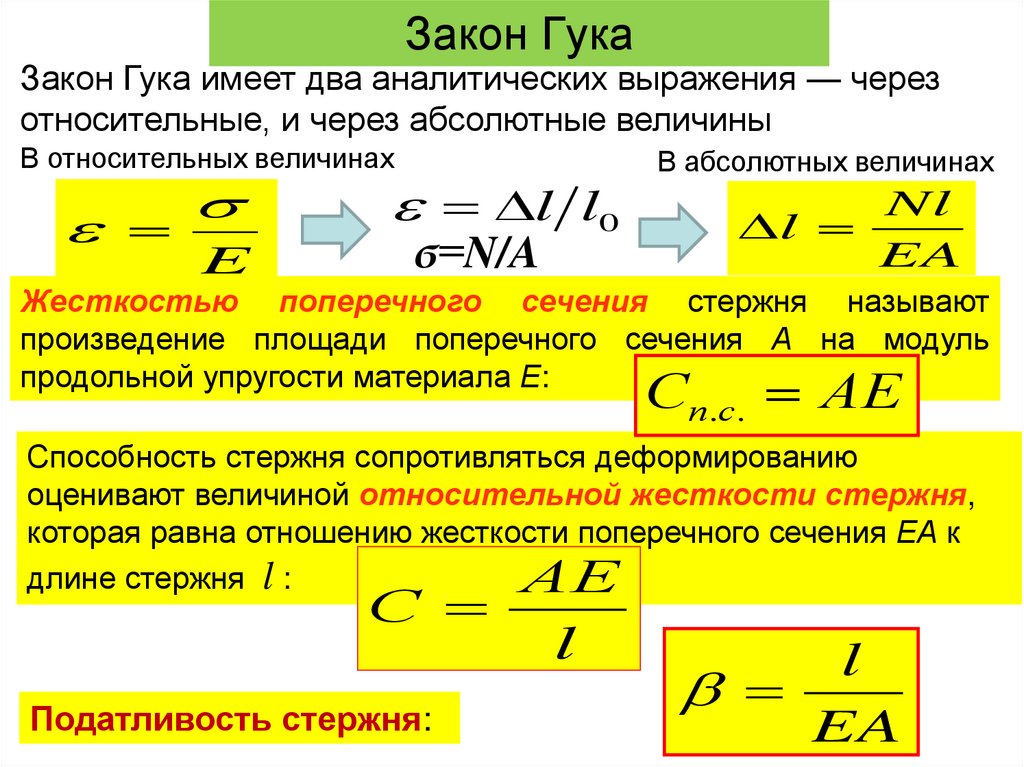
23. Закон Гука

Закон Гука имеет два аналитических выражения — через
относительные, и через абсолютные величины
В относительных величинах
E
l l0
ϭ=N/A
В абсолютных величинах
Nl
l
EA
Жесткостью поперечного сечения стержня называют
произведение площади поперечного сечения А на модуль
продольной упругости материала Е:
Сп.с. АЕ
Способность стержня сопротивляться деформированию
оценивают величиной относительной жесткости стержня,
которая равна отношению жесткости поперечного сечения ЕА к
длине стержня l :
АЕ
С
Податливость стержня:
l
l
EA

24.

N
σ
+
+
dz
l
z
Q=Azg
l
l
0
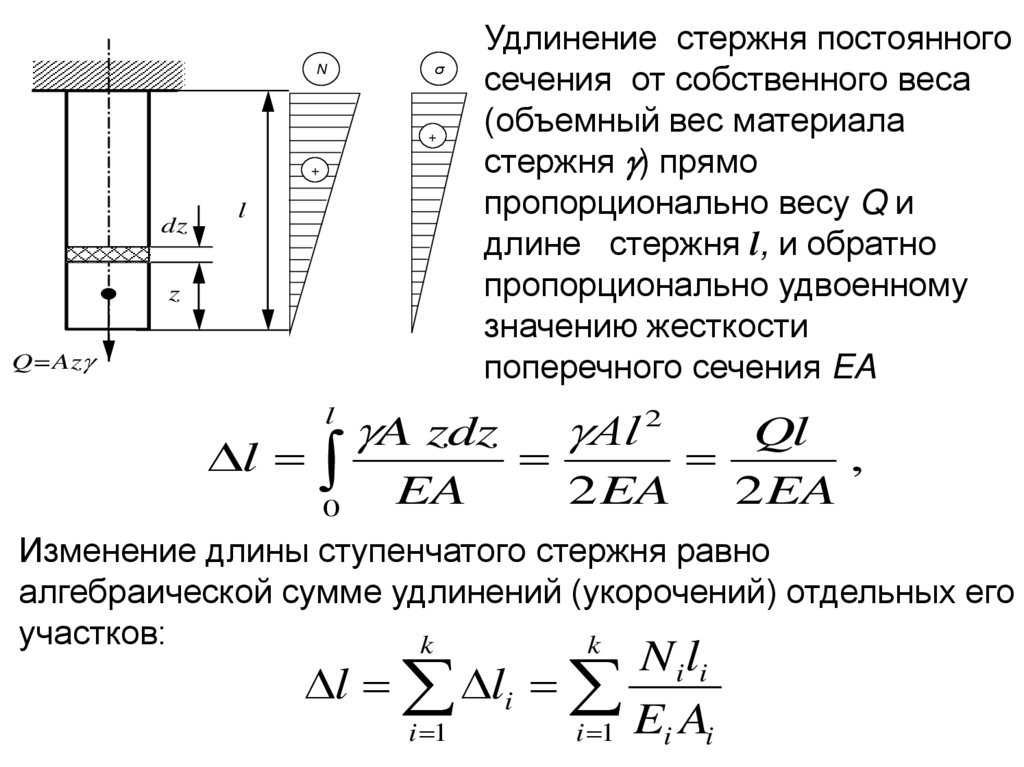
Удлинение стержня постоянного
сечения от собственного веса
(объемный вес материала
стержня g) прямо
пропорционально весу Q и
длине стержня l, и обратно
пропорционально удвоенному
значению жесткости
поперечного сечения EA
gA zdz
EA
gАl 2
Ql
,
2 EA
2 EA
Изменение длины ступенчатого стержня равно
алгебраической сумме удлинений (укорочений) отдельных его
участков:
k
k
N i li
l li
i 1
i 1 Ei Ai

25.

а
a/2
0
b
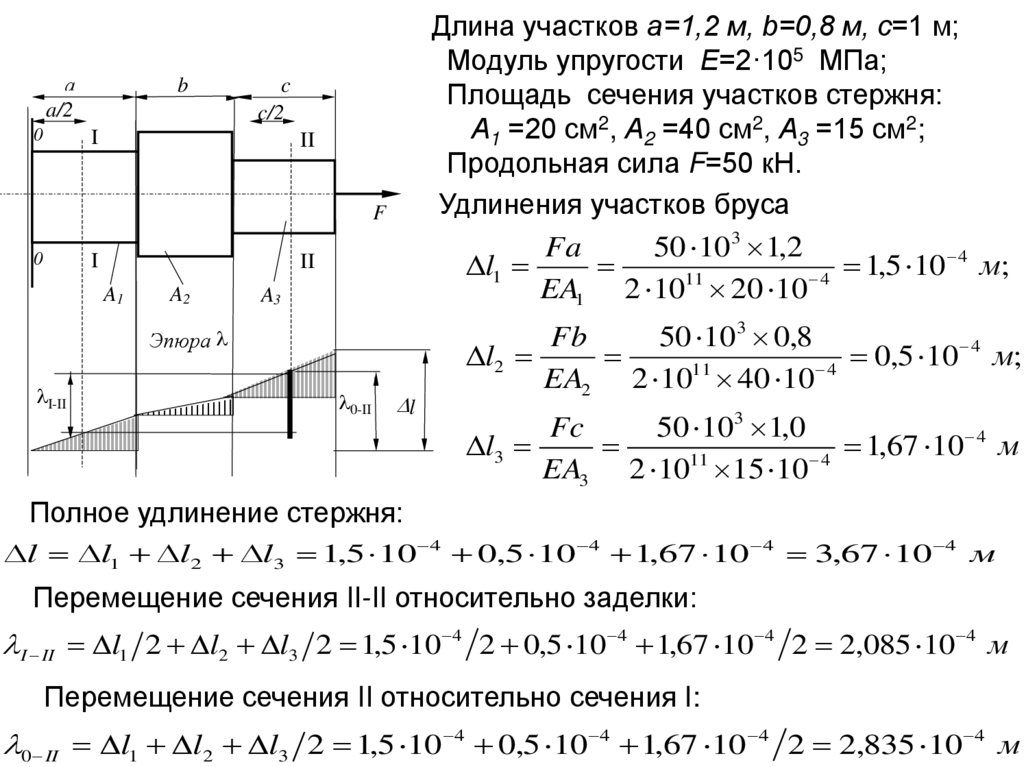
Длина участков а=1,2 м, b=0,8 м, c=1 м;
Модуль упругости Е=2·105 МПа;
Площадь сечения участков стержня:
А1 =20 см2, А2 =40 см2, А3 =15 см2;
Продольная сила F=50 кН.
Удлинения участков бруса
Fa
50 103 1,2
4
l1
1
,
5
10
м;
11
4
EA1 2 10 20 10
c
c/2
I
II
F
0
I
II
A1
A2
A3
Эпюра l
lI-II
l0-II
l
Fb
50 103 0,8
4
l2
0
,
5
10
м;
11
4
EA2 2 10 40 10
Fc
50 103 1,0
4
l3
1
,
67
10
м
11
4
EA3 2 10 15 10
Полное удлинение стержня:
l l1 l2 l3 1,5 10 4 0,5 10 4 1,67 10 4 3,67 10 4 м
Перемещение сечения II-II относительно заделки:
lI II l1 2 l2 l3 2 1,5 10 4 2 0,5 10 4 1,67 10 4 2 2,085 10 4 м
Перемещение сечения II относительно сечения I:
l0 II l1 l2 l3 2 1,5 10 4 0,5 10 4 1,67 10 4 2 2,835 10 4 м

26. Коэффициент Пуассона

Отношение относительной поперечной деформации к
относительной продольной деформации взятое по модулю,
называется коэффициентом Пуассона:
/
попер прод
Коэффициент Пуассона принимает значения в пределах от 0 до 0,5 и определяется экспериментально. Меньшее значение коэффициента имеют бетон – 0,16…
0,18, стекло – 0,25, большие значения каучук – 0,48, свинец – 0,42, целлулоид –
0,38. У большинства материалов используемых в машиностроении =0,24…0,36.
Коэффициентом изменения объёма называется безразмерная
величина представляющая собой отношение величины, на которую
изменяется объём бруса при деформации V=Vк-V0 к его
первоначальному объёму V0
/
/
/
/
kV a b 2 1 2 1 2 .
Коэффициент изменения объема принимает следующие значения:
при сжатии объём бруса уменьшается и kV<0, при растяжении объём
увеличивается и kV>0. Для материалов с коэффициентом Пуассона
0,5 изменение объёма не происходит и kV 0

27.

• По закону Гука, определяющему связь нормальных напряжений с
продольными деформациями:
Тогда
x y z
z
E
z
.
z
E
.
В общем случае нагружения по граням выделенного элемента возникают
нормальные и касательные напряжения. Последние, вызывая деформации сдвига,
не влияют на линейные деформации, поскольку не изменяют длин сторон
элемента. Используя принцип независимости действия сил, справедливый для
изотропного и линейно упругого материала, можно записать обобщенный закон
Гука, учитывающий одновременное действие нормальных напряжений по всем
граням элемента:
Обобщенный закон Гука:
1
x [ x ( y z )];
E
1
y [ y ( z x )];
E
1
z [ z ( x y )].
E

28. Механические характеристики материалов

Испытание материалов на растяжение – сжатие
При проектировании конструкций, машин и механизмов
необходимо знать прочностные и деформационные свойства
материалов. Их определяют экспериментально на специальных испытательных машинах. Из всех прочих свойств (твердость, сопротивляемость ударным нагрузкам, противодействие высоким или низким температурам и т.п.) основными
является сопротивление на растяжение и сжатие, дающие
наибольшую и важнейшую информацию о механических
свойствах металлов.
Испытание на растяжение – проводят на разрывных или
универсальных машинах, имеющих специальные захваты для
передачи усилия. Используются стандартные d
0
образцы специальной формы
(l0 – длина рабочей части,
l0
a0
l0/ d0 = 5 – короткие,
b0
l0/ d0 = 10 – длинные):
l

29. Механические характеристики материалов

При испытаниях на сжатие применяются
цилиндрические образцы с отношением высоты к
диаметру h/d = 1,5 – 3.
Образцы устанавливаются на опорную поверхность
с использованием смазки для ослабления влияния
сил трения.
Все машины снабжены устройством для
автоматической записи в определенном
масштабе диаграммы-графика зависимости
величины растягивающей силы от
удлинения образца.
Диаграммы растяжения пластичных и
хрупких материалов
Характерной
диаграммой пластичных материалов
является диаграмма растяжения
низкоуглеродистой
стали (< 0,25% С)

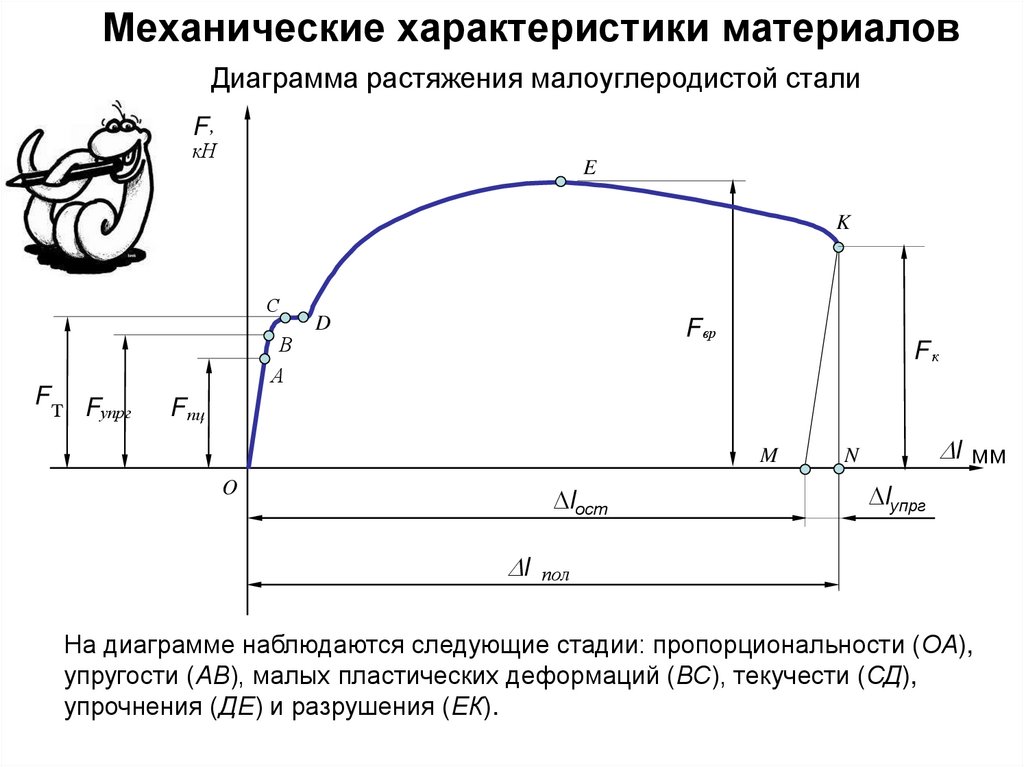
30. Механические характеристики материалов

Диаграмма растяжения малоуглеродистой стали
F,
кН
E
K
С
Fт F
упрг
В
А
D
F вр
Fк
F пц
M
O
lост
l мм
N
lупрг
l пол
На диаграмме наблюдаются следующие стадии: пропорциональности (ОА),
упругости (АВ), малых пластических деформаций (ВС), текучести (СД),
упрочнения (ДЕ) и разрушения (ЕК).

31. Механические характеристики материалов

Характеристики прочности
К характеристикам прочности относят: предел пропорциональности пц,
предел упругости упрг, предел текучести Т, временное сопротивление
разрыву вр (сжатию вс), предел прочности пч.
Пределом пропорциональности пц называется такое
максимальное напряжение, до которого наблюдается прямая
Fпц
зависимость между нагрузкой и деформацией:
пц
A0
Условным пределом пропорциональности 0,001 называется такое
наименьшее напряжение, при котором отклонение от линейной
зависимости между напряжением и деформацией достигают заданной
величины - 0,001 %.
Пределом упругости упр называется такое максимальное напряжение,
до которого в материале не возникает остаточных деформаций:
упр
Fупр
A0
Условным пределом упругости 0,05 называется такое наименьшее
напряжение, при котором в материале возникают остаточных деформаций
равные заданной величине - 0,05%.

32. Механические характеристики материалов

Характеристики прочности
Физическим пределом текучести Т называется такое мини-
мальное напряжение, при котором в образце возникают значительные остаточные деформации и они продолжают увеличиваться при
Fт
постоянном значении нагрузки:
т
A0
Условным пределом текучести 0,2 называется наибольшее напряжение, при котором остаточные деформации, возникающие в образце, не
превышают какой-то наперед заданной величины, обычно 0,2 %
Временным сопротивлением разрыву вр называется условное
наибольшее растягивающее напряжение, которое выдержит образец:
Fmax
вр
A0
Пределом прочности пч называется максимальное напряжение,
которое может выдержать образец без явных признаков разрушения.
Величина предела прочности равна временному сопротивлению сжатию
вс (разрыву вр ).

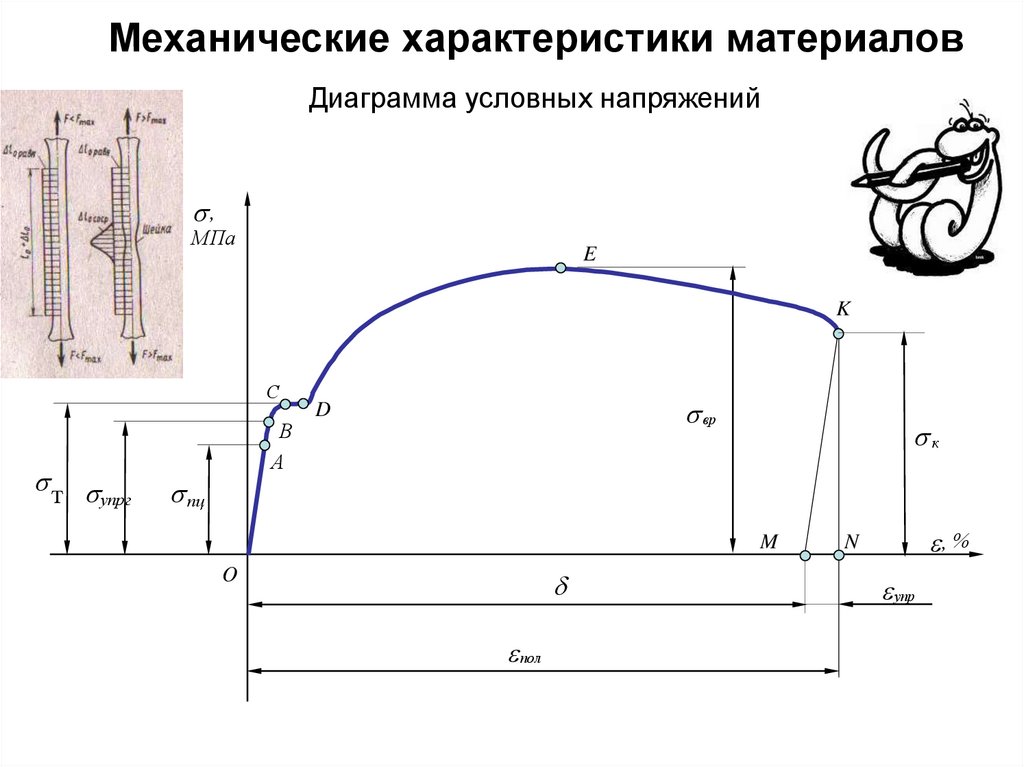
33.

Механические характеристики материалов
Диаграмма условных напряжений
,
МПа
E
K
С
т
упрг
В
А
вр
D
к
пц
M
O
d
пол
, %
N
упр

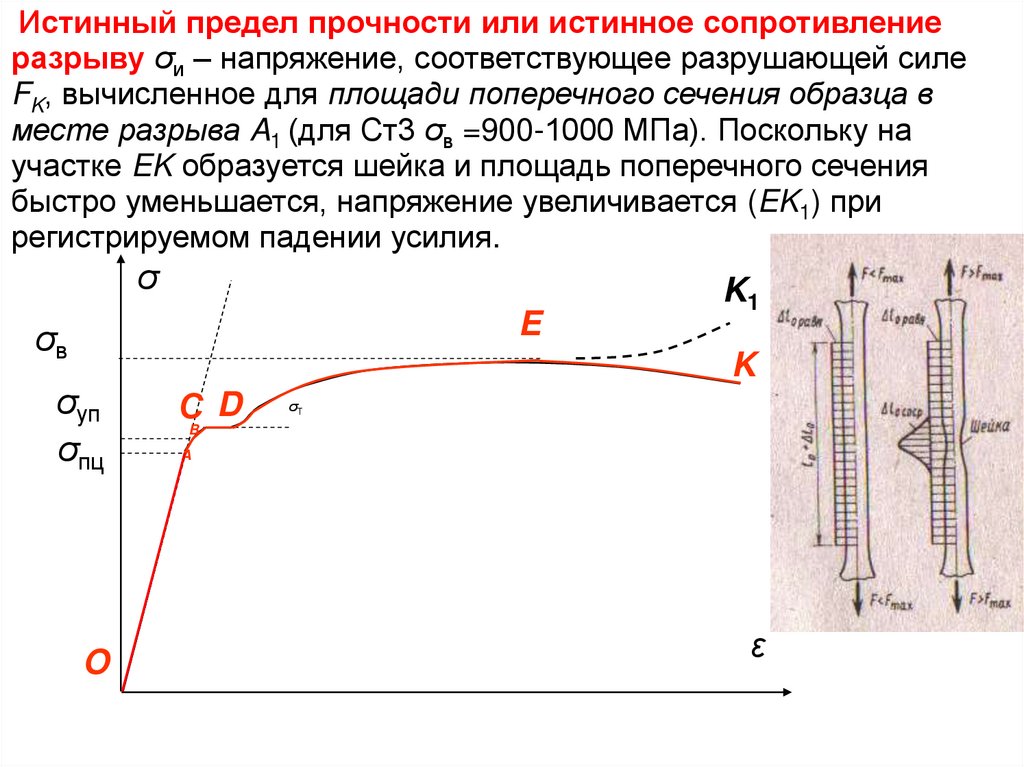
34.

Истинный предел прочности или истинное сопротивление
разрыву σи – напряжение, соответствующее разрушающей силе
FK, вычисленное для площади поперечного сечения образца в
месте разрыва A1 (для Ст3 σв =900-1000 МПа). Поскольку на
участке EK образуется шейка и площадь поперечного сечения
быстро уменьшается, напряжение увеличивается (EK1) при
регистрируемом падении усилия.
σ
E
σв
σуп
σпц
O
K1
K
СB D
σТ
A
ε

35. Механические характеристики материалов

Характеристики пластичности
К характеристикам пластичности относят относительное остаточное
удлинение d и относительное остаточное сужение площади поперечного
сечения .
Относительным остаточным удлинением d называется отношение остаточной деформации lост образца к его первоначальной длине l0
выраженное в процентах:
l
l l
d ост 100% к
l0
0
l0
100%
Относительным остаточным сужением называется отношение
изменения площади поперечного сечения образца в месте разрыва к
первоначальной площади А0 поперечного сечения выраженное в
процентах:
A0 Aш
A0
100%
Пластические свойства материалов оцениваются величиной
относительного остаточного удлинения d. Для оценки приняты
следующие условия:
•если d<5 % материал считается хрупким;
•если 5 % <d < 10 % - хрупко—пластичным;
•если d > 10 % - пластичным.

36. Допускаемые напряжения

Опасным называется напряжениеσ0 при котором конструкция
становится не работоспособной.
Для конструкций из пластичных материалов основной
причиной потери работоспособности являются
большие пластические деформации и в этом случае
опасное напряжение равно физическому пределу текучести:
ϭ0 = ϭт.
Для пластичных не имеющих физического предела
текучести, опасное напряжение приравнивается к
условному пределу текучести:
ϭ 0 = ϭ0,2.
Для конструкций из хрупких материалов основной
причиной потери работоспособности является
разрушение, которое происходит, как правило, без видимых
остаточных деформаций. И в качестве опасного напряжения
принимают предел прочности ϭпч или временное
сопротивление разрыву ϭвр.

37.

Запас прочности
Под коэффициентом запаса прочности понимают
величину, указывающую во сколько раз необходимо
уменьшить опасное напряжение ϭ0 , чтобы прочность
конструкции или детали, в заданных условиях
эксплуатации, была гарантирована, а максимальные
напряжения, в любом случае, не превышали предела
пропорциональности ϭпц .
Величину коэффициента запаса прочности для
пластичных материалов рекомендуется выбирать из
интервала
SТ = 1,25-2,5.
Коэффициент запаса прочности для хрупких материалов,
изменяется в пределах
Sвр = 2,4 – 5,0.

38. Допускаемые напряжения

Допускаемыми называются наибольшие напряжения,
которые можно допустить в рассчитываемой конструкции
из условий ее безопасной, надежной и долговечной
работы.
т
sт
0 , 2
S
sт
в р
sв р
для пластичных материалов
для пластичных материалов не
имеющих физического предела
текучести
для хрупких материалов

39. Расчеты на прочность при растяжении

Расчётными называются напряжения вычисленные по теоретическим
или экспериментальным формулам для конкретной конструкции с учетом
величины приложенных к ней внешних нагрузок, размеров и формы ее
элементов.
F
A
Условие прочности формулируется так нормальные расчетные
напряжения в любом сечении растянутого (сжатого) стержня не
должны превышать допускаемого значения:
Из условия прочности при растяжении (сжатии) вытекают
следующие задачи:
1. Задача проверочного
расчета
F
A
2. Задача проектного
расчета.
3. Задача определения максимальной допускаемой
грузоподъемности
A
F
F A