Кинематика твердого тела

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция 4
Кинематика твердого тела
§4.1. Кинематика простейших движений твердого тела.
Вспомним, что модель твердого тела используется в ТМ в
том случае, когда при описании движения исследуемого
объекта требуется рассмотреть не только его
поступательное движение, но и вращение как целого.
Твердое тело в процессе движения не деформируется и
поэтому расстояние между его точками остаются
неизменными в любой момент.

3.

§4.1.1. Простейшие движения твердого тела.
Рассмотрим простейшие движения твердого тела. К ним
относятся:
1. Поступательное движение
2. Вращение вокруг неподвижной оси.
3. Плоское или плоскопараллельное движение – все
точки тела движутся в плоскостях, параллельных
базовой плоскости.
4. Движение твердого тела вокруг неподвижной точки
или сферическое движение: все точки движутся по
поверхностям сфер, центры которых находятся в
неподвижной точке.
5. Произвольное движение твердого тела

4.

§4.2. Поступательное движение твердого тела.
Дадим определения:
Число кинематических независимых движений s,
которое может совершить твердое тело как целое,
называется числом его степеней свободы (в ТММ подвижностью твердого тела).
Полюсом называется точка твердого тела, движение
которой задано.
При поступательном движении все точки твердого тела
движутся по траекториям со скоростями и ускорениями
равными скорости полюса.

5.

Vi V p , ai a p , Трi Tp p i
Поступательные движения твердого тела имеет 3-и степени
свободы (S=3=1x + 1y +1z ) и полностью моделируется
движением ее полюса. Поэтому, кинематика поступательного
движения есть кинематика точки. Закон такого движения
тела задается уравнениями движения полюса:
x p x p(t), yp y p(t), zp z p(t)
(24)

6.

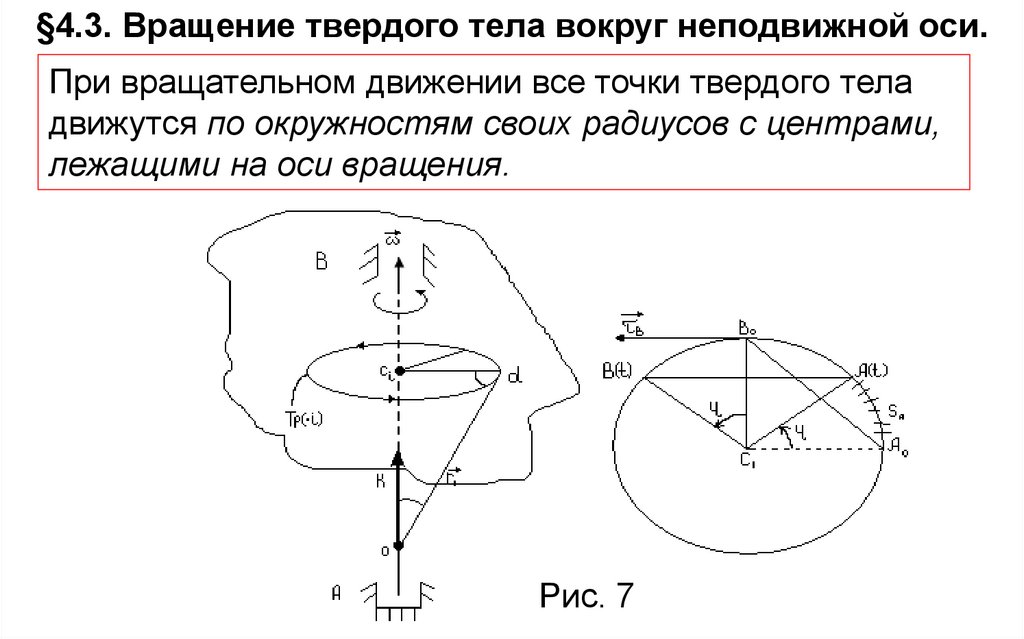
§4.3. Вращение твердого тела вокруг неподвижной оси.
При вращательном движении все точки твердого тела
движутся по окружностям своих радиусов с центрами,
лежащими на оси вращения.
Рис. 7

7.

Так как расстояния между точками в модели твердого тела
неизменны в процессе движения, то это движение имеет
всего1-у степень свободы (S=1) и задается законом
вращения
t
(25)

8.

§4.3.1.Угловые скорость и ускорение как кинематические
меры вращения твердого тела как целого.
Из физических основ механики следует, что
Угловая скорость тела как физическая величина
есть векторная кинематическая мера,
определяющая быстроту вращения тела как целого
в пространстве, численно равная d
(26)
dt
Угловое ускорение тела как физическая величина
есть вторая векторная кинематическая мера,
определяющая быстроту изменения угловой
скорости тела и численно равная d
(27)
dt

9.

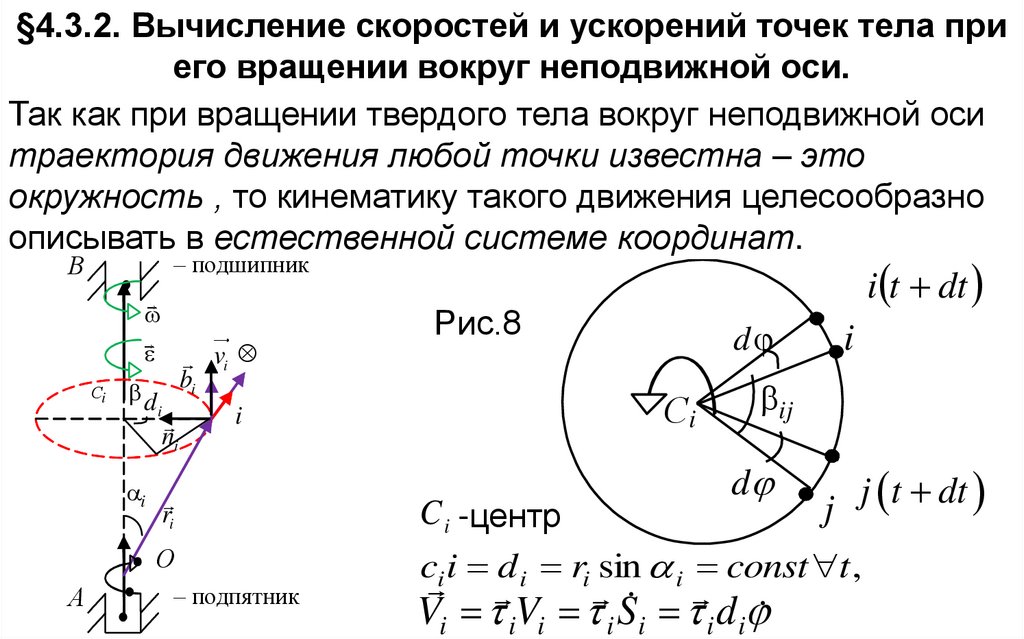
§4.3.2. Вычисление скоростей и ускорений точек тела при
его вращении вокруг неподвижной оси.
Так как при вращении твердого тела вокруг неподвижной оси
траектория движения любой точки известна – это
окружность , то кинематику такого движения целесообразно
описывать в естественной системе координат.
vi
b
d i
i
i
ni
Сi
i
А
i t dt
– подшипник
В
Рис.8
d
Сi
i
ij
d
j j t dt
ri
C i -центр
О
c i i d i ri sin i const t ,
– подпятник
Vi iVi i Si i di

10.

2
V
i
вр о.с.
ai iVi ni
ai ai
di
в р
ai ai
(28)
a in a iо .с .
вр - вращательное ускорение; a о.с. - осестремительное
ai
i
(центростремительное) ускорение.
Анализ выражений (28) показывает, что их можно представить
как векторные произведения, если ввести в этом случае
понятия угловой скорости и углового ускорения как (26), (27).
Тогда
Vi ri
ai [ ri ] [ Vi ]
(29)
(30)

11.

Выражения (29) называют формулой Эйлера, а (30) формулой Ривальса.
Вычислим ускорение точки непосредственно по определению
(16) и (29). Тогда
dri
dVi d
ai
[ ri ] [ ri ] [ ] [ ri ] [ Vi ]
dt dt
dt
(31)
что тождественно (30). Введя общепринятые в России
обозначения
вр
ос
ai [ Vi ] [ [ ri ]], ai ai [ ri ]
получим, что
вр ос
ai ai ai
(32)

12.

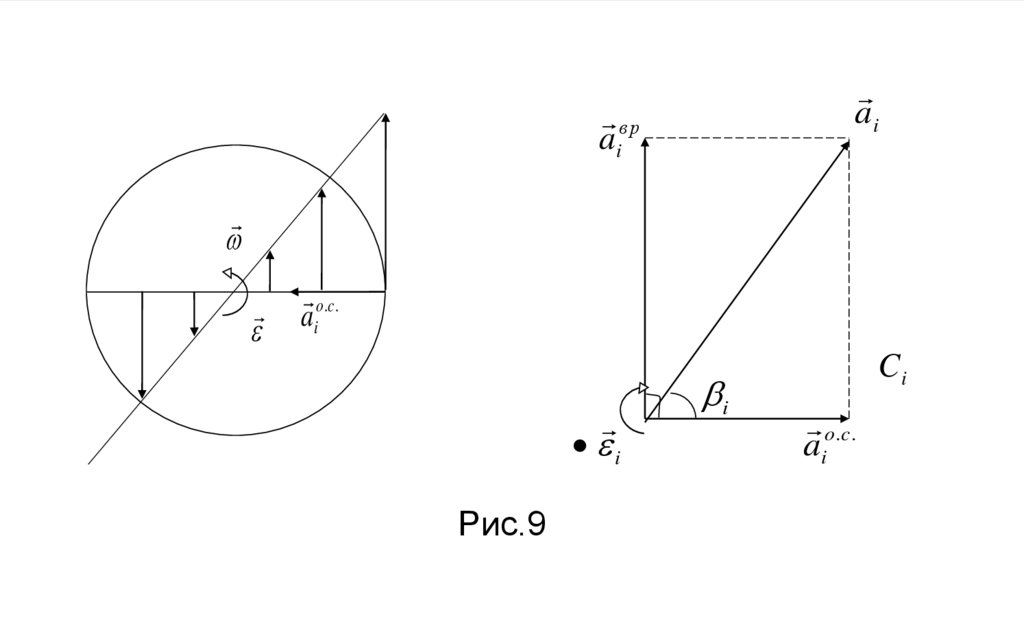
§4.3.3. Распределение скоростей и ускорений точек
твердого тела при его вращении вокруг оси.
Рассмотрим сечение твердого тела, вращение вокруг оси в
плоскости, которой лежит траектория i-й точки (Рис.9).
Vi d i
вр
ос
a
d
a
dm
вр
ос
2
m
m
m
ai d i , ai d i , вр , ос
ak d k ak d k
аiвр
tg i o.c. 2 i
аi
ai
вр 2
o.c 2
ai
ai
di
2 4

13.

ai
вр
ai
o.c.
ai
i
Рис.9
i
Ci
aio.c.

14.

§4.4. Преобразование движения из вращательного
во вращательное.
Передаточные механизмы предназначены для
передачи вращения от одного вала, называемого
ведущим, к другому валу, называемым ведомым.
Если оси ведущего и ведомого валов параллельны или
пересекаются, то вращение можно передать при помощи
фрикционной или зубчатой передачи. В случае фрикционной
передачи вращение передается вследствие действия сил
сцепления между находящимися в контакте поверхностями. В
зубчатой передаче – через сцепления зубьев.

15.

Кроме фрикционной и зубчатой передач, существуют
передачи на расстоянии при помощи гибкой связи: ремня,
троса, цепи. В технике применяются и передачи из серии
колес с неподвижными осями вращения в виде
последовательного ряда с паразитными колесами и
последовательного ряда с кратным зацеплением. Их
называют рядовыми передачами. Варианты передач и
передаточных механизмов представлены далее и в
Приложении № 7. В основе инженерного кинематического
расчета этих передач лежат условия зацепления (сцепления)
без проскальзывания и понятие о передаточном числе и
передаточном отношении.

16.

§4.4.1. Условия зацепления (сцепления) без
проскальзывания.
В точке зацепления k двух тел при отсутствии
проскальзывания должны быть равны
Vk 1 V k 1
a kвр1 a kвр2
При этом внешнее зацепление меняет знак угловой
скорости, внутреннее — сохраняет.
(35)

17.

§4.4.2. Передаточное число, передаточное отношение.
Отношение модуля i-го вала (колеса), к модулю j-го
вала (колеса), называется передаточным числом i, а с
учетом знака угловой скорости – передаточным
отношением I.
i i
ii j
;
j j
i
k
Ii j 1
1 ii j
j
Здесь k – число внешних зацеплений.
k
(34)

18.

– число внешних зацеплений.
Передаточные число и отношение можно выразить как через
отношение угловых скоростей и отношение радиусов колес
r, так и через число оборотов в минуту n вала или шестерни
и число зубьев z колес. Действительно, если z – число зубьев
колеса а h – шаг зуба, то 2 r h z и
h
r
z
2
(35)
С другой стороны обороты в минуту (n) и радианы в секунду
( ω) связаны между собой между собой простым соотношением: (n / 60) 2 . То есть
30
n

19.

Поэтому, (34) можно переписать так
ni
ii j
nj
k ni
I i j 1
nj
1 ii j
k
К этому материалу студенты должны добавить
самостоятельное конспектирование №1 (см. календарный
план)

20.

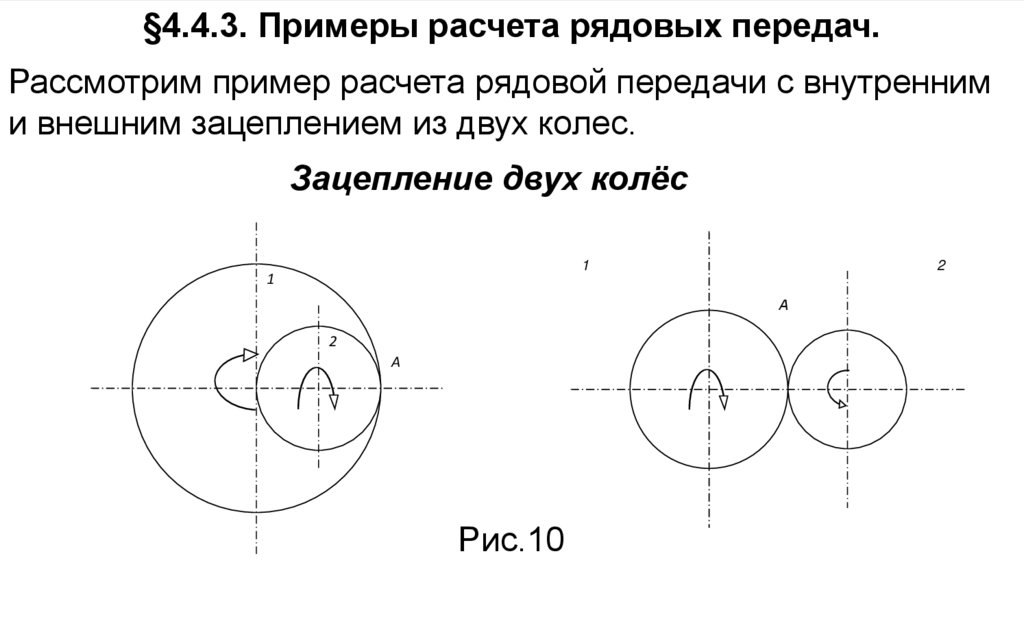
§4.4.3. Примеры расчета рядовых передач.
Рассмотрим пример расчета рядовой передачи с внутренним
и внешним зацеплением из двух колес.
Зацепление двух колёс
1
1
2
А
2
А
Рис.10

21.

Исходя из условия зацепления без проскальзывания, имеем
1 r1 2 r2
Учитывая, что число z-зубцов в колесах пропорциональны их
радиусам, а вращение происходит при внутреннем сцеплении
в одну сторону, а при внешнем в разные, получаем .
1
r2 z2
внеш.
; 1 внутр. r2 z2
2
r1
z1
2
r1
z1

22.

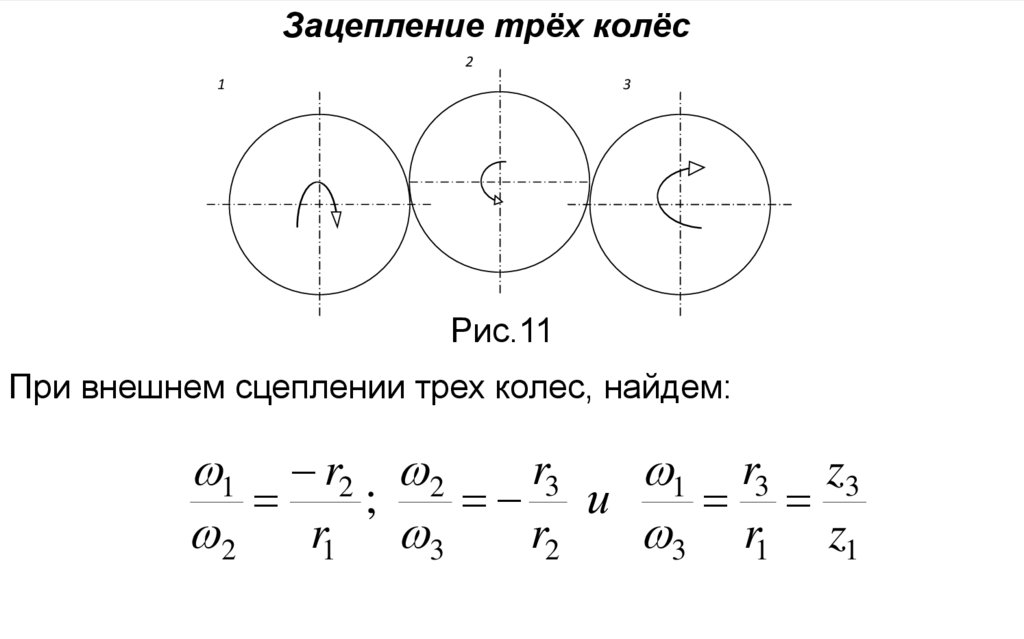
Зацепление трёх колёс
2
1
3
Рис.11
При внешнем сцеплении трех колес, найдем:
r3
1 r2 2
1 r3 z3
;
и
2
r1 3
r2
3 r1 z1

23.

Отношение угловых скоростей шестерен обратно
пропорционально их радиусам и не зависит от радиусов
промежуточных шестерен.
k rn
k zn
1
При рядовом сцеплении:
1
1
n
r1
z1
к – число внешних зацеплений.Так, например, с учетом (34) –
(37) и условия зацепления без проскальзывания (33) для
передачи с кратным зацеплением, представленной на
Рис. 12.
2
1
получим:
VK 1
r1 r2 z 2
1
i1 2
2 Vk 2 r1 z1
r
2
(38)
Рис.12