Кинематика произвольного движения твердого тела

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция 12.
Кинематика произвольного движения твердого
тела.
§ 12.1. Первая общая теорема кинематики твердого тела.
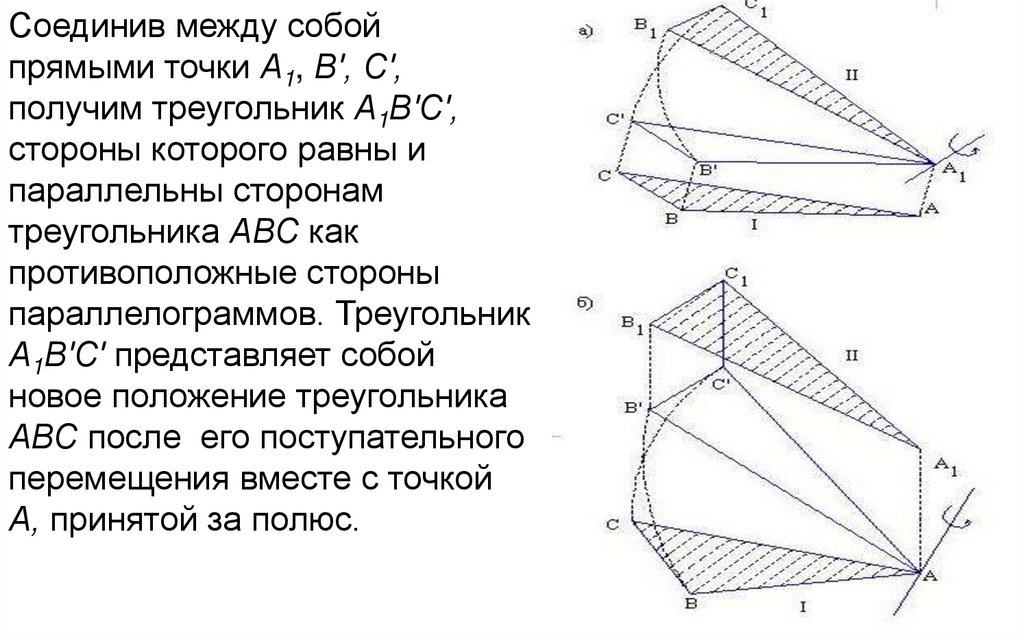
Соединяя эти точки между собой прямыми, получаем
треугольник. Движение твердого тела в пространстве можно
изучить как движение треугольника, определяющего его
положение.
Предположим, что треугольник АВС определяет положение
некоторого тела. Рассмотрим перемещение треугольника АВС
в новое положение А1В1С1. Осуществим это перемещение как
совокупность двух перемещений. Для этого соединим одну из
вершин, например А, с ее новым положением А1. Затем
проведем отрезки ВВ' и СС', равные и параллельные отрезку
АА1 (рис. 53 а).

3.

Соединив между собой
прямыми точки А1, В', С',
получим треугольник А1В'С',
стороны которого равны и
параллельны сторонам
треугольника АВС как
противоположные стороны
параллелограммов. Треугольник
А1В'С' представляет собой
новое положение треугольника
АВС после его поступательного
перемещения вместе с точкой
А, принятой за полюс.

4.

Согласно теореме Эйлера —Даламбера для перемещения
треугольника из положения А1В'С' в положение А1В1С1
произведем поворот треугольника на некоторый угол вокруг
оси, проходящей через точку А1, которая не участвует в
перемещении.

5.

§ 12.2 Теорема Шаля
Таким образом, установлено, что всякое перемещение
свободного твердого тела из одного положения в другое
можно осуществить совокупностью двух перемещений:
поступательного вместе с точкой, принятой за полюс, и
поворота тела вокруг некоторой оси, проходящей через
полюс. На рис. 53а и б показано, что результирующее
перемещение тела не зависит от последовательности, в
которой осуществляются составляющие перемещения.
Перемещение треугольника из положения АВС в положение
А1В1С1 (рис. 53, б) можно осуществить путем поворота его
вокруг оси, проходящей через точку А, до положения АВ'С', в
первую очередь, и поступательного перемещения вместе с
полюсом А из положения АВ'С' в положение А1В1С1 — во
вторую очередь.

6.

Очевидно, что совокупность этих двух перемещений не
отображает действительного движения твердого тела, а
позволяет лишь осуществить перемещение твердого тела из
первого положения во второе.
При действительном движении свободного твердого тела
составляющие движения этого тела совершаются
одновременно, т.е. движение свободного твердого тела
можно рассматривать как сложное, состоящее из
поступательного движения вместе с некоторой точкой
тела, принятой за полюс, и сферического движения вокруг
этого полюса.

7.

8.

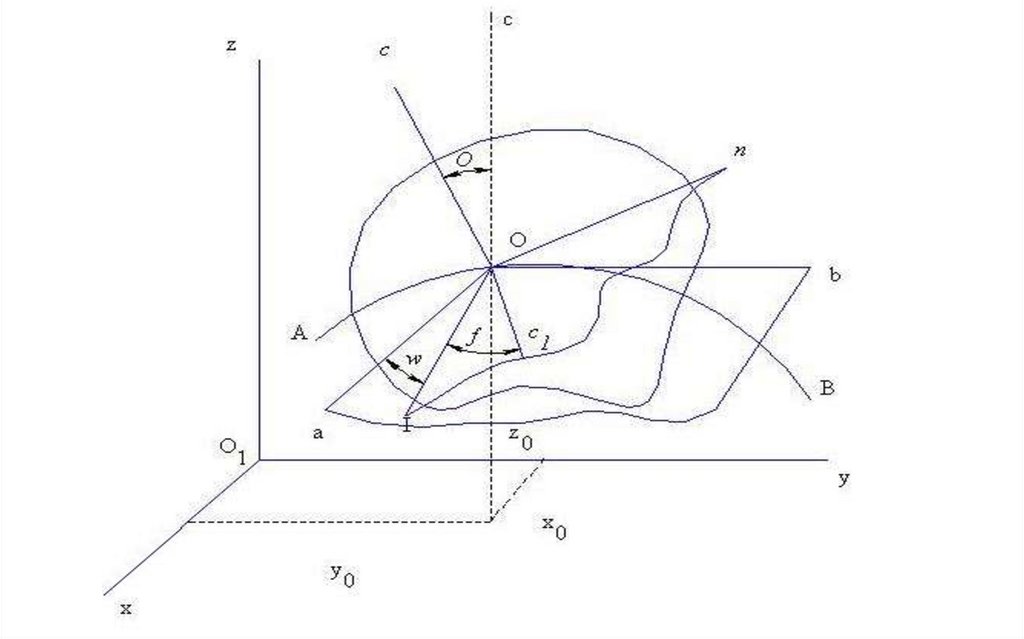
Примем произвольную точку О за полюс и покажем
траекторию полюса АВ (рис. 54). Поступательная часть
движения твердого тела определяется движением полюса О.
Обозначив координаты полюса О в неподвижной системе
осей декартовых координат хо, уо, zо, получим уравнения
движения.
x0=f1 (t),
y0=f2 (t),
z0=f3 (t).

9.

Сферическое движение твердого тела можно определить
заданием эйлеровых углов как функций времени. Для
определения эйлеровых углов проведем три взаимно
перпендикулярные оси а, b, c , движущиеся поступательно
вместе с точкой О и остающиеся параллельными
неподвижным осям x, у, z, а также взаимно
перпендикулярные оси ξ, η, ζ, связанные с телом.
Определив при помощи этих осей эйлеровы углы ψ, θ, φ,
напишем три уравнения сферического движения тела вокруг
полюса О:
ψ=f4 (t),
θ=f5 (t),
φ=f6 (t).

10.

Таким образом, движение свободного твердого тела
определяется шестью уравнениями, называемыми
уравнениями движения свободного твердого тела:
x0=f1 (t),
y0=f2 (t),
z0=f3 (t),
ψ=f4 (t),
θ=f5 (t),
φ=f6 (t).
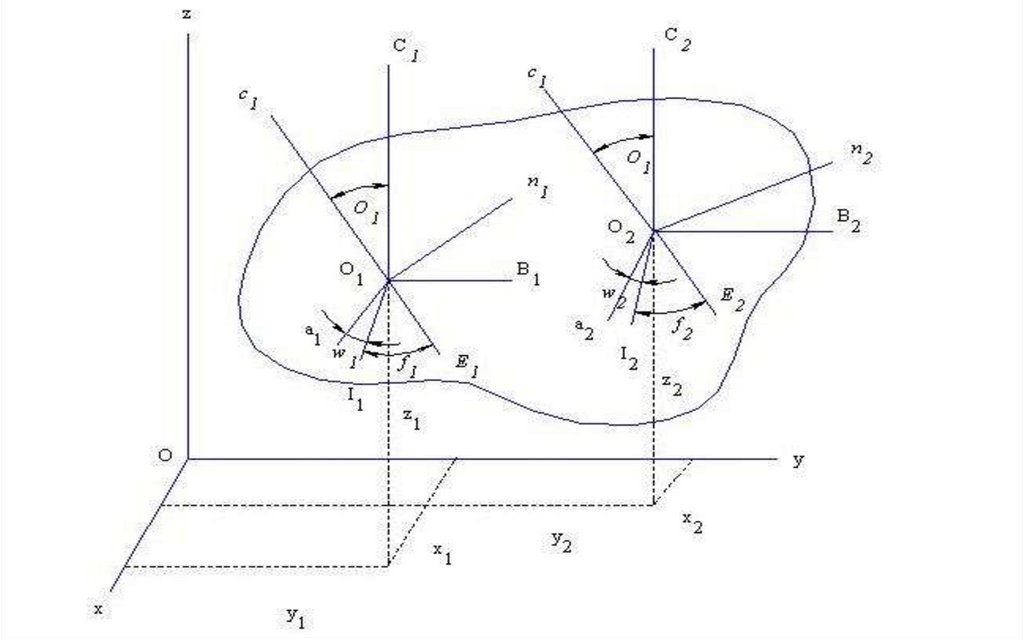
Положение свободного твердого тела определяется заданием
шести независимых величин x0, y0, z0,, ψ, θ, φ; следовательно,
свободное твердое тело имеет шесть степеней
свободы. Вид первых трех уравнений, определяющих
поступательную часть движения твердого тела, зависит от
выбора полюса, так как координаты различных точек тела
различны (рис. 55). Вид остальных трех уравнений,
определяющих сферическое движение твердого тела вокруг
полюса, от выбора полюса не зависит.

11.

12.

Действительно, если связать с телом две системы О1ξ1η1ζ1 и
О2ξ2η2ζ2, оси которых соответственно параллельны, то эта
параллельность сохранится при движении тела и эйлеровы
углы при полюсах О1 и О2 будут одинаковы.
Положение тела будет известно, если будем знать положение
точки А.
x1A f1 (t ) y1A f 2 (t ) z1 A f3 (t )
f 4 (t ) f5 (t ) f 6 (t )
Первые три уравнения определяют то движение, которое
тело совершало бы при постоянных углах , т.е. при
поступательном движении тела вместе с полюсом А.
Последние три определяют движение, которое происходило
бы при постоянных значениях координат , т.е. когда точка А
неподвижна.

13.

Р
А
Движение свободного твердого тела можно рассматривать как
слагающиеся из поступательного движения, при котором все
точки тела движутся как произвольно выбранный полюс А со ,
и из серии элементарных поворотов с угловой скоростью
вокруг мгновенных осей вращения, проходящей через полюс
А. Основными кинематическими характеристиками являются
полюса, определяющего поступательной части движения, а
так же вращения вокруг полюса.