Логарифмические уравнения. Основные приемы их решения

1. «Логарифмические уравнения. Основные приемы их решения»

2.

«Ничему тому, что важно
знать, научить нельзя, всё, что может сделать
учитель, это указать
дорожки»
Ричард
Олдингтон
(1892 – 1962гг..) английский поэт,
прозаик, критик
«Кто говорит – тот сеет, кто
слушает – тот собирает».
Русская народная пословица

3. Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.

Уравнение, содержащее неизвестное под знаком логарифма или (и) в
его основании, называется логарифмическим уравнением.
1. Решение логарифмических
определения логарифма.
Определение логарифма:
уравнений
на
основании
log a b c : a c b, a 0, b 0, a 1.
log a f ( x ) c f ( x ) a c ,
f ( x ) 0, a 0, a 1.
Пример 1:
log 4 x 2,
ОДЗ : х 0,
x 42 ,
x 16.
Ответ: 16.

4.

Пример 2:
Пример 3:
log 3 (2 x 1) 2,
4x 3 5,
2 x 1 32 ,
2 x 1 9,
x 4.
x 3 log 4 5,
Проверка:
log 3 (2 4 1) 2,
log 3 9 2,
2 2
Ответ: 4.
х 3 log 4 5.
Ответ:
3 log 4 5.

5.

log g ( x ) f ( x) c f ( x) g ( x) c ,
f ( x ) 0, g ( x ) 0, g ( x ) 1.
Пример 4:
ОДЗ:
log x 1 ( 2 x 2 1) 2,
2 x 2 1 0,
x 1 0,
x 1 1,
x ( 1;0) (0; )
log x 1 ( 2 x 2 1) 2,
2 x 2 1 ( x 1) 2 ,
2 x 2 1 x 2 2 x 1,
x 2 2 x 0,
x ( x 2) 0,
x1 0, x2 2.
Ответ: 2.

6.

2. Метод потенцирования.
Под потенцированием понимается переход от равенства, содержащего
логарифмы, к равенству, не содержащему их.
log a f ( x ) log a g ( x ) f ( x ) g ( x ), где a 0, a 1, f ( x ) 0, g ( x ) 0.
Пример 5:
log 2 ( x 2 7 x 5) log 2 (4 x 1),
x 2 7 x 5 4 x 1,
x 2 3x 4 0,
x1 1, x2 4.
Проверка:
x 1 log 2 (12 7 1 5) log 2 (4 1 1) log 2 3 log 2 3 - верно
2
x 4 log 2 (( 4) 7 ( 4) 5) log 2 (4 ( 4) 1) log 2 ( 17) log 2 ( 17)
- не верно
Ответ: 1.

7.

log h ( x ) f ( x ) log h ( x ) g ( x ) f ( x ) g ( x )
f ( x ) 0, g ( x ) 0, h( x ) 0, h( x ) 1.
Пример 6:
log 2 x ( x 2 7 x 5) log 2 x ( 4 x 1),
x 2 7 x 5 4 x 1,
ОДЗ:
x 2 3x 4 0,
x1 1, x2 4.
x 2 7 x 5 0,
4 x 1 0,
2 x 0,
2 x 1.
Проверка:
x 1 log 2 1 (12 7 1 5) log 2 1 (4 1 1) log 3 3 log 3 3
1 1 верно.
x 4 log 2 4 (( 4) 2 7 ( 4) 5) log 2 4 (4 ( 4) 1)
log 2 ( 17) log 2 ( 17) не верно
Ответ: 1.

8.

Пример 7:
1 log 4 41
log 4 (4 7 x) log 4 (1 5x) 1.
получим
log c a log c b log c ab
log 4 (4 7 x) log 4 (1 5x) log 4 4,
log 4 (4 7 x) log 4 ((1 5x) 4),
4 7 x 4(1 5 x ),
x 0.
Проверка:
log 4 (4 7 0) log 4 (1 5 0) 1,
log 4 4 log 4 1 1,
1 1
верно
Ответ: 0.

9.

3. Метод подстановки.
Пример 8:
log 32 x log 3 x 2
ОДЗ:
Пусть
log 3 x t ,
x 0.
тогда
t 2 t 2, t 2 t 2 0.
t1 1, t2 2.
Значит,
log 3 x 1
или
log 3 x 2
x 3 1
x 32
1
x .
3
x 9.
1
, 9.
Ответ:
3

10.

a log
2
g( x)
f ( x) b log g ( x ) f ( x) c 0
f ( x ) 0, g ( x ) 0, g ( x ) 1, a, b, c числа, а 0.
Пример 9:
log 7 x log x 7 2,5
x 0,
ОДЗ:
x 1.
log a b
1
log b a
1
5
.
log 7 x 2
1 5
Подстановка: t log 7 x. Уравнение примет вид: t ,
t 2
2t 2 5t 2 0,
Приведём логарифмы к одному основанию – 7:
log 7 x
t1 2, t 2
Значит,
log 7 x 2
x 72 ,
x 49.
или
1
.
2
1
log 7 x
2
1
x 72 ,
x 7.
Ответ:
7 , 49.

11.

4. Метод логарифмирования.
f ( x ) g ( x ) log h ( x ) f ( x ) log h ( x ) g ( x )
f ( x ) 0, g ( x ) 0, h( x ) 0, h( x ) 1.
Пример 10:
x
log3 x 4
log 3 ( x log3 x 4 ) log 3
Пусть
Значит,
x 0,
ОДЗ: x 1.
1
,
27
1
27,
(log 3 x 4) log 3 x 3.
log 3 x t ,
тогда
log 3 x 1
x 3,
x 3.
1
log c a p p log c a
(t 4)t 3,
t 2 4t 3 0,
t1 1, t2 3.
log 3 x 3,
или
x 33 ,
x 27.
Ответ: 3; 27.

12. Выводы:

1.На основании определения логарифма.
2.Метод потенцирования.
3.Метод постановки.
4.Метод логарифмирования.

13. «Логарифмические неравенства. Основные приемы их решения»

14.

По определения логарифма
Простейшие логарифмические неравенства
записывается следующим образом:
log a f ( x) b log a f ( x) b
Схема сравнения логарифмических неравенств.
logа x > b
0<a<1
0 < x < ab
logа x <
b
a>1
0<a<1
a>1
x > ab
x > ab
0 < x < ab

15.

Метод потенцирования
Суть метода в следующем: с помощью формул
неравенство привести к виду
log a f ( x) log a g ( x)
Справедливы следующие утверждения:
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, a 1
g ( x) 0;
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, 0 a 1
g ( x) 0;

16.

Метод подстановки
Ищем в неравенстве некоторое повторяющееся
выражение,
которое
обозначим
новой
переменной,
тем
самым,
упрощая
вид
неравенства. В некоторых случаях, очевидно что
удобно обозначить.

17.

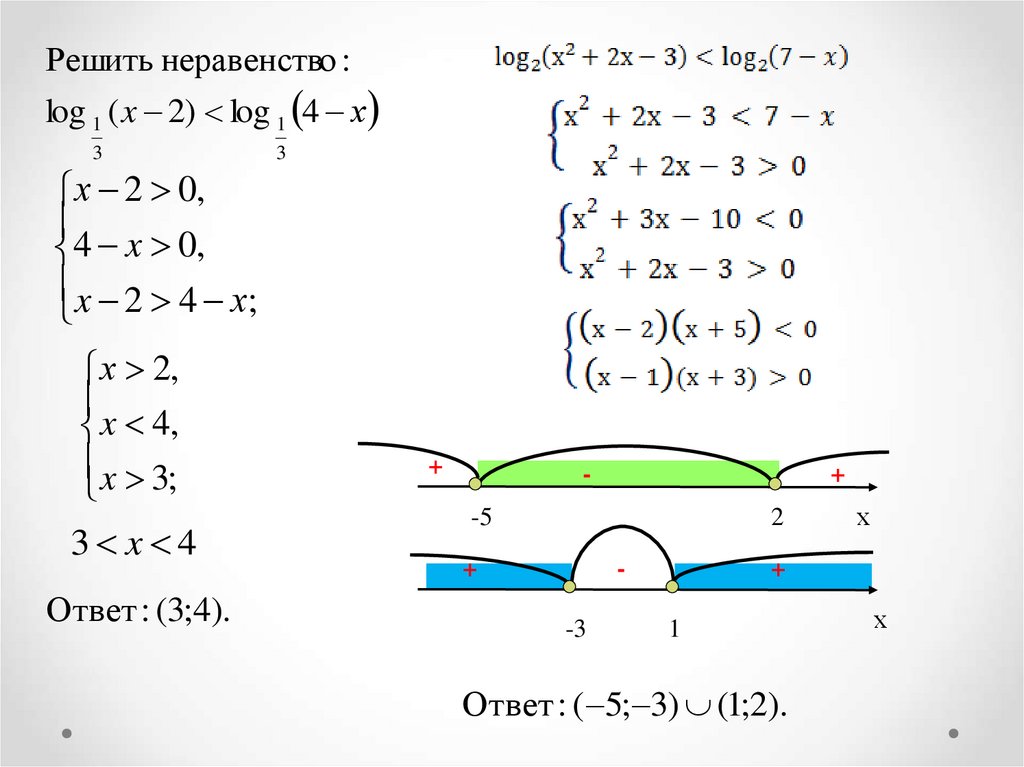
Решить неравенство :
log 1 ( x 2) log 1 4 х
3
3
х 2 0,
4 x 0,
x 2 4 х;
х 2,
x 4,
x 3;
3 x 4
Ответ : (3;4).
+
-
+
-5
2
+
-3
х
+
1
Ответ : ( 5; 3) (1;2).
х

18. Спасибо за внимание!

Удачи !
Успехов!