Вращательная энергия молекул

1. Вращательная энергия молекул

В системе главных осей инерции a, b, c:
N
N
N
i
i
i
mi ai = mi bi = mi ci = 0
N
N
N
i
i
i
mi bi ci = mi ai bi = mi ai ci = 0
mi – масса, ai, bi, ci – координаты i–того атома в системе главных осей инерции.
Pa2
Pb2
Pc2
Tr
,
2I a 2I b 2I c
Кинетическая энергия вращения жесткой молекулы:
P 2 Pa2 Pb2 Pc2
Pa , Pb , Pc – проекции полного углового момента количества движения P:
N
i
В операторном виде
2
a
2
b
2
c
T Hr A P B P C P ,
N
I a m r , I b m r , I c mi ric2
I a , I b , I c – моменты инерции относительно главных осей:
2
N
2
i ia
где
A
2
i ib
i
h
h
h
C
,
B
,
8 2 I a
8 2 I c
8 2 I b
Решение уравнения Шредингера
H r r E r r
Принято выбирать
i
обусловлено типом молекул и зависит от
соотношения величин моментов инерции
Ia Ib Ic

2.

Типы волчков. I
1. Двухатомные и линейные молекулы
I a 0, I b I c , оси b и с перпендикулярны оси молекулы.
Правило отбора
J 1,
Энергия:
Er hBJ ( J 1)
вид спектра определяется:
hB( J 1)( J 2) hBJ ( J 1)
2 B( J 1)
h
Будут иметь молекулы с дипольным моментом симметрии
C n , C nv , C s , C v
2. Молекулы типа сферического волчка (нет дипольного момента)
I a Ib Ic ,
Энергия:
Er hBJ ( J 1),
3. Молекулы типа симметричного волчка
система уровней та же, но дипольные переходы
запрещены
(одна ось Сn порядка выше второго, два момента
инерции равны)
a)
Ia Ib Ic
и
A B C
– вытянутый волчок, ось а совпадает с осью Сn ,(CH3Cl)
б)
I a Ib Ic
и
A B C
– сплюснутый волчок, ось с совпадает с осью Сn ,(CHCl3)

3. Типы волчков. II

Энергия для вытянутого волчка
Erвыт h[ BJ ( J 1) ( A B) K 2 ]
Энергия для сплюснутого волчка
Erспл h[ BJ ( J 1) (C B) K 2 ]
Правило отбора для K
K 0,
J 1
правило отбора для J
4. Молекулы типа ассиметричного волчка
Ia Ib Ic
и
A B C.
2B A C
Параметр асимметрии:
A C
1
а) для вытянутого волчка
б) для сплюснутого волчка
Энергия вращения:
Erасим
1
( A C)
( A C) J
hJ ( J 1)
hE (κ )
2
2
E J ( ) – функция только параметра асимметрии κ.
Для данного J имеются 2J+1 значение функций E J ( ), задаваемых числом , которое изменяется от –J до+J

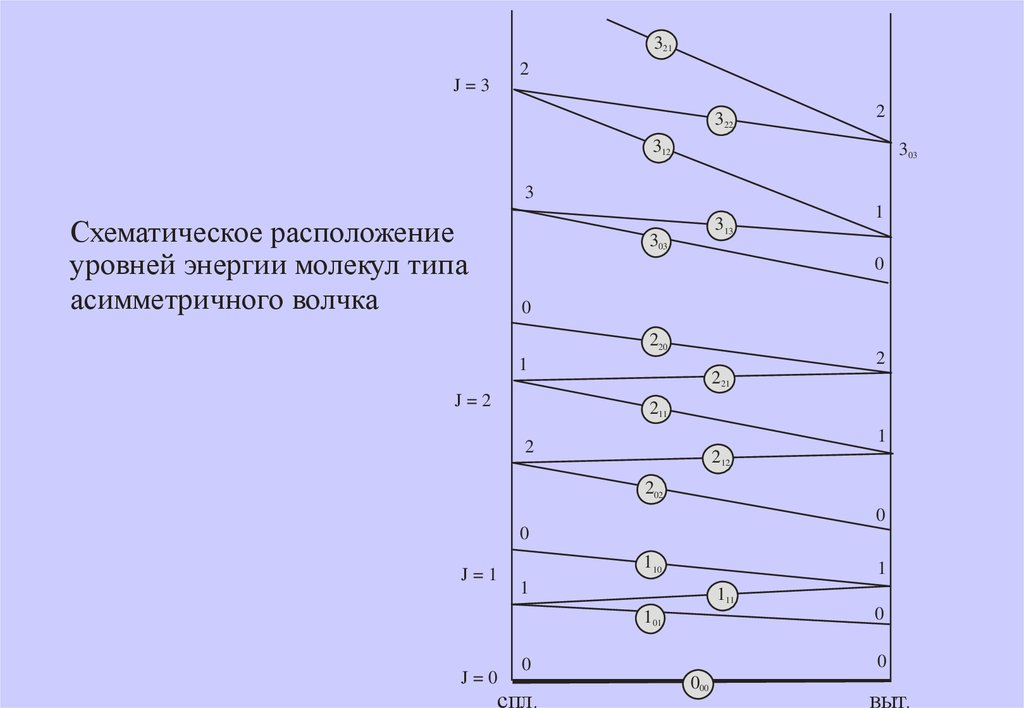
4.

321
2
J=3
322
2
312
303
3
Схематическое расположение
уровней энергии молекул типа
асимметричного волчка
313
303
1
0
0
220
2
1
J=2
221
211
1
2
212
202
0
0
J=1
110
1
1
111
0
101
J=0
0
0
спл.
000
выт.

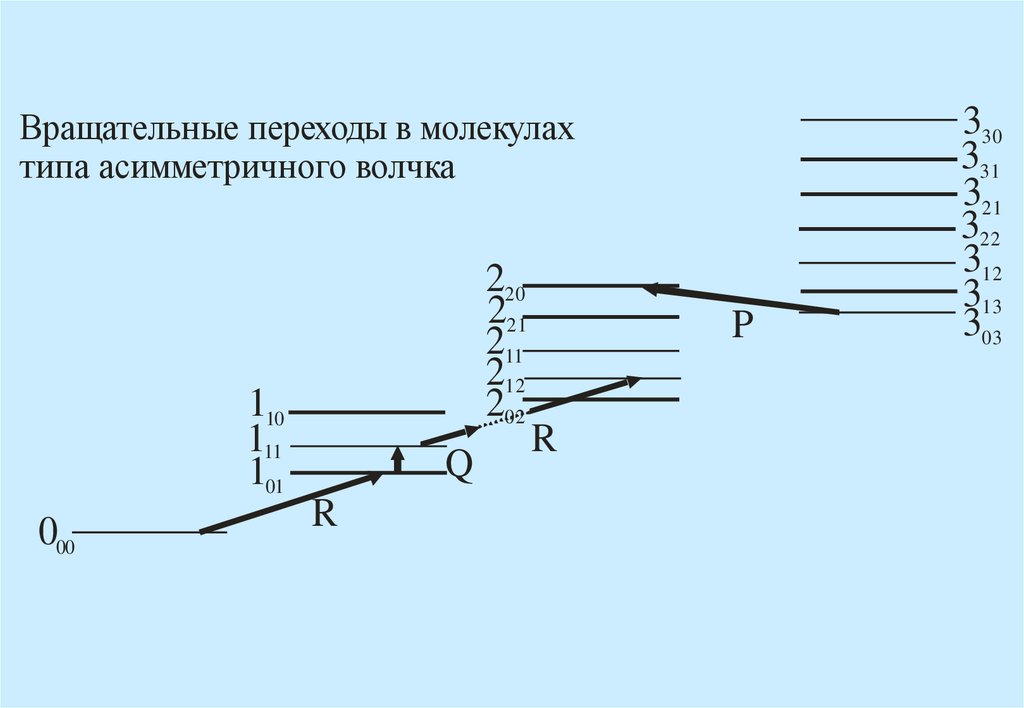
5.

Вращательные переходы в молекулах
типа асимметричного волчка
220
221
211
212
202
110
111
101
000
Q
R
P
R
330
331
321
322
312
313
303

6. Эффект Штарка

В однородном электрическом поле наблюдается расщепление вращательных
линий. Вращательная энергия молекулы в этом случае зависит от
напряженности поля и собственного дипольного момента и магнитного
квантового числа M. Следовательно, частоты наблюдаемых переходов тоже
будут от них зависеть. Например, для симметричного волчка:
2MK 0 0
2 B( J 1)
J ( J 1)( J 2)h
где M - магнитное квантовое число, принимающее значения от J до J , а правила
отбора - J 1, K 0, M 0 .

7. Влияние колебаний молекул и центробежного растяжения на вращательные постоянные

Вращательные постоянные зависят от колебательного состояния, в
котором находится молекула
ds
B Bv Be (vs )
2
s
b
s
В приближении нежесткого ротатора выражение для энергии:
E hc[ Вv J ( J 1) Dv J 2 ( J 1) 2 ]
где
Dv
- постоянная центробежного
искажения

8. Расчет геометрических параметров молекул

re – структура,
1
1
(
v
);
Bv Be 1 (v1 ) 2 (v2 1)
3
3
2
2
r0 – структура,
в простейшем случае двухатомной молекулы XY:
=
2 B0 ( J 1) B0
rz – структура,
h
2
I
m
r
2
0
i 0i
0 XY
8 cI 0
1
Bz B0 bs ( гарм) d s ;
2 s
rs – структура.
r

9. Внутреннее вращение

Потенциальная энергия принимается в виде:
V ( )
V0
(1 cos n )
2
(для решения уравнения Шредингера используют модель плоского ротатора).
k 2 0
, то частота кр
Если потенциальная энергия крутильных колебаний V ( )
2
1 kI M
2 I 1I 2
где I1 и I2 - моменты инерции внутренних волчков около центральной связи, IM -= I1 + I2
При малых изменениях потенциал внутреннего вращения:
V0
V0
V0 n 2 2
n 2 2
V ( ) (1 cos n ) (1 1
...)
,
2
2
2
4
.
поэтому
кр
n V0 I M
.
2 2 I 1I 2
E
Частоту крутильного колебания можно определить из
I 1 N1 g1 kT
e
I 0 N 0 g 0

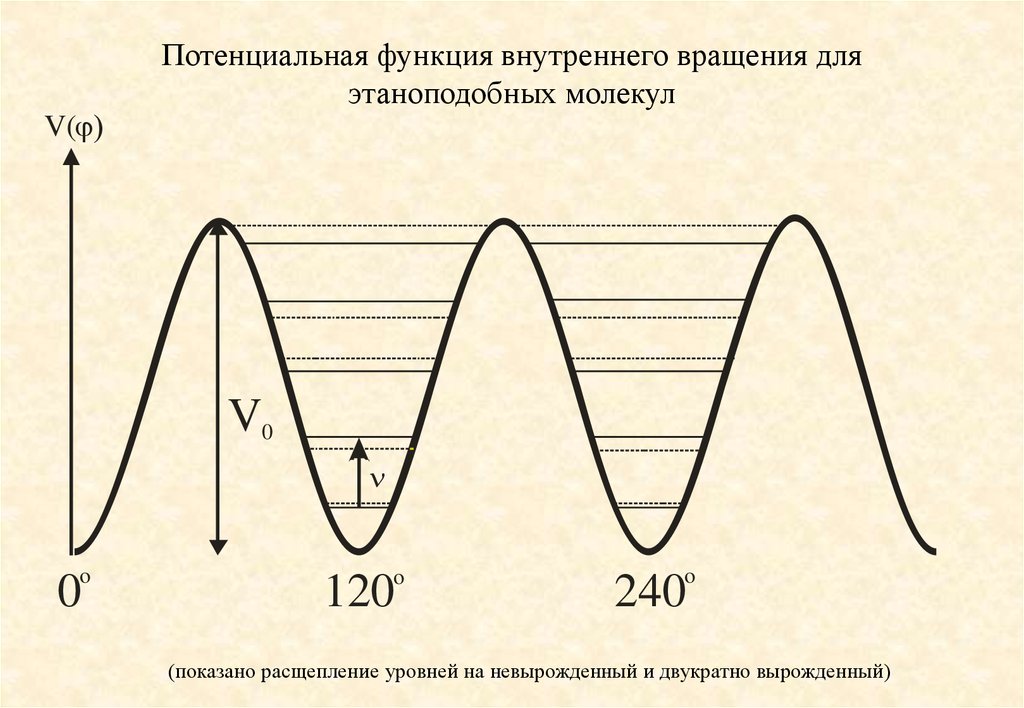
10. Потенциальная функция внутреннего вращения для этаноподобных молекул

V( )
V0
o
0
o
120
o
240
(показано расщепление уровней на невырожденный и двукратно вырожденный)

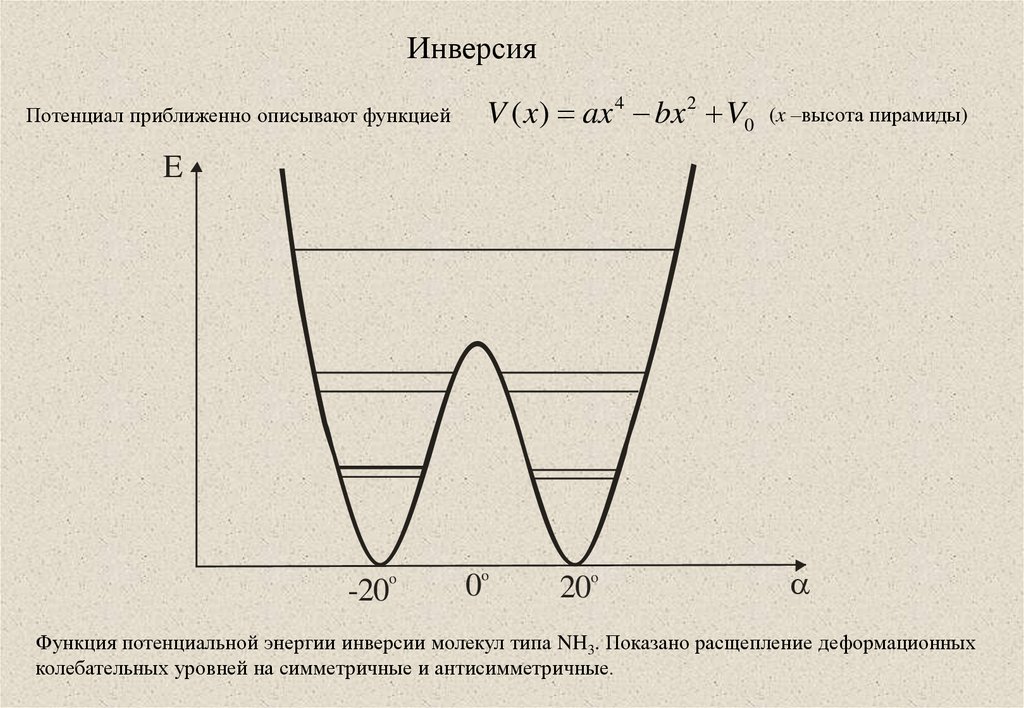
11. Инверсия

Потенциал приближенно описывают функцией
V ( x) ax 4 bx 2 V0
(x –высота пирамиды)
E
o
-20
0o
20o
Функция потенциальной энергии инверсии молекул типа NH3. Показано расщепление деформационных
колебательных уровней на симметричные и антисимметричные.