Поляризуемость. Эллипсоид поляризуемости и симметрия молекулы

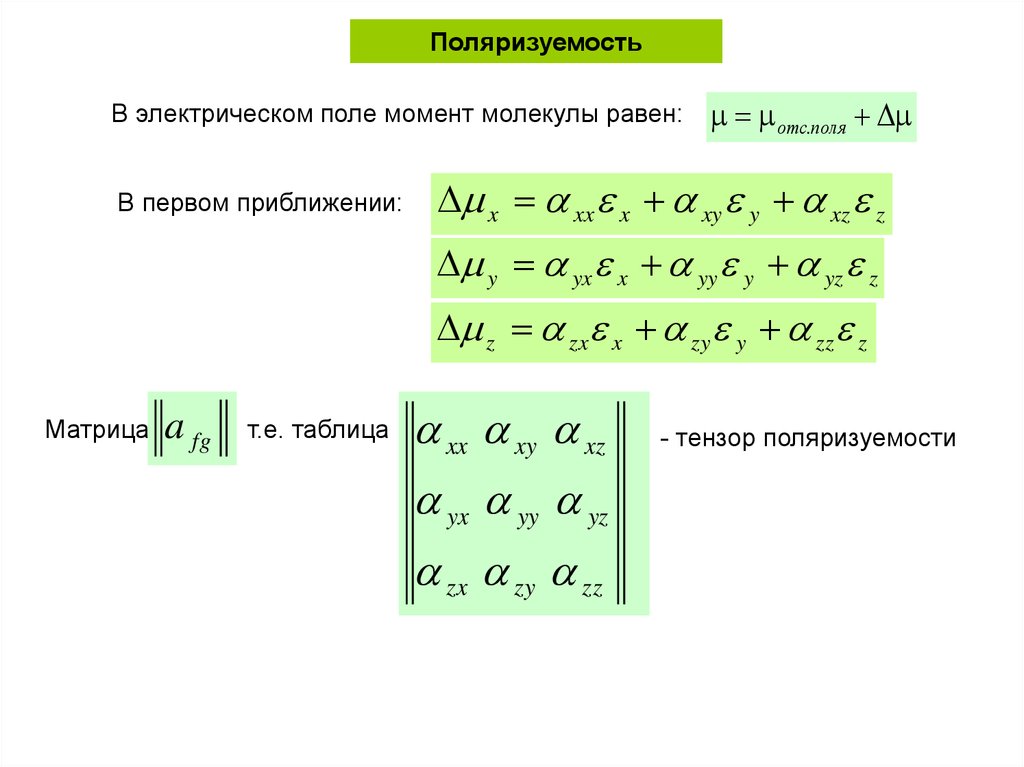
1. Поляризуемость

В электрическом поле момент молекулы равен:
В первом приближении:
отс.поля
x xx x xy y xz z
y yx x yy y yz z
z zx x zy y zz z
Матрица
a fg
т.е. таблица
xx xy xz
yx yy yz
zx zy zz
- тензор поляризуемости

2.

Тензор в системе главных осей поляризуемости молекул:
При этом проекции на главные
оси поляризуемости:
Y YY Y
XX 0 0
0 YY 0
0 0 ZZ
X XX X
Z ZZ Z
_
Средний дипольный момент:
В общем случае
0 cos 2 0t ,
тогда
Размерность:
- напряженность статического
0поля
( 0 )
{ } заряд длина длина 2
{ }
длина 3
{ }
заряд

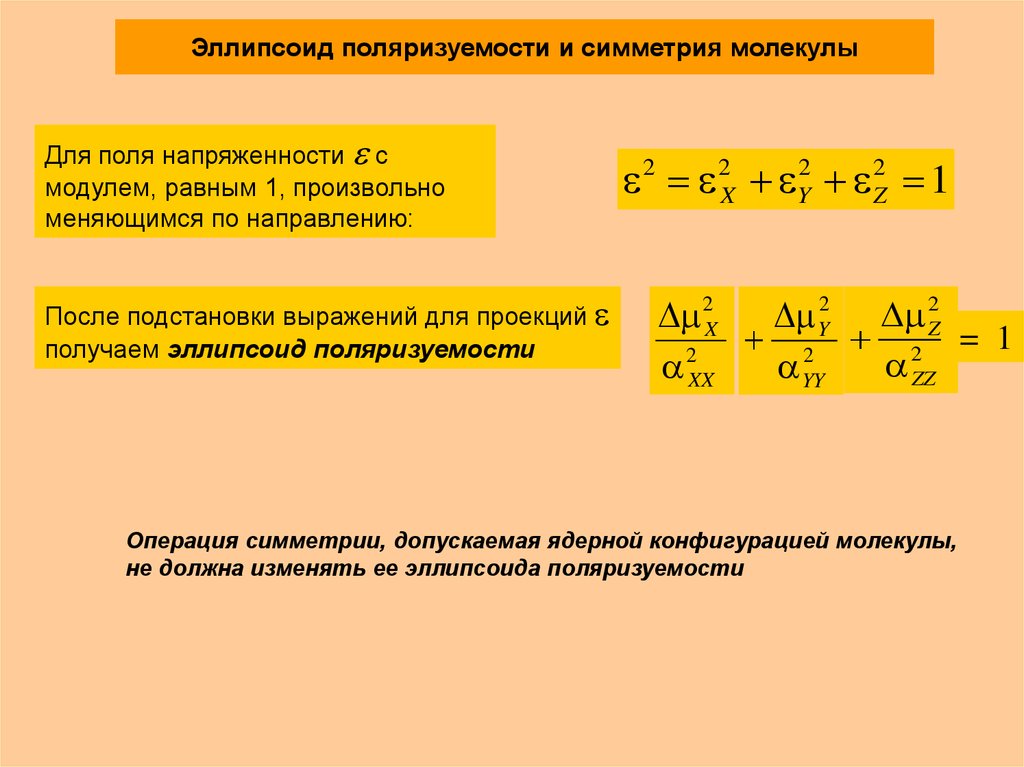
3. Эллипсоид поляризуемости и симметрия молекулы

Для поля напряженности с
модулем, равным 1, произвольно
меняющимся по направлению:
После подстановки выражений для проекций
получаем эллипсоид поляризуемости
1
2
2
X
2
Y
2
Z
2X
Y2 2Z
2 2 = 1
2
ZZ
XX
YY
Операция симметрии, допускаемая ядерной конфигурацией молекулы,
не должна изменять ее эллипсоида поляризуемости

4. Энергия молекулы во внешнем электрическом поле

U r 0 cos
Энергия поворота для жесткого диполя:
где
- угол между вектором диполя и направлением поля.
2
Энергия поляризации (деформации): U D d d D
D
2
0
0
(средняя составляющая собственных моментов направлена по полю)
Полная энергия : U
Ur UD
D 2
0 cos
2

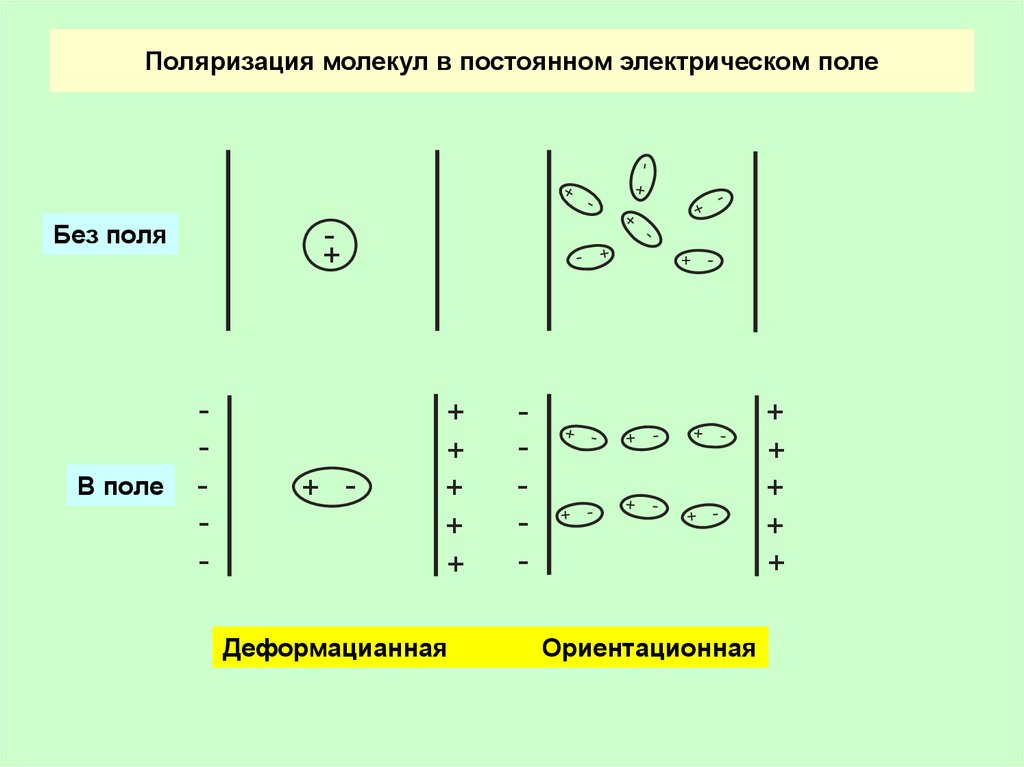
5. Поляризация молекул в постоянном электрическом поле

+
Без поля
-
+ -
+
+
+
+
+
+
+
Деформацианная
-
-
-
+ -
В поле
+
-
+ -
Поляризация молекул в постоянном электрическом поле
+ -
+ -
+ -
+ -
+ -
+ -
+ -
Ориентационная
+
+
+
+
+

6. Ориентационная поляризация молекулы

Основные допущения:
1) плотность газа настолько низка, что энергия диполь-дипольного взаимодействия
мала по сравнению с тепловой энергией (~kT);
2) поле не оказывает возмущающего действия на дипольный момент молекулы;
3) энергия молекулы в поле мала по сравнению со средней тепловой энергией молекулы.
Поляризация газа:
0 cos D
02
D
После усреднения:
3kT
02
Ориентационная поляризуемость молекулы: r
3kT
В этом случае
Оценка вклада
( r D ) r D
r для T 300 K , 105 В / см, 0 3.34 10 30 Кл м
r 0
10 2 10 3
0 3kT

7. Поляризация диэлектрика в переменном поле. Мольная рефракция

Диэлектрик в электрическом поле конденсатора:
E
E0
s
0
Уравнение Клаузиуса-Моссотти для неполярных диэлектриков для которых
D
1
1
n ,
2 3 0
1
M
1
N A
2
3 0
Уравнение Ланжевена-Дебая:
(для полярных диэлектриков)
Уравнение Лоренца-Лоренца:
(для неполярных диэлектриков
в переменом электрическом поле
высокой частоты)
где n
N A - число молекул в 1 м3.
M
(в традиционной форме)
02
M
1
PM
N A ( D
)
2
3 0
3kT
1
2
n
1 M
1
t
Rv 2
N Ab
n 2 3 0
(b - электронная поляризуемость в переменном электрическом
( ) n ( ),
поле высокой частоты,
n – показатель
преломления, при экстраполяции к n b стремится к статической
электронной молярной поляризуемости e )
2

8. Энергия образования молекул в классической теории

Для энергии образования моля вещества из свободных атомов:
EM U M ( г, ат) U пр.в. U M ( г )
Для энтальпий
H M ( г, ат) H пр.в. H M ( г )
Согласно классической теории:
_
M Э
Э
( Э Э )'' ...
Э Э ( Э Э )' ( Э
Э )''
( Э Э )'
Э Э
_
Это выражение приводится к виду
IJ IJ
M nuv
uv
I , J uv
IJ
nuv
– число связей в молекуле вида ( ЭI Э J ) ( где I, J отражают валентное
IJ
состояние и первое окружение каждого атома); uv
– эффективная парциальная
величина энергии образования, сопоставляемая связи этого вида.
Для моля молекул
EM
I ,J
nuvIJ EuvIJ
uv
и
H M ( г, ат)
I ,J
IJ
IJ
n
H
uv uv
uv

9. Энергетические состояния в квантовой механике

В приближении Борна–Оппенгеймера
при этом
Е Ee Ev Er ,
e v r
Энергия электронов в поле неподвижных ядер определяется уравнением
H e e Ee e
Энергия колебательного движения определяется уравнением
H v v Ev v
или
[T v Ee ( R1 ... Rn ) Ee ( R1e ... Rne )] Ev v
Энергии вращательных состояний определяются из
H r r Er r