Осесимметричный изгиб оболочек

1.

.
D
.
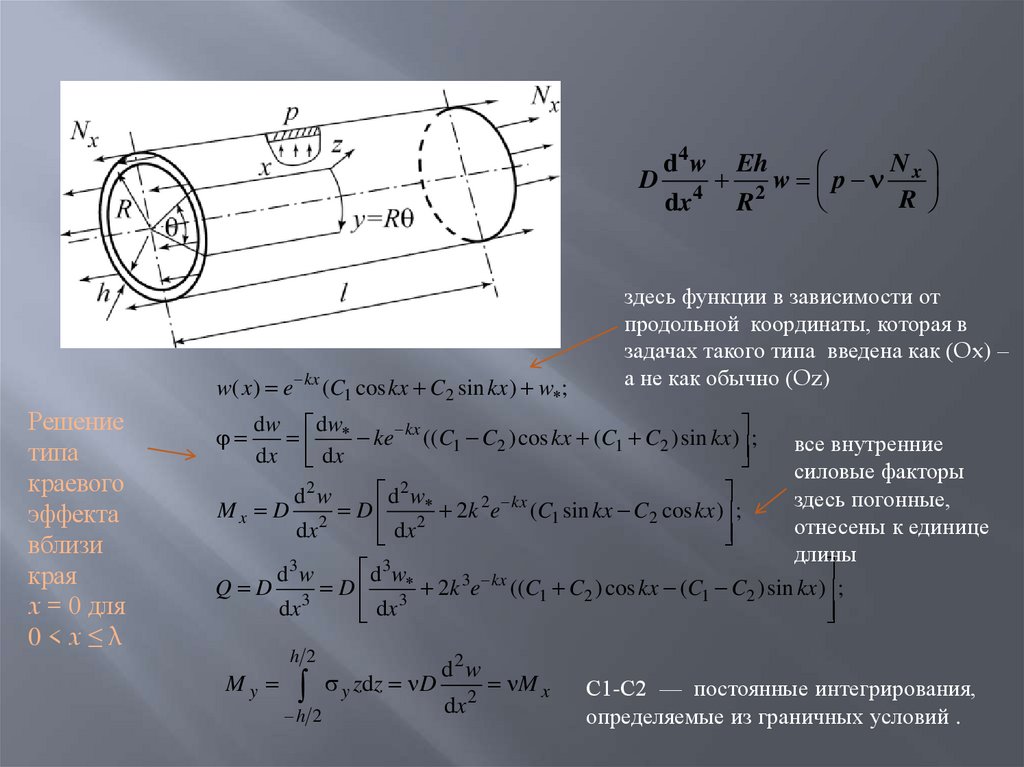
w( x ) e kx (C1 cos kx C2 sin kx ) w ;
Решение
типа
краевого
эффекта
вблизи
края
x = 0 для
0<x≤λ
d4 w
dx
4
Nx
w
p
R
R2
Eh
здесь функции в зависимости от
продольной координаты, которая в
задачах такого типа введена как (Ox) –
а не как обычно (Oz)
dw dw
ke kx ((C1 C2 ) cos kx (C1 C2 )sin kx ) ;
dx dx
все внутренние
силовые факторы
2
2
d w
d w
здесь погонные,
M x D 2 D 2 2k 2 e kx (C1 sin kx C2 cos kx ) ;
отнесены к единице
dx
dx
длины
3
3
d w
d w
Q D 3 D 3 2k 3e kx ((C1 C2 ) cos kx (C1 C2 )sin kx ) ;
dx
dx
h2
My
d2w
y zdz D dx 2 M x
h 2
С1-С2 — постоянные интегрирования,
определяемые из граничных условий .

2.

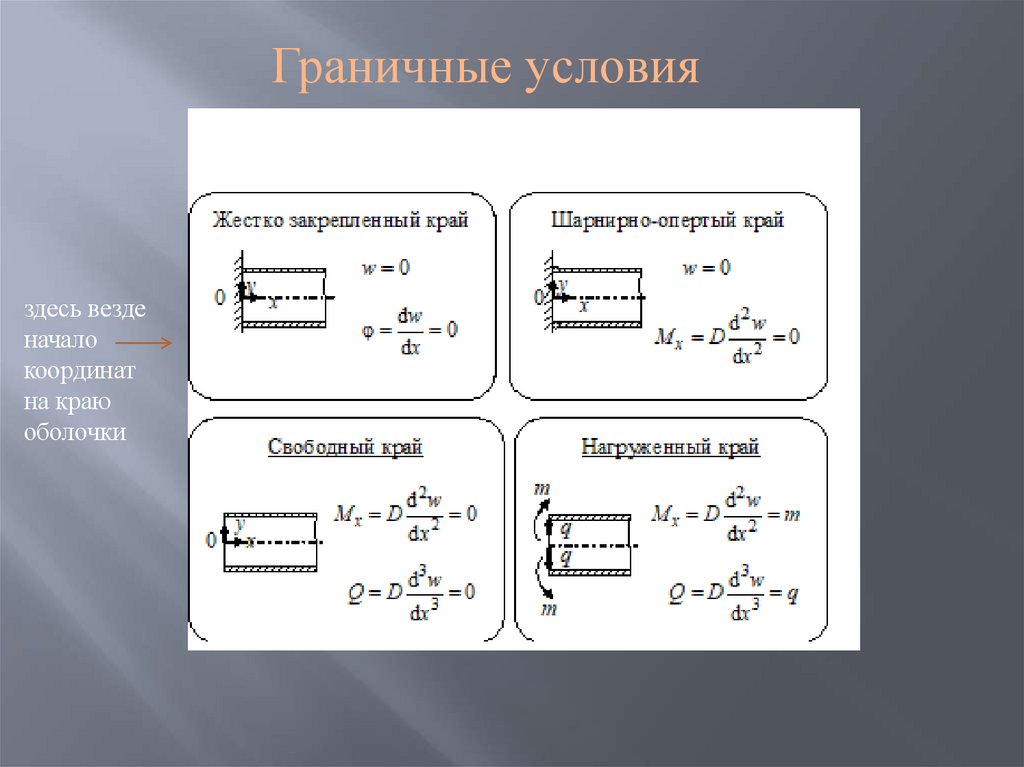
Граничные условия
здесь везде
начало
координат
на краю
оболочки

3.

Пример симметричного
нагружения.
Начало координат помещаем
в точке нагружения (по оси
симметрии).
Известно, что функции
прогиба и момента
симметричны, а функции
угла поворота сечения и
поперечной силы
кососимметричны (будут
равны нулю при
симметричном нагружении).

4.

Пример
кососимметричного
нагружения.
Начало координат помещаем в
точке нагружения (по оси
симметрии).
Известно, что функции
прогиба и момента
симметричны (будут равны
нулю при кососимметричном
наружении), а функции угла
поворота сечения и
поперечной силы
кососимметричны.

5.

Очень интересная задача.
Здесь конструкция
бесконечной оболочки не
является симметричной, т.к.
толщина стенок разная.
Частное решение будет тоже
различным для правой и
левой части.
Таким образом, вместо
граничных условий здесь
используются условия
непрерывности (условия
стыковки) прогиба, угла
поворота, момента и силы в
точке изменения толщин
х=0.
Находим четыре константы
для решения этой задачи.