Похожие презентации:
Оболочки вращения
1. Оболочки вращения
2.
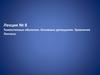
БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК ВРАЩЕНИЯГеометрические соотношения
Срединная поверхность оболочки
вращения получается в результате
вращения плоской кривой
относительно оси, лежащей в
плоскости этой кривой. Такая кривая
называется меридианом. Меридианы
являются линиями главной кривизны
и их принимают в качестве
координатных линий.
Параллели — окружности, образованные пересечением срединной поверхности
оболочки с плоскостями, перпендикулярными ее оси, — представляют семейство
других координатных линий. В качестве криволинейных координат, отсчитываемых
вдоль меридианов и параллелей, возьмем углы α и β: α — угол, который нормаль
образует с осью оболочки, β — угол, отсчитываемый вдоль параллели от
некоторой заданной меридиональной плоскости
Первый главный радиус кривизны поверхности вращения R1 равен радиусу
кривизны меридиана. Второй главный радиус R2 равен отрезку нормали к
поверхности до оси вращения, т. е. согласно рисунку
r
R2
где r — радиус параллели.
sin
3.
Радиусы R1 и R2 не являютсянезависимыми. Действительно, из
рисунка следует, что, с одной
стороны, dsα=R1∙dα, а с другой —
dsα=dr/cosα, т.e. R1∙cosα∙dα=dr.
Подставляя сюда dr, получим:
dr d R2 sin
R1 cos
d
d
Формула для линейного элемента поверхности вращения имеет вид:
ds 2 ds 2 ds 2 R12 d 2 r 2 d 2
т.е.
A R1 , B r
Осевая координата х связана с углом α следующим соотношением
dx ds sin R1 sin d
4.
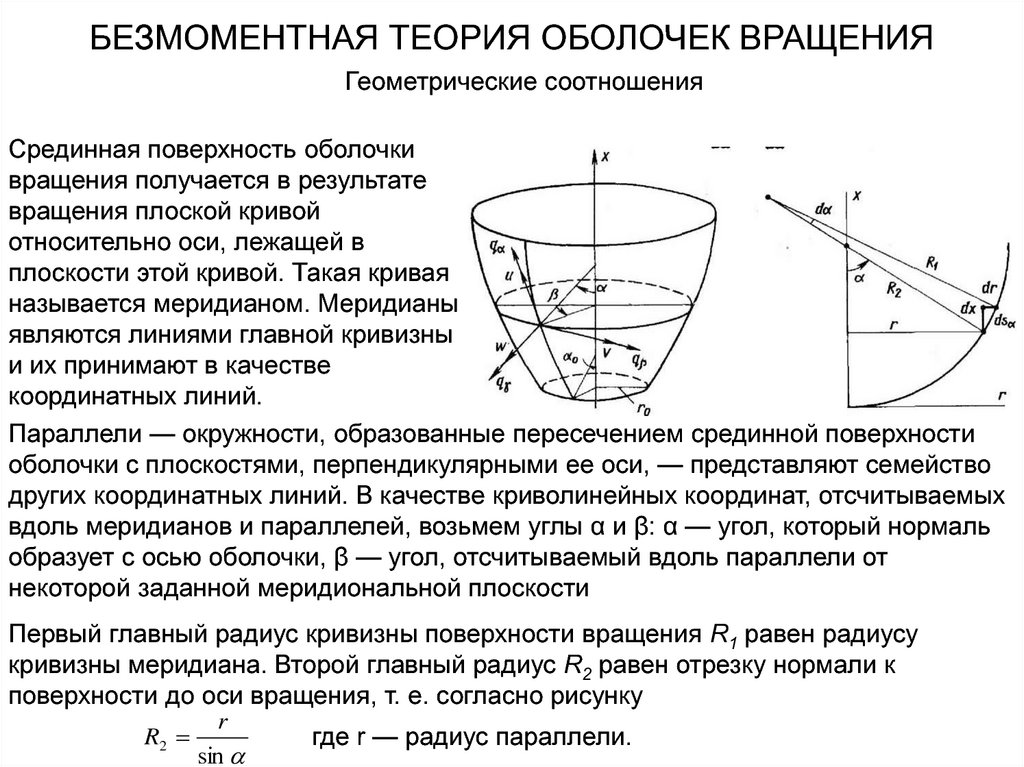
Основные соотношения безмоментной теории оболочекУравнения безмоментной теории могут
быть получены из общих уравнений
теории оболочек, если принять, что
изгибная жесткость оболочки D=0. Однако,
учитывая практическую важность
безмоментной теории, эти уравнения
выводятся традиционным путем в
результате непосредственного анализа
равновесия и геометрии деформирования
оболочки.
Итак, рассмотрим тонкую оболочку
вращения, считая, что она находится в
безмоментном напряженном состоянии.
Выделим бесконечно малый элемент оболочки, находящийся под действием
безмоментных усилий Να, Νβ, Ναβ и заданной поверхностной нагрузки с
компонентами qα, qβ, qγ, направленными вдоль координатных линий α, β и
нормали. Составим уравнения равновесия, т. е. приравняем нулю суммы проекций
сил, действующих на элемент. В направлении касательной к меридиану получим:
N
N
r
N r d N d r
d d N R1 d N d R1 d
N R1 d cos d q R1 r d d 0;
5.
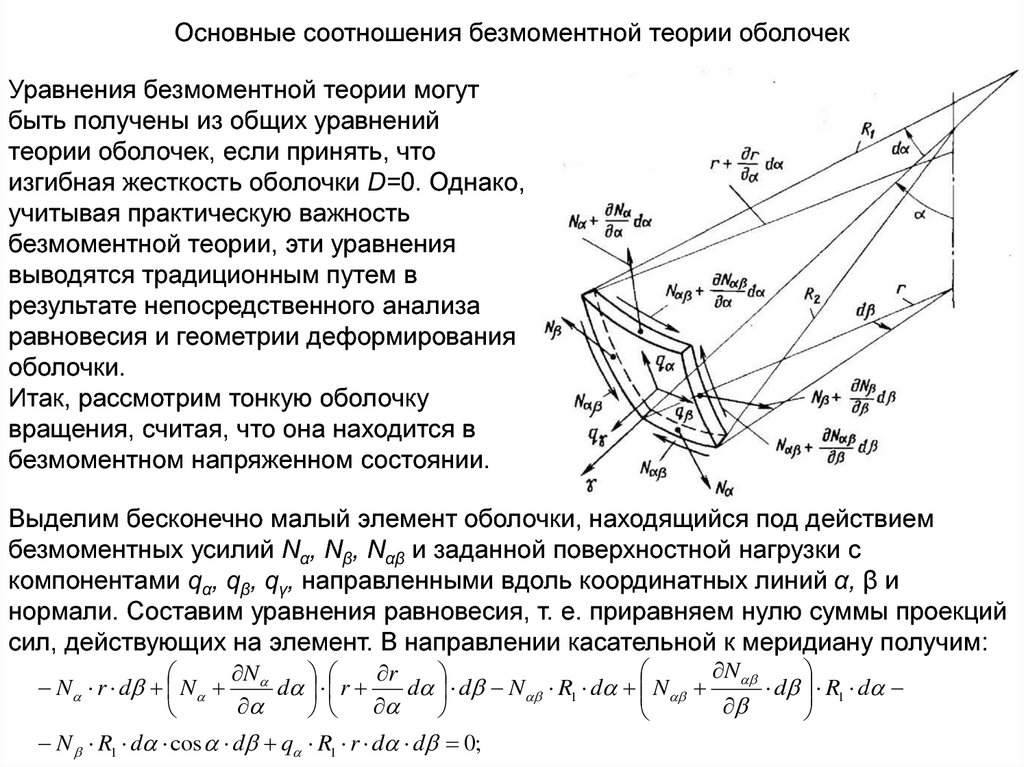
в направлении касательной к параллели:N
r
N r d N d r
d d
N
N R1 d N d R1 d
N R1 d cos d q R1 r d d 0;
В обоих этих уравнениях появление
предпоследних членов обусловлено
наличием малого угла cosα∙dβ между
боковыми гранями элементов.
Сумма проекций действующих сил на нормаль к поверхности:
N r d d N R1 d sin d q R1 r d d 0
где учитывается угол между усилиями Nα на нижней и верхней гранях, равный
π-dα, и угол между усилиями Nβ на боковых гранях, равный π — sinα∙dβ.
6.
В результате уравнения равновесия оболочки вращения при безмоментномнапряженном состоянии записываются в виде:
r N N
R1 N R1 cos q R1 r 0,
r N N
R1 N R1 cos q R1 r 0,
N N
q
R1
R2
Примечательно, что безмоментное напряженное состояние оболочки является
локально статически определимым. Однако в целом для оболочки задача может
оказаться статически неопределимой, если для определения произвольных
функций интегрирования или произвольных констант потребуется использовать
геометрические граничные условия.
7.
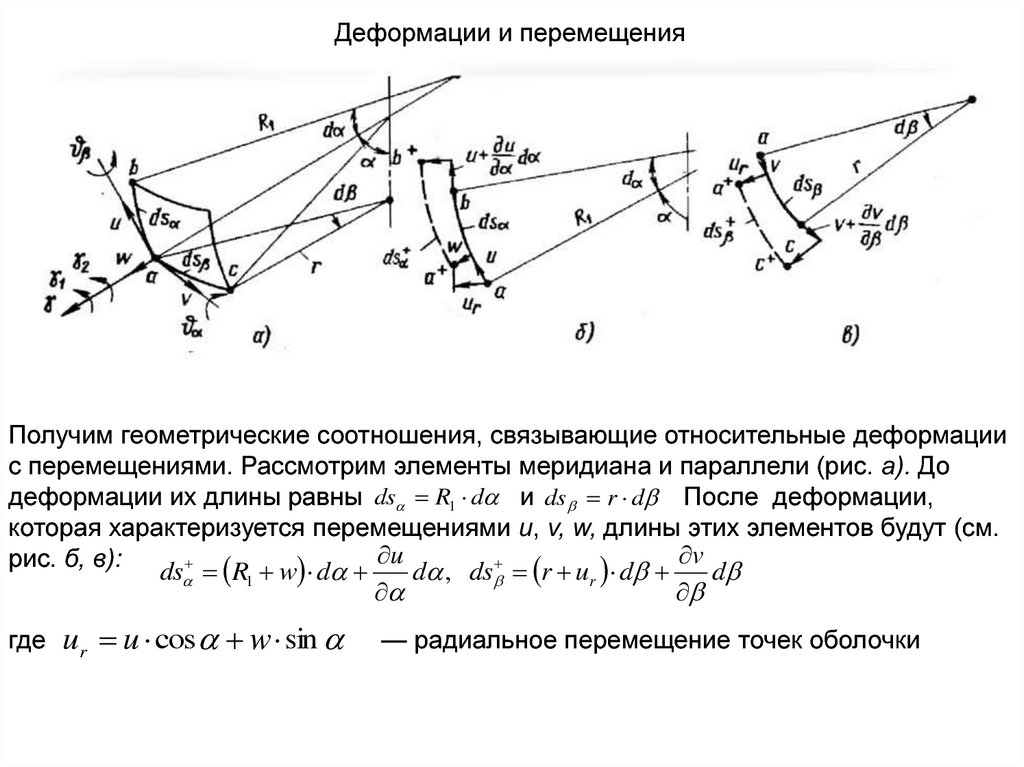
Деформации и перемещенияПолучим геометрические соотношения, связывающие относительные деформации
с перемещениями. Рассмотрим элементы меридиана и параллели (рис. а). До
деформации их длины равны ds R1 d и ds r d После деформации,
которая характеризуется перемещениями u, v, w, длины этих элементов будут (см.
u
v
рис. б, в):
ds R1 w d
d , ds r ur d
d
где
ur u cos w sin
— радиальное перемещение точек оболочки
8.
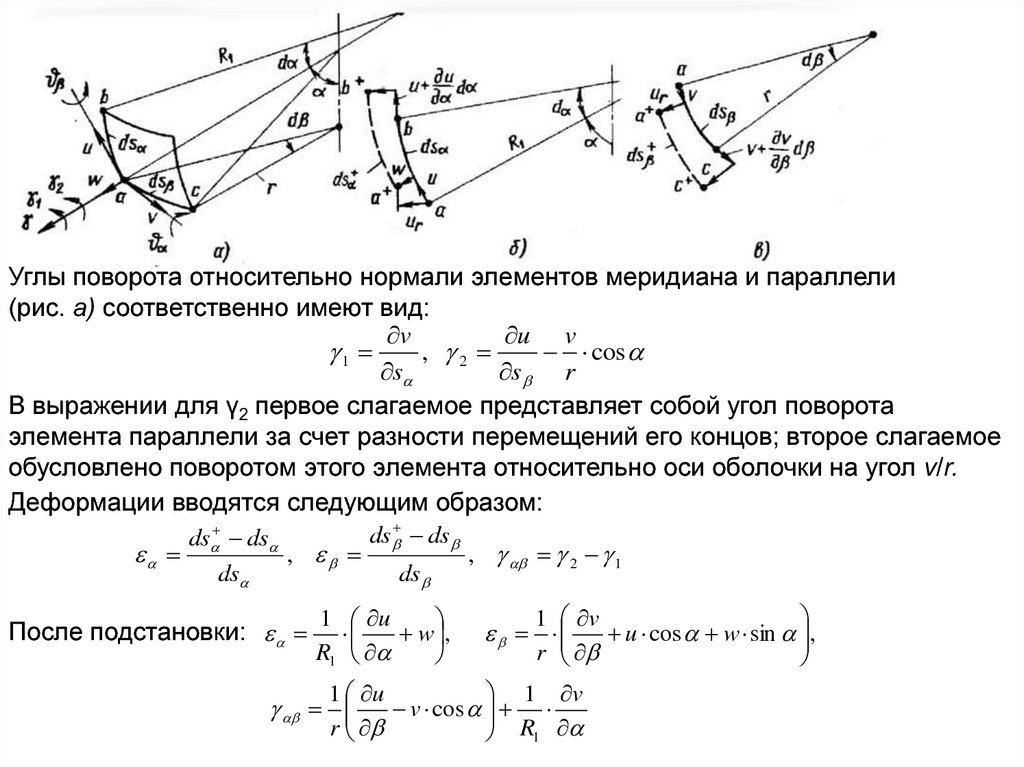
Углы поворота относительно нормали элементов меридиана и параллели(рис. а) соответственно имеют вид:
v
u v
1
, 2
cos
s
s r
В выражении для γ2 первое слагаемое представляет собой угол поворота
элемента параллели за счет разности перемещений его концов; второе слагаемое
обусловлено поворотом этого элемента относительно оси оболочки на угол v/r.
Деформации вводятся следующим образом:
ds ds
ds ds
,
, 2 1
ds
ds
После подстановки:
1 u
w ,
R1
1 u
1 v
u cos w sin ,
r
1
v
v cos
r
R1
9.
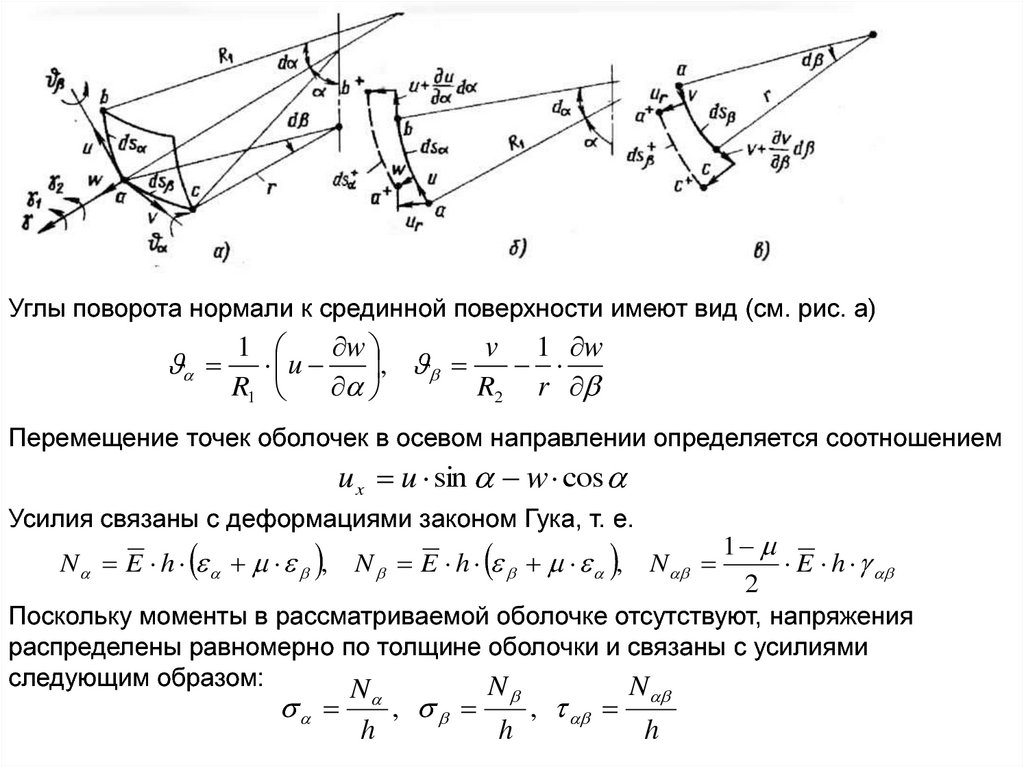
Углы поворота нормали к срединной поверхности имеют вид (см. рис. а)1
R1
w
v 1 w
u
,
R2 r
Перемещение точек оболочек в осевом направлении определяется соотношением
u x u sin w cos
Усилия связаны с деформациями законом Гука, т. е.
1
E h
2
Поскольку моменты в рассматриваемой оболочке отсутствуют, напряжения
распределены равномерно по толщине оболочки и связаны с усилиями
следующим образом:
N
N
N
N E h ,
N E h ,
h
,
h
,
N
h
10.
Полученные соотношения являются основными уравнениями безмоментнойтеории оболочек вращения. Девять уравнений включают столько же неизвестных
— три усилия Nα, Nβ, Nαβ, три деформации εα, εβ, γαβ и три перемещения и, v и w.
Уравнения равновесия могут быть проинтегрированы независимо от остальных, по
найденным из них усилиям с могут быть определены деформации и в результате
интегрирования геометрических соотношений — перемещения. На практике
вместо перемещений и и w часто используются радиальное и осевое перемещения
иr и ux которые выражаются через и и v.
11.
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧКИВРАЩЕНИЯ
Одним из наиболее распространенных случаев нагружения оболочек вращения
является осесимметричное нагружение, при котором поверхностные и краевые
силы не зависят от окружной координаты β и qβ=0. При этом в оболочке вращения
отсутствует окружное перемещение v, а и и w так же, как и ненулевые силовые
факторы Nα, Nβ, Qα, Mα, Mβ, зависят только от переменной α. В условиях
осесимметричного нагружения работают баки, баллоны давления, резервуары и т.
д. Метод расчета таких оболочек строится по аналогии с решением для
цилиндрической оболочки, т. е. напряженное состояние разделяется на
безмоментное и изгибный краевой эффект, локализующийся вблизи краев. Такое
разделение для оболочки вращения произвольной формы является
приближенным, однако для удлиненных в осевом направлении оболочек оно
позволяет построить решение, обладающее приемлемой для практических
расчетов точностью.
12.
Безмоментное напряженное состояниеОсновная система уравнений безмоментной теории оболочек для случая
осесимметричной деформации принимает следующий вид:
r N N R1 cos q R1 r 0,
N N
p,
R1
R2
1
1
u w , u cos w sin ,
R1
r
N E h , N E h
Радиальное и осевое перемещения определяются
u r u cos w sin , u x u sin w cos
угол поворота нормали к срединной поверхности
1
u w
R1
В уравнениях принято qα = q, qγ = р, ( )' обозначает производную по α.
13.
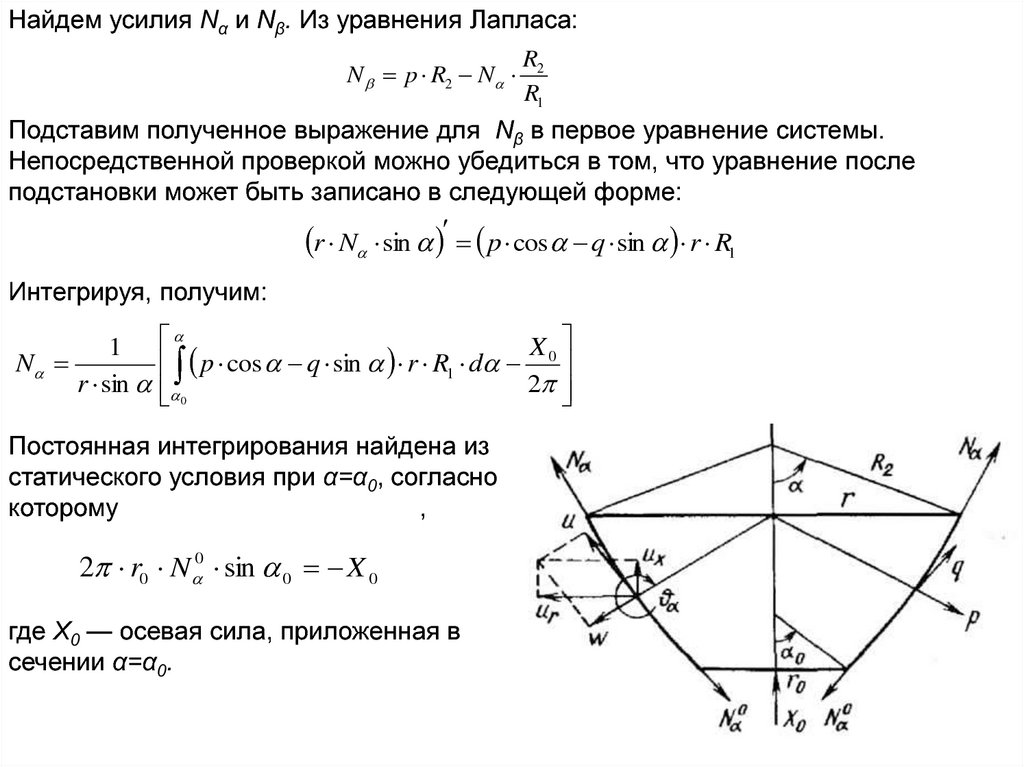
Найдем усилия Nα и Νβ. Из уравнения Лапласа:N p R2 N
R2
R1
Подставим полученное выражение для Νβ в первое уравнение системы.
Непосредственной проверкой можно убедиться в том, что уравнение после
подстановки может быть записано в следующей форме:
r N sin p cos q sin r R1
Интегрируя, получим:
1
N
r sin
X0
p cos q sin r R1 d
2
0
Постоянная интегрирования найдена из
статического условия при α=α0, согласно
которому
,
2 r0 N 0 sin 0 X 0
где Х0 — осевая сила, приложенная в
сечении α=α0.
14.
Наиболее распространенным случаем осесимметричного нагружения являетсявоздействие равномерного внутреннего давления. Полагая в полученных
зависимостях q=0, р=const и учитывая, что R1 cos d dr получим:
r 2 r02 X 0
1
N
p
r sin
2
2
Для замкнутой в вершине оболочки r0=0. При отсутствии осевой силы(Х0=0) из
равенств окончательно будем иметь
p R2
p R2
R2
N
, N
2
2
2
R1
Формулы определяют усилия в замкнутых баллонах давления. В частности, для
цилиндрической части баллона R1 , R2 R и N p R 2 ; для сферического
баллона R1 R2 R и N N p R 2 .
Деформации безмоментной оболочки вращения определяются из закона Гука
1
1
N N ,
N N
E h
E h
Для определения перемещений воспользуемся геометрическими соотношениями
системы уравнений. Из второго соотношения с учетом R2 r sin имеем
w R2 u ctg
15.
Подставляя выражение для w в третье выражение системы, получимu u ctg f R1 где f
Решение этого уравнения имеет вид:
f
R1 d
где F
sin
R2
R1
u F C0 sin
С0 — произвольная постоянная.
Из выражений для u и w получим:
w cos F C0 R2
Радиальное и осевое перемещения, а также угол поворота согласно имеют вид:
ur r,
u x C 0 F u r ctg ,
1
R1
f ctg R2
16.
Для оболочки постоянной толщины выражение для угла поворота преобразуется квиду:
cos
R2
R2
R2
R2 dp
2
p
1
ctg
q
R
E h
R
d
R
sin
1
1
1
1
R2 R2 d 1
1
N
2 2
R1 R1 d R1
R1 R2
Постоянная С0 определяется из геометрического
граничного условия на закрепленном крае
оболочки, которое в соответствии с
безмоментной теорией может быть задано
только для тангенциального перемещения и.
Если безмоментная оболочка вращения в виде пояса закреплена по
тангенциальным смещениям на обоих торцах (рис. а), то в этом случае продольная
реакция на одном из торцов, например на нижнем Х0, является статически
неопределимой и определяется совместно с константой С0 из заданных
геометрических граничных условий
u x x 0 . u x x l 0
Если сила Х0 задана (см. рис. б), постоянная С0 определяется из условия u x x l 0.
В случае, когда оболочка является незакрепленной, например баллон под
действием внутреннего давления, константа С0 является неопределенной — она
представляет перемещение оболочки вдоль оси как недеформируемого твердого
тела.
17.
Безмоментное решение является точным только в определенных случаях.Обычно же оно используется как приближенное решение на большей части
поверхности оболочки вращения при осесимметричном нагружении, если радиус
r(α) и нагрузки q(α), р(α) являются достаточно плавными функциями.
18.
КРАЕВОЙ ЭФФЕКТ В ОБОЛОЧКАХ ВРАЩЕНИЯНа краях оболочки, где она сопрягается с другими оболочками вращения,
круговыми шпангоутами или нагружается осесимметричными нагрузками,
граничные условия на практике редко соответствуют безмоментным условиям.
Поэтому вблизи таких краев оболочка обычно подвергается изгибу.
Дифференциальные уравнения изгиба произвольной оболочки вращения при
осесимметричном нагружении имеют переменные коэффициенты и их точные
решения могут быть получены только в некоторых частных случаях в специальных
функциях (например, для сферы и конуса).
В случае тонких непологих оболочек при плавном изменении радиуса и нагрузок q,
р изгиб в основном происходит вблизи края и по мере удаления от края
напряженное состояние приближается к безмоментному. Поэтому безмоментное
решение приближенно используется в качестве частного решения неоднородной
задач, и по аналогии с w0 в решении для цилиндрической оболочки. При этом
однородное решение, описывающее изгиб оболочки, имеет характер затухающего
краевого эффекта типа wK .
Для простоты и краткости изложения краевой эффект для тонкой непологой
оболочки вращения рассмотрим на основе упрощающих допущений, которые
примем, опираясь на аналогию с краевым эффектом для рассмотренной ранее
цилиндрической оболочки.
19.
Общее решение вблизи края оболочки представляется в виде суммыбезмоментного решения (обозначаем его верхним индексом «0») и однородного
решения в виде краевого эффекта (с индексом «к»):
u u 0 u K , w w0 w K , N N 0 N K , N N 0 N K ,
M M K , M M K , Q Q K
В изгибных силовых факторах M , M , Q естественно, фигурируют только
составляющие краевого эффекта.
При описании краевого эффекта в качестве координаты будем рассматривать
расстояние s, отсчитываемое от края оболочки вдоль меридиана. Вместо угла α
введем угол ψ, отсчитываемый от края, при этом ds = R1∙dψ.
Введение координаты s и угла ψ вместо sα и α позволяет
одинаковым образом описать краевой эффект как на
нижнем, так и на верхнем краях, причем на нижнем крае
ds=dsα, ψ=α, а на верхнем крае ds=-dsα, ψ=π-α.
Оболочку в районе рассматриваемого края будем
считать непологой, если |ctg ψ|<3.
20.
У тонкой непологой оболочки зонакраевого эффекта является достаточно
узкой, и поэтому изменением радиусов
кривизны оболочки и угла ψ в пределах
этой зоны можно пренебрегать, принимая
их значения равными значениям на крае.
В случае оболочки типа пояса, имеющей
два края, краевые эффекты на этих краях
будем рассматривать независимо как
затухающие, считая, что ширина зоны
каждого из них меньше расстояния между
краями вдоль меридиана.
Получим уравнения равновесия. Выделим элемент оболочки, показанный на
рисунке. Составим уравнения проекций сил в направлении нормали и моментов
относительно касательной к верхней грани элемента, выделенного из оболочки в
зоне краевого эффекта:
K dQ K
dr
Q
r ds d Q K r d N K r d d N K ds sin d 0,
ds
ds
ds
K dM K
dr
M
r ds d M K r d M K ds cos d Q K r ds d 0
ds
ds
ds
0
0
Здесь внешние нагрузки q, р и безмоментные усилия N , N , не учитываются, так
как они находятся в равновесии.
21.
Разделив уравнения на r∙dβ∙ds и учитывая, что ds = R1∙dψ получимdr ds cos
K
dQ K
N K N
K ctg
Q
0
ds
R2
R1
R2
r R2 sin ,
dM K
ctg
M K M K
Q K 0
ds
R2
Из уравнения равновесия отсеченной части оболочки,
учитывая, что внешняя нагрузка уравновешивается
усилиями Ν0α, найдем
Q K sin N K cos 0
откуда
N K Q K ctg
В случае непологой оболочки (|ctgψ|< 3) из полученной зависимости следует, что
ΝKα и QKα являются величинами одного порядка. Поперечная сила на основании
второго уравнения равновесия выражается через изгибающие моменты, в
результате чего она зависит от изгибной жесткости оболочки D, пропорциональной
h3. Напомним, что толщина h считается малой. Поэтому для тонких оболочек
усилия ΝKα, так же как и QKα, можно считать пренебрежимо малым по сравнению с
ΝKβ, которое пропорционально h.
22.
Кроме того, при изгибе края достаточно гладкой, тонкой, непологой оболочкиможно предположить, что тангенциальное перемещение uK является
пренебрежимо малым по сравнению с нормальным перемещением wK. На
основании этого примем следующие допущения: N K N K , wK u K 0
Определим угол поворота в плоскости меридиана и изменения главных кривизн
при изгибной деформации оболочки:
dw K
,
ds
1
1 d K d d K
d 2 wK
K
,
R1 R1
ds
ds
ds
ds 2
K
1
1 sin K sin sin K cos sin
dw K ctg
K ctg
R2 R2
r ur
r
r
r
R2
ds
R2
K
где R+1, R+2 — радиусы кривизн деформированной срединной поверхности
оболочки с учетом поворота нормали на малый угол ϑKα. Изменением этих
радиусов за счет деформаций удлинения срединной поверхности пренебрегаем.
23.
Введем весьма существенное для теории краевого эффекта допущение,вытекающее из быстрой изменяемости решения по переменной s. Из выражения
w w0 wK w0 e k C1 cos k C2 sin k
следует, что для цилиндрической оболочки составляющая wK пропорциональна e-kα,
т. е. при дифференцировании по α она умножается на -k. Если k велико, то можно
утверждать, что функции, описывающие краевой эффект, при дифференцировании
существенно возрастают по абсолютной величине, т. е. в уравнениях краевого
эффекта можно пренебречь низшими производными по сравнению с высшими. Из
K
K
этого, в частности, следуёт, что согласно полученным зависимостям
и общие соотношения между моментами и изменениями кривизн
M D ,
M D
можно приближенно записать с учетом полученных выше зависимостей в виде
d 2 wK
d 2 wK
K
K
K
K
K
M D D
, M M D D
2
ds
ds 2
Выведем теперь уравнение краевого эффекта. В соответствии с принятыми выше
K
K
допущениями N N в первом уравнении равновесия пренебрегаем членами,
K
K
содержащимиQ и N при этом считаем, что у непологой оболочки ctgψ не
является большой величиной, а радиус R1 не является малым по сравнению с
радиусом R2.
24.
KdM
ctg
ВО втором уравнении равновесия
M K M K
Q K 0
ds
R2
пренебрегаем вторым членом, содержащим M K и M K M K по сравнению с
первым членом, представляющим производную от быстроизменяющейся функции.
Тогда с учетом полученных выражений для моментов из второго уравнения
равновесия будем иметь
dM K
d 3 wK
K
Q
D
ds
ds 3
K
K
N
dQ K
N
ctg
Q K
0
а из первого уравнения равновесия
ds
R2
R1
R2
с учетом указанных выше допущений получим
K
d 4 wK N
D
0
ds 4
R2
Запишем выражения для окружной деформации εKβ. Из равенств
1
1
и
N N с учетом принятых
u cos w sin
E h
r
допущений и формулы R2 r sin имеем
N K
1
wK
1
K
K
К
K
K
u ctg w
,
N N
R2
R2
E h
E h
К
Приравнивая получим
N K
E h K
w
R2
25.
Kd 4 wK N
0
Подставляя полученное выражение в D
4
ds
R2
4 K
d w
4
K
4
k
w
0 где k 4 E h 4 D R22 3 1 2
получим
4
ds
R
2
2
h2
Здесь радиус R2 в пределах зоны краевого эффекта можно считать постоянным и
равным его значению на рассматриваемом крае. Отметим, что полученное
линейное ДУ аналогично однородному уравнению, соответствующему уравнению
для цилиндрической оболочки. Затухающая часть решения аналогична
выражению для затухающей части цилиндрической оболочки, т. е.
wK e k s C1 cos ks C2 sin ks
Используя дифференциальные зависимости находим
dw K
k e k s C1 cos ks sin ks C2 cos ks sin ks ,
ds
d 2 wK
K
M D
2 D k 2 e k s C1 sin ks C2 cos ks ,
2
ds
d 3wK
K
3
k s
Q D
2
D
k
e
C1 cos ks sin ks C2 cos ks sin ks
3
ds
E h K
M K M K , N K ctg Q K , N K
w .
R2
К
26.
KK
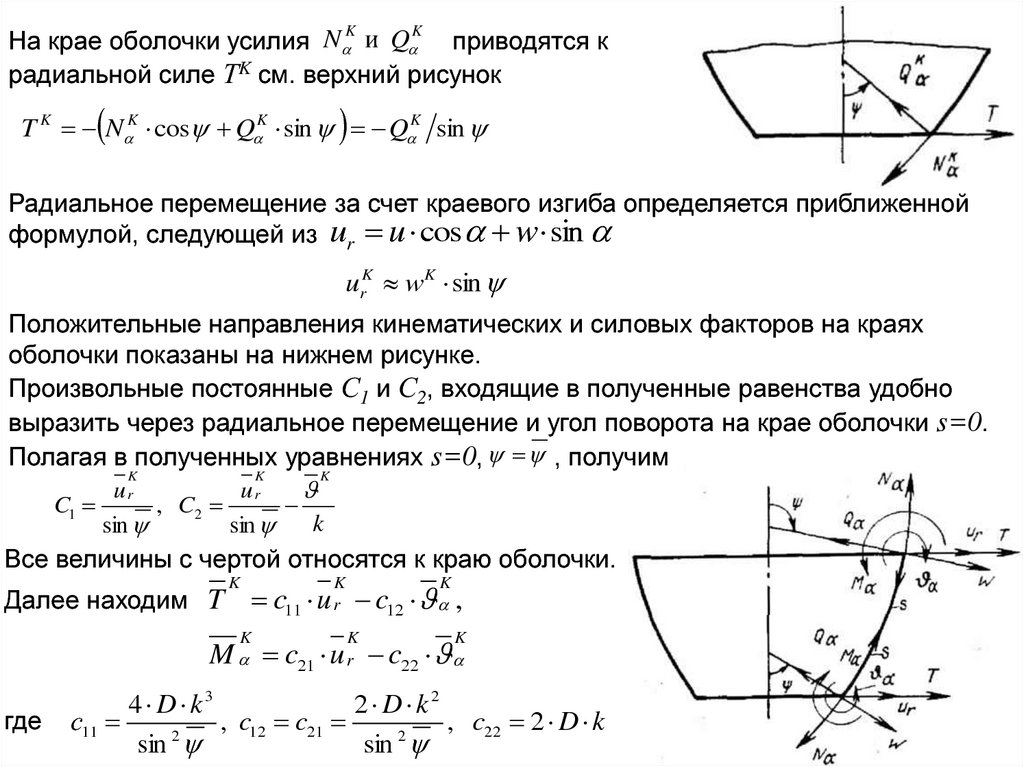
На крае оболочки усилия N и Q приводятся к
радиальной силе ТK см. верхний рисунок
T K N K cos Q K sin Q K sin
Радиальное перемещение за счет краевого изгиба определяется приближенной
формулой, следующей из ur u cos w sin
urK wK sin
Положительные направления кинематических и силовых факторов на краях
оболочки показаны на нижнем рисунке.
Произвольные постоянные С1 и С2, входящие в полученные равенства удобно
выразить через радиальное перемещение и угол поворота на крае оболочки s=0.
Полагая в полученных уравнениях s=0, , получим
K
K
K
ur
ur
C1
, C2
k
sin
sin
Все величины с чертой относятся к краю оболочки.
Далее находим T
K
K
K
c11 u r c12 ,
K
K
r
K
M c21 u c22
где
4 D k3
2 D k2
с11
, c12 c21
, c22 2 D k
2
2
sin
sin
27.
Коэффициенты cij (i, j = 1, 2) называются коэффициентами жесткости краяоболочки. Для безмоментной оболочки D=0, cij=0,
Погрешность формул, полученных на основе приближенного решения для
краевого эффекта, зависит от величины R2 h tg и не превышает 5 %, если на
рассматриваемом крае R2 h tg 5 .
В случае цилиндрической оболочки (ψ=π/2) полученные формулы являются
точными. Практически для тонких оболочек (R2/h>100) построенным приближенным
решением можно пользоваться при значениях краевого угла ψ в пределах
20°<ψ<160°. Ширина зоны краевого эффекта примерно равна π/k, что при μ=0,3
составляет 2,5 R2 h .
28.
ГРАНИЧНЫЕ УСЛОВИЯ И УСЛОВИЯ СОПРЯЖЕНИЯОбщее решение задачи об осесимметричной деформации оболочки
вращения записывается в виде суммы безмоментного решения и краевого
эффекта. Оно содержит три произвольные постоянные С0, С1, С2, которые
должны быть определены из граничных условий или условий сопряжения
на крае оболочки. В качестве граничных условий на крае должны быть
заданы две компоненты перемещений и угол поворота в меридиональной
плоскости или соответствующие имраспределенные силы и момент,
например, u или Nα, w или Qα, ϑα или Mα.
Приведем основные типы граничных условий: жесткое защемление –
u=w=ϑα=0; шарнирное закрепление – u=w=Mα=0, при этом вместо условий
u=w=0 можно использовать условия ur=ux=0.
Условия жесткого соединения оболочек по краям записываются в виде
трех геометрических условий совместности перемещений и углов
поворота и трех статических условий, на основании которых реакции (две
силы и момент) на соединяемых краях должны быть равны по величине и
противоположны по направлению.
29.
,Вслучае, если оболочки
соединяются через упругий
шпангоут, то статические
условия записываются в виде
уравнений равновесия
соединительного шпангоута
под действием сил и
моментов, в число которых
включаются реакции со
стороны оболочек Nα, Т и М.
Реакции T и M можно выразить через радиальное перемещение ur и угол
поворота края оболочки по формулам, аналогичным полученным в
предыдущем вопросе. Суммарные величины ur и складываются из слагаемых,
K
K
представляющих безмоментное решение u r0 , 0 и краевой эффект ur , .
ur ur0 urK
0 K
Значения ur0 , 0 определяются по формулам безмоментного решения, полученным
1
ранее
ur0 r , 0 f ctg R2
R1
В формулах за положительное направление принимается направление от края
оболочки. В связи с тем, что оно совпадает с координатой sα, соответствующей
безмоментному решению только для нижнего края, во втором равенстве для
нижнего края следует принять знак «+», а для верхнего края — знак «-».
30.
ur ur0ur ur0 0
В результате для полных реакций получим: C1
, C2
sin
sin
k
0
0
0
0
T c11 u r u r c12 , M c21 u r u r c22
Здесь cij определяется равенствами, полученными при рассмотрении краевого
эффекта,
4 D k3
2 D k2
с11
sin
2
, c12 c21
sin
2
, c22 2 D k
знак «—» при соответствует нижнему, а знак «+» — верхнему краю оболочки.
Радиальное перемещение ur и угол поворота на крае оболочки, связанной со
шпангоутом, исходя из геометрических условий сопряжения выражают через
радиальное перемещение в центре тяжести поперечного сечения шпангоута wш и
угол поворота этого сечения ш . В итоге при любом числе сопрягаемых со
шпангоутом оболочек, если они являются статически определимыми относительно
безмоментных усилий N 0 , задача сводится к двум линейным алгебраическим
уравнениям относительного wш, ϑш. После их определения находятся ur , и
константы C1, C2 для каждой из сопрягаемых оболочек.
Для определения константы С0 ,входящей в уравнения безмоментного состояния
ставится граничное условие или условие сопряжения для осевого перемещения uх,
которое равно
u x C0 F ur ctg
где ur ur0 urK – полное радиальное перемещение.
31.
Запишем условия сопряжения длясистемы двух оболочек, соединенных
через упругий шпангоут, который
свободно оперт по контуру радиуса r0 .
(см. рис) Будем считать, что на
опорном контуре вертикальное
смещение равно нулю, т. е. u0=0.
Распределенную вертикальную силу
Р0 находим из уравнения равновесия
всей системы. Затем для каждой из
оболочек 1 и 2 записываются решения по безмоментной теории и теории краевого
эффекта. Геометрические условия жесткого сопряжения оболочек со шпангоутом
имеют вид: u 0, u b b , u b b , , ,
0
x ,1
ш
0
1
x,2
ш
0
2
,1
ш
,2
ш
ur ,1 wш ш a1 , ur , 2 wш ш a2
Уравнения равновесия радиальных сил и моментов, действующих на шпангоут,
записываются в форме
Eш Fш
r1
r2
w
T
T
T0 ,
ш
1
2
Rш2
Rш
Rш
Eш I ш
r1
r2
M
T
a
M
T
a
M0
ш
,1
1
1
,2
2
2
Rш2
Rш
Rш
Здесь Fш и Iш — площадь и момент инерции поперечного сечения шпангоута
относительно радиальной оси, проходящей через его центр тяжести; множители в
виде отношения радиусов (r1/Rш и другие) вошли в уравнения в силу того, что
соответствующие распределенные силы и моменты ( T1 и другие) отнесены к
единице длины тех линий, на которых они приложены.
32.
В полученных уравнениях T0 и M 0представляют собой
распределенную радиальную
нагрузку и распределенный
момент, которые возникают за
счет реакций безмоментныx
оболочек (от известных
меридиональных усилий ) и
внешней нагрузки, действующей
не шпангоут. В рассматриваемом
случае имеем:
T0 N 0 1
r1
r
cos 1 N 0 2 2 cos 2 ,
Rш
Rш
M 0 N 0 1
r
r1
r
b1 sin 1 a1 cos 1 N 0 2 2 b2 sin 2 a2 cos 2 P0 ш a0
Rш
Rш
Rш
Уравнение проекций сил в направлении оси оболочки
N Rr
0
1
1
ш
sin 1 N 0 2
r
r2
sin 2 P0 0 0
Rш
Rш
позволяет определить реакцию P0.
33.
Уравнения равновесия с учетом зависимостей для T , M для каждой из оболочек игеометрических соотношений приводятся к виду
B11 wш B12 ш B01,
B21 wш B22 ш B02 .
Коэффициенты уравнений в рассматриваемом случае будут равны
B11 c11 1
E F
r1
r
c11 2 2 ш 2 ш ,
Rш
Rш
Rш
B12 B21 c12 1 c11 1 a1
r1
r
c12 2 c11 2 a1 2 ,
Rш
Rш
E I
r1
r
2
c22
2 c12 2 a2 c11 2 a22 2 ш 2 ш
Rш
Rш
Rш
r
r
B01 c11 1 ur0,1 c12 1 0,1 1 c11 2 ur0, 2 c12 2 0, 2 2 T0 ,
Rш
Rш
1
B22 c22
2 c12 1 a1 c11 1 a12
Rr c c a u
1
B02 c12 1 c11 1 a1 ur0,1 c22
c12 1 a1 0,1
1
ш
2
12
2
11
2
0
r ,2
Rr
2
c22
c12 2 a2 0, 2
2
M0
ш
Здесь B11, B12=B21 и B22 представляют собой коэффициенты жесткости шпангоута с
учетом присоединенных оболочек. Эти коэффициенты легко обобщаются путем
суммирования на случай произвольного числа оболочек (в формулах
коэффициенты жесткости cij различных оболочек отмечаются верхним индексом).
34.
Во многих случаях размеры поперечного сечения шпангоута малы по сравнению сего радиусом. В таких случаях при приближенных расчетах можно пренебречь
всеми эксцентриситетами, положив в полученных уравнениях r=r1=r2=Rш,
a1=a2=b1=b2=0. Шпангоут при таком упрощении по существу рассматривается как
упругая линия в виде окружности радиуса
После решения уравнений для каждой из оболочек определяются константы C1, С2,
и С0.
35.
АНТИСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧКИВРАЩЕНИЯ
Помимо осесимметричного нагружения,
рассмотренного в предыдущих вопросах,
распространенным расчетным случаем
является антисимметричное нагружение,
вызывающее общий изгиб оболочки.
Такое нагружение характерно, например,
для отсеков летательных аппаратов.
Рассмотрим тонкую оболочку вращения
(рис. а), находящуюся под действием
поверхностных нагрузок вида
q q 1 cos , q q 1 sin , p p 1 cos
Пусть распределенные нагрузки (или реакции) на краях оболочки заданы
аналогичным образом, т. е. меридиональные усилия, поперечные усилия и
изгибающие моменты распределены вдоль краев по закону cosβ, а окружные
усилия — по закону sinβ. Все эти нагрузки в каждом поперечном сечении х = const
приводятся к равнодействующей поперечной силе Y и изгибающему моменту L,
вызывающим общий изгиб и сдвиг оболочки как балки (см. рис. б).
36.
Если нагрузки, радиусы кривизны и толщина оболочки изменяются вмеридиональном направлении достаточно плавно, то при антисимметричном
нагружении так же, как и при осесимметричном, оболочка в основном испытывает
безмоментное напряженное состояние. На краях, где оболочка нагружается
распределенными поперечными силами и изгибающими моментами, а также в
местах сопряжения различных оболочек возникает быстро затухающее
моментное напряженное состояние типа краевого эффекта, который изменяется в
окружном направлении пропорционально cosβ.
На основании этого приближенное решение задачи при антисимметричном
нагружении оболочки вращения может быть получено так же, как и при
осесимметричном нагружении, в виде суммы безмоментного решения и
моментного решения в виде краевого эффекта.
37.
БЕЗМОМЕНТНОЕ РЕШЕНИЕ ПРИ АНТИСИММЕТРИЧНОМ НАГРУЖЕНИИПри действии антисимметричных поверхностных нагрузок,
q q 1 cos , q q 1 sin , p p 1 cos
как следует из уравнений равновесия безмоментной оболочки вращения
r N N
R1 N R1 cos q R1 r 0,
r N N
R1 N R1 cos q R1 r 0,
N N
q
R1
R2
распределенные усилия изменяются в окружном направлении следующим
образом:
N N 1 cos , N N 1 cos , N N 1 sin
1
где N 1 , N 1 , N
— неизвестные функции, которые можно определить, интегрируя
уравнения равновесия по α. Однако проще составить уравнения равновесия
отсеченной части оболочки.
38.
Равнодействующая поперечная сила и равнодействующий момент внешнихнагрузок, действующих на отсеченную часть оболочки (см. рис. ), имеют вид:
2
Y Y0 q cos cos q sin p sin cos r d R1 d ,
0 0
2
L L0 Y0 x x0 q sin p cos r 2 cos d R1 d
0 0
2
q cos cos q sin p sin cos r d x x1 R1 d
0 0
где Y0 и L0 — равнодействующие
распределенных нагрузок, приложенных на
нижнем крае оболочки; х — координата
рассматриваемого сечения; x1 — текущая
координата (х0 <х1< х, dx1=R1∙sinα·dα).
Уравнения равновесия отсеченной части
оболочки (рис. б)
2
Y
N cos cos N sin r d 0,
0
2
L N sin r 2 cos d 0
0
Эти уравнения являются интегралами первых двух дифференциальных уравнений
равновесия
39.
Выполняя интегрирование по β с учетом выражений для нагрузок, получим1
Y r N 1 cos N
0,
L r 2 N 1 sin 0.
1
Отсюда определяются амплитудные функции распределенных усилий N 1 и N
Усилие Nβ затем находится из третьего уравнения равновесия
1 N 1
R2 cos
N N cos p
R1
1
Деформации оболочки определяем из закона Гука
1
sin
1 cos , 1 cos ,
где
1
N
1
1
1
1
N 1 N 1 , 1
N 1 N 1 ,
E h
E h
G h
Из геометрических соотношений, связывающих деформации и перемещения в
оболочках вращения, получим
u u1 cos , v v1 sin , w w1 cos ,
du1
w1 R1 1 ,
d
v1
u1 ctg w1 R2 1 ,
sin
R2 dv1 1
u1
1
v ctg
R2
R1 d
sin
Из первого уравнения второй группы выразим w1, подставим w1 во второе
уравнение и поделим его на sinα ; третье уравнение продифференцируем по α. В
результате этих преобразований получим
40.
v11 du 1 cos 1
1
u
R2 1 R1 1 ,
2
2
sin
sin sin d sin
1
d R2 dv1
dv1
v1
1 du 1 cos 1 d R2
ctg
u
d R1 d
d sin 2 sin d sin 2
d
Вычитая из второго уравнения первое, будем иметь
1
1
1
d R2 dv1
dv1 d R2 R2 R1
ctg
d R1 d
d
d
sin
1
d
1
dv1 d R2 R1 R2 1
1
или sin R2
d R1 sin d
d
sin R1
Так как R1·sinα·dα=dx, то последнее уравнение можно записать в виде
d 2 v1
F1
dx 2
1
d R2
1
1
F1
R2 sin
dx
sin 2
где
R
2 1 1
R1
x x
Интегрируя полученное уравнение получим v F1 dx dx A1 x A2
1
0 0
После этого из третьего и первого уравнений геометрических соотношений найдем
x x
x
u R2 sin cos F1 dx dx A1 x A2 r sin F1 dx A1 ,
0 0
0
du 1
1
1
w R1 R1 sin
dx
1
1
41.
Нетрудно заметить, что решения, содержащие произвольные константы А1 и А2,представляют перемещения недеформированной оболочки как твердого тела за
счет поворота на угол А1 и смещения A2 в сечении х=0. Если оболочка закреплена
на крае безмоментным образом (только по тангенциальным перемещениям), то
константы А1 и А2 определяются из условий v1=0, и1=0 на этом крае. В общем
случае, когда условия закрепления или сопряжения не являются безмоментными,
константы А1 и А2 определяются совместно с произвольными константами,
входящими в моментную часть решения.
42.
КРАЕВОЙ ЭФФЕКТ ПРИ АНТИСИММЕТРИЧНОМ НАГРУЖЕНИИПоскольку антисимметричное напряженно-деформированное состояние оболочки
меняется в окружном направлении медленно (по закону cos β), то
антисимметричное (моментное) состояние по характеру его изменения в
меридиональном направлении очень близко к осесимметричному краевому
эффекту. На основании этого в районе края, где при антисимметричной
деформации оболочка испытывает изгиб, приближенное общее решение
представляется в виде суммы безмоментного решения и краевого эффекта, т. е.
u u 1 cos , v v1 sin , w w1 cos w K cos
где wK берется в таком же виде, как и при осесимметричной деформации
w K e ks C1 cos ks C2 sin ks
Дуга s отсчитывается от рассматриваемого края (ds=R1·dψ, ψ=α — на нижнем крае и
ψ=π-α – на верхнем крае).
Изгибающие моменты и усилия в зоне краевого эффекта
M M K cos , M M K cos , Q Q K cos ,
1
N N 1 N K cos , N N 1 N 1 cos , N N
sin
K
K
K
K
где M , Q , N , N определяются по тем же формулам, что и для
осесимметричного нагружения
43.
Произвольные постоянные С1 и С2 определяются совместно с константами А1, A2,входящими в безмоментное решение, из граничных условий на крае. При этом
константы А1, A2 определяются для оболочки в целом, а константы С1 и С2 —только
на рассматриваемом крае. Всего на каждом крае должно быть задано четыре
граничных условия, например, для и или Να, v или Ναβ, w или Qα, ϑα или Μα.
В качестве примера запишем граничные условия
на краях оболочки, жестко закрепленной при х=l
и нагруженной при х=0:
а) тангенциальной сдвигающей нагрузкой q0·sinβ
б) радиальной нагрузкой q0·cosβ (см. рис.).
В обоих случаях эти нагрузки приводятся к одной
и той же равнодействующей силе Y0=π·r0·q0.
Следовательно, вдали от края х=0 напряженные
состояния оболочки будут одинаковыми.
Граничные условия на краях оболочки записываются в виде:
при х=l: и=0, ν=0, w=0, ϑα=0;
при х=0 в случае (a): Nα=0, Nαβ=q0·sinβ, Qα=0, Мα=0
в случае (б): Nα=-q0·cosα0·cosβ, Ναβ=0, Qa= q0·sinα0·cosβ, Mα=0.
В случае «а» напряженное состояние оболочки является безмоментным, за
исключением зоны краевого эффекта вблизи закрепленного края х=l. В случае «б»
возникает также изгибный краевой эффект вблизи края х=0.
44.
При формулировке условий сопряжения оболочек вращения: упругим шпангоутомили друг с другом так же, как и при осесимметричной деформации, вместо
перемещений и, w удобнее рассматривать радиальное и осевое перемещения иr и
их, которые связаны с и и w формулами, полученными в общей теории оболочек
u x u sin w cos
ur u cos w sin
При этом вместо усилий N K и Q K вводится их равнодействующая — радиальное
усилие Тк, которое наряду с моментом Мα выражается через перемещение и угол
поворота на рассматриваемом крае оболочки по формулам
1
1
T c11 u r u r c12 ,
1
1
M c21 u r u r c22
где u r0 и r 0 при антисимметричной деформации заменены на u r1 и r1




































 Механика
Механика