Напряжения и перемещения при изгибе

1. Напряжения и перемещения при изгибе

Нормальные напряжения при изгибе прямого бруса
Рассмотрим балку при чистом изгибе:
Выделим участок балки, где
MZ
MZ 0 ;
QY = 0.
MZ = const
MZ

2. Основные положения

1. При чистом изгибе возникают растянутые и сжатые зоны.
Волокна, находящиеся на границе зон, не испытывают ни
растяжения, ни сжатия. Эти волокна образуют
нейтральный слой.
Сжатая зона
MZ
Нейтральный слой
MZ
Растянутая зона

3. Основные положения (продолжение 1)

2. Справедлива гипотеза плоских сечений. Сечения бруса,
бывшие плоскими и нормальными к его оси до деформации,
остаются плоскими и нормальными к оси бруса после
деформации (Синии сечения).
3. Линия пересечения нейтрального слоя с поперечным
сечением называется нейтральной осью сечения.
Нейтральная ось
слой
Нейтральный слой

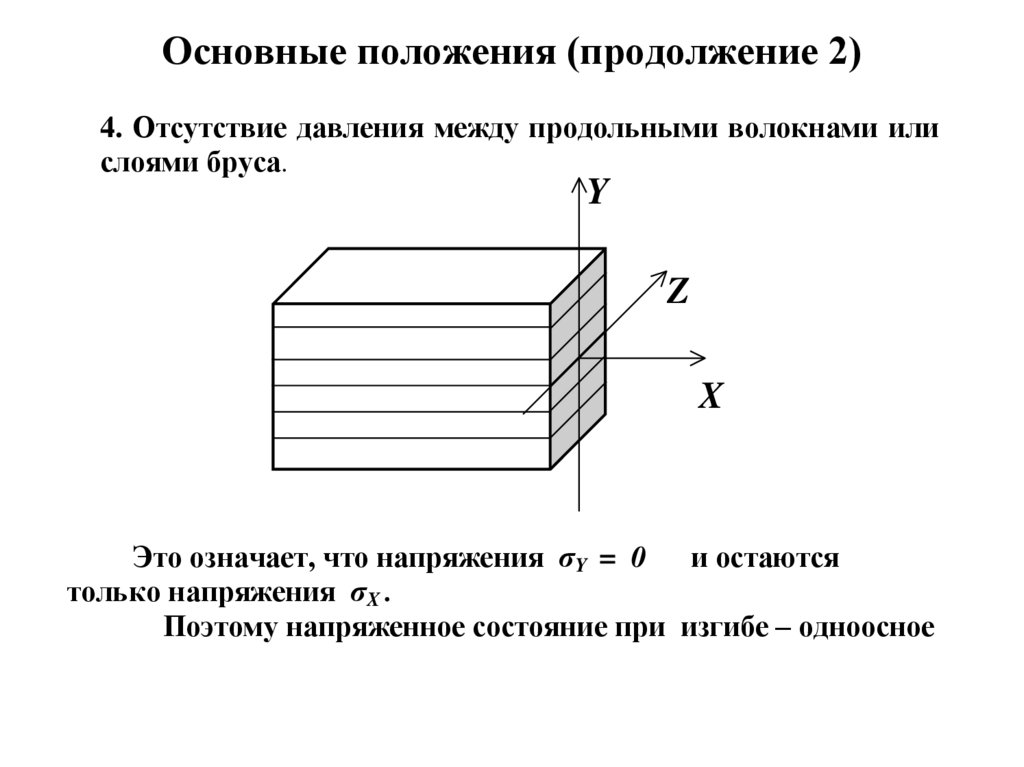
4. Основные положения (продолжение 2)

4. Отсутствие давления между продольными волокнами или
слоями бруса.
Y
Z
X
Это означает, что напряжения σY = 0 и остаются
только напряжения σX .
Поэтому напряженное состояние при изгибе – одноосное

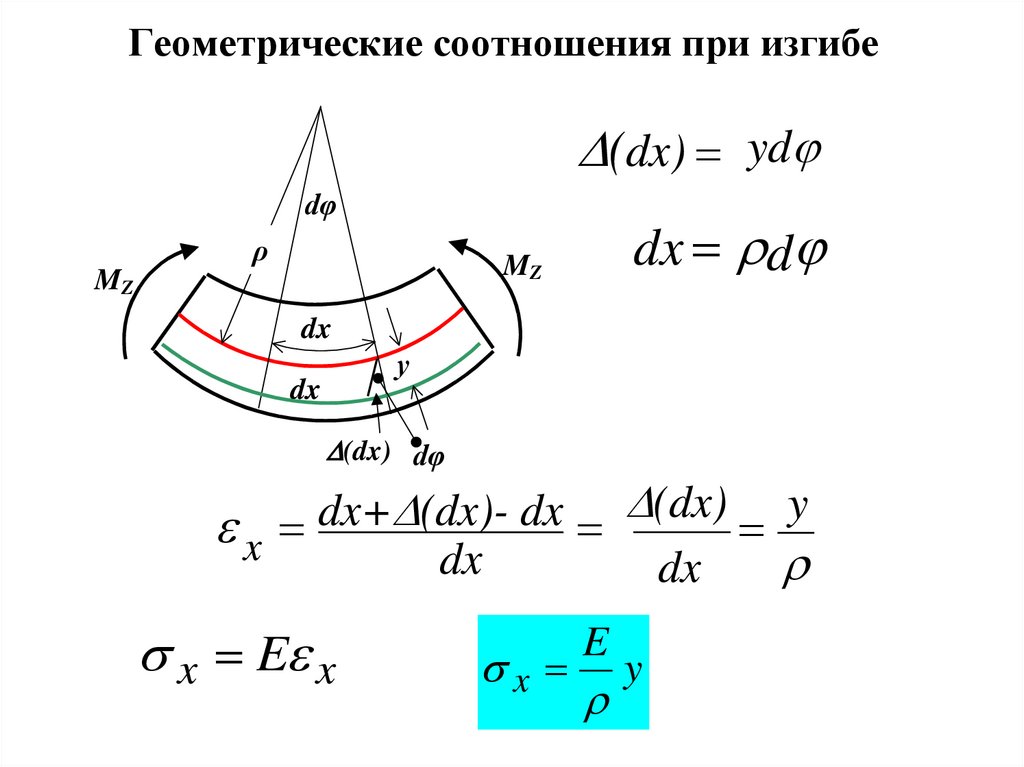
5. Геометрические соотношения при изгибе

D(dx) ydj
dφ
ρ
dx dj
MZ
MZ
dx
у
dx
D(dx) dφ
D(dx) y
dx+
D
(dx)dx
x
dx
dx
x E x
x
E
y

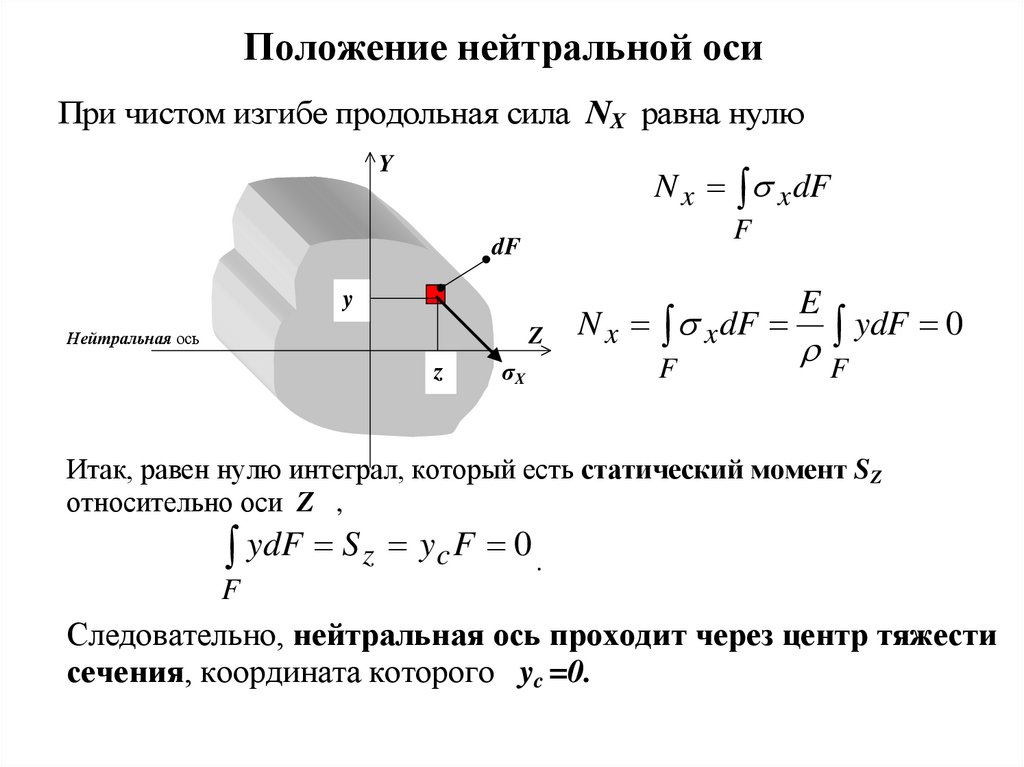
6. Положение нейтральной оси

При чистом изгибе продольная сила NX равна нулю
Y
N x x dF
F
dF
y
Z
Нейтральная ось
z
σX
N x x dF
F
E
ydF 0
F
Итак, равен нулю интеграл, который есть статический момент SZ
относительно оси Z ,
ydF S z yc F 0 .
F
Следовательно, нейтральная ось проходит через центр тяжести
сечения, координата которого yc =0.

7. Выбор системы координат

Поместим начало координат в центр тяжести сечения С.
Y
dF
y
Z
Нейтральная ось
С
z
σX
M y x zdF
F
E
yzdF 0
F
Поэтому равен нулю интеграл, который есть центробежный
момент инерции IYZ ,
yzdF I yz 0 .
F
А это означает, что оси Y и Z есть главные центральные
оси сечения.

8. Напряжения и относительные деформации

Подсчитаем теперь изгибающий момент MZ ,
создаваемый напряжениями σx.
M z x ydF
F
Mz
Iz
E
E
2
y dF
F
E
Iz
Mz
x y
y
Iz
E
I z y 2 dF
F
Mz
x
y
EI z
Итак, и напряжения, и относительные деформации при изгибе
являются линейной функцией координаты Y точки сечения.

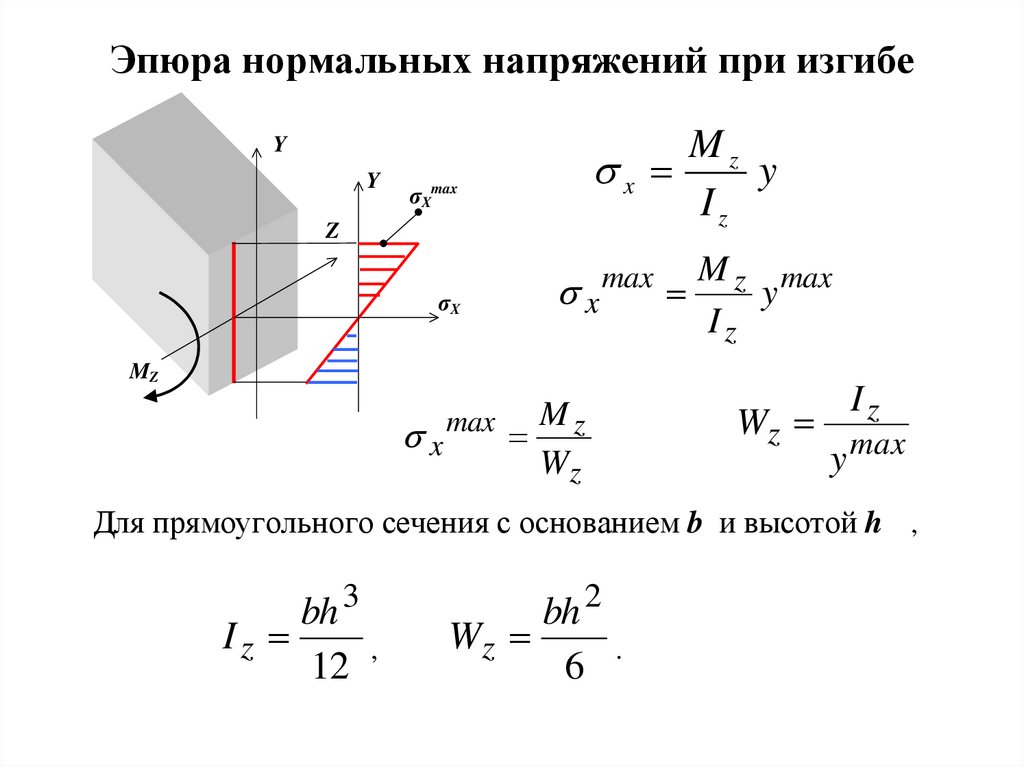
9. Эпюра нормальных напряжений при изгибе

Mz
x
y
Iz
Y
Y
σXmax
Z
σX
x
max
M z max
y
Iz
MZ
x
max
Mz
Wz
Wz
Iz
y max
Для прямоугольного сечения с основанием b и высотой h ,
bh 3
Iz
,
12
bh 2
Wz
.
6

10. Нормальные напряжения при поперечном изгибе

При поперечном изгибе не равны нулю и MZ , и QY .
При наличии поперечной силы гипотеза плоских сечений,
строго говоря, не оправдывается.
Однако, если отношение высоты h балки к ее длине L
h
1 ,
L
то искажение сечений мало и гипотеза плоских сечений выполняется с
большой степенью точности и для нормальных напряжений справедлива
формула
Mz
x
y
Iz

11. Касательные напряжения при поперечном изгибе (допущения)

1. Рассматривается балка, имеющая высокое прямоугольное поперечное
сечение, т.е.
h>
2.
b
2. Касательные напряжения направлены параллельно вызываю щей их
силе,
tXY
QY .
3. Касательные напряжения не изменяются по ширине сечения, т.е. они
не зависят от координаты Z,
t XY (Y const) const
4. Касательные нап ряжения зависят только от координаты Y.

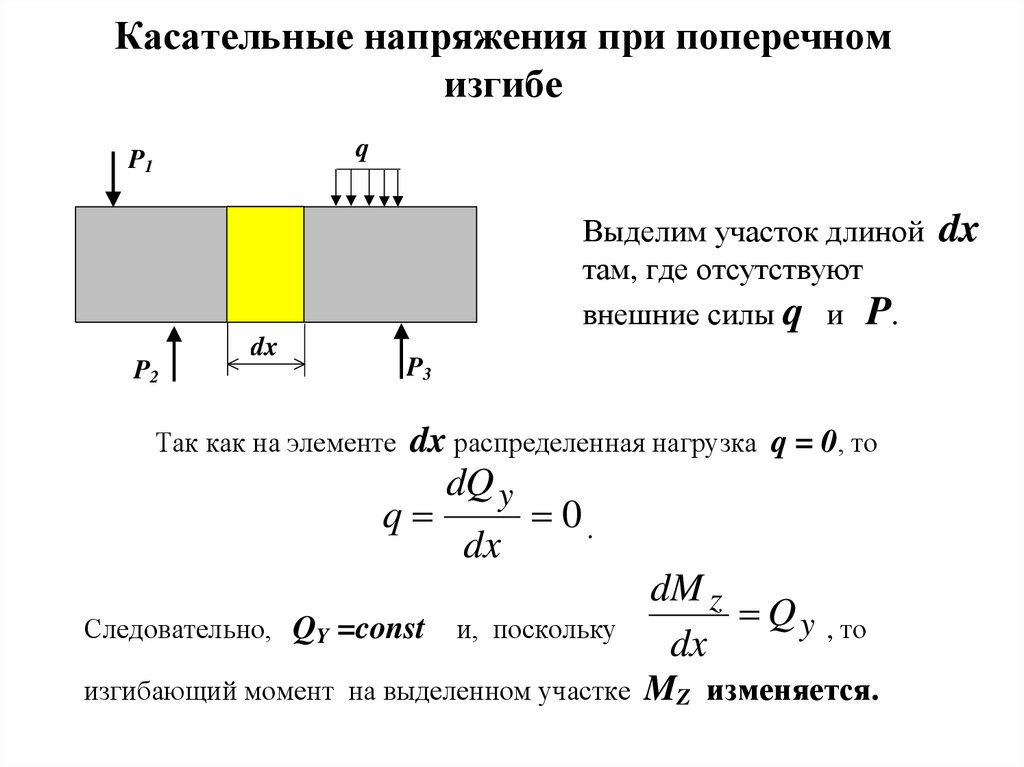
12. Касательные напряжения при поперечном изгибе

q
P1
Выделим участок длиной dx
там, где отсутствуют
внешние силы q и P.
P2
dx
P3
Так как на элементе dx распределенная нагрузка q = 0, то
q
Следовательно, QY =const
dQ y
dx
0.
и, поскольку
dM z
Q y , то
dx
изгибающий момент на выделенном участке MZ изменяется.

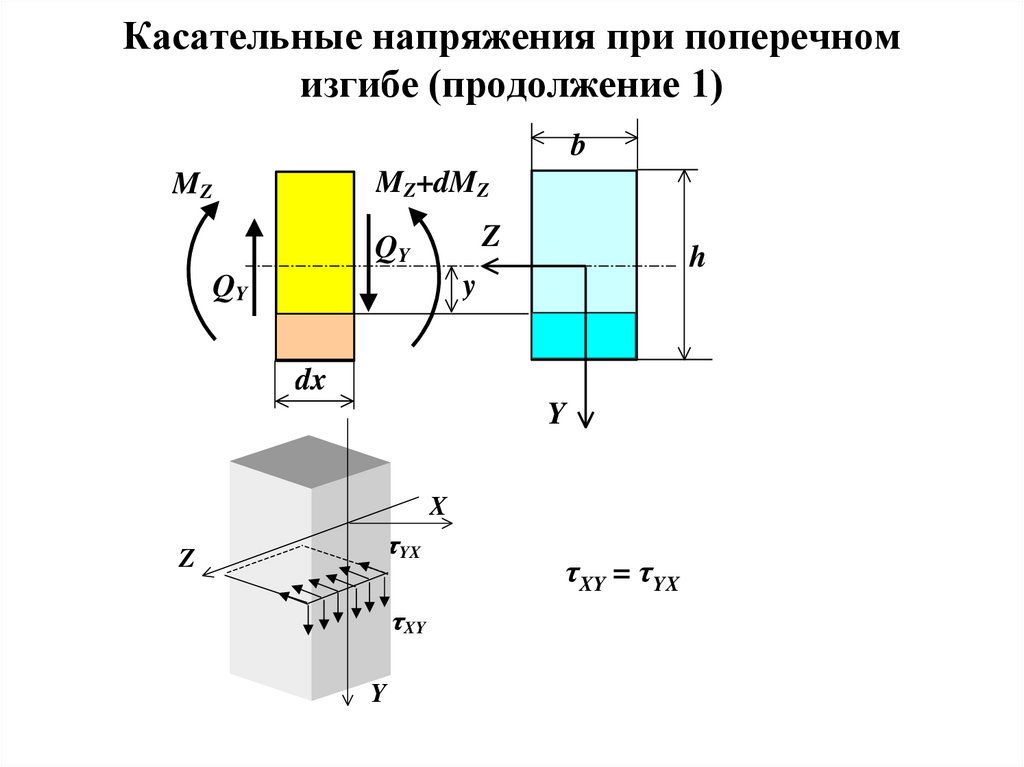
13. Касательные напряжения при поперечном изгибе (продолжение 1)

b
MZ+dMZ
MZ
Z
QY
h
y
QY
dx
Y
X
τYX
Z
τXY
Y
τXY = τYX

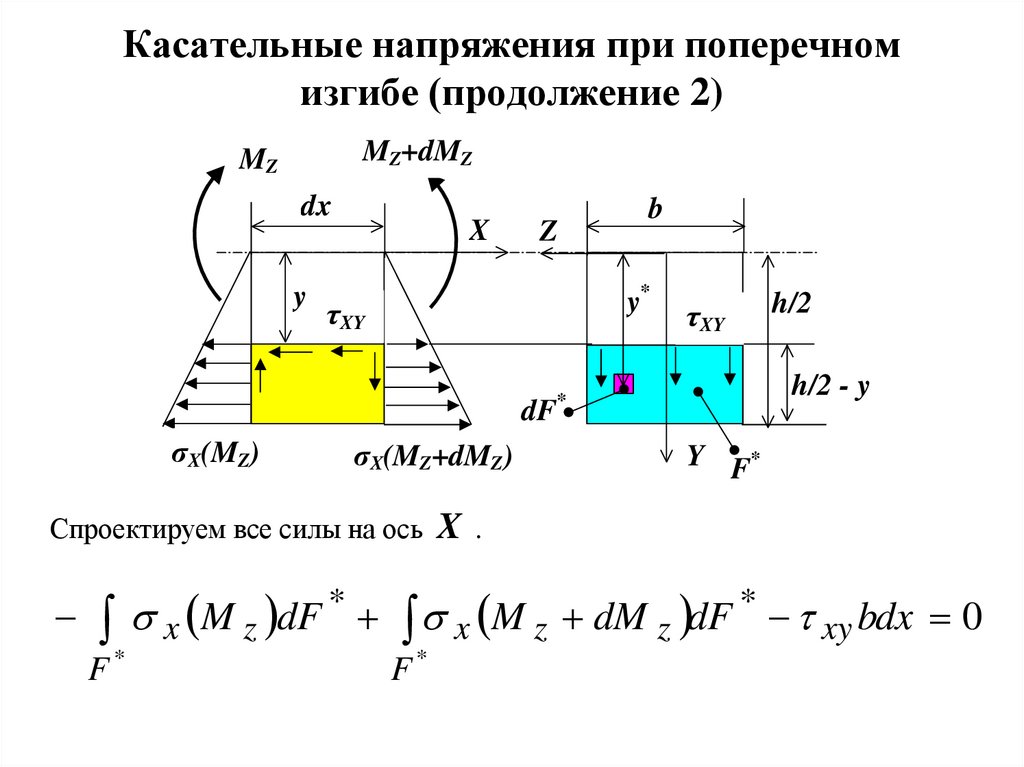
14. Касательные напряжения при поперечном изгибе (продолжение 2)

MZ+dMZ
MZ
dx
y
X
Z
b
y*
τXY
τXY
h/2 - y
*
dF
σX(MZ)
σX(MZ+dMZ)
h/2
Y F*
Спроектируем все силы на ось X .
x ( M z )dF * x ( M z dM z )dF * t xy bdx 0
F*
F*

15. Касательные напряжения при поперечном изгибе – формула Журавского

Mz
x
y , то получаем
Так как
Iz
Mz
* * M z dM z
* *
y
dF
y
dF t xy bdx 0
Iz *
Iz
*
F
F
dM z
* *
y
dF t xy bdx 0
Iz *
F
*
( )
*
*
y
dF
S
y
z
Поскольку интеграл
F
*
, где
y y*
h
2,
dM z
Qy
- статический момент площади F относительно оси Z и
dx
*
( )
то получаем формулу для касательных напряжений при поперечном изгибе
t xy
Q y S z y*
bI z
,
где
( ) F yc
Sz y
*
*
и
bh 3
Iz
12

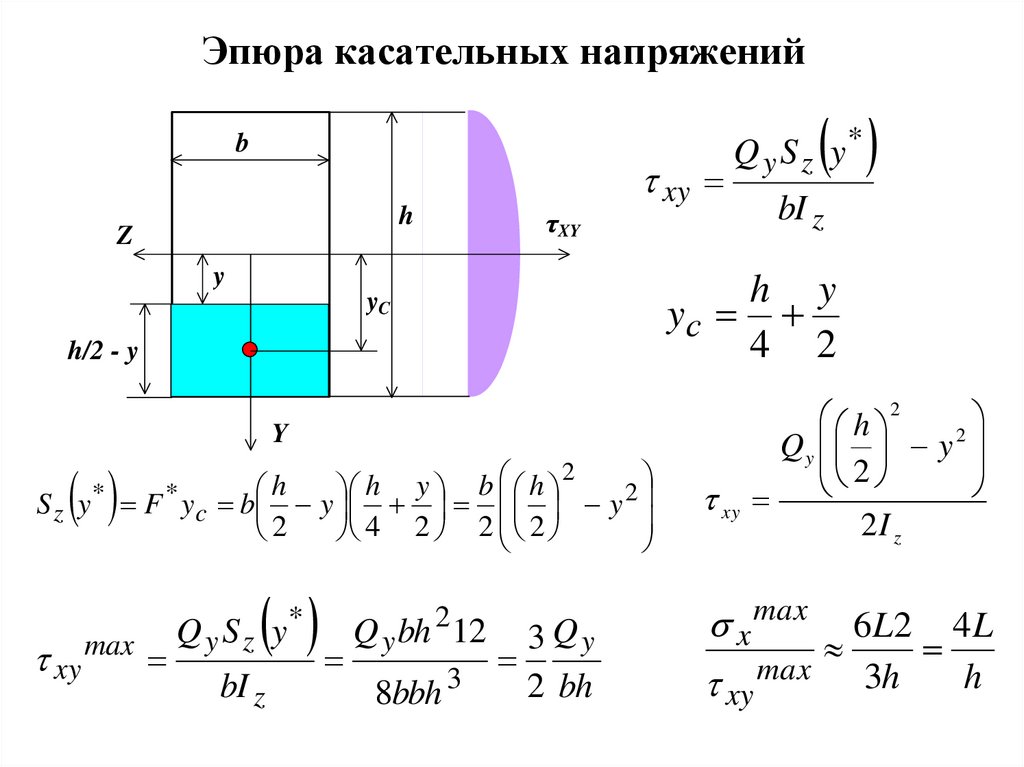
16. Эпюра касательных напряжений

b
t xy
h
Z
τXY
y
h/2 - y
Y
( )
2
h
h y b h
2
S z y F yc b y y
2
4 2 2 2
*
( ) Q y bh 12 3 Q y
*
t xy
max
Qy Sz y
bI z
bI z
h y
yс
4 2
yC
*
( )
Q y S z y*
2
8bbh 3
2 bh
h 2
2
Qy y
2
t xy
2I z
x max
6 L2 4 L
h
t xy max 3h

17. Напряженное состояние при изгибе балки

P
P
σX
τXY
–
Mz
x
y
Iz
Z
+
a
Pa
Y
a
MZ
bI z
3
+
x
QY
P
+
–
-P
t xy
( )
Q y S z y*
x
bh
Iz
12
( )
2
b h
*
2
Sz y y
2 2

18. Расчет на прочность при плоском изгибе

a
σxc
p c
–
ymaxc
b
Для обеспечения прочности
необходимо выполнение
двух условий:
yc
σx
С
Z
p
y
max
a
Z1
b
Y
;
Mz p
y max p
Iz
M
Wp z ;
p
Wp
и xc c .
xp p
+
σxp
Mz c
y max c .
Iz
M
Wc z .
p
ymax
a yc
c
ymax
b yc
c
Iz
p
y max
Wc
Iz
c
ymax

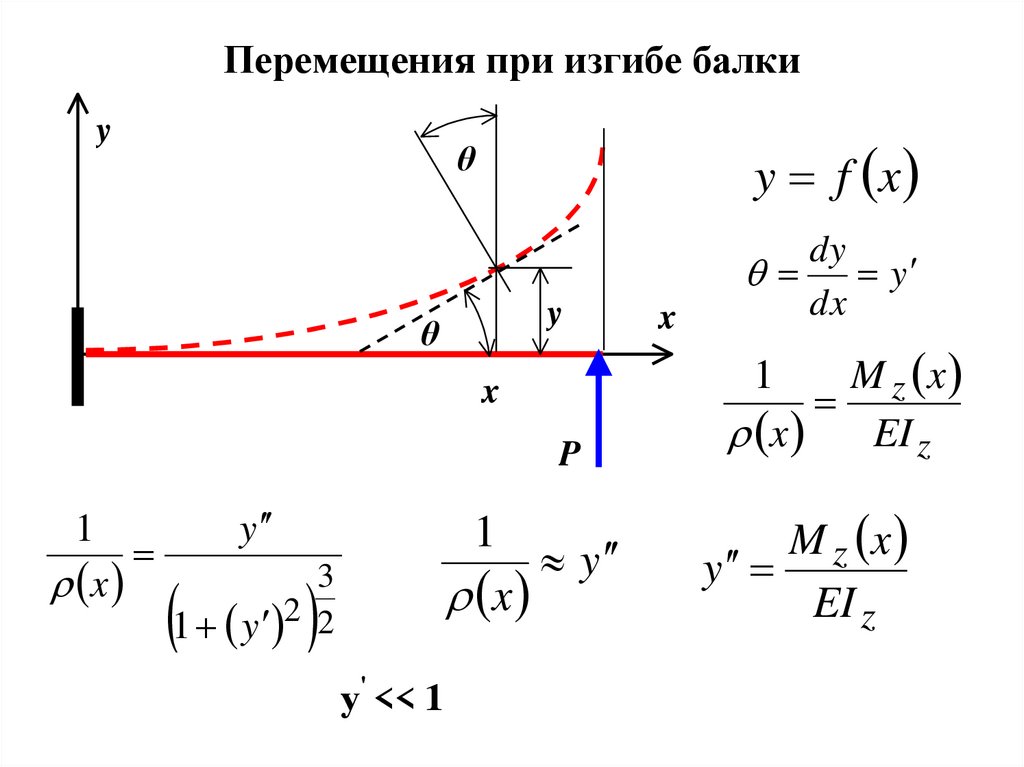
19. Перемещения при изгибе балки

y
y f (x )
θ
y
θ
x
P
1
(x )
y
(
1
y
(x )
)
3
1 ( y )2 2
у' << 1
x
dy
y
dx
M z (x )
1
(x )
EI z
M z (x )
y
EI z

20. Интегрирование уравнения упругой линии балки

M z (x )
y
EI z .
Интегрируем это уравнение.
Угол поворота сечения будет равен
1
y (x )
M z ( x )dx c ,
EI z
прогиб -
1
(
y
M z ( x )dx)dx cx d .
EI z
Постоянные интегрирования c и d находят из условий, налагаемых
опорами на линейные и угловые перемещения.

21. Пример интегрирования уравнения упругой линии балки

M
x
O
A
MZ (x) = M = const
L
Граничные условия – угол поворота и прогиб в заделки равны нулю, т.е.
θ(0) = 0 и y(0) = 0.
Это дает нулевые постоянные интегрирования
c = 0 и d =0.
(x )
(x L )
Mx
EI z
;
Mx 2
y (x )
2 EI z
ML
EI z ;
M L2
;
y (x L )
2 EI z .

22. Пример численного интегрирования уравнения упругой линии балки

q
a
a
a = 1 m ; q = 10 кН/м.
R1
q
R2
R1
0
M z ( x)
a
x
R 1 ( x
a ) if a x 2 a
a
q x
x
if 0 x a
2
q a x
a
2
0 kN m otherwise
3a
2
R2
qa
2

23. Пример численного интегрирования уравнения упругой линии балки (продолжение 1)

E
5
2 10 MPa
100 cm
M z ( x)
dx dx
E I z
C1 a
C2 0 m
M z ( x)
dx dx
E I z
C1 2 a
Given
a
x
0 m
0 m
2 a
x
0 m
C1
C2
0 m
4
Iz
Find ( C1 C2 )
C1 0.017
C2 0 m
C2 14.577 mm

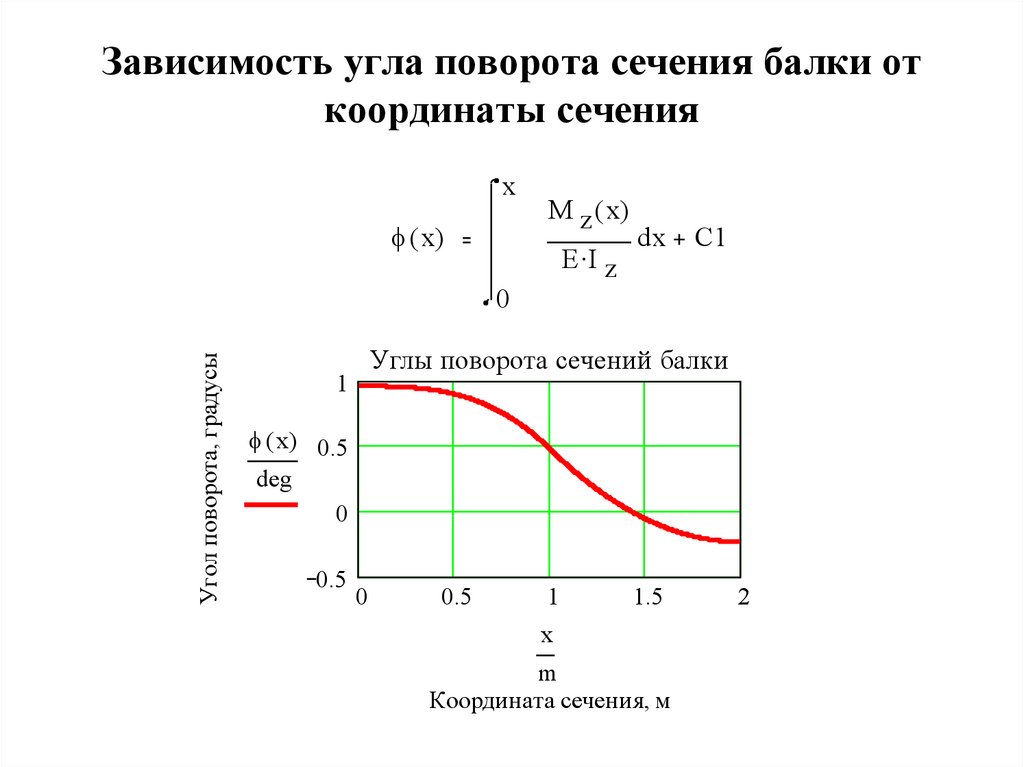
24. Зависимость угла поворота сечения балки от координаты сечения

x
( x)
M z ( x)
dx
EIz
C1
Угол поворота, градусы
0
Углы поворота сечений балки
1
( x) 0.5
deg
0
0.5
0
0.5
1
1.5
x
m
Координата сечения, м
2

25. Зависимость прогиба балки от координаты сечения

x
( x) d x
y ( x)
C2
0
Прогибы балки
Прогиб, мм
10
y( x)
0
mm
10
20
0
0.5
1
1.5
x
m
Координата сечений, м
2