Двойные интегралы

1. Двойные интегралы

Пусть дана функция z=f(x,y) непрерывная и
неотрицательная в области G
Если существует предел
n
f k , k wk , где
0
lim
k 1
f(x,y) – функция, заданная в области G, причем этот
предел не зависит от способа разбиения области G на
частичные области k и выбора точек N k k , k ,
то он называется двойным интегралом от функции
f(x,y) по области G
ОБОЗНАЧЕНИЕ
G
n
f k , k wk
0
f ( x, y )dw lim
k 1

2. Двойные интегралы

f k , k
N k k , k
k
V
G
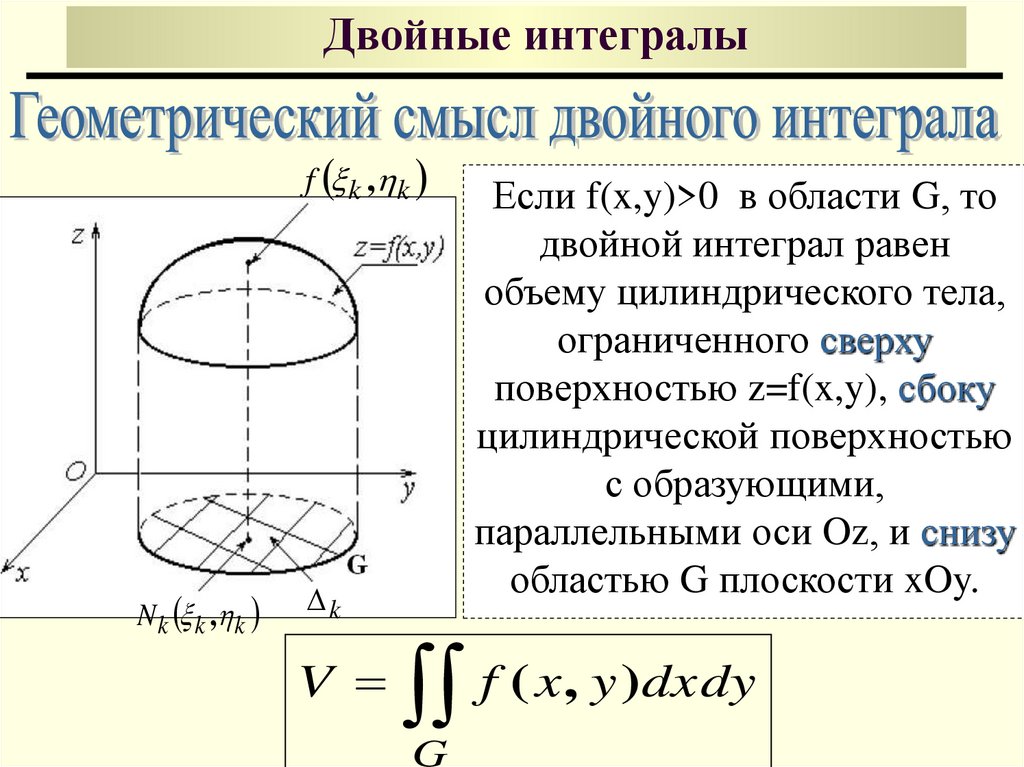
Если f(x,y)>0 в области G, то
двойной интеграл равен
объему цилиндрического тела,
ограниченного сверху
поверхностью z=f(x,y), сбоку
цилиндрической поверхностью
с образующими,
параллельными оси Oz, и снизу
областью G плоскости xOy.
f ( x , y )dxdy

3. Двойные интегралы

Кривая называется гладкой, если в каждой точке
существует касательная и при переходе от точки к точке
положение этой касательной меняется непрерывно
Непрерывная кривая, состоящая из конечного числа
гладких кусков, называется кусочно-гладкой
Если область G с кусочно-гладкой границей Г
ограничена и замкнута, а функция f(x,y) непрерывна в
области G, то эта функция интегрируема в области G.
В дальнейшем будем предполагать, что условия
этой теоремы выполнены

4. Свойства двойного интеграла

1. Постоянный множитель можно вынести за знак
двойного интеграла
2. Двойной интеграл от суммы двух функций равен
сумме двойных интегралов от этих функций
(свойство справедливо для суммы любого конечного
числа функций)
3. Пусть область G разбита на две области G1 и G2
Тогда
G
f ( x, y )dw
G1
f ( x, y )dw
G2
f ( x, y )dw

5. Свойства двойного интеграла

4. Если функция f(x,y)>0 в области G, то
f ( x, y )dw 0
G
5. Теорема о среднем: Двойной интеграл равен
произведению значения подынтегральной функции
в некоторой точке области интегрирования на
площадь этой области
S (G )
G
dxdy

6. Вычисление двойных интегралов

ЗАДАЧА Вычислить двойной интеграл
f ( x, y )dw 0
G
от непрерывной в области G функции f(x,y)
G x, y : a x b, c y d
y
b
d
a
c
d
b
c
a
f ( x, y)dw dx f x, y dy (1)
d
G
G
c
a
b x
f ( x, y)dw dy f x, y dx (2)
G

7. Вычисление двойных интегралов

Выражения в правой части (1) и (2) называются
повторными интегралами.
Для вычисления (1) надо последовательно взять два
обычных определенных
интеграла: сначала
d
внутренний интеграл f x, y dy
, в котором x
c
считается постоянной, а затем полученное выражение
(оно зависит от x) проинтегрировать по x от a до b –
внешний интеграл
Аналогично при втором способе перехода от двойной
интегральной суммы к повторной

8. Пример

x y dw, G x, y : 0 x 1, 0 y 1
2
2
G
0 0
1
1
1
1
1 3
x y dw dx ( x y )dy ( x y y ) dx
3
0
G
2
2
1
2
2
0
1
1
2
1 3 1
( x )dx x x
3
3 0 3
3
0
2
2

9. Вычисление двойных интегралов

G – произвольная область на плоскости XOY
y 2 (x)
D
y
d
x 1( y )
А
c
a
Если y 1(x) и y 2 (x) уравнения нижней и верхней
B
G
частей контура, ограничиваюx 2 ( y)
щего область G, на которые он
C
делится точками А и В. Тогда
x
y 1(x)
G
b
b
2 ( x)
f ( x, y )dw dx
a
f x, y dy
1 ( x )

10. Вычисление двойных интегралов

Если x 1( y ) и x 2 ( y) - уравнения левой и
правой частей контура, ограничивающего область G,
на которые он делится точками С и D. Тогда
G
d
2 ( y)
f ( x, y )dw dy
c
f x, y dx
1( y)

11. Пример

x y dxdy
G
2
y
x
область G ограничена линиями y=x и
y
1
x
0
x2
x
y
dxdy
dx
(
x
y
)
dy
1
y x
y x2
1
x
G
1
x
1
1 2
2 1 2 3 1 4
( xy y ) dx ( x x x x )dx
2
2
2
x2
0
0
1
1 3 1 4 1 5
3
( x x x )
2
4
10 0 20

12. Двойной интеграл в полярных координатах

Связь декартовых и полярных
координат
x r cos
G
f ( x, y )dw
d
r2 ( )
y r sin
f ( r cos , r sin )rdrd
G
f (r cos , r sin )rdr
r1 ( )
Если подынтегральная функция или уравнение границы
области интегрирования содержит сумму x 2 y 2 , то
переходят к двойному интегралу в полярных координатах

13. Пример

x 2 y 2
dxdy
G
область G – первая четверть круга с центром в начале
координат и радиусом, равным 1
x 2 y 2 (r cos )2 (r sin )2 r 2
1
2
2
x y r
1
G
2
1
r
d
dr
2
2
r
2
x y
0
0
dxdy

14. Вычисление площади кривой поверхности

Пусть - участок поверхности z=f(x,y), а область G –
его проекция на координатную плоскость XOY
Предположим, что функция f(x,y) и ее первые частные
производные непрерывны в G вплоть до границы
Площадь S поверхности
вычисляется по формуле
S
G
1 f x 2 ( x, y ) f y 2 ( x, y )dw

15. Пример

Вычислить площадь поверхности сферы
x2 y 2 z 2 R2
Уравнение верхней поверхности сферы z R 2 x 2 y 2
y
x
z y
z x
,
2
2
2
R2 x2 y2
R x y
1 z x 2 z y 2 1
1
S
2
R 2 x2 y 2
R
G
x2 y2
R2 x2 y2
dxdy
R
R2 x2 y2
область интегрирования
определяется условием
x2 y2 R2

16. Пример

S 2
R 2 x 2 y 2
R
2
R2 r 2
dxdy 2 d
G
2
R
2
2
d(R r )
R2 r 2
R d
0
4 R
0
R
0
2
2 R
0
R
rdr
0
R
2
( R 2 r 2 )d 2 R Rd
0
0
2
S 4 R
2
- площадь поверхности сферы