Кратные интегралы (двойные, тройные интегралы)

1.

2.

3.

Ограниченные области
Замкнутые области
Неограниченные области

4.

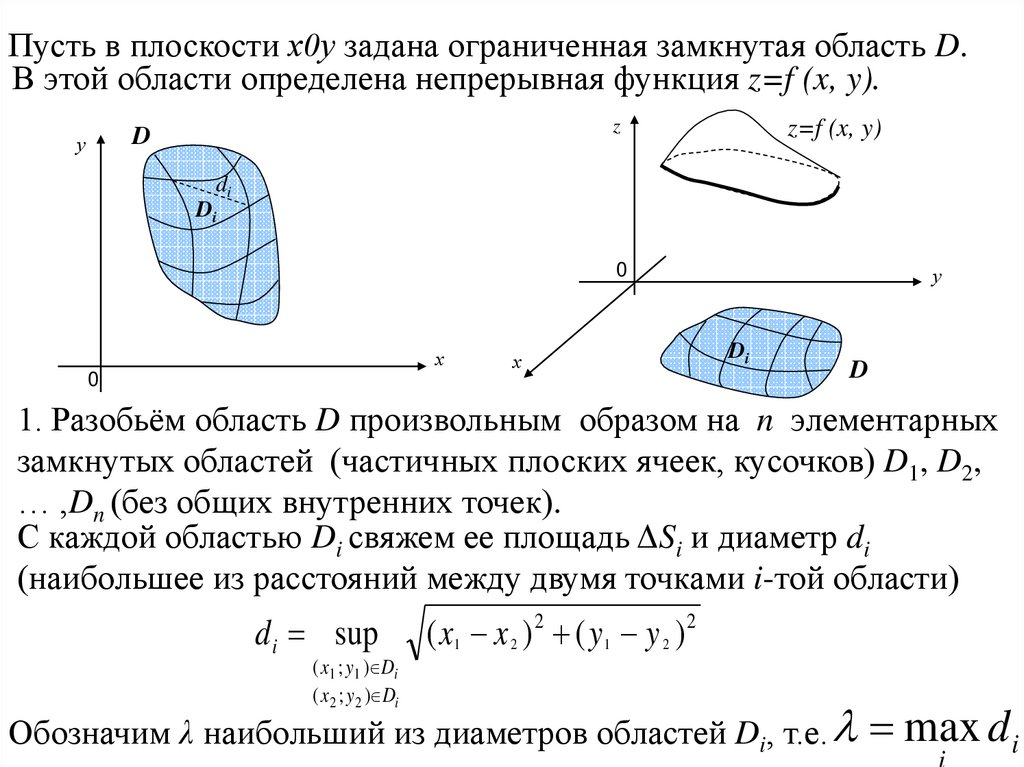
Пусть в плоскости х0у задана ограниченная замкнутая область D.
В этой области определена непрерывная функция z=f (x, y).
z=f (x, y)
z
D
у
di
Di
0
х
0
х
у
Di
D
1. Разобьём область D произвольным образом на n элементарных
замкнутых областей (частичных плоских ячеек, кусочков) D1, D2,
… ,Dn (без общих внутренних точек).
С каждой областью Di свяжем ее площадь ΔSi и диаметр di
(наибольшее из расстояний между двумя точками i-той области)
d i sup
( x1 ; y1 ) Di
( x2 ; y 2 ) Di
( x1 x 2 ) 2 ( y 1 y 2 ) 2
Обозначим λ наибольший из диаметров областей Di, т.е. max d i
i

5.

z
D
у
z=f (x, y)
f (xi , yi)
Рi
Di
0
х
0
х
у
Р
Di i
D
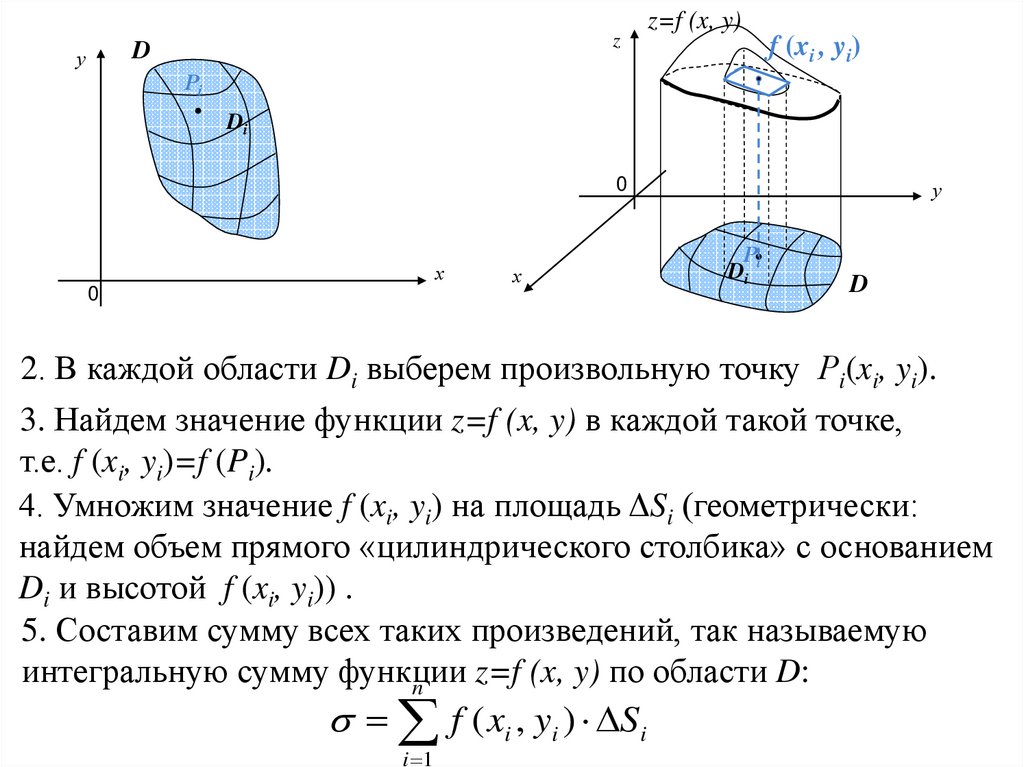
2. В каждой области Di выберем произвольную точку Рi(xi, yi).
3. Найдем значение функции z=f (x, y) в каждой такой точке,
т.е. f (xi, yi)=f (Pi).
4. Умножим значение f (xi, yi) на площадь ΔSi (геометрически:
найдем объем прямого «цилиндрического столбика» с основанием
Di и высотой f (xi, yi)) .
5. Составим сумму всех таких произведений, так называемую
интегральную сумму функции
z=f (x, y) по области D:
n
f ( xi , yi ) Si
i 1

6.

z=f (x, y)
z
n
f (xi , yi)
0
lim f ( xi , yi ) Si f ( x, y )dS
0
у
i 1
f ( x, y)dS f ( x, y)dxdy
D
х
Р
Di i
D
D
D
D – область интегрирования;
х и у – переменные интегрирования;
dS (или dxdy) – элемент площади.
Если существует предел интегральной суммы σ при λ→0,
не зависящий от способа разбиения области D на части
Di и от выбора точек Pi в них, то он называется двойным
интегралом от функции f (x, y) по области D.

7. Условия существования двойного интеграла

• Интегрируемая функция z=f (x, y)
необходимо должна быть ограниченной:
m ≤ f(x,y) ≤ M.
• Достаточное условие интегрируемости
функции. Если функция z=f (x, y)
непрерывна в ограниченной замкнутой
области D, то она интегрируема в этой
области.

8. Основные свойства двойных интегралов

1. k f ( x, y )dxdy k f ( x, y )dxdy
D
D
2. ( f ( x, y ) g ( x, y ))dxdy f ( x, y )dxdy g ( x, y )dxdy
D
D
D
3. f ( x, y )dxdy f ( x, y )dxdy f ( x, y )dxdy
D
D1
D2
Области D1 и D2 не имеют общих внутренних точек и D1 D2 D
4. f ( x, y ) 0 f ( x, y )dxdy 0
D
5. f ( x, y ) g ( x, y ) f ( x, y )dxdy g ( x, y )dxdy
D
6.
f ( x, y)dxdy f ( x, y) dxdy
D
D
D

9. Основные свойства двойных интегралов

7. m f ( x, y ) M m S D f ( x, y )dxdy M S D
D
SD – площадь области D, т и М – наименьшее и наибольшее
значения функции в области D.
8. Если m f ( x, y ) M, то существует такое число : m M
f ( x, y)dxdy S
D
D
9. Если функция f(x,y) непрерывна в области D, то существует
точка ( x0 , y0 ) D такая, что
f ( x, y)dxdy f ( x , y ) S
0
D
0
D

10.

простая относительно оси Ох
простая относительно оси Оу
не является простой