Похожие презентации:
Интеллектуальные системы Лекции 7-8
1.
МТУСИДизайн И. Гайдель 2007
Интеллектуальные системы
Лекции 7-8
2.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Использование сетевых моделей, основанных на сетях Петри (СП),
всегда привлекало исследователей, начиная с момента появления данного
формализма. В настоящее время, с возрастанием интереса к распределенным
структурам, многоагентным системам и алгоритмам взаимодействия отдельных
подсистем, интерес к СП только возрастает.
Аппарат СП широко используется при решении вопросов, связанных с
проектированием и верификацией сложных систем, с построением программных
средств на основе сетевых моделей и оценки возможности распараллеливания
программ, с применением сетевых моделей для описания и анализа
автоматизированных систем, сетевых протоколов, вычислительных сетей,
многопроцессорных системы и др.
Возможности сетей Петри привлекают разработчиков средств
проектирования, в том числе и при разработке средств проектирования с
использованием экспертных систем.
3.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Кроме этого, СП являются инструментом, эффективно поддерживающим
структурный подход к проектированию сложных систем. При использовании
структурного подхода выделяют следующие основные этапы:
1) описание функций, которые должна выполнять проектируемая
система;
2) выработка ряда гипотез, касающихся структур подсистем, из которых
будет состоять проектируемая система (декомпозиция);
3) формирование из данных подсистем законченных структуркандидатов (синтез);
4) проведение анализа каждой синтезированной структуры с целью
определения характеристик и выбор окончательной структуры, наилучшим
образом описывающую систему с заданным функционалом.
Инвариантом при прохождении данных этапов является функционал, заложенный
при описании проектируемой системы.
4.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
При исследовании свойств СП-моделей было показано, что множество
синтезированных СП-моделей (структур-кандидатов), образует метрическое
пространство, на котором можно ввести различные шкалы, количественно
оценивающие каждую СП-модель.
Наличие
механизма
построения
альтернативных
структуркандидатов, а также наличие инструментария количественной оценки данных
структур, позволяет проектировщику получить все множество возможных
структур, реализующих заданный функционал, и выбрать из этого множества
структуры, являющиеся оптимальными по заданному критерию.
Проблема использования описанного подхода на практике состоит в NPсложности задачи получения множества альтернативных вариантов, что
существенно ограничивает практическое использование данного подхода.
Одним из подходов при решении проблем NP-сложности является ввод
ряда ограничивающих условий (построение базы знаний), позволяющих
уменьшить число рассматриваемых вариантов, и тем самым снизить сложность
решаемой задачи.
5.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Одним из методов достижения высокой производительности систем
обработки данных реального времени является использование процессорных
матриц – специализированных вычислительных структур, состоящих из
множества относительно простых устройств (процессорных элементов),
объединённых в однородные параллельные системы.
Рассмотрим подход к проектированию различных конфигураций
матричных процессоров, основанный на структурном анализе сетей Петри и
тензорной методологии.
6.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
7.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Граф потока данных
a33a32a31
a23a22a21
a13a12a11
D
D
D
C31
C32
C33
D
D
D
C21
C22
C23
D
D
D
C11
C12
C13
b11
b12
b13
b21
b22
b23
b31
b32
b33
D - задержки
Задержи введены для
продвижения по индексу К.
Для чего вводятся задержки? В первый момент времени на ПЭ подаются элементы
матрицы А (a11, a21, a31) и матрицы В (b11, b12, b13) . Но к перемножению готов только
ПЭ11 – только на этот ПЭ одновременно подаются элементы матриц А и В (синхронизация).
До ПЭ21 еще не дошел элемент b11, до ПЭ12 не дошел элемент a11. Это будет сделано
только на следующем такте работы МП. До остальных ПЭ данные дойдут еще с большей
задержкой. Поэтому на ПЭ вводится задержка, для организации одновременной подачи
входных данных.
8.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Оценим, в чем преимущество матричных процессоров.
Для этого определим - за сколько тактов будет выполнена операция умножения А(3,3) ×
В(3,3) на однопроцессорном компьютере.
Будем считать, что за один такт происходят операции умножения элементов матриц А и В
(αik × bkj) , а также сложение полученного произведения с частичной суммой.
Что такое частичная сумма?
c'11 = α11×b11
-
и c’’11 = α11×b11 + α12×b21
это примеры частичных сумм.
c11 = α11×b11 + α12×b21 + α13×b31
-
полная сумма, описывающая получение элемента с11 матрицы С.
9.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Пусть матричный процессор и соответствующий процессорный элемент (ПЭ) имеют
следующий вид:
Подача элементов
матрицы В
накапливающий регистр для
формирования частичных сумм
умножитель
сумматор
a
b
Подача элементов
матрицы А
Матричный процессор
Структура процессорного элемента
10.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
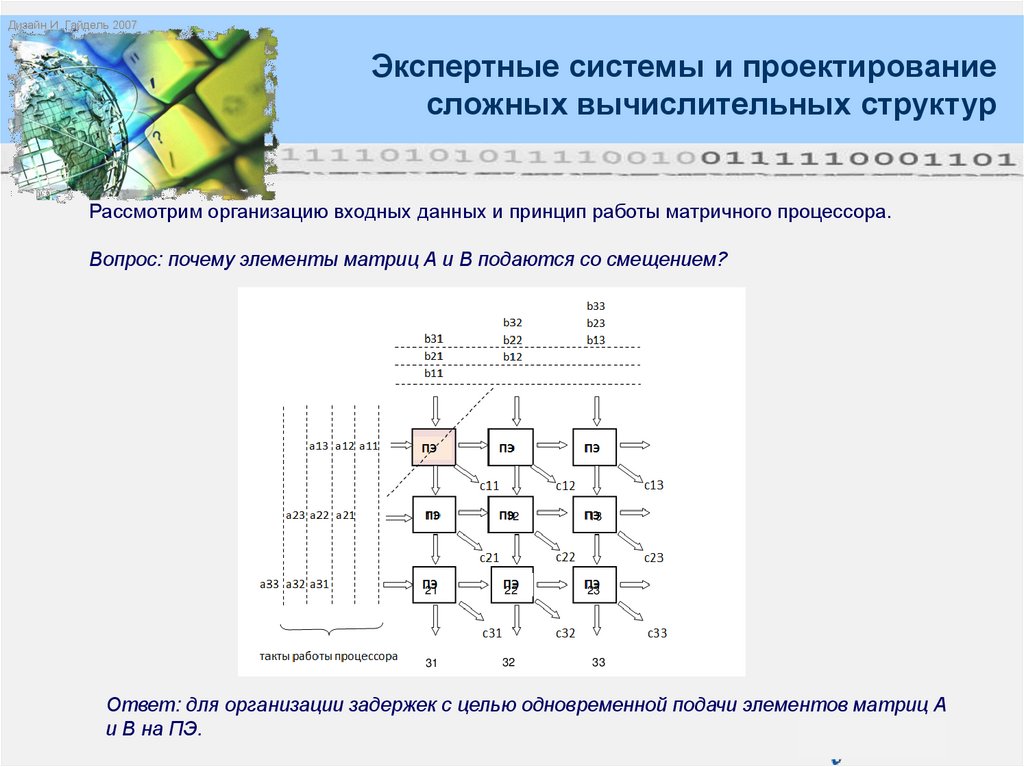
Рассмотрим организацию входных данных и принцип работы матричного процессора.
Вопрос: почему элементы матриц А и В подаются со смещением?
11
12
13
21
22
23
31
32
33
Ответ: для организации задержек с целью одновременной подачи элементов матриц А
и В на ПЭ.
11.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
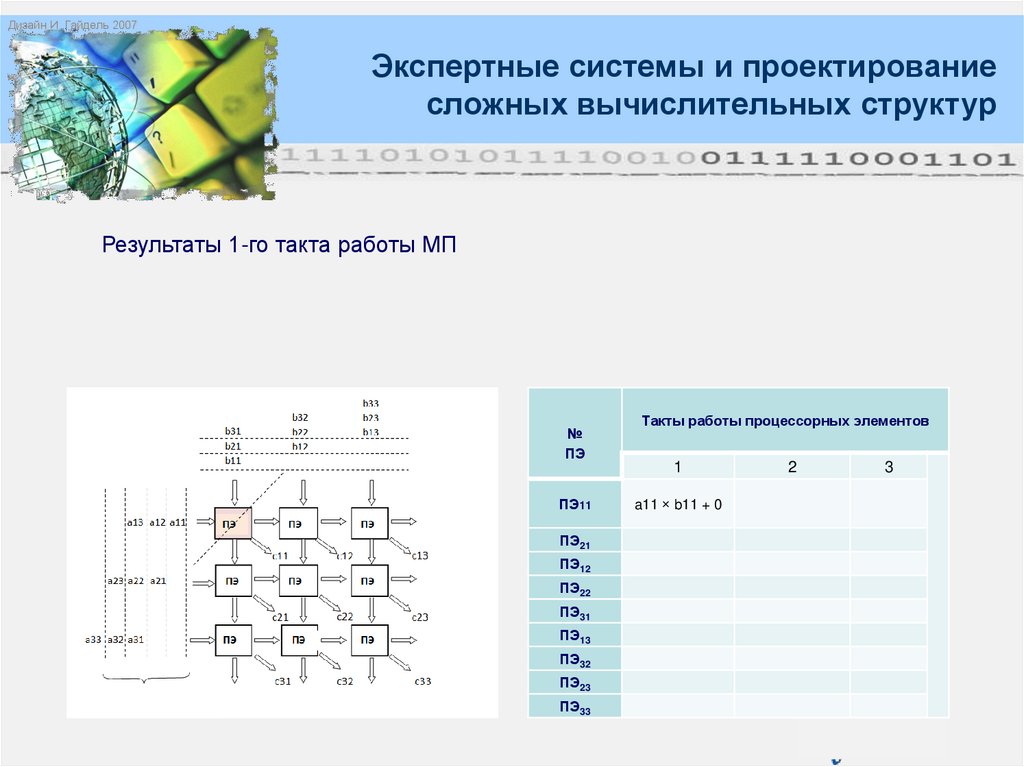
Результаты 1-го такта работы МП
№
ПЭ
ПЭ11
ПЭ21
ПЭ12
ПЭ22
ПЭ31
ПЭ13
ПЭ32
ПЭ23
ПЭ33
Такты работы процессорных элементов
1
a11 × b11 + 0
2
3
12.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Результаты 2-го такта работы МП
№
ПЭ
Такты работы процессорных элементов
1
2
ПЭ11
a11 × b11 + 0
a11 × b11
+ a12 × b21
ПЭ21
0+0
a21 × b11
ПЭ12
ПЭ22
ПЭ31
ПЭ13
ПЭ32
ПЭ23
ПЭ33
a11 × b12
3
13.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
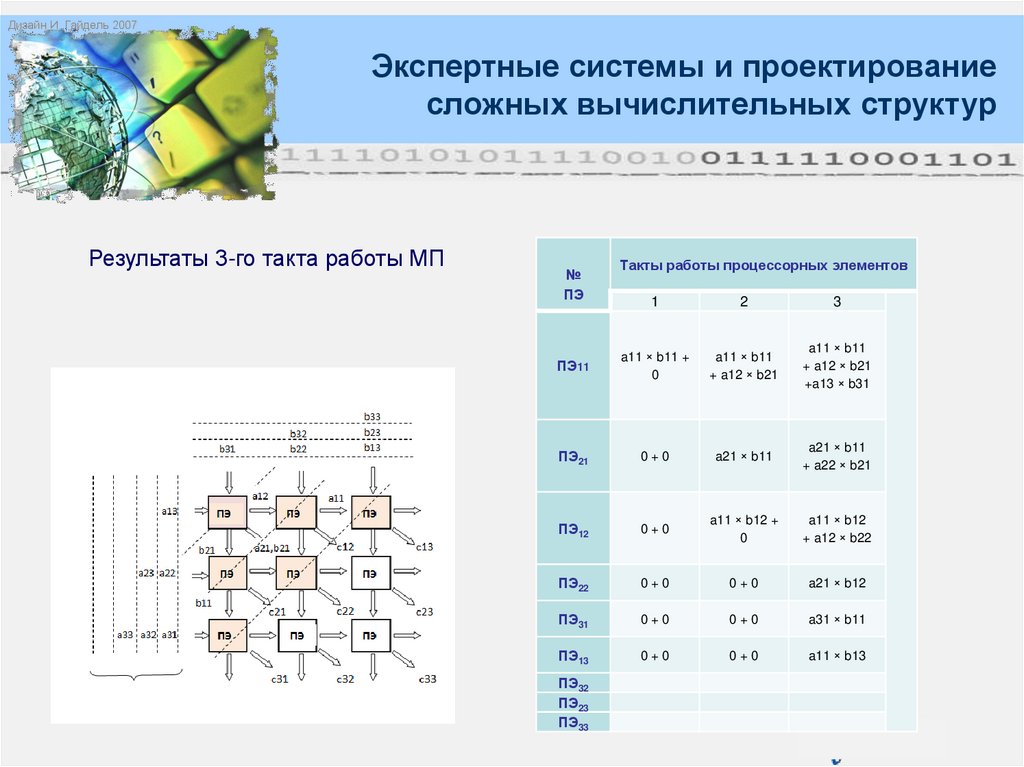
Результаты 3-го такта работы МП
№
ПЭ
Такты работы процессорных элементов
1
2
3
ПЭ11
a11 × b11 +
0
a11 × b11
+ a12 × b21
a11 × b11
+ a12 × b21
+a13 × b31
ПЭ21
0+0
a21 × b11
a21 × b11
+ a22 × b21
ПЭ12
0+0
a11 × b12 +
0
a11 × b12
+ a12 × b22
ПЭ22
0+0
0+0
a21 × b12
ПЭ31
0+0
0+0
a31 × b11
ПЭ13
0+0
0+0
a11 × b13
ПЭ32
ПЭ23
ПЭ33
14.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
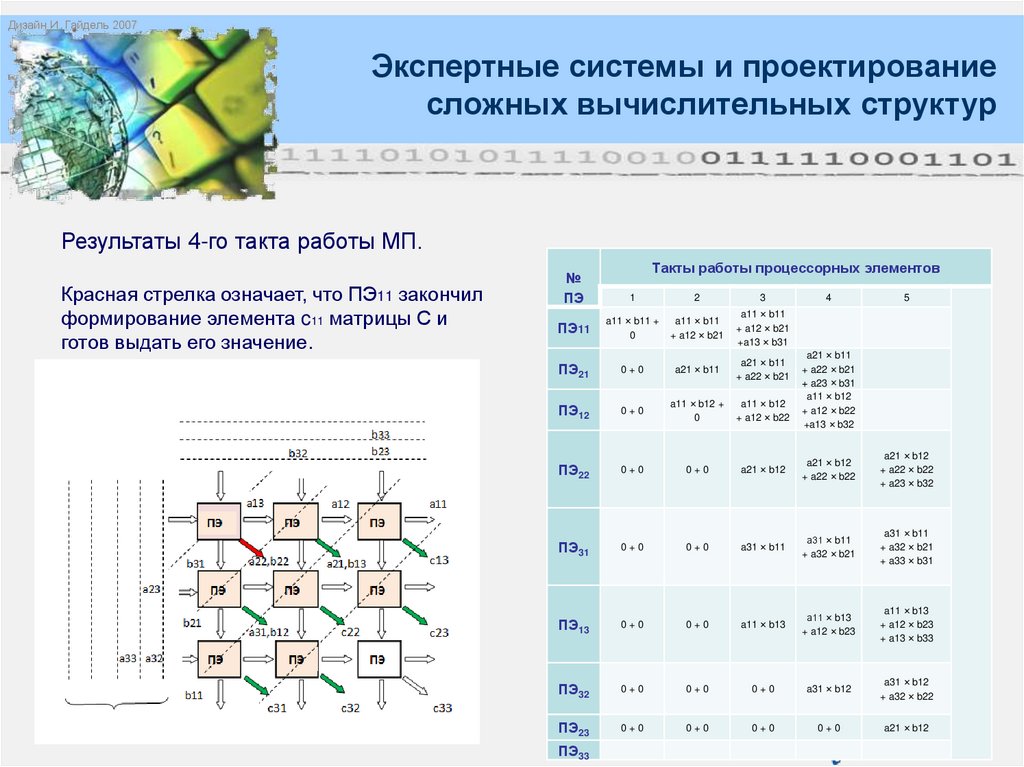
Результаты 4-го такта работы МП.
Красная стрелка означает, что ПЭ11 закончил
формирование элемента c11 матрицы С и
готов выдать его значение.
№
ПЭ
Такты работы процессорных элементов
1
2
3
4
5
ПЭ11
a11 × b11 +
0
a11 × b11
+ a12 × b21
a11 × b11
+ a12 × b21
+a13 × b31
ПЭ21
0+0
a21 × b11
a21 × b11
+ a22 × b21
ПЭ12
0+0
a11 × b12 +
0
a11 × b12
+ a12 × b22
ПЭ22
0+0
0+0
a21 × b12
a21 × b12
+ a22 × b22
a21 × b12
+ a22 × b22
+ a23 × b32
ПЭ31
0+0
0+0
a31 × b11
а31 × b11
+ a32 × b21
a31 × b11
+ a32 × b21
+ a33 × b31
ПЭ13
0+0
0+0
a11 × b13
а11 × b13
+ a12 × b23
a11 × b13
+ a12 × b23
+ a13 × b33
ПЭ32
0+0
0+0
0+0
a31 × b12
a31 × b12
+ a32 × b22
ПЭ23
0+0
0+0
0+0
0+0
a21 × b12
ПЭ33
a21 × b11
+ a22 × b21
+ a23 × b31
a11 × b12
+ a12 × b22
+a13 × b32
15.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
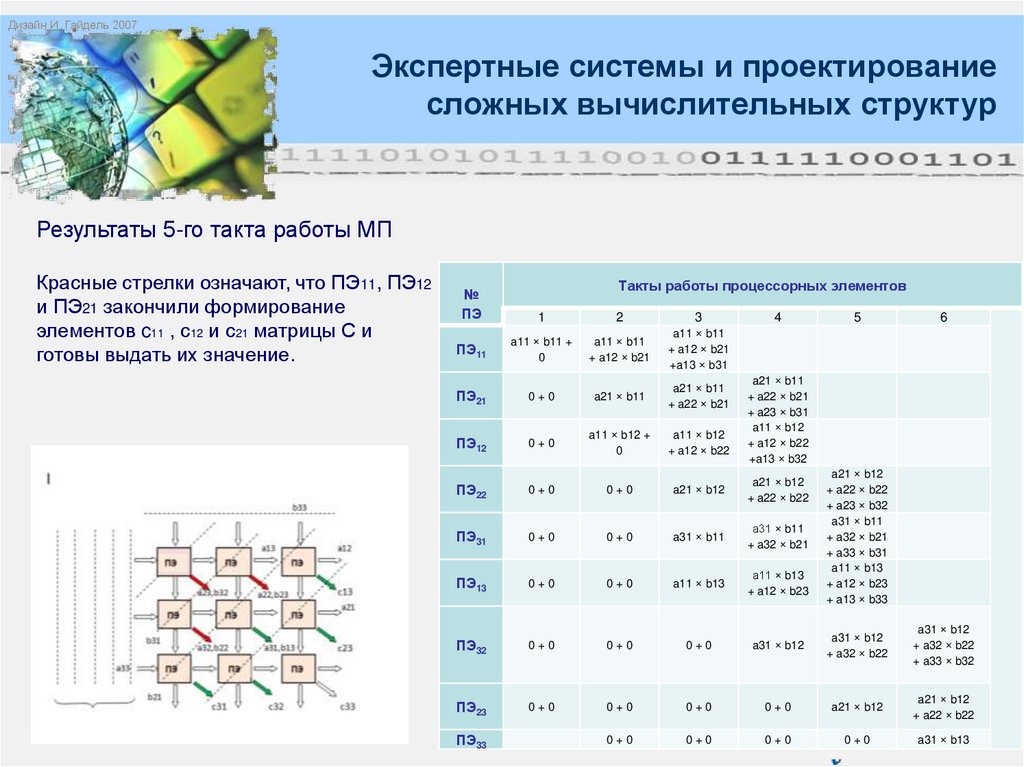
Результаты 5-го такта работы МП
Красные стрелки означают, что ПЭ11, ПЭ12
и ПЭ21 закончили формирование
элементов c11 , с12 и с21 матрицы С и
готовы выдать их значение.
№
ПЭ
Такты работы процессорных элементов
1
2
3
4
5
6
ПЭ11
a11 × b11 +
0
a11 × b11
+ a12 × b21
a11 × b11
+ a12 × b21
+a13 × b31
ПЭ21
0+0
a21 × b11
a21 × b11
+ a22 × b21
ПЭ12
0+0
a11 × b12 +
0
a11 × b12
+ a12 × b22
ПЭ22
0+0
0+0
a21 × b12
a21 × b12
+ a22 × b22
ПЭ31
0+0
0+0
a31 × b11
а31 × b11
+ a32 × b21
ПЭ13
0+0
0+0
a11 × b13
а11 × b13
+ a12 × b23
ПЭ32
0+0
0+0
0+0
a31 × b12
a31 × b12
+ a32 × b22
a31 × b12
+ a32 × b22
+ a33 × b32
ПЭ23
0+0
0+0
0+0
0+0
a21 × b12
a21 × b12
+ a22 × b22
0+0
0+0
0+0
0+0
a31 × b13
ПЭ33
a21 × b11
+ a22 × b21
+ a23 × b31
a11 × b12
+ a12 × b22
+a13 × b32
a21 × b12
+ a22 × b22
+ a23 × b32
a31 × b11
+ a32 × b21
+ a33 × b31
a11 × b13
+ a12 × b23
+ a13 × b33
16.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
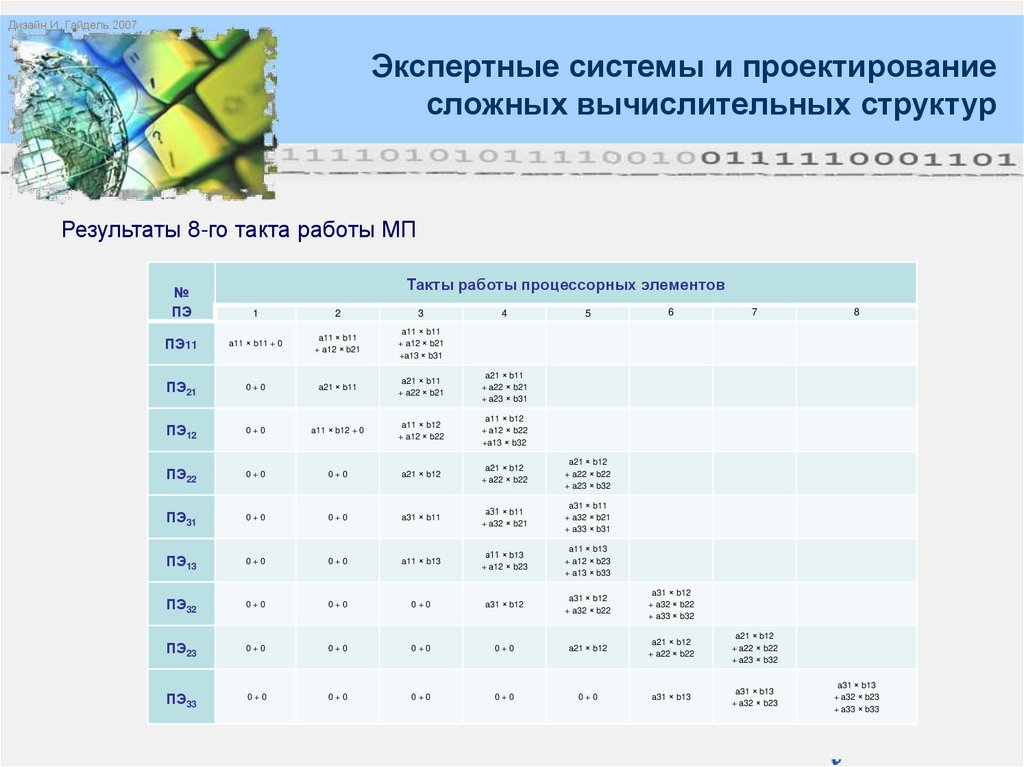
Результаты 8-го такта работы МП
№
ПЭ
Такты работы процессорных элементов
1
2
3
4
5
6
7
ПЭ11
a11 × b11 + 0
a11 × b11
+ a12 × b21
a11 × b11
+ a12 × b21
+a13 × b31
ПЭ21
0+0
a21 × b11
a21 × b11
+ a22 × b21
a21 × b11
+ a22 × b21
+ a23 × b31
ПЭ12
0+0
a11 × b12 + 0
a11 × b12
+ a12 × b22
a11 × b12
+ a12 × b22
+a13 × b32
ПЭ22
0+0
0+0
a21 × b12
a21 × b12
+ a22 × b22
a21 × b12
+ a22 × b22
+ a23 × b32
ПЭ31
0+0
0+0
a31 × b11
а31 × b11
+ a32 × b21
a31 × b11
+ a32 × b21
+ a33 × b31
ПЭ13
0+0
0+0
a11 × b13
а11 × b13
+ a12 × b23
a11 × b13
+ a12 × b23
+ a13 × b33
ПЭ32
0+0
0+0
0+0
a31 × b12
a31 × b12
+ a32 × b22
a31 × b12
+ a32 × b22
+ a33 × b32
ПЭ23
0+0
0+0
0+0
0+0
a21 × b12
a21 × b12
+ a22 × b22
a21 × b12
+ a22 × b22
+ a23 × b32
ПЭ33
0+0
0+0
0+0
0+0
0+0
a31 × b13
a31 × b13
+ a32 × b23
8
a31 × b13
+ a32 × b23
+ a33 × b33
17.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
Вывод.
На матричном процессоре результат умножения матриц А(3,3) × В(3,3)
будет получен за 8 тактов.
Матричные процессоры эффективные устройства, позволяющие решать
определенный круг
задач с существенным ускорением.
Но они
эффективны только для определенного круга задач. Существуют задачи,
при решении которых эффективность МП теряется.
18.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
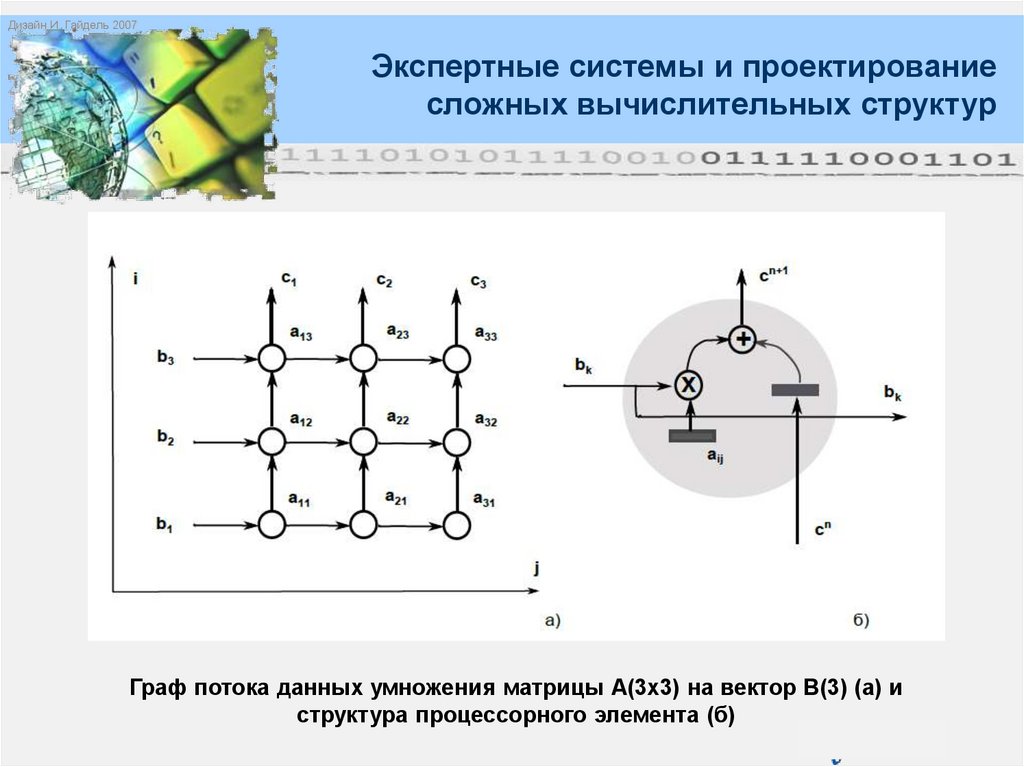
Граф потока данных умножения матрицы А(3х3) на вектор В(3) (а) и
структура процессорного элемента (б)
19.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
а)
б)
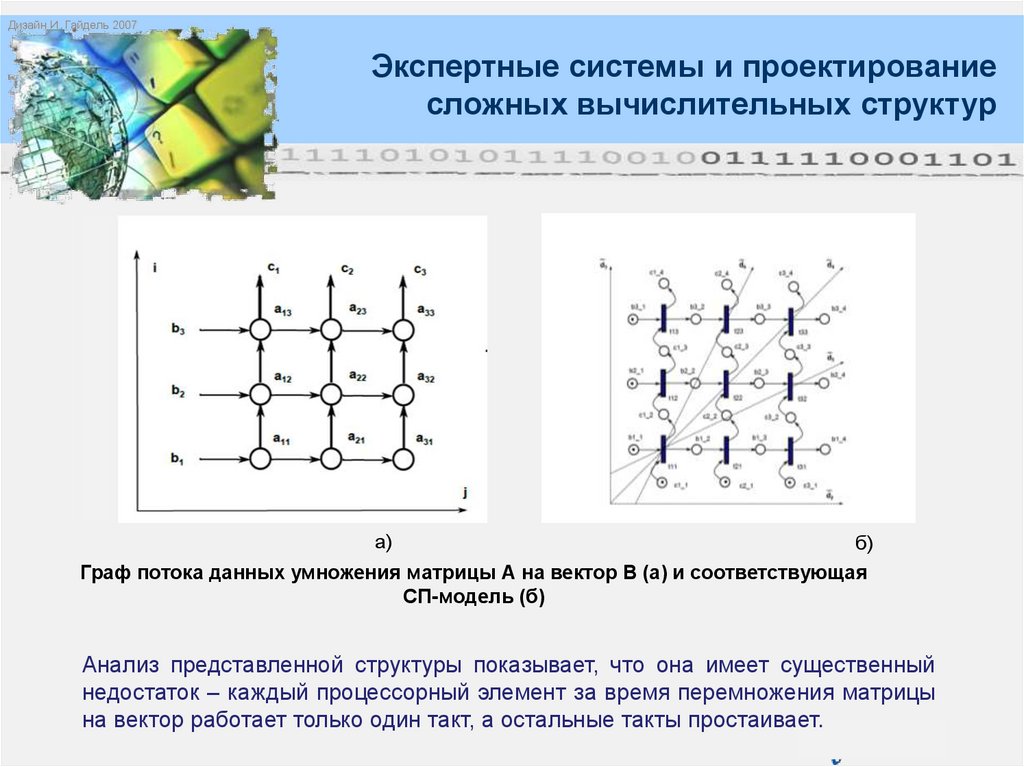
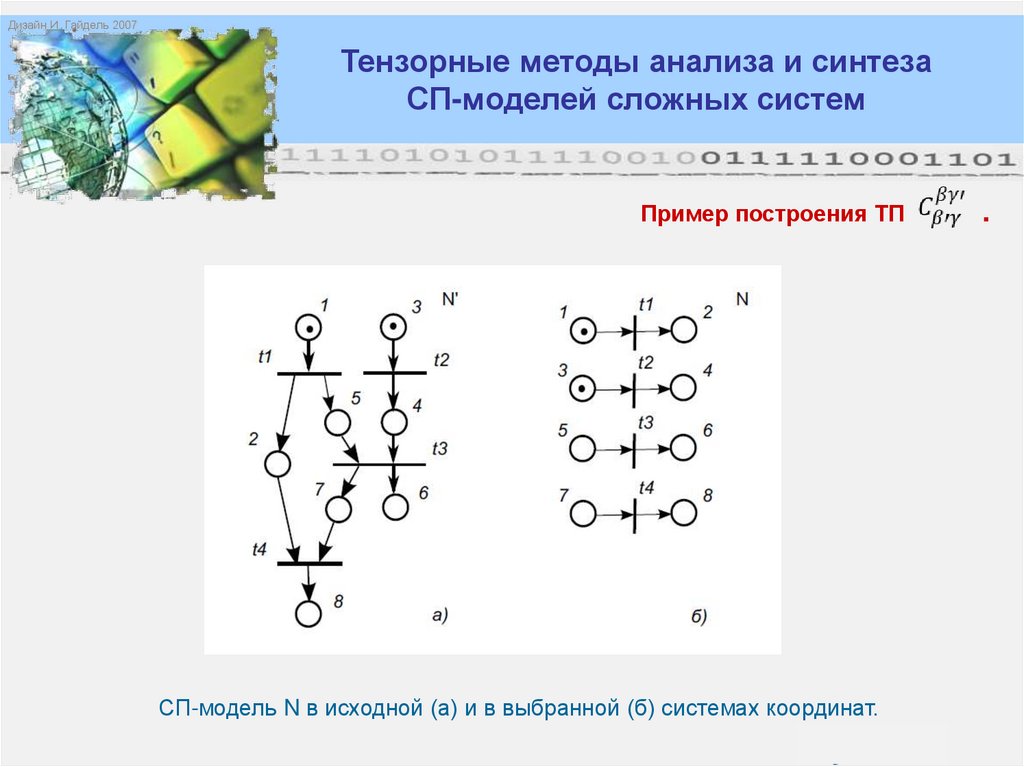
Граф потока данных умножения матрицы А на вектор В (а) и соответствующая
СП-модель (б)
Анализ представленной структуры показывает, что она имеет существенный
недостаток – каждый процессорный элемент за время перемножения матрицы
на вектор работает только один такт, а остальные такты простаивает.
20.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
СП-модели параллельных структур умножения матрицы А на вектор В,
полученные в результате проекций d2 – d4
21.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
а)
б)
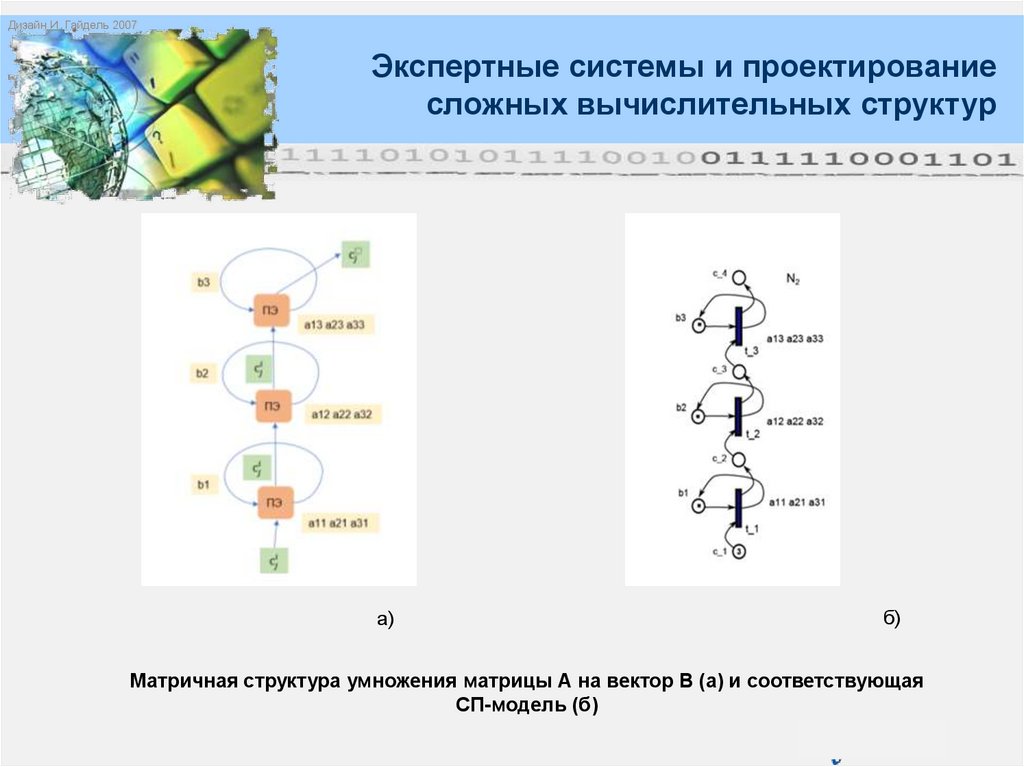
Матричная структура умножения матрицы А на вектор В (а) и соответствующая
СП-модель (б)
22.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
а)
б)
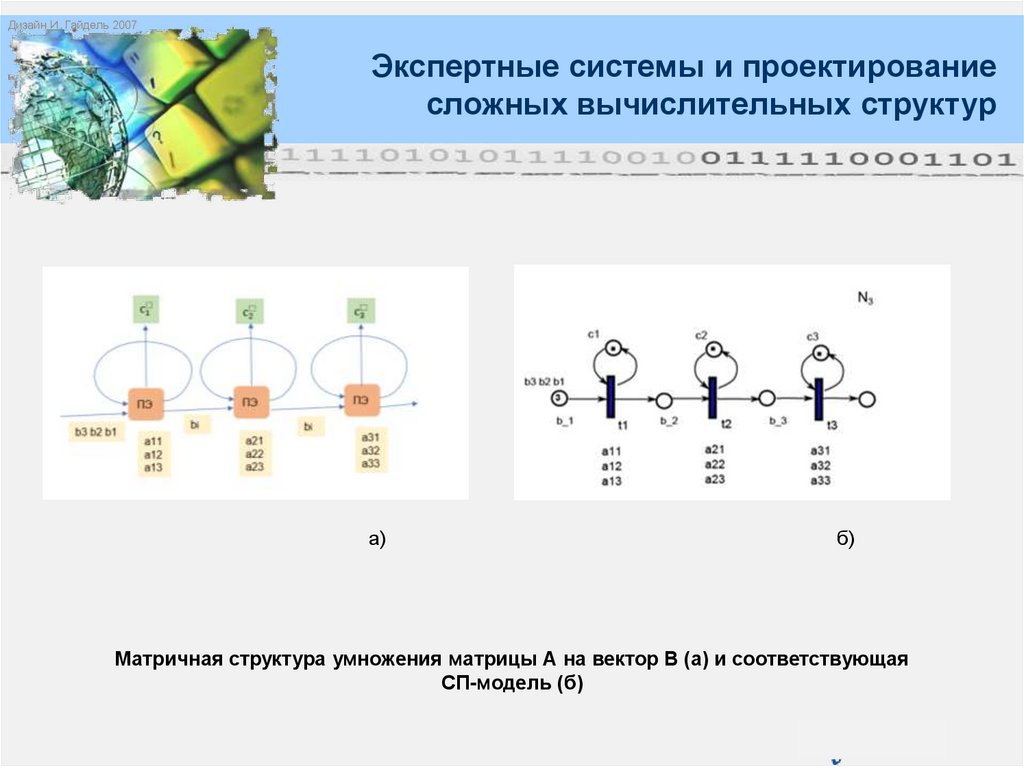
Матричная структура умножения матрицы А на вектор В (а) и соответствующая
СП-модель (б)
23.
Дизайн И. Гайдель 2007Экспертные системы и проектирование
сложных вычислительных структур
СП-модели параллельных структур умножения матрицы А на вектор В,
полученные в результате проекций d5 – d6
Анализ представленных линейных структур показывает, что ПЭ элементы в
них загружены уже большее время, а не только в течение одного такта.
24.
МТУСИДизайн И. Гайдель 2007
Интеллектуальные системы
Лекции 9
25.
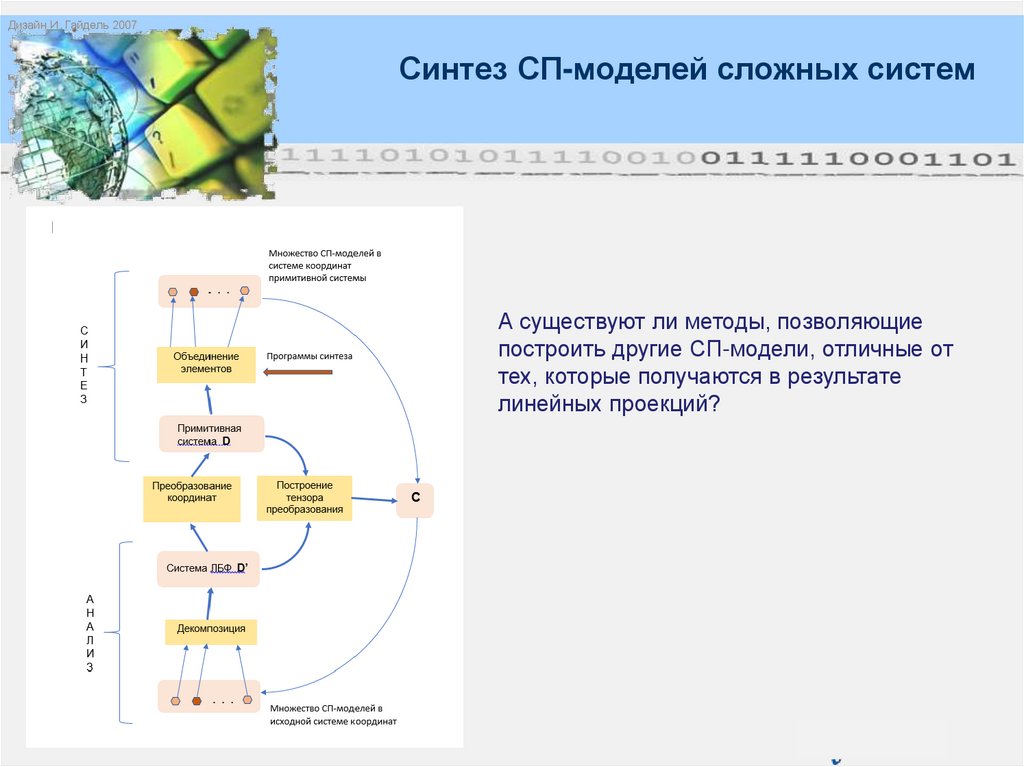
Дизайн И. Гайдель 2007Синтез СП-моделей сложных систем
А существуют ли методы, позволяющие
построить другие СП-модели, отличные от
тех, которые получаются в результате
линейных проекций?
26.
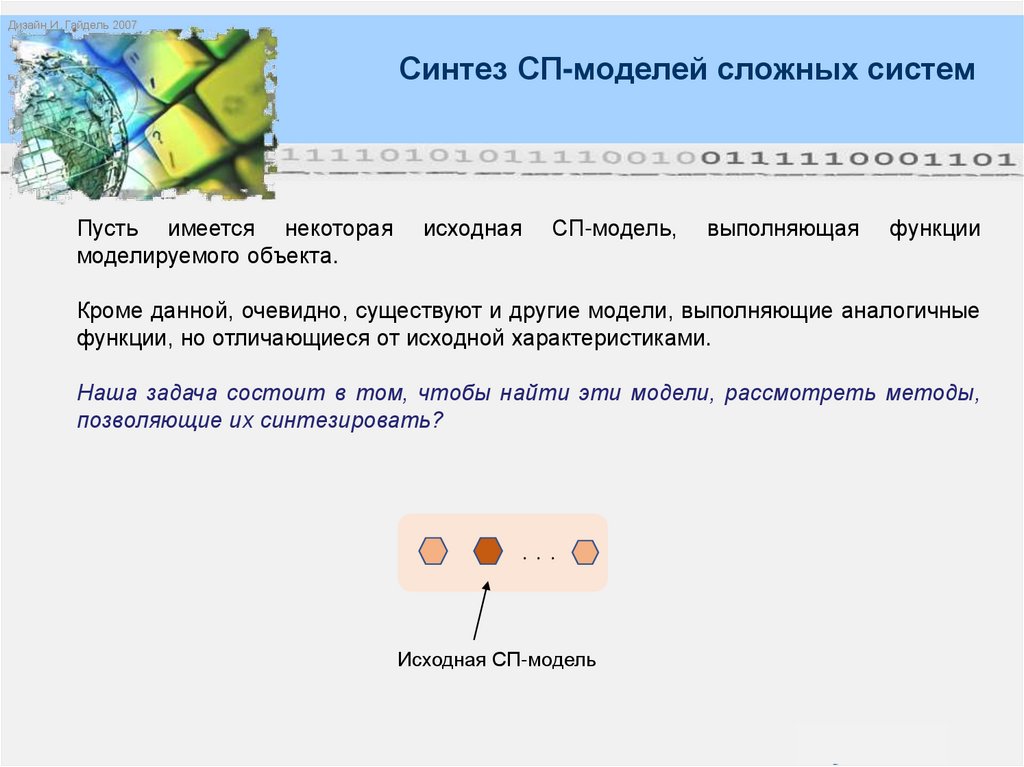
Дизайн И. Гайдель 2007Синтез СП-моделей сложных систем
Пусть имеется некоторая
моделируемого объекта.
исходная
СП-модель,
выполняющая
функции
Кроме данной, очевидно, существуют и другие модели, выполняющие аналогичные
функции, но отличающиеся от исходной характеристиками.
Наша задача состоит в том, чтобы найти эти модели, рассмотреть методы,
позволяющие их синтезировать?
. . .
Исходная СП-модель
27.
Дизайн И. Гайдель 2007Синтез СП-моделей сложных систем
На первом шаге к синтезу новых
моделей, мы осуществляем анализ
имеющейся исходной СП-модели.
Проводим декомпозицию модели с
целью получения составных линейных
или линейно-циклических фрагментов
(линейные базовые фрагменты ЛБФ).
Почему линейных?
1. Потому что линейные фрагменты
легко описываются и просты для
последующего исследования.
2. Будем
считать,
что
линейные
фрагменты
задают
множество
правил
(последовательность
выполнения
операций),
которые
нельзя нарушать.
28.
Дизайн И. Гайдель 2007Декомпозиция СП-моделей (анализ)
Мы уже говорили, что декомпозиция используется тогда, когда
необходимо
анализировать
сложную
систему,
которую
трудно
рассматривать как одно целое.
При этом предлагалось сложную систему разбить на несколько
составляющих подсистем (подвергнуть декомпозиции), которые в
отдельности легче исследовать. После того, как каждая составляющая
подсистема исследована в отдельности, объединить их в одно целое
несравненно легче, чем анализировать исходную систему.
В итоге сущность декомпозиционных методов заключается:
- в разбиении сложной системы на более простые,
- в исследовании этих простых систем,
- в объединении результатов с целью получения некоторого целостного и
единого решения.
29.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
Операции над вершинами сетей Петри
Для проведения анализа и синтеза сетевых моделей необходимы
средства, позволяющие преобразовывать СП-модели.
С этой целью рассмотрим операции разделения и объединения вершин
СП.
СП, в которой P = {p', p''}, T={t}, p' pre(t) и p'' post(t), есть элементарная сеть.
СП, состоящую из множества
примитивной системой NPR.
элементарных
сетей,
будем
называть
30.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
Объединение вершин СП-моделей
Определение 1. Объединением переходов ti и tj (ti + tj ) является переход tij , для
которого справедливо:
pre (tij ) = pre (ti ) ∪ pre (tj); post (tij ) = post (ti ) ∪ post (tj).
Определение 2. Объединением позиций pi и pj (pi + pj ) является позиция pij , для
которой справедливо:
pre (pij) = pre (pi) ∪ pre (pj); post (pij) = post (pi) ∪ post (pj); (pij) = max ( (pi) , ( (pj)).
31.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
Разделение вершин
При декомпозиции делению подвергаются вершины, которые удовлетворяют
следующим условиям:
|pre(t)| + |post(t)| > 2 ,
|pre(p)| > 1 или |post(p)| > 1 .
32.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
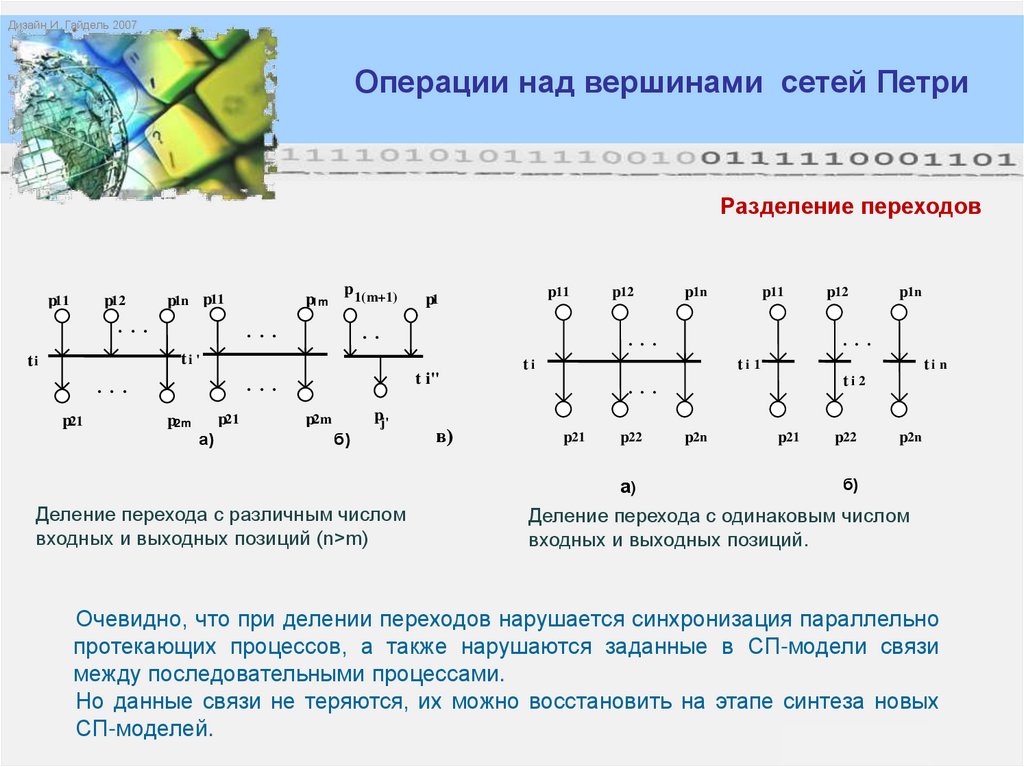
Разделение переходов
p11
p12
p1n p11
p1m
p 1(m+1)
. . .
. .
.
ti '
p1n
p11
p21
p2m
а)
. . .
t i"
. . .
. . .
p21
p12
p12
p1n
n
. . .
ti
p11
p1
p2m
б)
pj'
в)
ti
ti 1
ti n
ti 2
. . .
p21
p22
а)
Деление перехода с различным числом
входных и выходных позиций (n>m)
. . .
p2n
p21
p22
p2n
б)
Деление перехода с одинаковым числом
входных и выходных позиций.
Очевидно, что при делении переходов нарушается синхронизация параллельно
протекающих процессов, а также нарушаются заданные в СП-модели связи
между последовательными процессами.
Но данные связи не теряются, их можно восстановить на этапе синтеза новых
СП-моделей.
33.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
Разделение позиций. Деление головной позиции
.
pj
.
...
ti1
ti2
tin
a)
pj1
. pj2
. pjn
ti1
ti2
tin
б)
Определение 3 (деление головной позиции). Если для позиции pj выполняются
условия: pre(pj) = и post(pj) = {ti1, ti2, ..., tin }, то позиция pj делится на n позиций
(pj1, pj2, ..., pjk, ..., pjn), для которых справедливо:
pre(pjk) = , post(pjk) = {tik}, (pjk) = (pj) , где 1 <= k <= n .
34.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
Разделение позиций. Деление хвостовой позиции
t i1
t i2
. . .
t in
t i1
t i2
.
.
pj1
t in
. . . . .
p j2
p jn
pj
а)
б)
Определение 4 (деление хвостовой позиции). Если для позиции pj выполняются
условия: pre(pj )={ti1, ti2, ..., tin} и post(pj) = , то позиция pj делится на n позиций
(pj1, pj2, ..., pjk, ..., pjn), для которых справедливо:
pre(pjk) = {tik} , post(pjk) = , (pjk) = (pj) , где 1 k n .
35.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
t11
t12
Деление позиции с одинаковым числом
входных и выходных переходов
t1n
t11
t12
t1n
pj1
pj2
pjn
...
pj
...
...
t21
t22
t2n
ti1
ti2
tin
a)
б)
Определение 3. Деление позиции с одинаковым числом входных и
выходных переходов.
Если для позиции pj выполняются условия: pre(pj) = {t11, t12,..., t1n } и
post(pj) = {t21, t22,..., t2n }, то данная позиция делится на n позиций (pj1,
pj2,..., pjn ), для которых справедливо: pre(pjk) = {t1k} , post(pjk) = {t2k} , где
1<=k<=n. (pjk) = (pj) , где 1 <= k <= n .
36.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
t11
t12 t1m
t11
...
...
pj
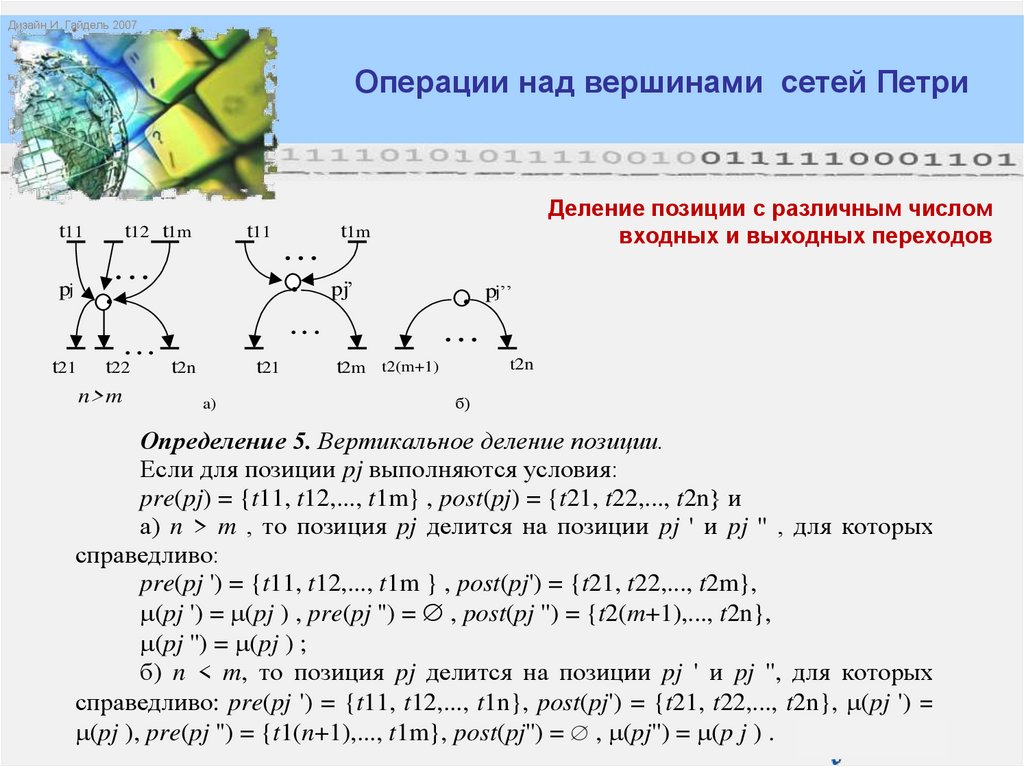
Деление позиции с различным числом
входных и выходных переходов
t1m
.
.
pj’
. pj’’
...
...
...
t21
t22
n>m
t2n
t21
a)
t2m
t2n
t2(m+1)
б)
Определение 5. Вертикальное деление позиции.
Если для позиции pj выполняются условия:
pre(pj) = {t11, t12,..., t1m} , post(pj) = {t21, t22,..., t2n} и
а) n > m , то позиция pj делится на позиции pj ' и pj '' , для которых
справедливо:
pre(pj ') = {t11, t12,..., t1m } , post(pj') = {t21, t22,..., t2m},
(pj ') = (pj ) , pre(pj '') = , post(pj '') = {t2(m+1),..., t2n},
(pj '') = (pj ) ;
б) n < m, то позиция pj делится на позиции pj ' и pj '', для которых
справедливо: pre(pj ') = {t11, t12,..., t1n}, post(pj') = {t21, t22,..., t2n}, (pj ') =
(pj ), pre(pj '') = {t1(n+1),..., t1m}, post(pj'') = , (pj'') = (p j ) .
37.
Дизайн И. Гайдель 2007Операции над вершинами сетей Петри
Разделение вершин СП-моделей
При делении позиций и переходов часто имеет смысл сохранять максимально
длинную последовательность вершин (цепочку процессов), заданную исходной СПмоделью. Это позволяет в дальнейшем, при синтезе новых СП-моделей,
формировать дополнительные ограничения и сокращает число вариантов
синтезируемых СП-моделей.
Вывод: разделение позиций и переходов СП-моделей необходимо связывать с
построением множества ограничивающих условий (базы знаний), которые будут
учитываться при синтезе новых СП-моделей и существенно сокращать число
рассматриваемых моделей.
Пример
38.
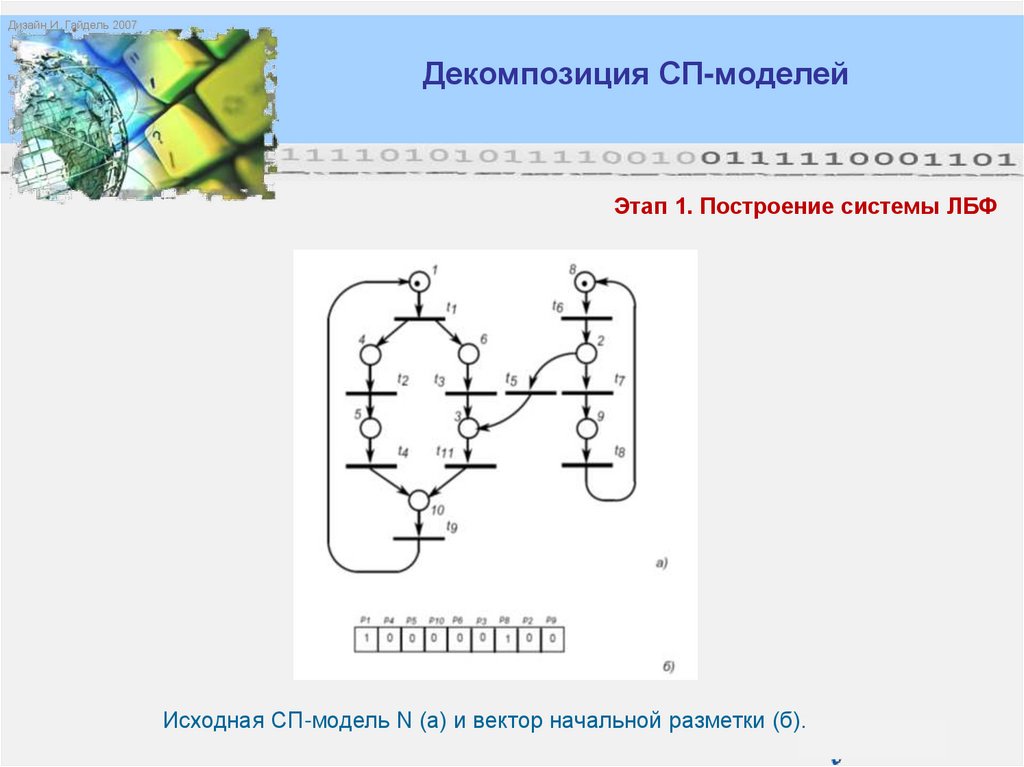
Дизайн И. Гайдель 2007Декомпозиция СП-моделей
Этап 1. Построение системы ЛБФ
Исходная СП-модель N (а) и вектор начальной разметки (б).
39.
Дизайн И. Гайдель 2007Декомпозиция СП-моделей
Этап 1. Построение системы ЛБФ. Выделение циклов
Обобщенная матрица A исходной СП-модели N
A =
1. Для чего мы построили обобщенную
матрицу А?
2. На какой вопрос отвечает матрица
инцидентности
(представляющая
граф),
возводимая в степень?
40.
Дизайн И. Гайдель 2007Декомпозиция СП-моделей
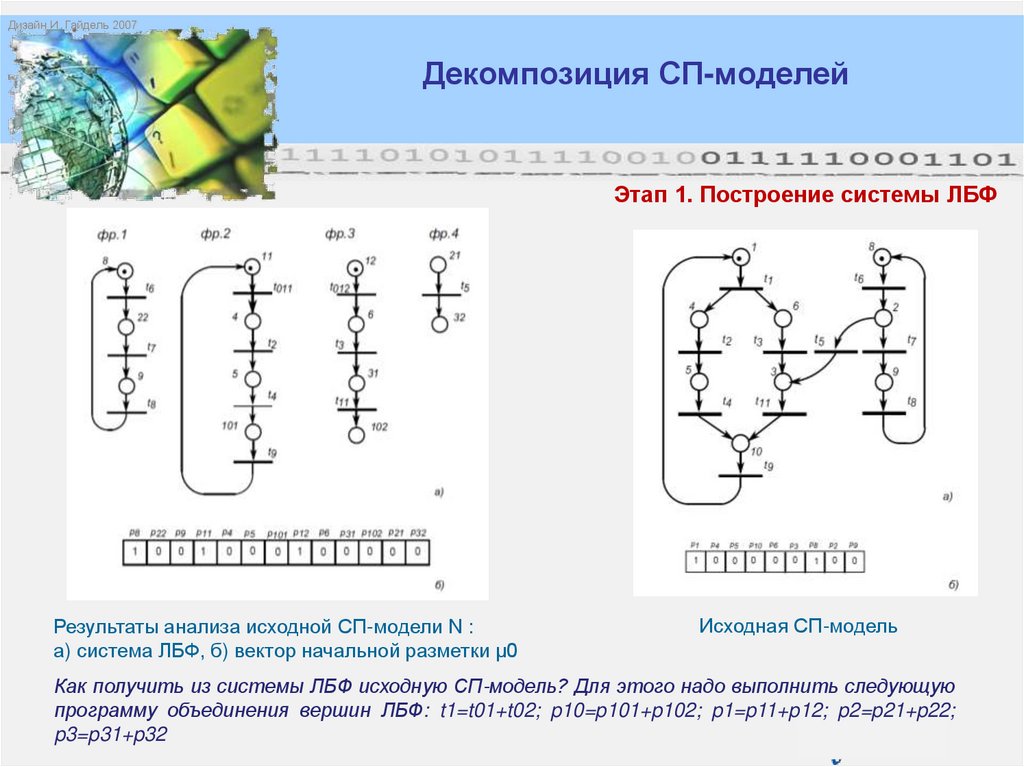
Этап 1. Построение системы ЛБФ
Результаты анализа исходной СП-модели N :
а) система ЛБФ, б) вектор начальной разметки μ0
Исходная СП-модель
Как получить из системы ЛБФ исходную СП-модель? Для этого надо выполнить следующую
программу объединения вершин ЛБФ: t1=t01+t02; p10=p101+p102; p1=p11+p12; p2=p21+p22;
p3=p31+p32
41.
Дизайн И. Гайдель 2007Декомпозиция СП-моделей
Этап 2. Построение примитивной системы
Примитивная система NPR (а), соответствующая
исходной СП-модели N, и вектор начальной разметки (б).
Система ЛБФ
42.
Дизайн И. Гайдель 2007Декомпозиция СП-моделей
Этап 2. Построение примитивной системы
Для чего построена примитивная система?
Примитивная
система
отражает
состав
элементов, из которых построена исходная
СП-модель.
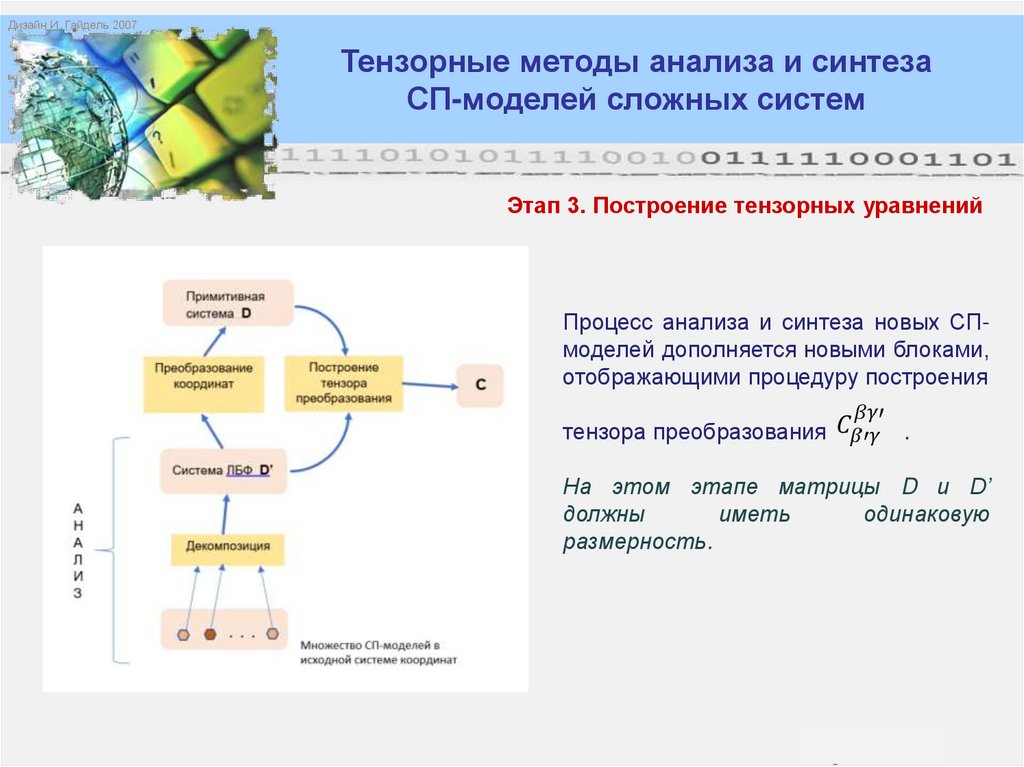
Примечание: число переходов в системе ЛБФ и в
примитивной системе совпадает, а число позиций
не совпадает, что приводит к тому, что матрицы
D и D’ имеют разные размерности. Следовательно,
для выполнения операций между матрицами D и D’
необходимо выровнять размерности матриц.
Будем
считать,
что
система
ЛБФ
и
примитивная система представляют одну и ту
же СП, но выраженную в разных системах
координат. Связь между СП, выраженными в
разных системах координат, осуществляется с
помощью
тензоров
(операторы
преобразования).
43.
Дизайн И. Гайдель 2007Тензорные методы анализа и синтеза
СП-моделей сложных систем
Этап 3. Построение тензорных уравнений.
Типы геометрий
Евклидова геометрия - допускает преобразования, не меняющие форму фигур.
При этом можно переносить, вращать, изменять масштаб фигур.
Афинная геометрия в дополнение к преобразованиям геометрии Евклида
допускает такие деформации фигур, при которых сохраняются условия
прямолинейности и параллельности линий. Например, параллелограмм и
квадрат в данной геометрии представляют одну и ту же геометрическую фигуру.
В проективной геометрии в результате преобразований должно сохраняться
условие прямолинейности.
В топологии допустимы почти любые преобразования, но при этом должно
сохраняться свойство принадлежности (точки, по-прежнему, должны
принадлежать линиям, линии - поверхностям и т.д.).
44.
Дизайн И. Гайдель 2007Тензорные методы анализа и синтеза
СП-моделей сложных систем
Этап 3. Построение тензорных уравнений.
Типы геометрий
Тензорному анализу соответствует своя геометрия – геометрия разрыва.
Для того, чтобы определить геометрию тензорного анализа необходимо
определить такие понятия, как:
-
пространство,
-
размерность,
-
система координат,
-
преобразование системы координат.
45.
Дизайн И. Гайдель 2007Тензорные методы анализа и синтеза
СП-моделей сложных систем
Этап 3. Построение тензорных уравнений.
Постулаты обобщений
Постулат первого обобщения.
Метод анализа и окончательные уравнения, описывающие поведение сложной
физической системы, могут быть найдены последовательно при анализе
простейшего, но наиболее общего элемента системы при условии, что каждая
величина заменяется соответствующей n-матрицей.
Постулат второго обобщения является фундаментальным предположением
тензорного анализа и состоит в следующем:
1) новая система описывается тем же числом n-матриц и того же типа,
что и старая система, но отличается от нее численным значением компонент nматриц;
2) уравнение новой системы, записанное в n-матрицах, имеет тот же
вид, что и уравнение старой системы;
3) n-матрицы новой системы могут быть найдены из n-матриц старой
системы с помощью рутинного преобразования.
46.
Дизайн И. Гайдель 2007Тензорные методы анализа и синтеза
СП-моделей сложных систем
Этап 3. Построение тензорных уравнений.
Постулаты обобщений
Вывод:
переход от одного способа соединения блоков некоторой системы к другому
не требует введения новых n-матриц и изменения формы уравнений. Отличие
состоит в том, что n-матрицы, принадлежащие разным уравнениям, имеют
разные компоненты.
47.
Дизайн И. Гайдель 2007Тензорные методы анализа и синтеза
СП-моделей сложных систем
Этап 3. Построение тензорных уравнений.
48.
Дизайн И. Гайдель 2007Тензорные методы анализа и синтеза
СП-моделей сложных систем
Этап 3. Построение тензорных уравнений.
Уравнение изменения разметки СП-модели при срабатывании перехода t
можно записать следующим образом:
µ' = µ + d ,
(1)
где µ - старый вектор разметки СП-модели, µ' - вектор разметки СП-модели
после срабатывания перехода t.
В соответствии с постулатом первого обобщения уравнение (1) можно
представить следующим образом:
µ' = µ + D × f(σ) ,
где f(σ) - степень последовательности срабатывания, представляющая собой
вектор, каждый элемент которого указывает на количество срабатываний
соответствующего перехода СП-модели;
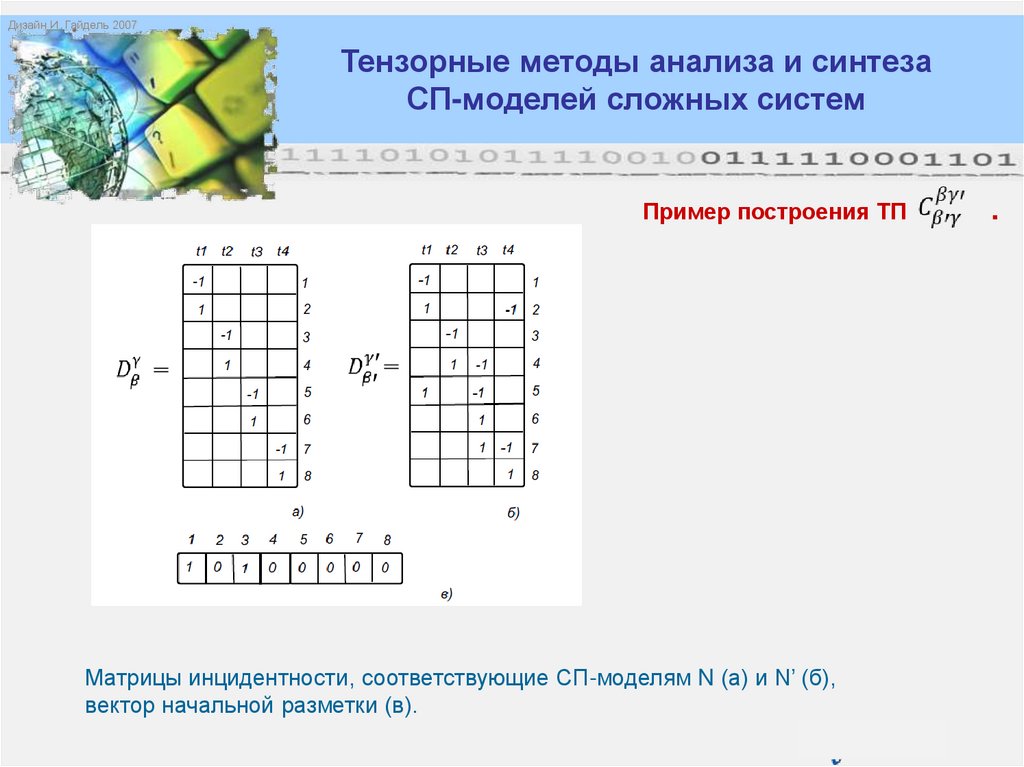
D - матрица инцидентности, составленная из векторов d, построенных для
каждого перехода,
то есть D = О – I , где I: P×T →{0,1,2,..} и O: P×T → {0,1,2,…}.
Примечание: D новое обозначение матрицы С, введенной ранее. Новое обозначение
введено, чтобы не менять общепринятое обозначение тензора C, которое будет
рассмотрено позже..
49.
Дизайн И. Гайдель 2007Методы анализа сетей Петри
= (0,0).
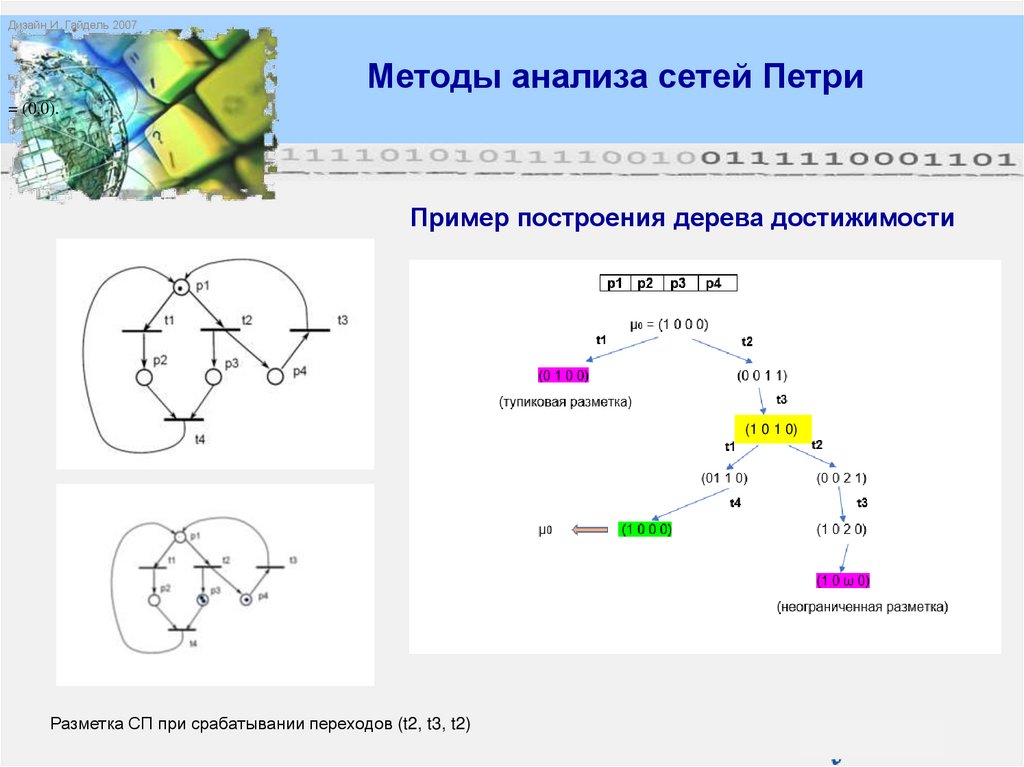
Пример построения дерева достижимости
(1 0 1 0)
Разметка СП при срабатывании перехода t1
50.
Дизайн И. Гайдель 2007Методы анализа сетей Петри
= (0,0).
Пример построения дерева достижимости
(1 0 1 0)
Разметка СП при срабатывании переходов (t2, t3, t2)
51.
Дизайн И. Гайдель 2007Тензорные методы анализа и синтеза
СП-моделей сложных систем
Этап 3. Построение тензорных уравнений.
Если учесть, что СП-структура начинает функционировать от начальной
разметки µ0 , то


































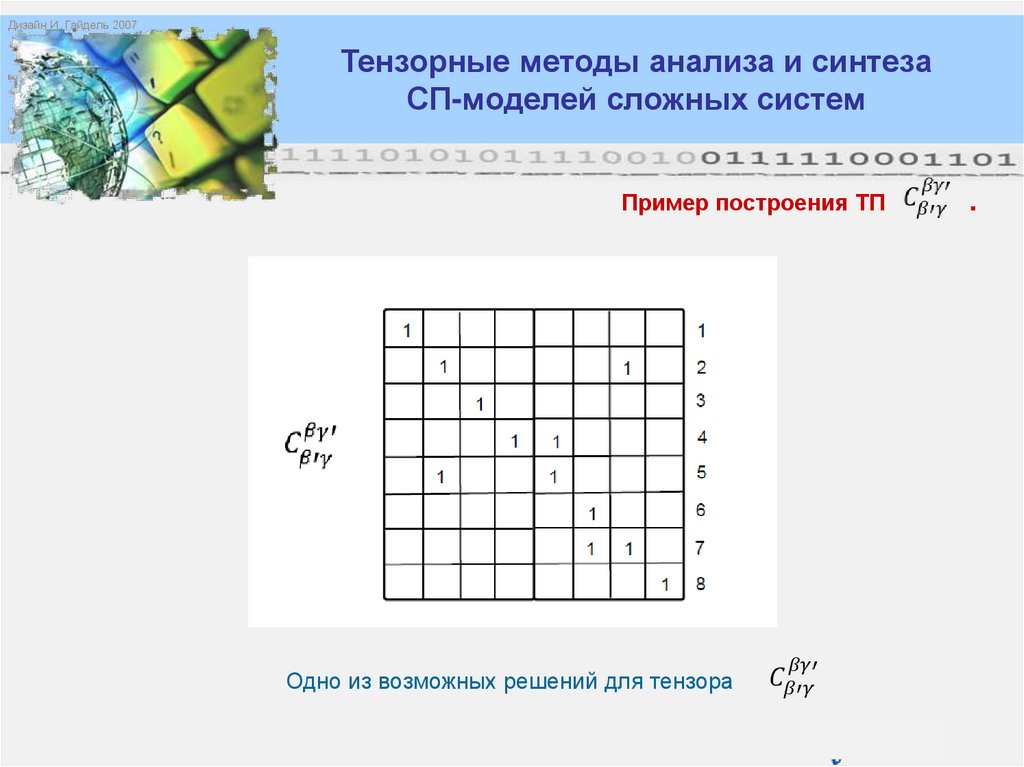
 Математика
Математика








