Похожие презентации:
Системы эконометрических уравнений
1.
2.
3.
4.
BY AX EВ – матрица коэффициентов при зависимых
переменных;
Y – вектор зависимых переменных;
А – матрица коэффициентов при объясняющих
переменных;
Х – вектор объясняющих переменных;
Е – вектор ошибок.
5.
BY AX E6. Система независимых уравнений
СИСТЕМА НЕЗАВИСИМЫХ УРАВНЕНИЙу1 а11 х1 а12 х2 ... а1m x m 1,
у 2 а 21 х1 а 22 х2 ... а 2m хm 2,
у а x a x ... a x
n
n1 1
n2 2
nm m
n.
7.
Система независимых уравненийy1 a01 a11 x1 a12 x2 a13 x3 1
y2 a02 a21 x1 a22 x2 a23 x3 2
y a a x a x a x
3
03
31 1
32 2
33 3
3
1 0 0
B 0 1 0
0 0 1
8.
Система рекурсивных уравнений9.
Система рекурсивных уравненийy1 a01 a11 x1 a12 x2 a13 x3 1
y2 a02 b21 y1 a22 x2 a23 x3 2
y a b y b y a x a x
3
03
31 1
32 2
34 4
35 5
3
y1 производит ельность труда;
y фондоотдача
2
y 3 себестоимо сть продукции
x1 фондовооруженность труда
x 2 энерговооруженность труда
x 3 квалификац ия рабочих
x 4 зарплатоем кость продукции
x материалое мкость продукции
5
1
B b21
b31
0
1
b32
0
0
1
10.
Система взаимозависимых уравненийСистема совместных одновременных переменных / Структурная форма модели
Эндогенные переменные – зависимые переменные,
число которых равно числу уравнений (y)
Экзогенные переменные – предопределенные
переменные, влияющие на эндогенные переменные, но
независящие от них (x)
Лаговые переменные (могут рассматриваться в
качестве экзогенных) – значения эндогенных
переменных за предшествующий период времени
11.
Система взаимозависимых уравненийСистема совместных одновременных переменных / Структурная форма модели
у1 b12 y2 b13 y3 ... b1n yn а11 x1 ... а1m xm 1,
у2 b21 y1 b23 y3 ... b2 n yn а21 х1 ... а2 m xm 2,
уn bn1 y1 bn 2 y2 ... bn, n 1 yn 1 an1 x1 ... anm xm n.
12.
Система взаимозависимых уравненийСистема совместных одновременных переменных / Структурная форма модели
y1 a01 b12 y2 a11 x1 a12 x2 1
y2 a02 b21 y1 b23 y3 a23 x3 2
y a b y a x
3
03
32 2
33 3
3
1
y1 объем продукции;
y производит ельность труда
b
2
B
21
y 3 фондоотдача
0
x1 основные производст венные фонды
x 2 затраты на рабочую силу
x 3 энерговооруженность труда
b12
1
b32
0
b23
1
13.
Приведенная форма моделиyˆ1 11 x1 ... 1m xm,
уˆ 2 21 х1 ... 2 m xm,
yˆ x ... x
n
n1 1
nm m.
• система независимых уравнений
• оценка параметров по МНК
• коэффициенты – нелинейные функции коэффициентов
структурной формы модели
14.
Вычисление коэффициентов приведенной моделиy1 b12 y2 a11 x1 1 ,
y2 b21 y1 a22 x2 2
y1 a11 x1
y2
b12
y1 11 x1 12 x2 u1 ,
y2 21 x1 22 x2 u2 .
y1 a11 x1
b21 y1 a22 x2
b12
a11
a22b12
y1
x1
x2
1 b12b21
1 b12b21
a11b21
a22
y2
x1
x2
1 b12b21
1 b12b21
15.
Вычисление коэффициентов приведенной моделиa11
a22b12
y1 1 b b x1 1 b b x2 ,
12 21
12 21
y a11b21 x a22 x .
2 1 b12b21 1 1 b12b21 2
a11
a22b12
11
, 12
,
1 b12b21
1 b12b21
a11b21
a22
21
, 22
.
1 b12b21
1 b12b21
16.
Идентификация моделиИдентификация – это единственность соответствия
между приведенной и структурной формами модели
Проблема:
m m n 1
m n
Количество параметров структурной формы
модели
Количество параметров приведенной формы
модели
17.
Идентификация модели• идентифицируемые
• неидентифицируемые
• сверхидентифицируемые
18.
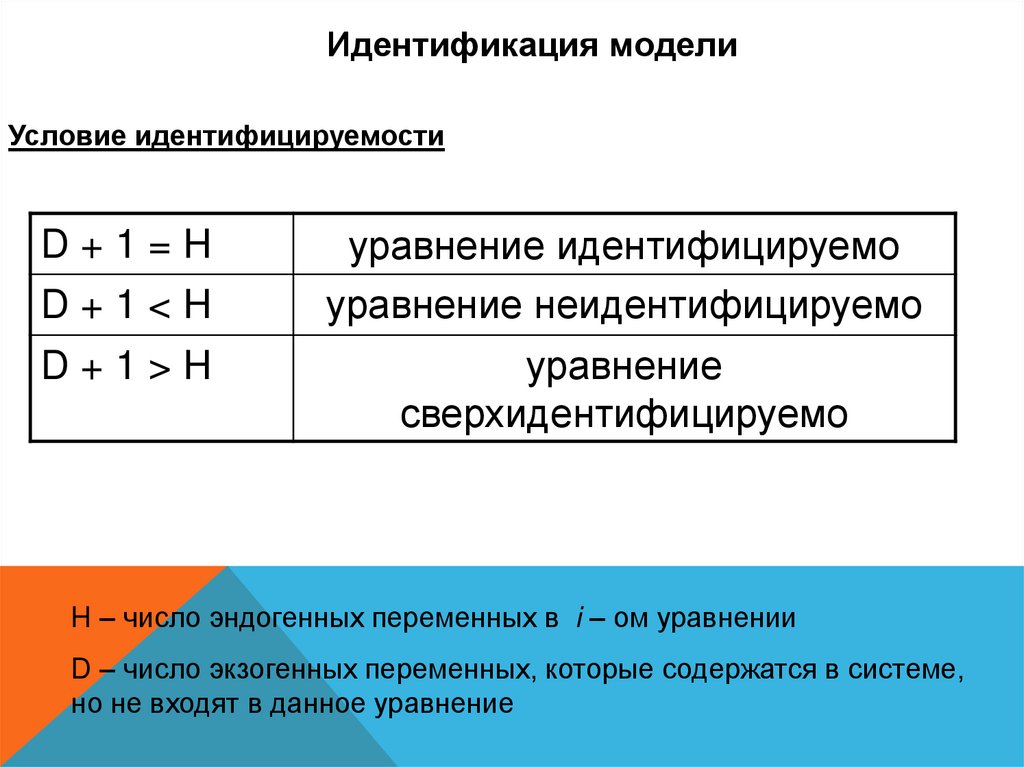
Идентификация моделиУсловие идентифицируемости
D+1=H
D+1<H
D+1>H
уравнение идентифицируемо
уравнение неидентифицируемо
уравнение
сверхидентифицируемо
H – число эндогенных переменных в i – ом уравнении
D – число экзогенных переменных, которые содержатся в системе,
но не входят в данное уравнение
19.
ПРИМЕРCt a1 b11 Yt b12 Ct 1 1 ,
I a b r b I ,
t
2
21
t
22
t 1
2
r
a
b
Y
b
M
,
t
3
31
t
32
t
3
Yt Ct I t Gt ,
20.
Проверка условий идентификацииCt a1 b11 Yt b12 Ct 1 1
H 2
D 4 1 3
D 1 H
21.
Проверка условий идентификацииI t a2 b21 rt b22 I t 1 2
H 2
D 4 1 3
D 1 H
22.
Проверка условий идентификацииrt a3 b31 Yt b32 M t 3
H 2
D 4 1 3
D 1 H
23.
Достаточные условия идентификацииРанг матрицы коэффициентов при
переменных, не входящих в
исследуемое уравнение, должен быть
на единицу меньше числа эндогенных
переменных модели
24.
Достаточные условия идентификацииСt
It
rt
Yt
Ct-1
It-1
Mt
Gt
I уравнение
–1
0
0
b11 b12
0
0
0
II уравнение
0
–1
b21
0
0
b22
0
0
III уравнение
0
0
–1
b31
0
0
b32
0
Тождество
1
1
0
–1
0
0
0
1
25.
Достаточные условия идентификацииIt
rt
It-1
Mt
Gt
II уравнение
–1
b21
b22
0
0
III уравнение
0
–1
0
b32
0
Тождество
1
0
0
0
1
b22 0 0
0 b32 0 b22b32 0
0 0 1
26.
Достаточные условия идентификацииСt
Yt
Ct-1
Mt
I уравнение
–1
b11
b12
0
0
III уравнение
0
b31
0
b32
0
Тождество
1
–1
0
0
1
b12
0
0
0
b32
0
0
0 b12b32 0
1
Gt
27.
Достаточные условия идентификацииСt
It
Ct-1
It-1
Gt
I уравнение
–1
0
b12
0
0
II уравнение
0
1
–1
1
0
0
b22
0
0
1
b12
0
0
0
b22
0
0
0 b12b22 0
1
Тождество
28.
Приведенная форма моделиCt A1 11Ct 1 12 I t 1 13 M t 14Gt u1 ,
I A C I M G u ,
t
2
21 t 1
22 t 1
23
t
24 t
2
rt A3 31Ct 1 32 I t 1 33 M t 34Gt u3 ,
Yt A4 41Ct 1 42 I t 1 43 M t 44Gt u1.



























 Математика
Математика Экономика
Экономика