Транспортная задача

1. ТРАНСПОРТНАЯ ЗАДАЧА

ЛЕКЦИЯ 6
ТРАНСПОРТНАЯ ЗАДАЧА
1

2. Постановка задачи

• Имеется m поставщиков A1 , A2, …, Am и n потребителей B1 ,
B2, …, Bn некоторого груза.
• Для каждого поставщика и потребителя заданы запасы
ai ≥ 0, i = 1, 2, …, m и объем потребления bj ≥ 0, j = 1, 2, …, n.
• Известна стоимость перевозки единицы груза сij ≥ 0 от i-го
поставщика к j-му потребителю.
• Требуется найти объемы всех перевозок xij от i-го поставщика
к j-му потребителю, при которых общая стоимость
минимальна.
2

3. Математическая постановка задачи

Пусть X = (xij) – m×n матрица, где
xij – объем перевозок от i-го поставщика
к j-му потребителю.
Общие затраты на перевозку груза
определяются функцией:
m
n
z ( X ) cij xij
i 1 j 1
3

4.

• Математическая постановка транспортной задачи определяется
задачей линейного программирования:
при условиях
m
n
z ( X ) cij xij min
i 1 j 1
m
x b , j 1,..., n
i 1
ij
j
n
x a , i 1,..., m
j 1
ij
i
xij 0
4

5.

Решение X = (xij) транспортной задачи,
удовлетворяющее условиям и имеющее не
более m+n–1 занятой клетки , будем называть
опорным планом транспортной задачи.
Закрытая модель: суммарные запасы
поставщиков равны суммарным запросам
потребителей, т.е.
m
n
a b
i 1
i
j 1
j
Открытая модель:
m
n
a b
i 1
i
j 1
j
5

6.

Нахождение исходного опорного решения
Клетки, в которые поместим грузы, называются занятыми,
им соответствуют базисные переменные опорного решения.
Остальные клетки незанятые, или пустые, им соответствуют
свободные переменные.
В верхнем правом углу каждой клетки будем записывать тарифы.
Рассмотрим один из способов нахождения исходного опорного
решения — метод минимального тарифа (элемента). Грузы распределяются
в первую очередь в те клетки, в которых находится минимальный тариф
перевозок cij.Далее поставки распределяются в незанятые клетки с
наименьшими тарифами с учетом оставшихся запасов у поставщиков и
удовлетворения спроса потребителей.
Процесс распределения продолжают до тех пор, пока все грузы от
поставщиков не будут вывезены, а потребители не будут удовлетворены.
При распределении грузов может оказаться, что количество занятых клеток
меньше, чем т + п - 1.В этом случае недостающее их число заполняется
клетками с нулевыми поставками, такие клетки называют условно занятыми. Нулевые поставки помещают в незанятые клетки с учетом
наименьшего тарифа таким образом, чтобы в каждых строке и столбце было
не менее, чем по одной занятой клетке.
6

7. Задача 1

Решите транспортную задачу методом потенциалов. В ответе укажите
минимальную стоимость всех перевозок.
B1
B2
B3
B4
ai
A1
1
11
3
13
140
A2
12
4
8
2
160
A3
bj
3
5
14
6
100
80
40
150
130
7

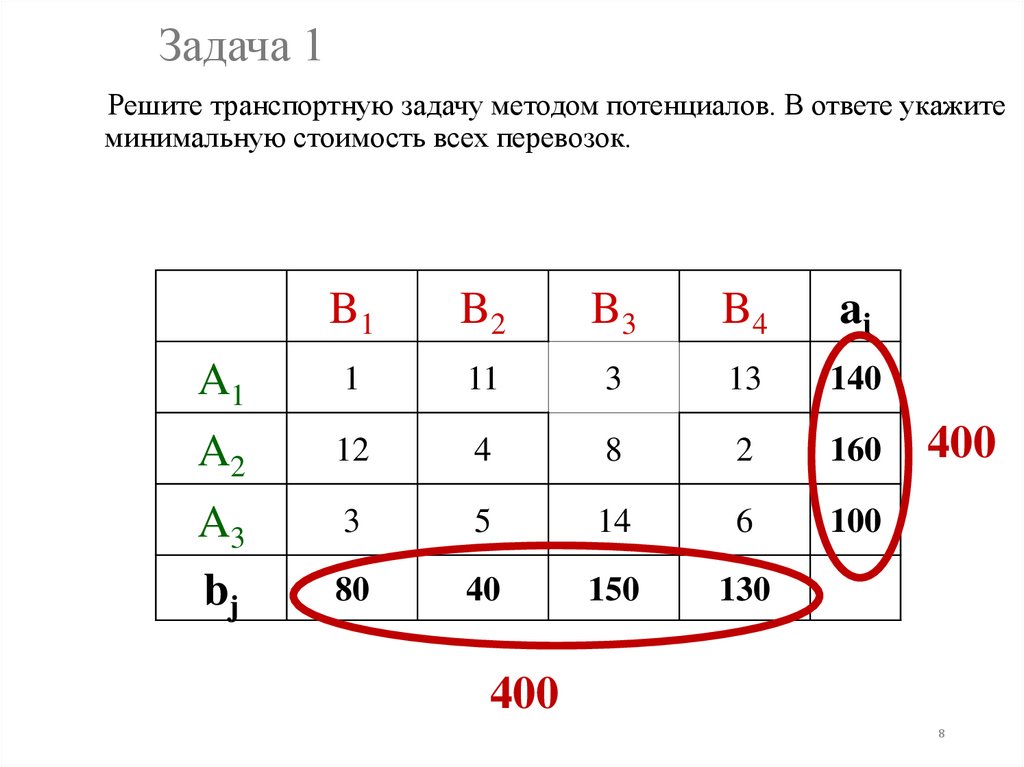
8. Задача 1

Решите транспортную задачу методом потенциалов. В ответе укажите
минимальную стоимость всех перевозок.
B1
B2
B3
B4
ai
A1
1
11
3
13
140
A2
12
4
8
2
160
A3
bj
3
5
14
6
100
80
40
150
130
400
400
8

9. Задача 1

Решите транспортную задачу методом потенциалов. В ответе укажите
минимальную стоимость всех перевозок.
Дана закрытая транспортная задача.
B1
B2
B3
B4
ai
A1
1
11
3
13
140
A2
12
4
8
2
160
A3
bj
3
5
14
6
100
80
40
150
130
400
400
400
9

10.

Метод наименьшей стоимости
B1
A1
B3
B4
ai
1
11
3
13
12
4
8
2
3
5
14
6
80
A2
A3
bj
B2
80
40
150
140
160
100
130
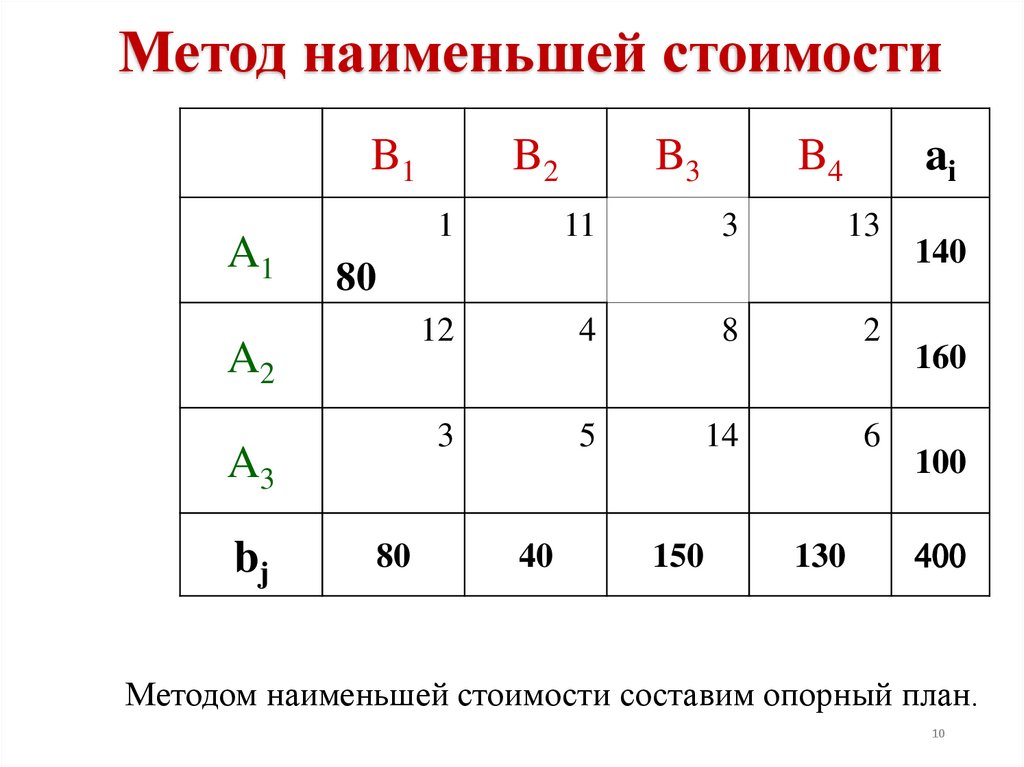
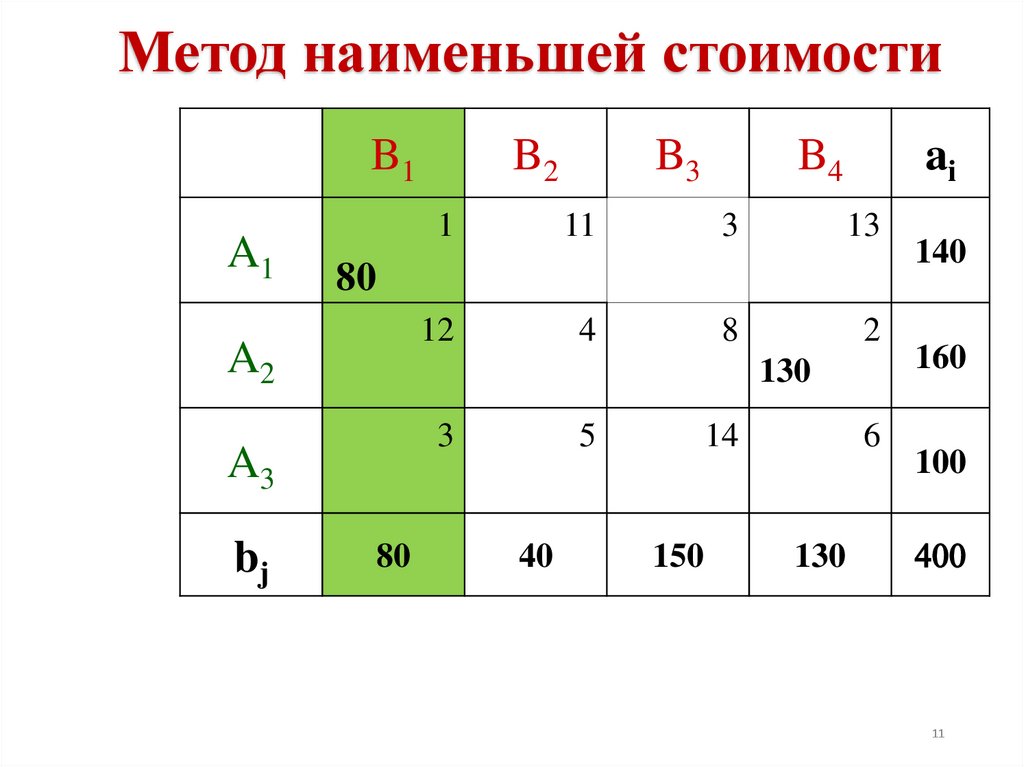
Методом наименьшей стоимости составим опорный план.
10

11.

Метод наименьшей стоимости
B1
A1
B3
B4
ai
1
11
3
13
12
4
8
2
80
A2
130
3
A3
bj
B2
80
5
40
14
150
6
140
160
100
130
11

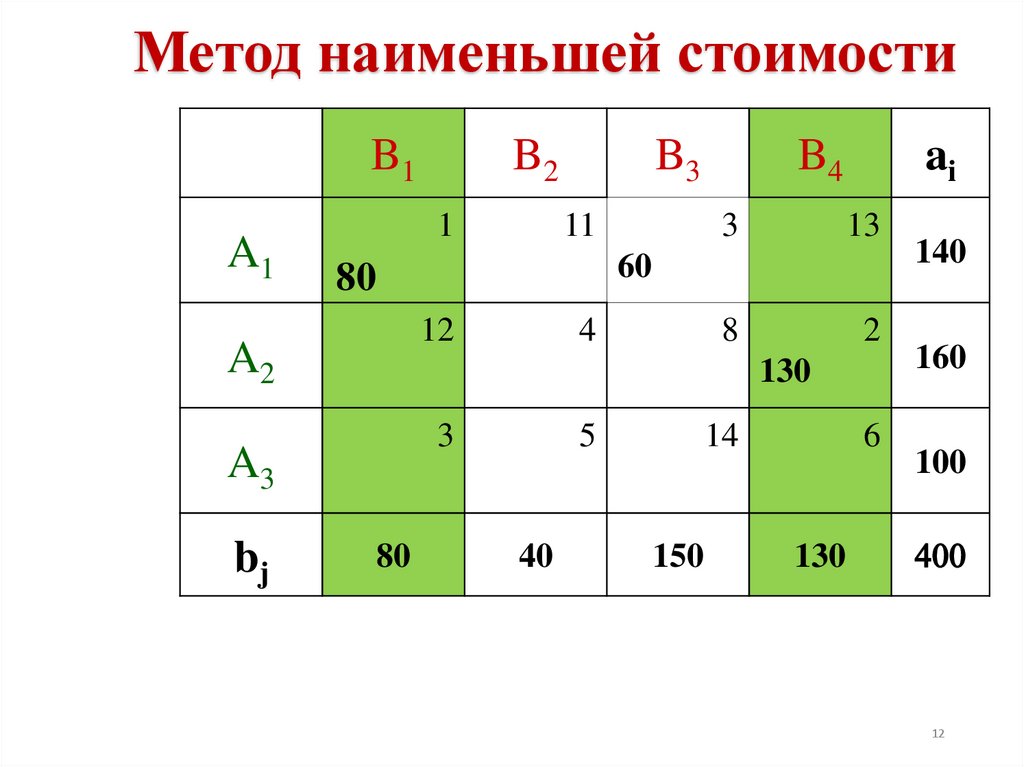
12.

Метод наименьшей стоимости
B1
A1
1
B3
11
B4
ai
3
13
8
2
60
80
12
A2
4
130
3
A3
bj
B2
80
5
40
14
150
6
140
160
100
130
12

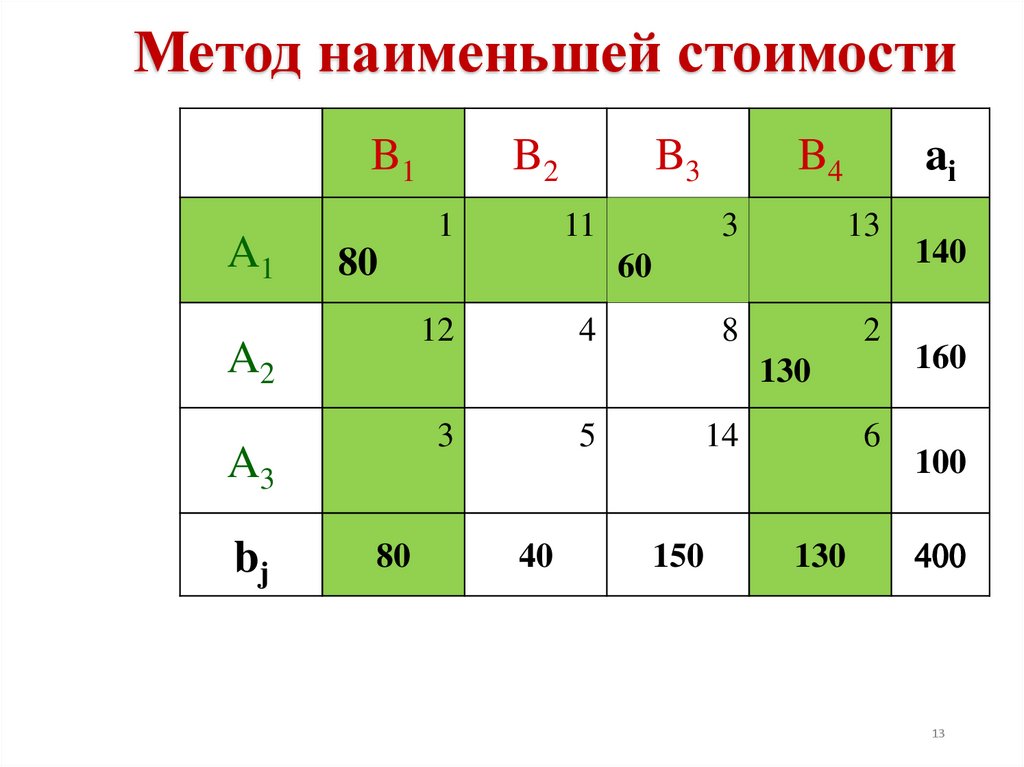
13.

Метод наименьшей стоимости
B1
A1
1
B3
11
80
B4
ai
3
13
8
2
60
12
A2
4
130
3
A3
bj
B2
80
5
40
14
150
6
140
160
100
130
13

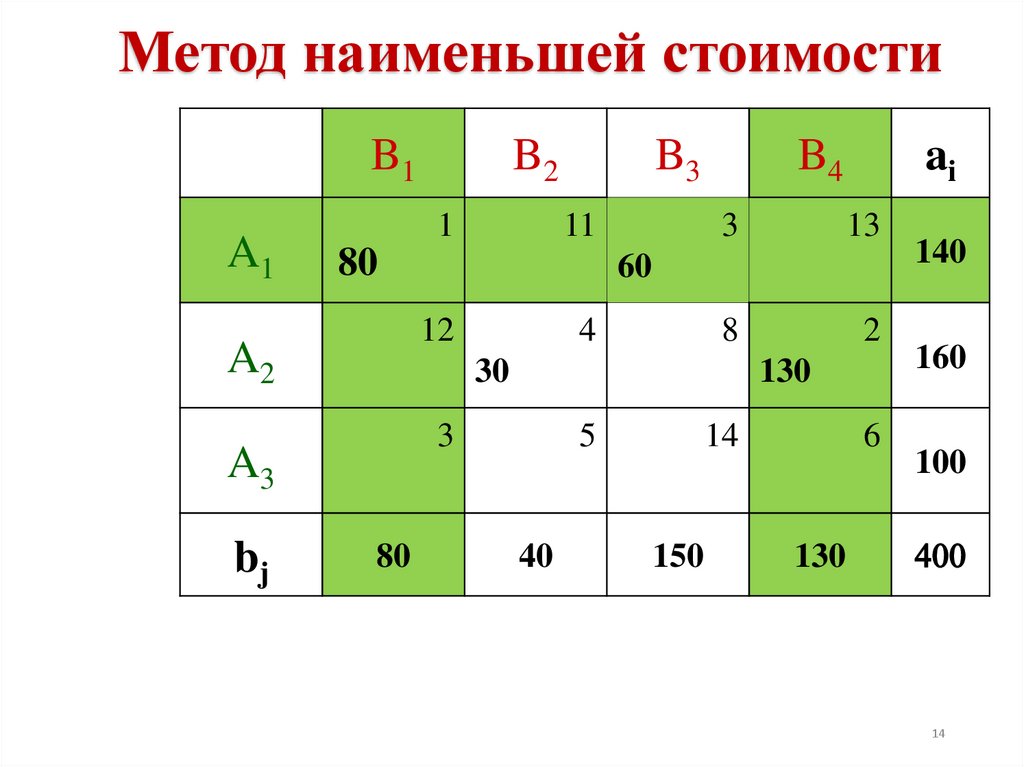
14.

Метод наименьшей стоимости
B1
A1
1
B3
11
80
B4
3
13
4
8
2
30
130
3
A3
80
ai
60
12
A2
bj
B2
5
40
14
150
6
140
160
100
130
14

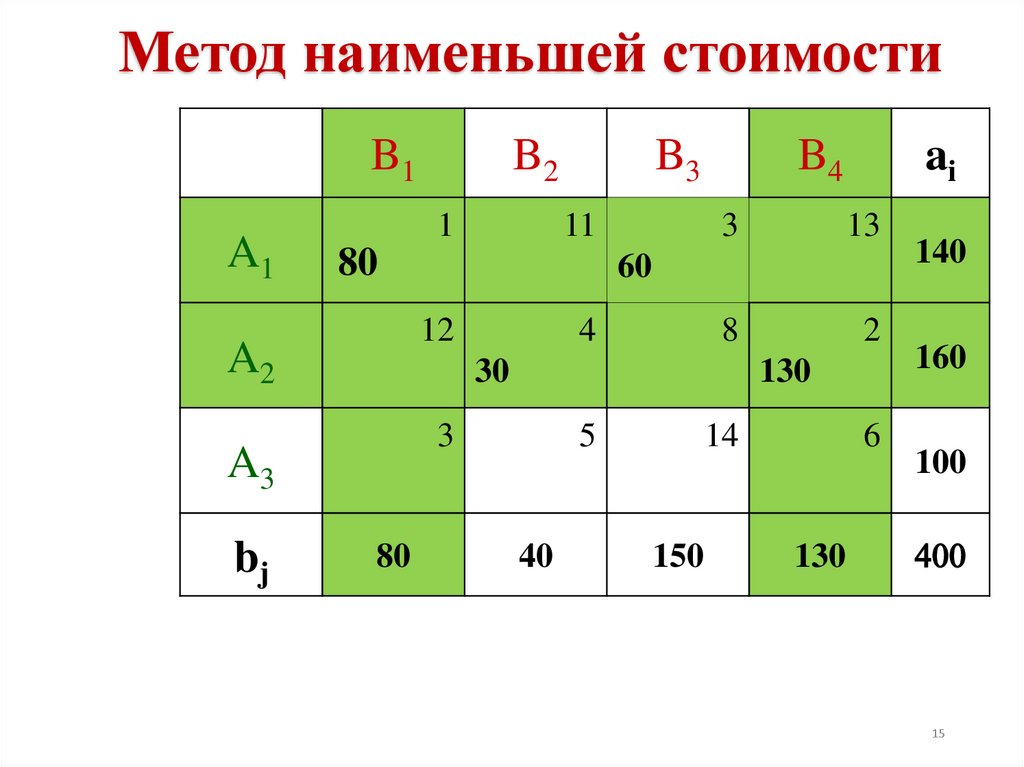
15.

Метод наименьшей стоимости
B1
A1
1
B3
11
80
B4
3
13
4
8
2
30
130
3
A3
80
ai
60
12
A2
bj
B2
5
40
14
150
6
140
160
100
130
15

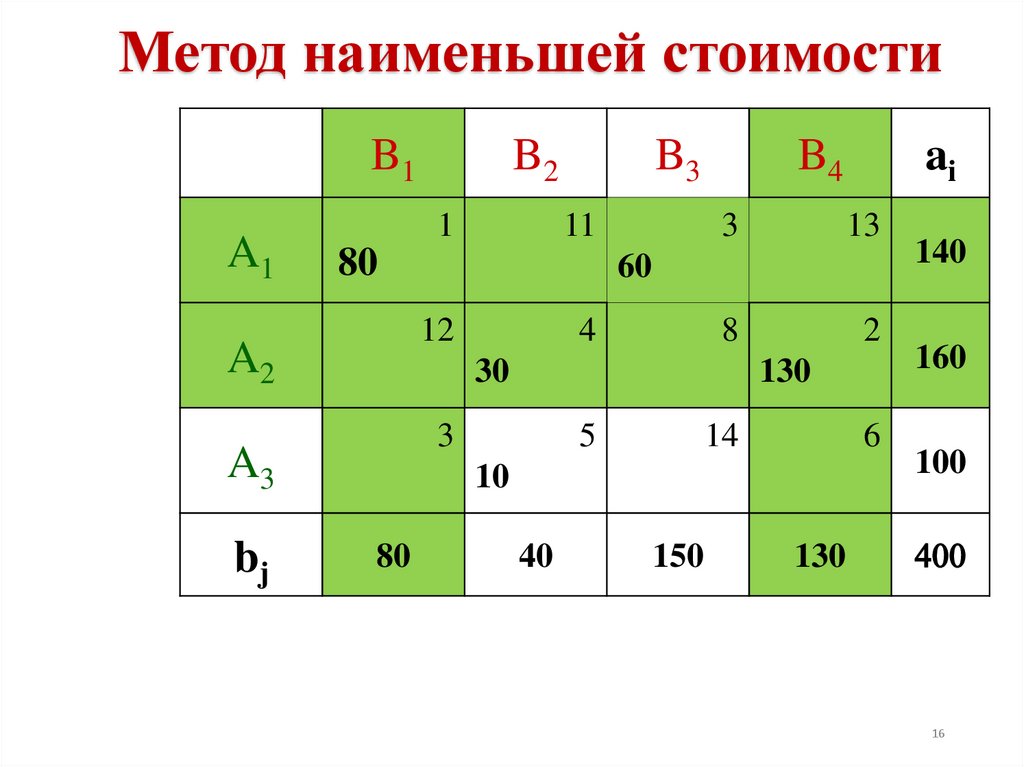
16.

Метод наименьшей стоимости
B1
A1
1
B3
11
80
B4
3
13
4
8
2
30
130
3
A3
5
14
6
10
80
ai
60
12
A2
bj
B2
40
150
140
160
100
130
16

17.

Метод наименьшей стоимости
B1
A1
1
B3
11
80
B4
3
13
4
8
2
30
130
3
A3
5
14
6
10
80
ai
60
12
A2
bj
B2
40
150
140
160
100
130
17

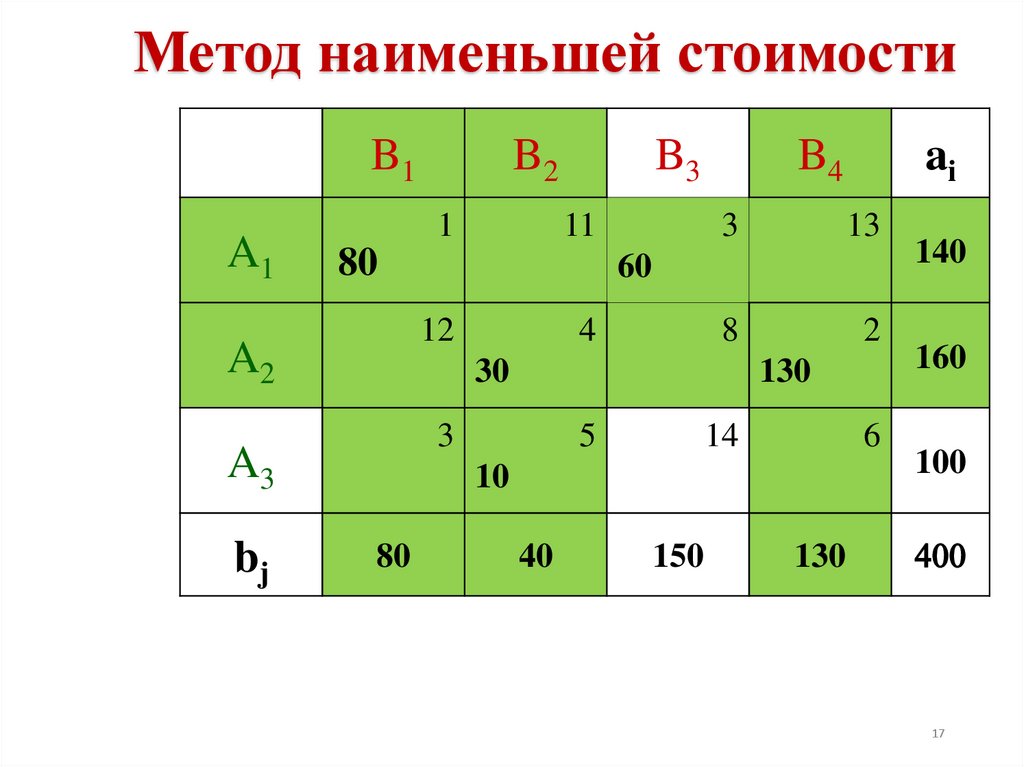
18.

Метод наименьшей стоимости
B1
A1
1
B3
11
80
B4
3
13
4
8
2
30
130
3
A3
5
10
80
ai
60
12
A2
bj
B2
14
6
90
40
150
140
160
100
130
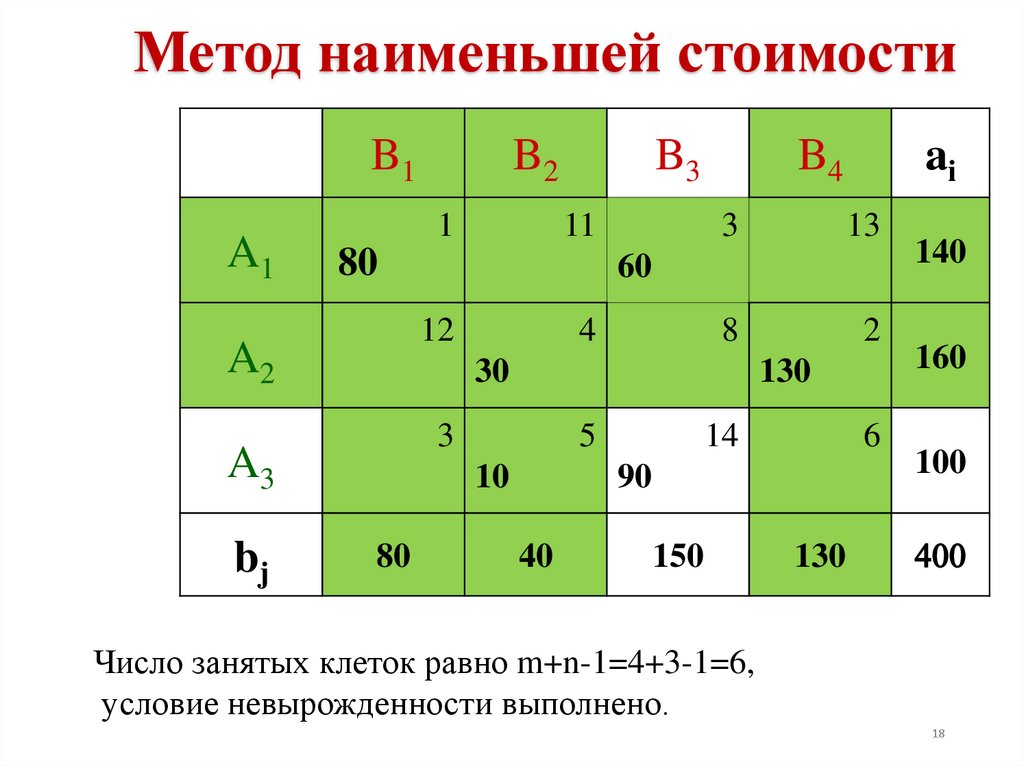
Число занятых клеток равно m+n-1=4+3-1=6,
условие невырожденности выполнено.
18

19.

Метод наименьшей стоимости
B1
A1
1
B3
11
80
B4
ai
3
13
8
2
60
12
A2
4
30
130
3
A3
bj
B2
5
10
80
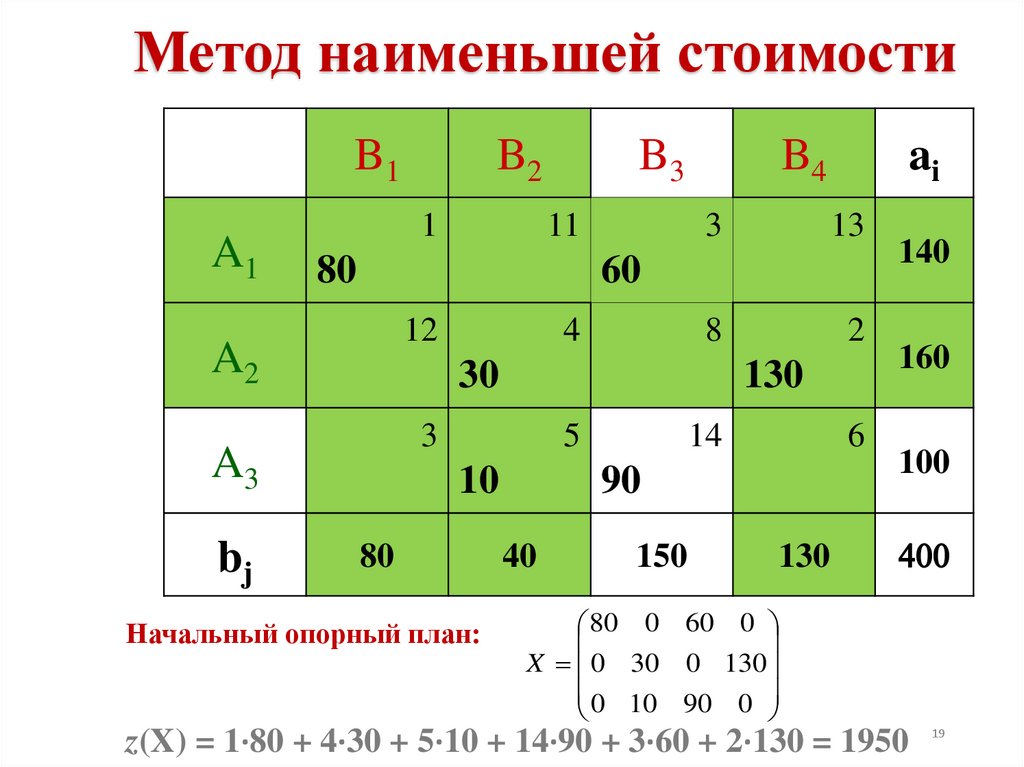
Начальный опорный план:
14
6
90
40
150
140
160
100
130
80 0 60 0
X 0 30 0 130
0 10 90 0
z(X) = 1·80 + 4·30 + 5·10 + 14·90 + 3·60 + 2·130 = 1950
19

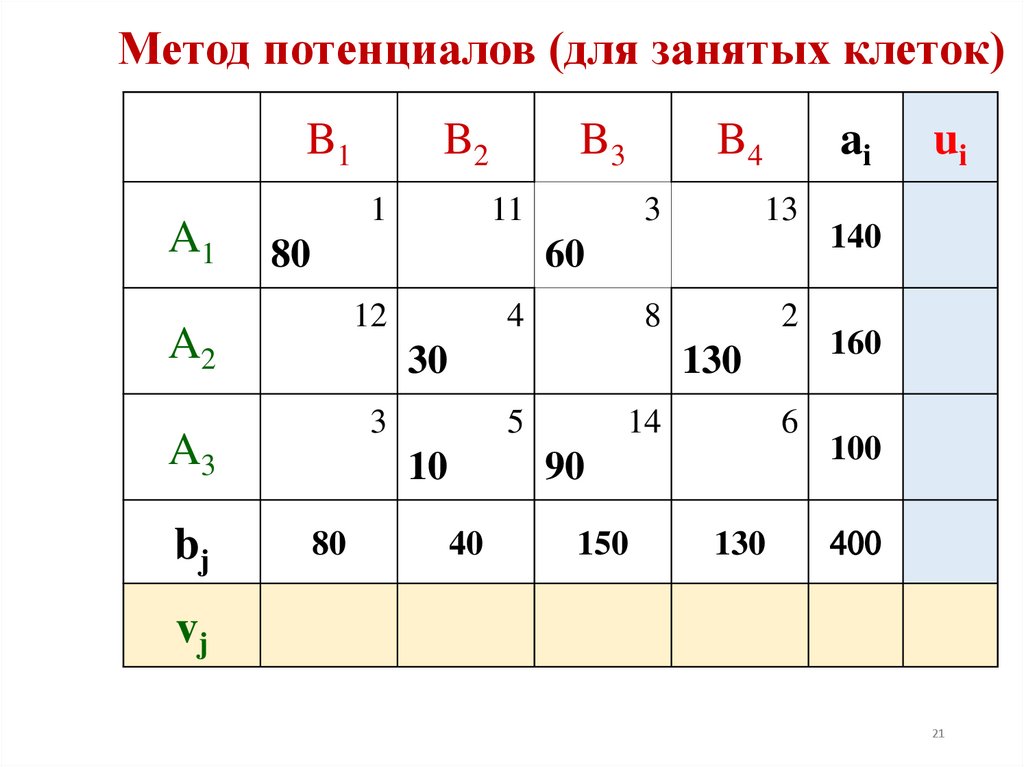
20. Проверка найденного опорного решения на оптимальность методом потенциалов

• Теорема
Если опорный план X = (xij) транспортной задачи является
оптимальным, то существуют потенциалы поставщиков ui,
i = 1,…, m и потребителей vj, j = 1,…, n, удовлетворяющие
условиям:
ui + vj = сij при xij > 0 (для занятых клеток).
Одному из потенциалов дается произвольное значение, например и1 = 0,
тогда остальные потенциалы определяются однозначно. Так, если
известен потенциал ui, то vj = сij — ui; если известен потенциал vj, то ui =
cij – vj.
Δij = ui + vj - сij ≤ 0 при xij = 0 (для свободных клеток).
20

21. Метод потенциалов (для занятых клеток)

B1
A1
1
B3
B4
11
80
ai
3
13
8
2
60
12
A2
4
30
130
3
A3
bj
B2
5
10
80
14
6
90
40
150
ui
140
160
100
130
vj
21

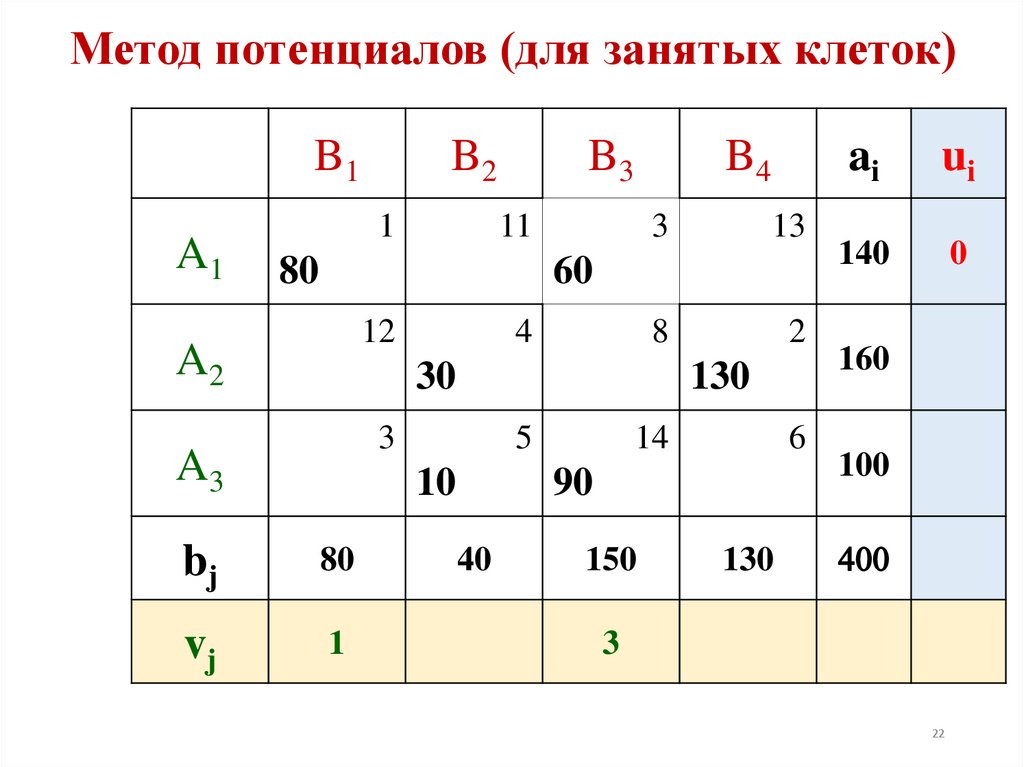
22. Метод потенциалов (для занятых клеток)

B1
A1
B2
1
B3
B4
11
80
3
13
8
2
60
12
A2
4
30
130
3
A3
5
10
bj
80
vj
1
14
6
90
40
150
ai
ui
140
0
160
100
130
3
22

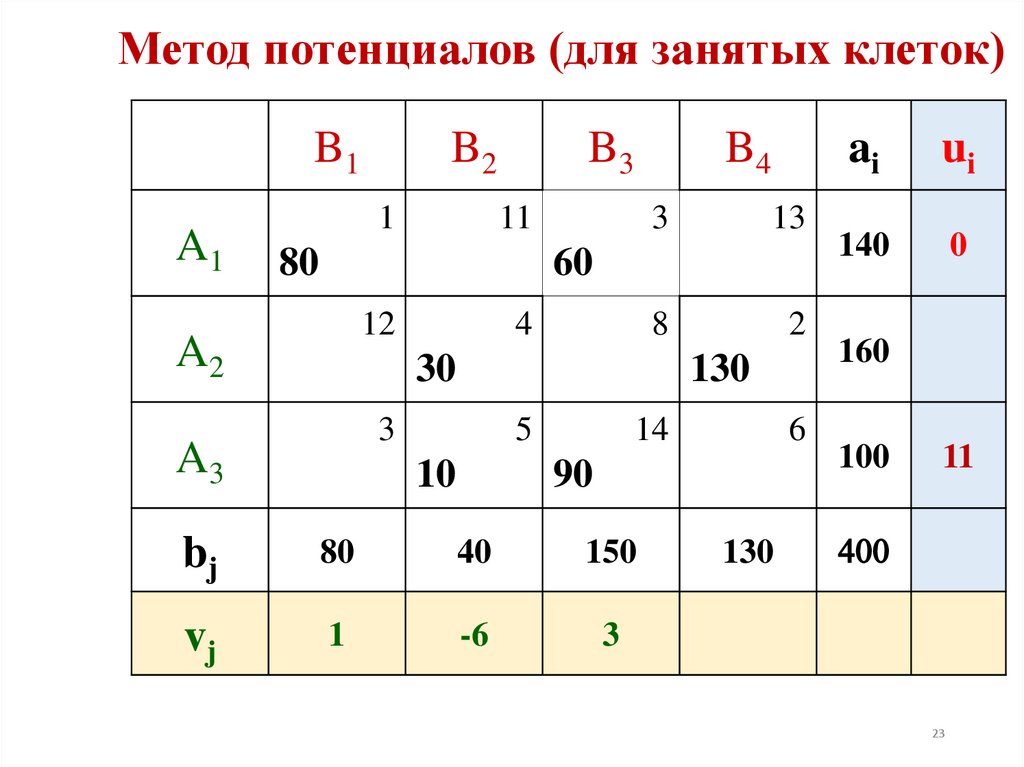
23. Метод потенциалов (для занятых клеток)

B1
A1
B2
1
B3
B4
11
80
3
13
8
2
60
12
A2
4
30
130
3
A3
5
10
14
6
90
bj
80
40
150
vj
1
-6
3
ai
ui
140
0
160
100
11
130
23

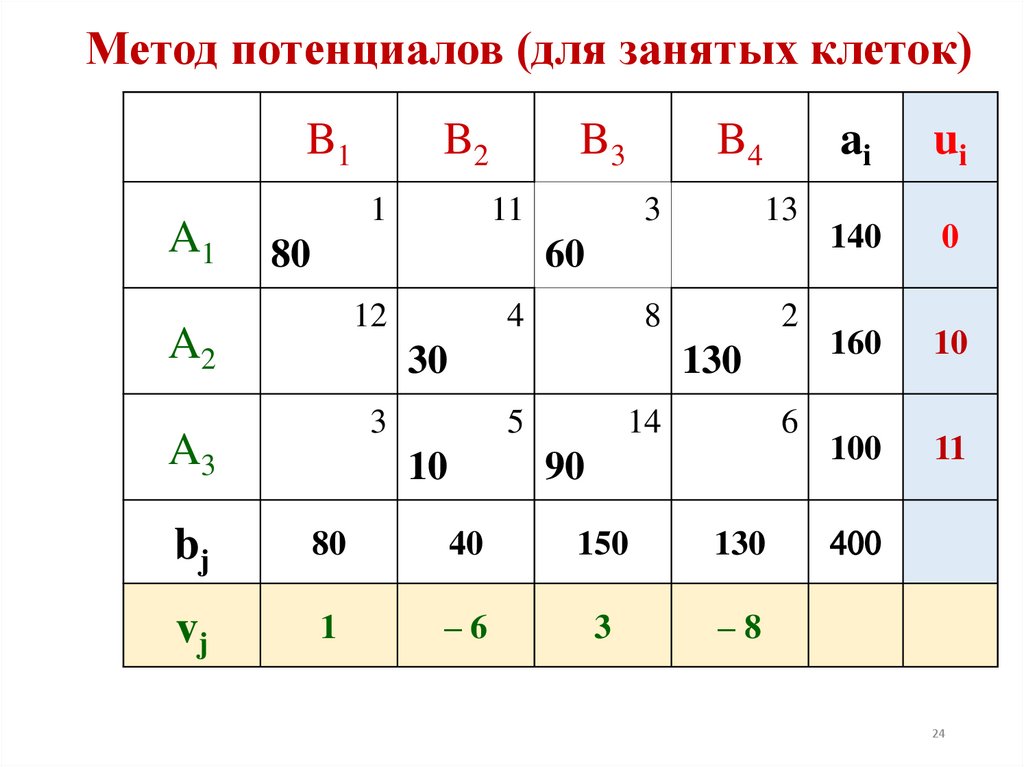
24. Метод потенциалов (для занятых клеток)

B1
A1
B2
1
B3
B4
11
80
3
13
8
2
60
12
A2
4
30
130
3
A3
5
10
14
6
90
bj
80
40
150
130
vj
1
–6
3
–8
ai
ui
140
0
160
10
100
11
24

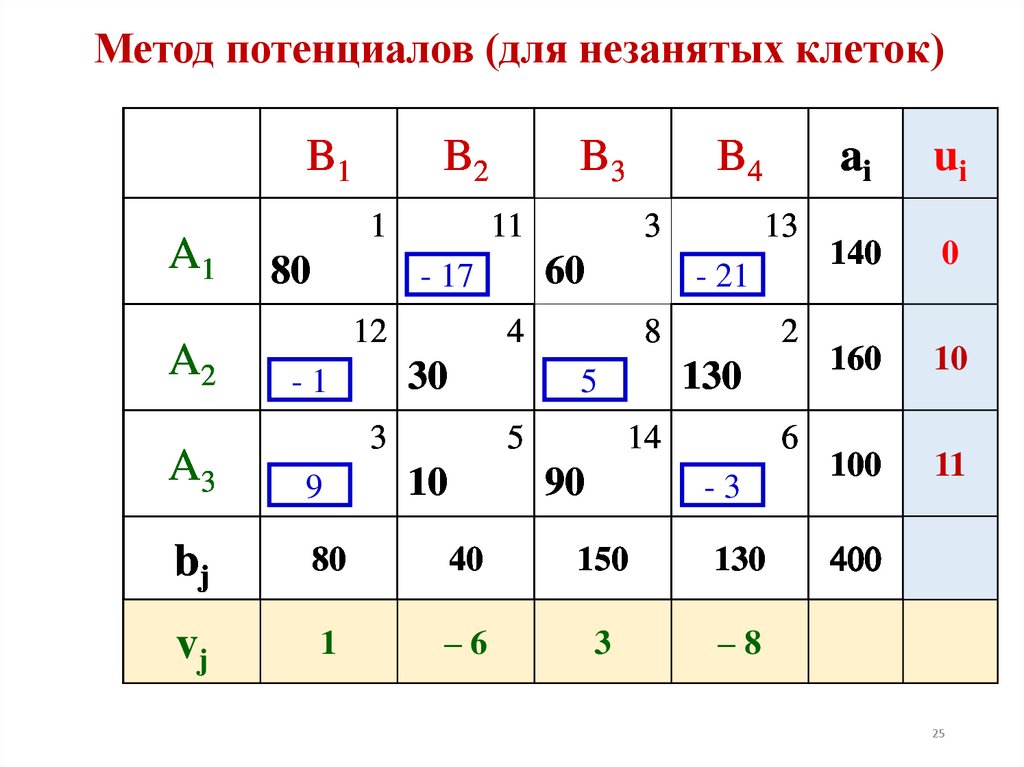
25. Метод потенциалов (для незанятых клеток)

B1
A1
A2
B2
1
80
B3
11
12
3
60
- 17
8
5
2
130
5
3
13
- 21
4
30
-1
B4
14
6
A3
9
bj
80
40
150
130
vj
1
–6
3
–8
10
90
-3
ai
ui
140
0
160
10
100
11
25

26. Метод потенциалов

B1
A1
A2
B2
1
80
B3
11
12
3
60
- 17
8
5
2
130
5
3
13
- 21
4
30
-1
B4
14
6
A3
9
bj
80
40
150
130
vj
1
–6
3
–8
10
90
-3
ai
ui
140
0
160
10
100
11
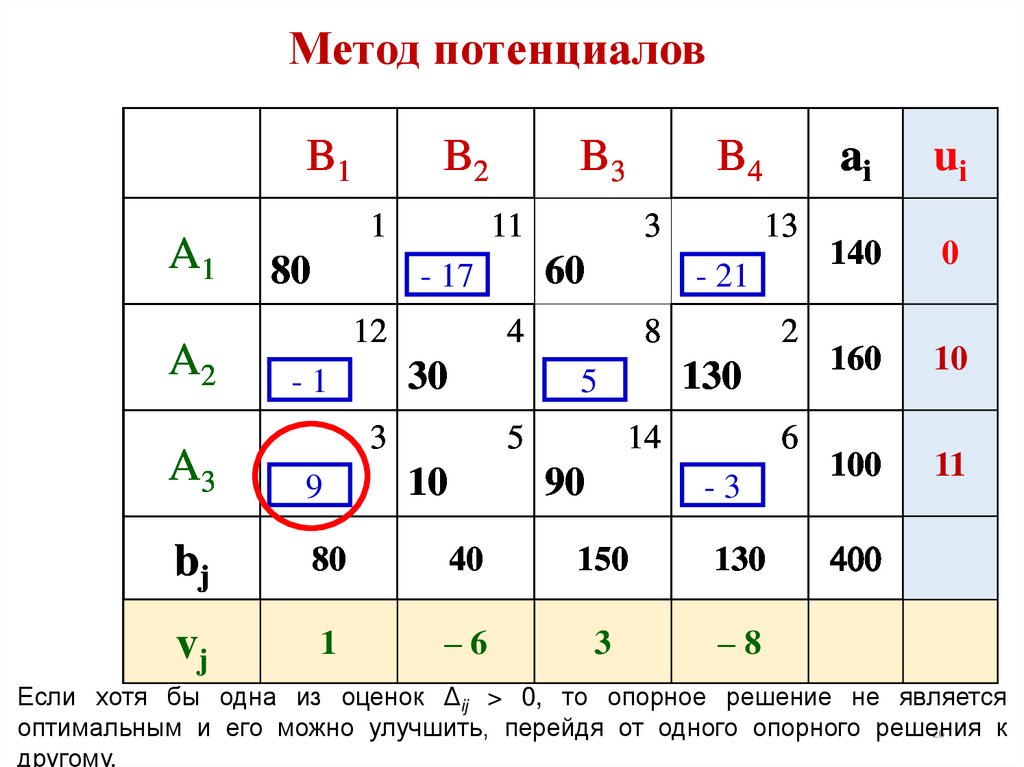
Если хотя бы одна из оценок Δij > 0, то опорное решение не является
оптимальным и его можно улучшить, перейдя от одного опорного решения
к
26
другому.

27.

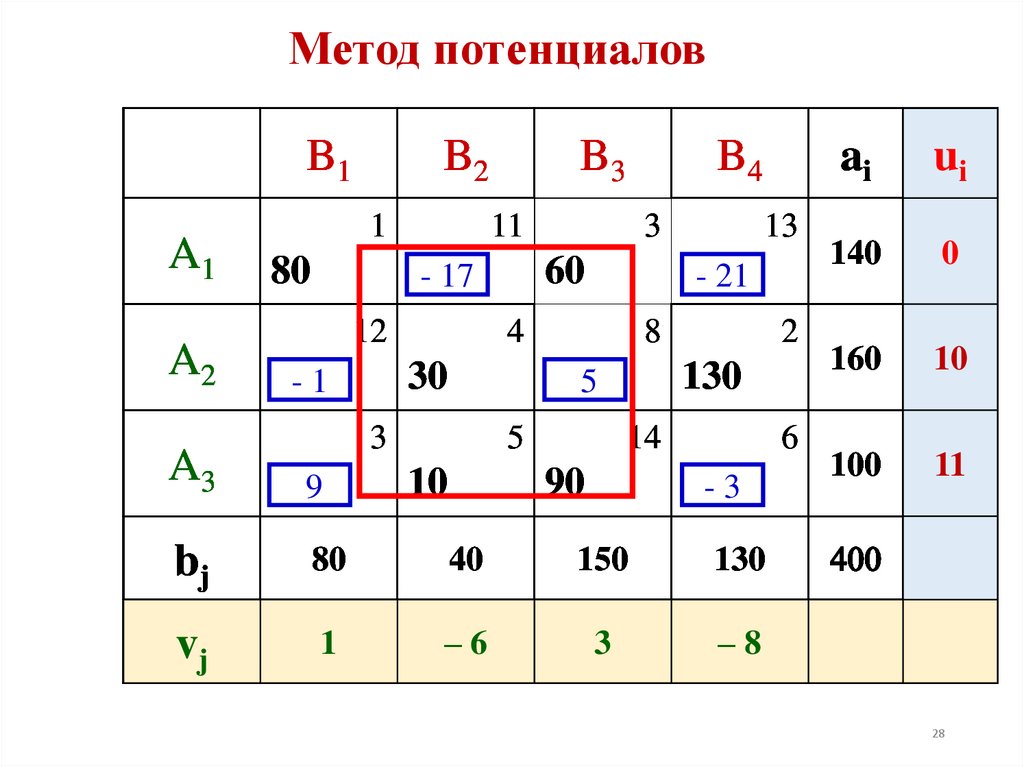
Переход от одного опорного решения к другому
Для свободной клетки с Δij > 0 строится цикл (цепь,
многоугольник), все вершины которого кроме одной
находятся в занятых клетках; углы прямые, число вершин
четное.
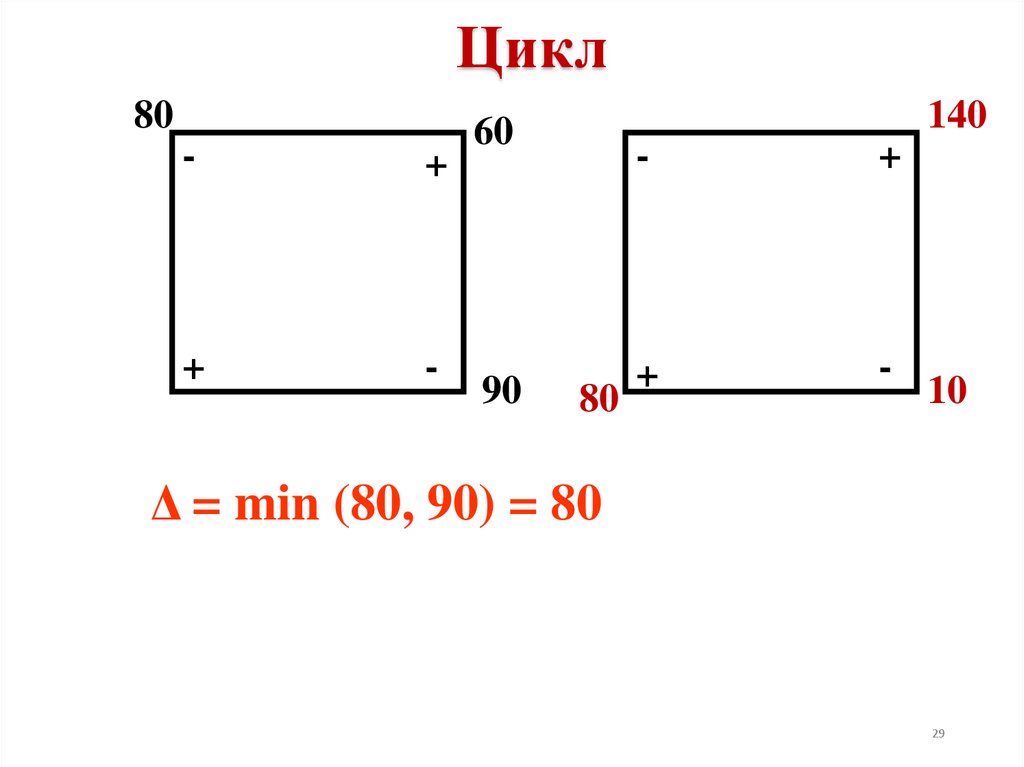
Около свободной клетки цикла ставится знак (+),
затем поочередно проставляют знаки (—) и (+). У вершин
со знаком (—) выбирают минимальный груз, его
прибавляют к грузам, стоящим у вершин со знаком (+), и
отнимают от грузов у вершин со знаком (—).
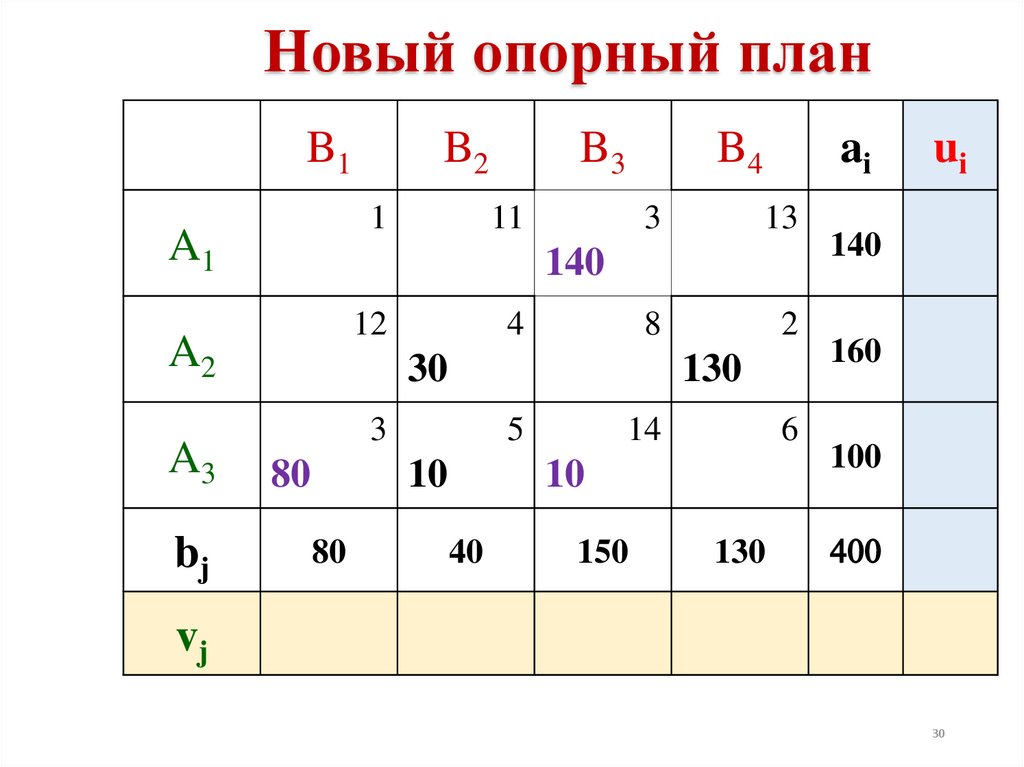
В результате перераспределения груза получим
новое опорное решение. Это решение проверяем на
оптимальность, и т.д. до тех пор, пока не получим
оптимальное решение.
27

28. Метод потенциалов

B1
A1
A2
B2
1
80
B3
11
12
3
60
- 17
8
5
2
130
5
3
13
- 21
4
30
-1
B4
14
6
A3
9
bj
80
40
150
130
vj
1
–6
3
–8
10
90
-3
ai
ui
140
0
160
10
100
11
28

29.

Цикл
80
-
+
+
-
140
60
90
80
-
+
+
-
10
Δ = min (80, 90) = 80
29

30.

Новый опорный план
B1
1
A1
bj
B3
B4
11
ai
3
13
8
2
140
12
A2
A3
B2
4
30
130
3
80
5
10
80
14
6
10
40
150
ui
140
160
100
130
vj
30

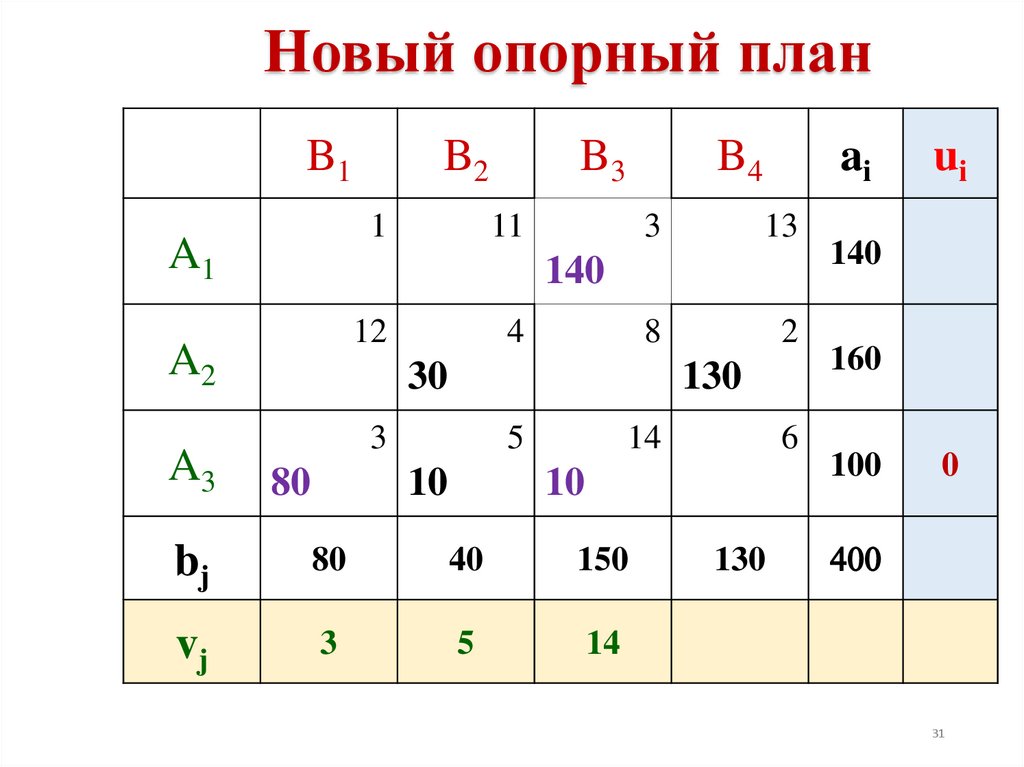
31.

Новый опорный план
B1
1
A1
B3
B4
11
ai
3
13
8
2
140
12
A2
A3
B2
4
30
130
3
80
5
10
14
6
10
bj
80
40
150
vj
3
5
14
ui
140
160
100
0
130
31

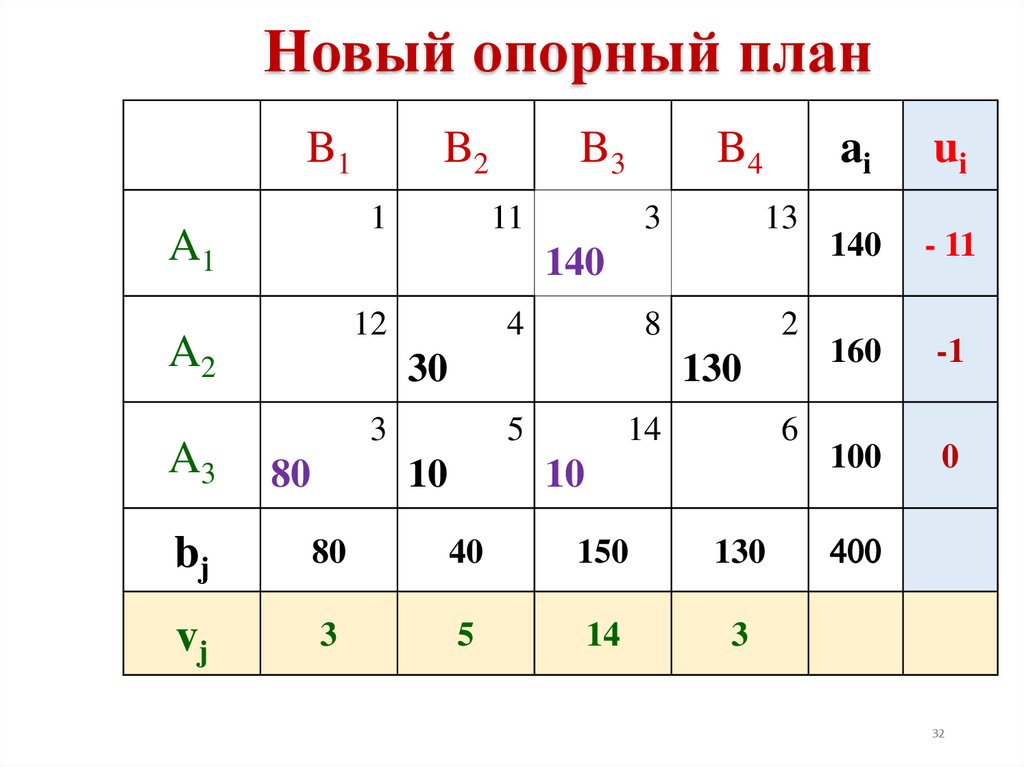
32.

Новый опорный план
B1
1
A1
B3
B4
11
3
13
8
2
140
12
A2
A3
B2
4
30
130
3
80
5
10
14
6
10
bj
80
40
150
130
vj
3
5
14
3
ai
ui
140
- 11
160
-1
100
0
32

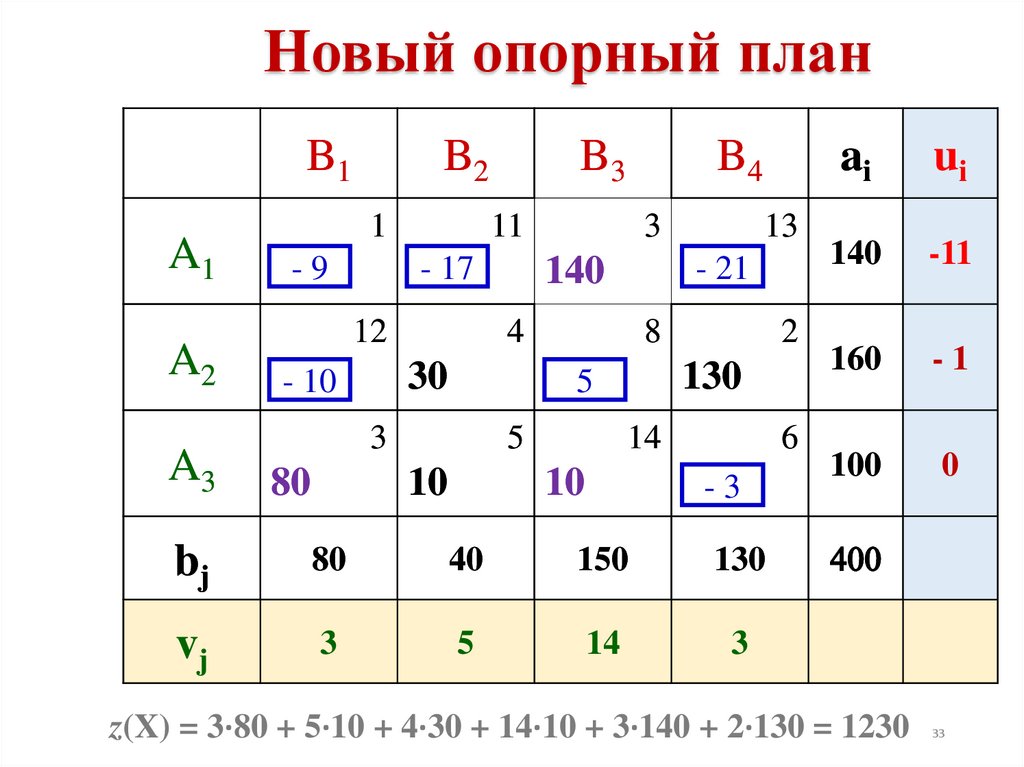
33.

Новый опорный план
B1
A1
A2
A3
B2
1
-9
- 17
3
4
8
5
10
2
130
5
3
13
- 21
140
30
- 10
B4
11
12
80
B3
14
10
6
-3
bj
80
40
150
130
vj
3
5
14
3
ai
ui
140
-11
160
-1
100
0
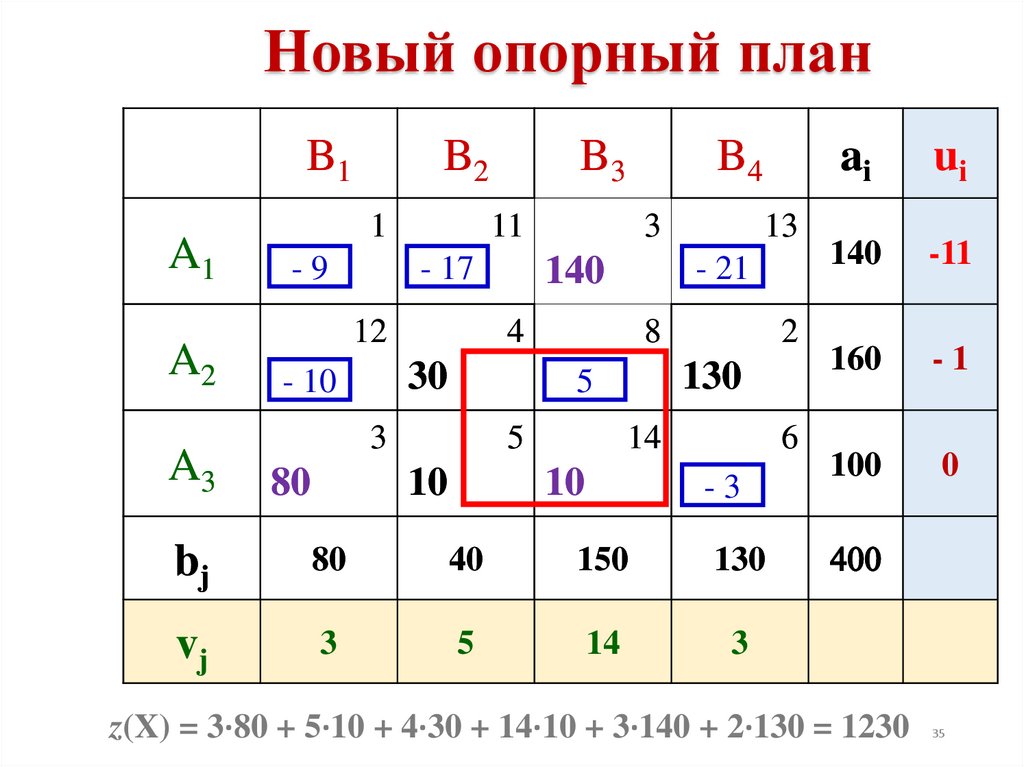
z(X) = 3·80 + 5·10 + 4·30 + 14·10 + 3·140 + 2·130 = 1230
33

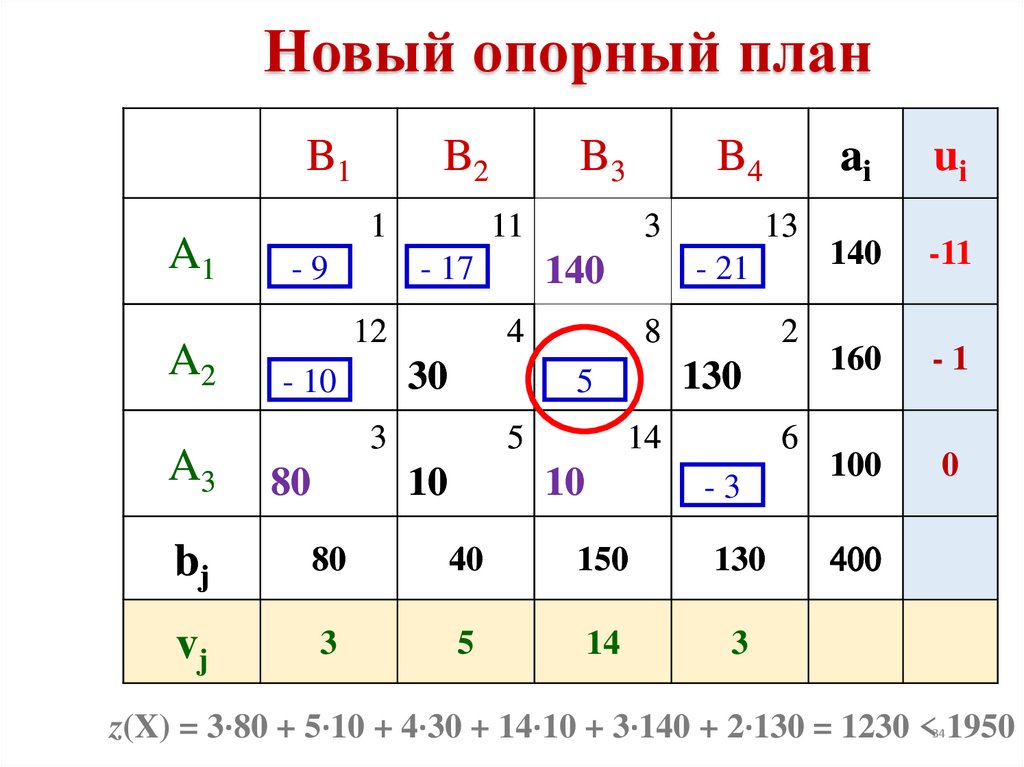
34.

Новый опорный план
B1
A1
A2
A3
B2
1
-9
- 17
3
4
8
5
10
2
130
5
3
13
- 21
140
30
- 10
B4
11
12
80
B3
14
10
6
-3
bj
80
40
150
130
vj
3
5
14
3
ai
ui
140
-11
160
-1
100
0
z(X) = 3·80 + 5·10 + 4·30 + 14·10 + 3·140 + 2·130 = 1230 < 1950
34

35.

Новый опорный план
B1
A1
A2
A3
B2
1
-9
- 17
3
4
8
5
10
2
130
5
3
13
- 21
140
30
- 10
B4
11
12
80
B3
14
10
6
-3
bj
80
40
150
130
vj
3
5
14
3
ai
ui
140
-11
160
-1
100
0
z(X) = 3·80 + 5·10 + 4·30 + 14·10 + 3·140 + 2·130 = 1230
35

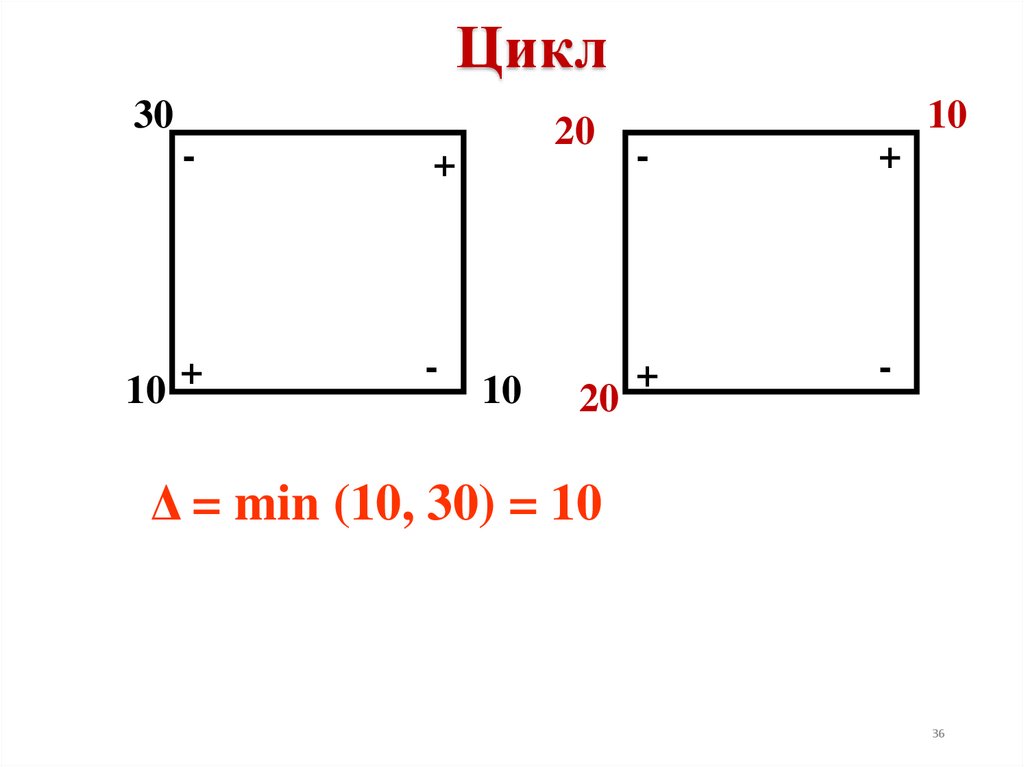
36.

Цикл
30
-
+
10 +
-
20
10
20
10
-
+
+
-
Δ = min (10, 30) = 10
36

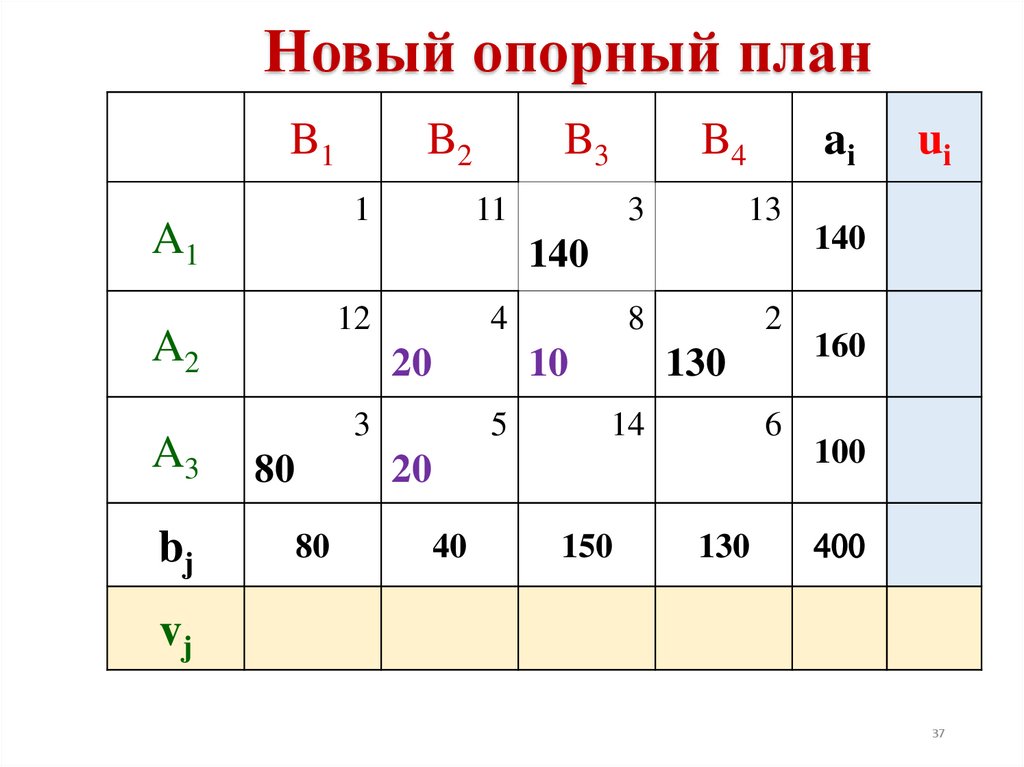
37.

Новый опорный план
B1
1
A1
bj
B3
B4
11
ai
3
13
8
2
140
12
A2
A3
B2
4
20
10
3
80
5
130
14
6
20
80
40
150
ui
140
160
100
130
vj
37

38.

Новый опорный план
B1
A1
A2
A3
B2
1
-4
- 12
3
140
8
10
3
2
130
5
20
13
- 16
4
20
- 10
B4
11
12
80
B3
14
6
-5
-3
bj
80
40
150
130
vj
2
4
8
2
ai
ui
140
-5
160
0
100
1
z(X) = 3·80 + 5·20 + 4·20 + 8·10 + 3·140 + 2·130 = 1180 < 1230
38

39.

Новый опорный план
B1
B2
1
B3
11
B4
3
13
ai
ui
140
-5
A1
-4
A2
8
2
План
160
20
10
130
- 10
оптимален!
3
5
14
6
A3
- 12
12
80
140
- 16
4
20
-5
-3
bj
80
40
150
130
vj
2
4
8
2
100
z(X) = 3·80 + 5·20 + 4·20 + 8·10 + 3·140 + 2·130 = 1180
0
1
39