Похожие презентации:
Синус и косинус суммы и разности аргументов
1. Синус и косинус суммы и разности аргументов
СИНУС И КОСИНУС СУММЫ ИРАЗНОСТИ АРГУМЕНТОВ
2.
Найдите значениеsin 75
0
?
Ответить на данный
вопрос помогут
формулы синуса,
косинуса, тангенса
суммы и разности
аргументов
3.
Формулы синуса и косинуса суммы аргументовsin x y sin x cos y cos x sin y
cos x y cos x cos y sin x sin y
Синус суммы двух аргументов равен произведению
синуса первого аргумента на косинус второго плюс
произведение косинуса первого аргумента на синус
второго
Косинус суммы двух аргументов равен
произведению косинусов этих аргументов минус
произведение синусов этих аргументов
На основании данных формул будут выведены
практически все остальные формулы тригонометрии
4.
Выведем формулу синуса разности двух аргументовsin x y sin x ( y)
sin x cos( y ) cos x sin( y )
Учитывая, что
sin( у ) sin y
cos( у ) cos y
получим,
sin x cos y cos x sin y
5.
sin x y sin x cos y cos x sin yСинус разности двух аргументов равен произведению
синуса первого аргумента на косинус второго минус
произведение косинуса первого аргумента на синус
второго
6.
Аналогично выведем формулу косинуса разностидвух аргументов
cos x y cos x ( y)
cos x cos( y ) sin x sin( y )
cos x cos y sin x sin y
7.
cos x y cos x cos y sin x sin yКосинус разности двух аргументов равен
произведению косинусов этих аргументов плюс
произведение синусов этих аргументов.
8.
Пример 1sin 75
0
Вычислить:
sin( 45 30 )
0
0
sin 45 cos 30 cos 45 sin 30
0
0
2 3
2 1
2 2
2 2
6
2
6 2
4
4
4
0
0
9.
Пример 2 Вычислить:cos 75 cos(45 30 )
0
0
0
cos 45 cos 30 sin 45 sin 30
0
0
2 3
2 1
2 2
2 2
6
2
6 2
4
4
4
0
0
10.
Пример 3 Вычислить:4
4
sin
cos cos
sin
15
15
15
15
Решение:
Заданное выражение можно «свернуть» в синус суммы
аргументов:
4
4
sin
cos cos
sin
15
15
15
15
4
3
sin
sin
3
2
15 15
11.
Пример 4 Вычислить:sin 440 cos140 sin 460 cos 760
Решение:
По формулам приведения найдём:
sin 46 sin 90 44 cos 44
0
0
0
0
cos 76 cos 90 14 sin 14
0
0
0
0
Подставим в исходное выражение:
sin 44 cos14 sin 46 cos 76
0
0
0
0
sin 44 cos 14 cos 44 sin 14
1
0
0
0
sin 44 14 sin 30
2
0
0
0
0
12.
Пример 5 Упростить выражение:3 cos x sin x
Решение:
В заданном выражении вынесем множитель 2 за
скобки:
3
1
2
cos x sin x
2
2
Вспомним, что
3
1
cos ;
sin
2
6 2
6
13.
31
cos x sin x
3 cos x sin x 2
2
2
2 cos cos x sin sin x
6
6
2 cos x
6
14.
Повторим еще раз формулы:sin x y sin x cos y cos x sin y
sin x y sin x cos y cos x sin y
cos x y cos x cos y sin x sin y
cos x y cos x cos y sin x sin y












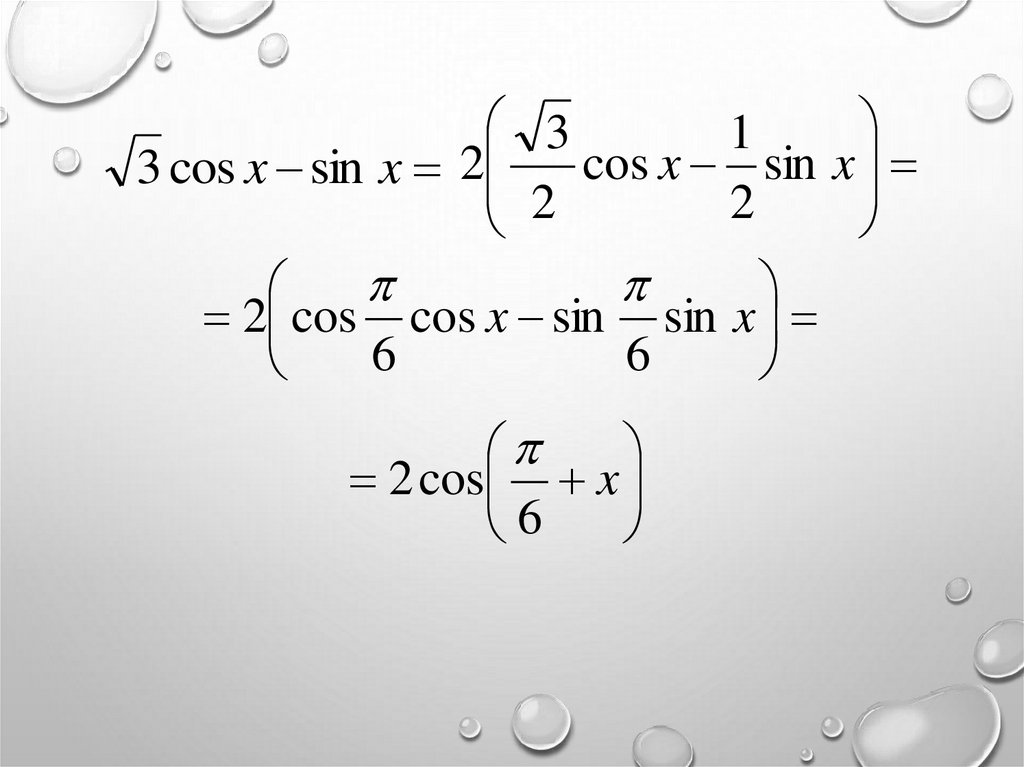

 Математика
Математика








