Похожие презентации:
Дифференциальные уравнения. Основные понятия
1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
2. §1. Основные понятия.
Прирешении
различных
задач
математики, физики, химии и других
наук
часто
пользуются
математическими моделями в виде
уравнений, связывающих независимую
переменную, искомую функцию и её
производные.
Такие
уравнения
называются
дифференциальными.
(Термин принадлежит
Г. Лейбницу,
1676г.)
3.
• Дифференциальнымуравнением
(ДУ)
называется
уравнение,
содержащее
независимую
переменную,
искомую
функцию и её
производные
или
дифференциалы.
или
dy d 2 y
dny
F x, y, , 2 ,..., n 0
dx dx
dx
F x, y, y , y ,..., y n 0
4. Примеры ДУ:
26y x y 0
y 2 xy 0
y 4 x
y
y xe
x dy 2 y dx
x dy y ln x dx
5.
• Наивысшийвходящей
в
порядком ДУ.
порядок
производной,
уравнение,
называется
• Решением ДУ называется функция, которая
при подстановке в уравнение обращает его
в тождество.
• Если искомая функция зависит от одной
переменной,
то
ДУ
называют
обыкновенным, если от нескольких – ДУ в
частных производных.
6. Пример 1. Показать, что данная функция является решением ДУ
Процесс нахождения решений дифференциальногоуравнения
называется
интегрированием
дифференциального уравнения.
Пример 1. Показать, что данная функция
y C1 sin x C2 cos x, C1 , C2 R
является решением ДУ
y y 0
7. Решение:
y C1 cos x C2 sin xy C1 sin x C2 cos x
Подставим:
C1 sin x C2 cos x C1 sin x C2 cos x 0
0 0
y C1 sin x C2 cos x являются
Т.о. функции вида
решениями данного ДУ при любом выборе постоянных С1
и С2:
C1 1 u C2 0 : y sin x
C1 0 u C2 2 : y 2 cos x
C1 3 u C2 1 : y 3sin x cos x
8. Задачи, приводящие к дифференциальным уравнениям
• Материальная точка массы m замедляет своедвижение под действием силы сопротивления
среды, пропорциональной квадрату скорости
V. Данный процесс описывается
дифференциальным уравнением
k 2
V V
m
k 0 - коэффициент пропорциональности,
(знак минус указывает на то, что скорость тела
уменьшается).
9.
• Закон изменения массы радия взависимости от времени (радиоактивный
распад) описывается ДУ
dm
где
k m
dt
k 0 -коэффициент пропорциональности,
-масса радия в момент времени t.
m(t )
10.
• «закон охлаждения тел», т.е. законизменения температуры тела в зависимости
от времени, описывается уравнением
dT
k (T t0 ), где
dt
T (t ) - температура тела в момент времени t ,
k - коэффициент пропорциональности,
t 0 -температура воздуха (среды охлаждения)
11.
• Зависимость массы x вещества,вступившего в химическую реакцию, от
времени t во многих случаях описывается
уравнением,
dx
k x
dt
где k - коэффициент пропорциональности
• «Закон размножения бактерий», т.е.
зависимость массы m бактерий от времени
t описывается уравнением mt k m .
12.
• Закон изменения давления воздуха взависимости от высоты над уровнем моря
описывается уравнением,
dp
k p
dh
где p ( h ) -атмосферное давление воздуха
на высоте h .
Приведенные примеры указывают на
исключительно важную роль ДУ при решении
самых разнообразных задач.
13. Дифференциальные уравнения I порядка
14.
• ДУ I порядка имеет видF x, y, y 0
или
dy f ( x, y ) dx
y f ( x, y )
Уравнение
связывает
независимую
переменную x , искомую функцию y и её
производную y .
• Общим решением ДУ I порядка называется
функция y ( x, C ) ,
содержащая
одну
произвольную
постоянную
С.
Уравнение
Φ(x,y,С) = 0 , задающее в неявном виде решение
дифференциального
уравнения,
называется
общим интегралом ДУ.
15.
• Частным решением ДУ I порядканазывается любая функция y ( x,C 0 )
полученная из общего решения y ( x, C )
при конкретном значении постоянной С=С0.
или
( x, y, C0 ) 0 (частный интеграл)
16. Пример 2. ДУ:
2ДУ: y 3x
Пример 2.
y x C -общее решение
C 2 : y x3 2
C 1 : y x 3 1
C 0: y x
3
частные решения
3
y x C 3x 2
3
3
3
y x 2 3x 2
y x 1 3x 2
3x
y x
3
2
17. Геометрически:
• Общее решение ДУ y ( x, C ) есть семействоинтегральных кривых на плоскости Оху;
• Частное решение ДУ y ( x,C 0 ) -одна кривая
этого семейства, проходящая через точку ( x0 , y 0 )
y 3x 2
у
y x 3 C -общее решение
y x 1 -частное решение
3
(х0, у0)
х
18.
• Условие, что при х=х0 функция у должнабыть равна заданному числу у0 называется
начальным условием.
y ( x0 ) y 0
или
y x x0 y 0
• Задача отыскания конкретного частного
решения данного ДУ по начальным данным
называется задачей Коши (Cauchy).
19. Пример 3. Решить задачу Коши:
Решение:y e
3 x
,
2
y (0)
3
1 3 x
y e C -общее решение
3
2
Подставим в общее решение начальные условия: y (0)
3
2
1 3 0
e C
3
3
у 2
0;
3
х
2
1
C
3
3
2 1
C 1
3 3
1 3 x
y e 1 -частное решение
3
20. Теорема существования и единственности решения задачи Коши.
• Если в уравнении y f ( x, y )функция f(x,y) и
её частная производная f y ( x; y ) непрерывны в
некоторой области D, содержащей точку (х0;у0), то
существует единственное решение y (x)
этого уравнения, удовлетворяющее начальному
условию y ( x0 ) y0
21. ДУ I порядка с разделёнными переменными.
• Если каждая часть ДУ представляет собойпроизведение некоторого выражения, зависящего
от одной переменной, на дифференциал этой
переменной, то говорят, что переменные в этом
уравнении разделены.
M ( x) dx N ( y ) dy 0
В
этом
случае
проинтегрировать:
уравнение
достаточно
M ( x) dx N ( y) dy C
22. Пример 4. Решить ДУ:
Пример 4.x dx y dy 0
Решить ДУ:
Решение:
общее решение:
y 2 x2 C
или
y x C
y dy x dx
у
y dy x dx
y2
x2
C
2
2
y 2 x 2 2C
С
2
2
С
2
0
х
Геометрически:
получили
семейство
концентрических окружностей с центром в
начале координат и радиусом С.
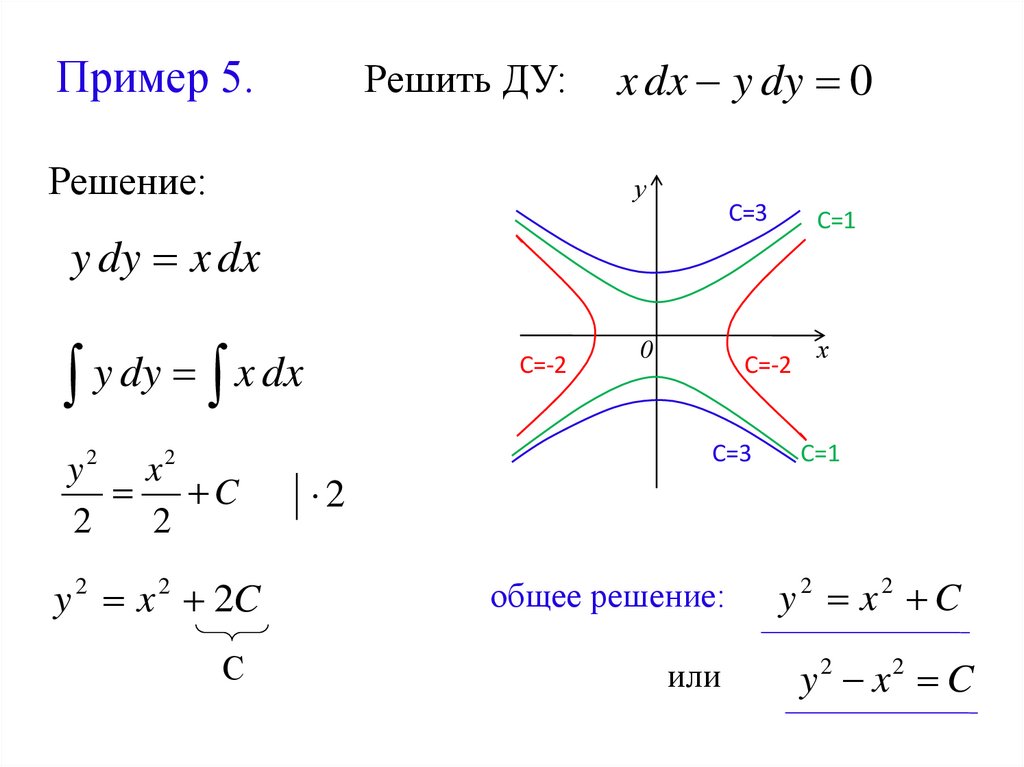
23. Пример 5. Решить ДУ:
Решение:x dx y dy 0
у
С=3
y dy x dx
y dy x dx
y2 x2
C
2
2
С=-2
2
0
С=1
С=-2
С=3
х
С=1
y 2 x 2 2C
общее решение:
y2 x2 C
С
или
y 2 x2 C
24. ДУ I порядка с разделяющимися переменными.
• Уравнения, в которых переменные разделяются,называются ДУ с разделяющимися переменными.
M1 ( x) N1 ( y) dx M 2 ( x) N 2 ( y) dy 0
где
M1 ( x), M 2 ( x), N1 ( y), N 2 ( y)
некоторые функции.
25.
M1 ( x) N1 ( y) dx M 2 ( x) N 2 ( y) dy 0: N1 ( y) M 2 ( x) 0
M 1 x N1 y
M 2 x N 2 y
dx
dy 0
N1 y M 2 x
N1 y M 2 x
M 1 ( x)
N 2 ( y)
dx
dy 0
M 2 ( x)
N1 ( y )
интегрируем:
M 1 ( x)
N 2 ( y)
dx
dy C
M 2 ( x)
N1 ( y )
26. Замечание:
1. При проведении почленного деления ДУ наN1 ( y) M 2 ( x)
могут быть потеряны некоторые решения.
Поэтому следует отдельно решить уравнение
N1 ( y) M 2 ( x) 0
и установить те решения ДУ, которые не могут
быть получены из общего решения- особые
решения.
27.
2. Уравнение y f1 ( x) f 2 ( y) также сводитсяк уравнению с разделенными переменными.
dy
Для этого достаточно положить y
dx
и разделить переменные .
28. Пример 6. Найти общее и частное решение ДУ:
x dy y dx,Решение:
x dy y dx
dy dx
y
x
dy
dx
y x
y (5) 10
1) Найдём общее решение ДУ:
1
xy
ln y ln x C
ln y ln x ln C
ln y ln xC
y Cx
y Cx
⇒
y Cx
29.
Итак, общее решение ДУ:y Cx
2) Найдём частное решение ДУ, если y (5) 10
Подставим эти начальные условия в общее
решение ДУ и найдем С:
10 5 C
C 2
⇒
y 2 x - частное решение ДУ.
Ответ: общее решение y Cx
частное решение y 2 x
30.
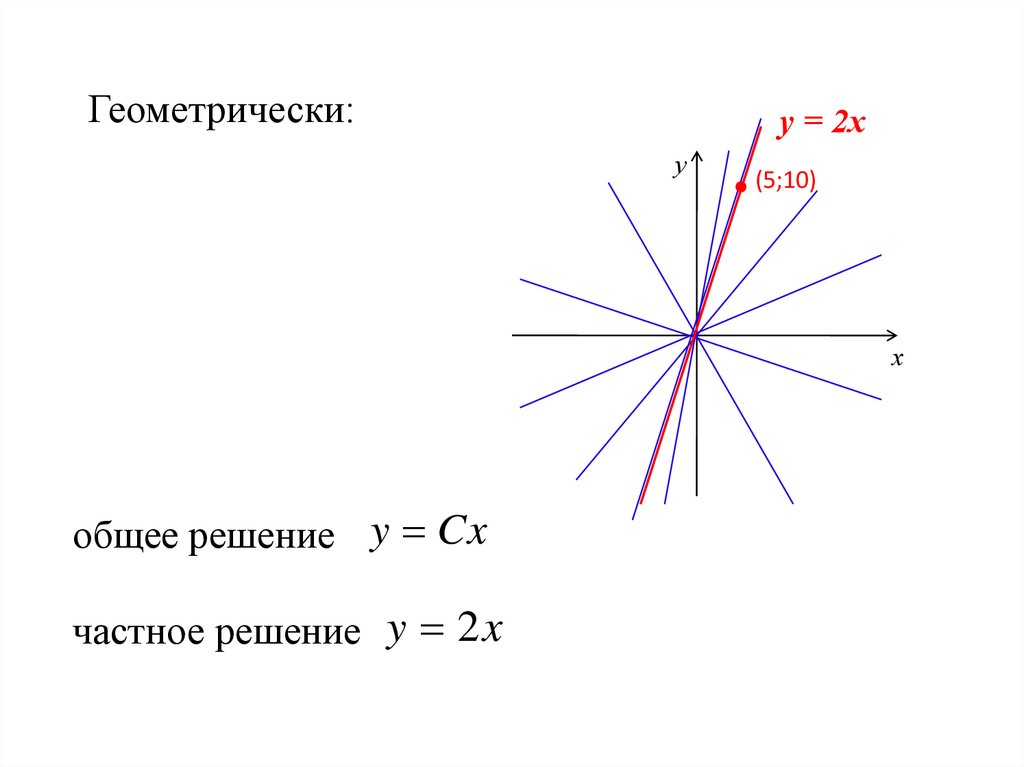
Геометрически:у = 2х
у
(5;10)
х
общее решение y Cx
частное решение y 2 x
31. Пример 7. Найти общее решение ДУ:
1 x y dx 1 y x dy 0Решение:
1 x y dx 1 y x dy 0
1 y x dy 1 x y dx
1 y
1 x
dy
dx
y
x
1
xy
32.
11
1 dy 1 dx
x
y
⇒
1
1
y 1 dy x 1 dx
ln y y ln x x C
ln y ln x y x C
ln xy y x C
или
ln xy y x C
Ответ. Общий интеграл: ln xy y x C
33.
Нахождение особого решения:Здесь уравнение N1 ( y) M 2 ( x) 0 имеет вид ху=0
Его решения х=0, у=0 являются решениями
данного ДУ, но не получаются из общего решения
ни
при
каких
значениях
произвольной
постоянной.
Значит, решения х = 0, у = 0 являются особыми.
34. Пример 8. Найти общее решение ДУ:
2 x sin y dx x 3 cos y dy 02
Решение:
2 x sin y dx x 3 cos y dy 0
2
x 3 cos y dy 2x sin y dx
2
cos y
2x
dy 2
dx
sin y
x 3
1
2
x 3 sin y
35.
cos y2x
sin y dy x 2 3 dx
ln sin y ln x 2 3 C
ln sin y ln x 2 3 ln C
C
ln sin y ln 2
x 3
⇒
sin y
C
sin y 2
x 3
C
sin y 2
x 3
C
x2 3
или
C
y arcsin 2
x 3
36.
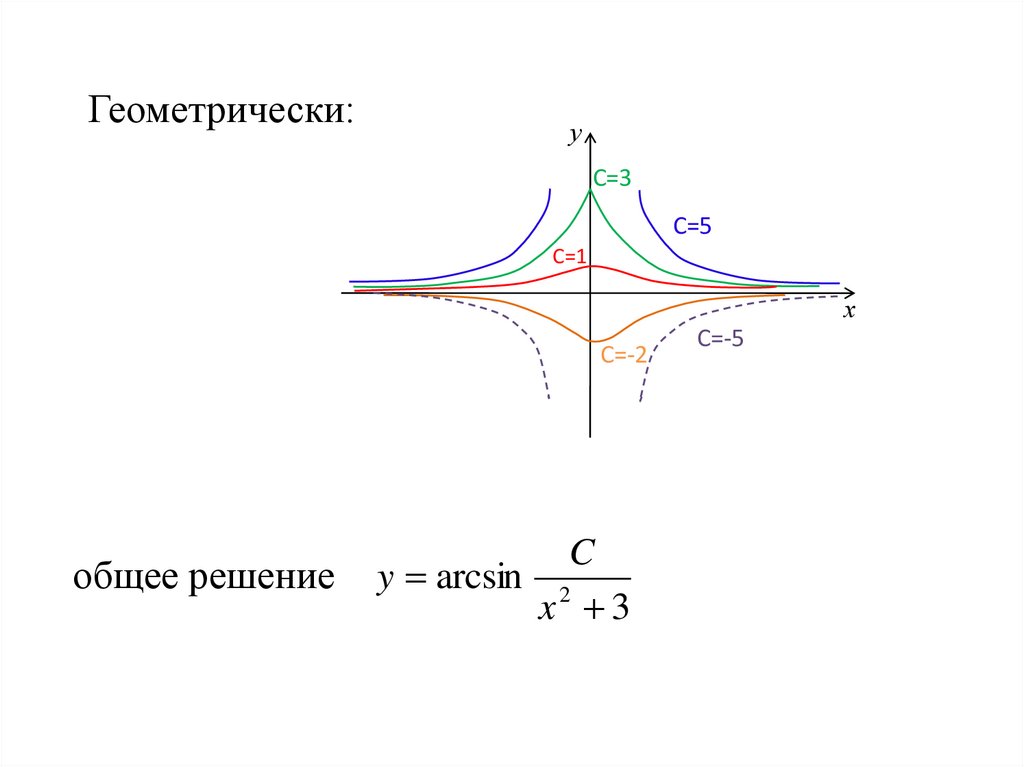
Геометрически:у
С=3
С=5
С=1
х
С=-2
общее решение
C
y arcsin 2
x 3
С=-5
37. Пример 9. Решить задачу Коши:
1 e2x
x
y y e ,
2
y(0) 1
Решение:
1) Найдём общее решение ДУ:
1 e
1 e y dy e dx
2x
2
x
x
e
y 2 dy
dx
2x
1 e
2x
dy
y
ex
dx
2
1
1 e2 x
38.
xe
2
y
dy 1 e 2 x dx
y3
arctan e x C
3
y3 3arctan e x 3C
или
3
y 3 3arctan e x C
С
Итак, общее решение ДУ: y3 3arctan e x C
39.
2) Найдём частное решение ДУ, еслиy ( 0) 1
Подставим эти начальные условия в общее
решение y 3 arctan e x C и найдем С:
1 3 arctan e C
1 3 arctan 1 C
0
1 3
4
y 3 3 arctan e x 1
3
y 3 arctan e 1
4
3
C
частное решение ДУ:
3
4
x
или
3
y 3 arctan e 1
4
3
x
40.
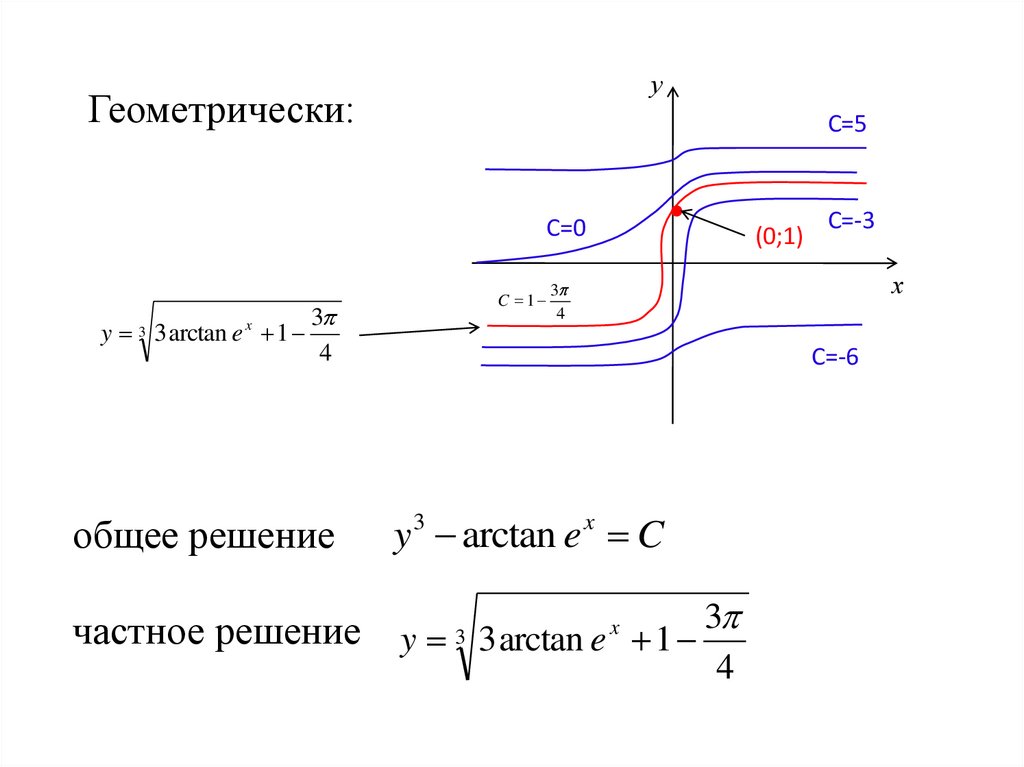
уГеометрически:
С=5
С=0
y 3 3 arctan e x 1
C 1
3
4
общее решение
(0;1)
С=-3
х
3
4
С=-6
y arctan e C
3
x
частное решение y 3 3 arctan e x 1 3
4
41. Пример 10. Решить задачу Коши:
Пример 10.Решение:
Решить задачу Коши:
dy
2( y 3),
dx
y (0) 4
1) Найдём общее решение ДУ:
dy 2( y 3) dx
dy
2 dx
y 3
1
y 3
42.
dyy 3 2 dx
ln y 3 2 x C
ln y 3 ln e2 x ln C
ln y 3 ln C e
y 3 C e
2x
y 3 C e
2x
2x
y 3 C e
⇒
Итак, общее решение ДУ:
2x
y 3 C e2 x
43.
2) Найдём частное решение ДУ, еслиy (0) 4
Подставим эти начальные условия в общее
2x
решение
и найдем С:
y 3 C e
4 3 C e0
4 3 C
C 1
Тогда, частное решение ДУ:
y 3 e2 x
44.
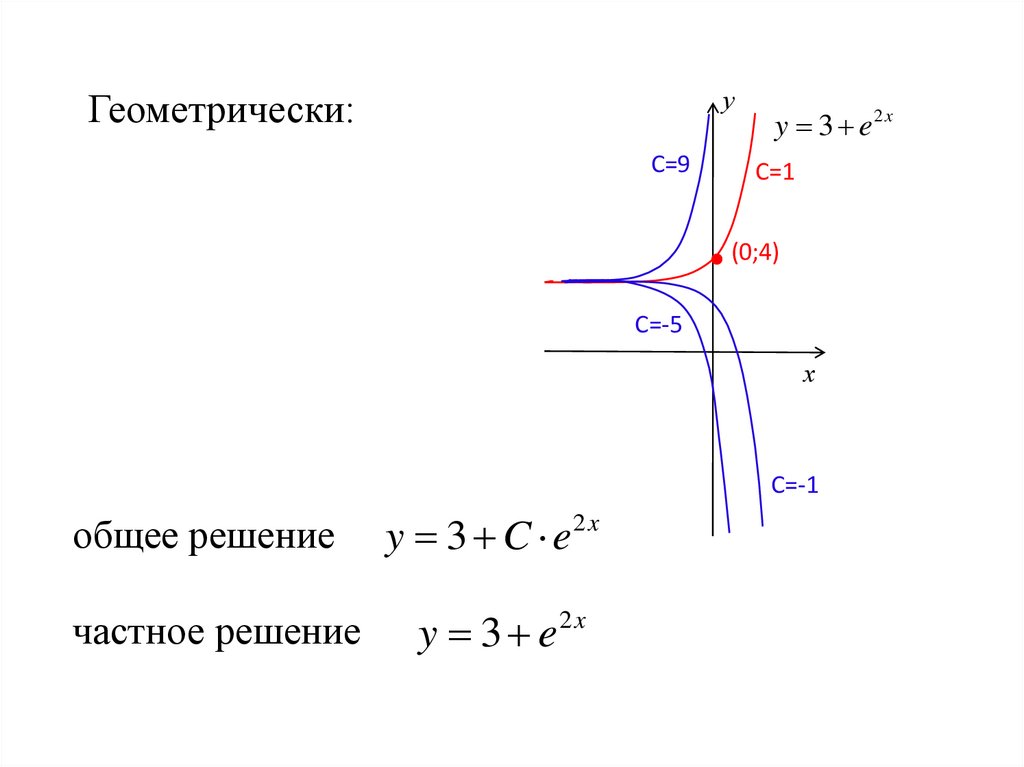
уГеометрически:
С=9
y 3 e2 x
С=1
(0;4)
С=-5
х
С=-1
общее решение
y 3 C e2 x
частное решение
y 3 e2 x
45. Однородные ДУ I порядка.
46.
Функция f(x;y) называется однородной
степени n, если умножение всех её
аргументов на одно и то же число t
равносильно умножению функции на tn, т.е.
f (tx; ty) t f ( x; y)
n
47. Пример 1.
f ( x; y) x 3 2 x 2 y 5 y 31)
- однородная функция
3-ей степени
f (tx; ty) tx 2 tx ty 5 ty
3
Так как
2
3
t x 2 t x t y 5 t y t x 2 x y 5 y
3
3
2
2
3
3
3
3
2
3
t f ( x; y )
3
48.
2)f ( x; y ) 3x 2 y
Так как
3)
f (tx; ty) 3tx 2ty t 3x 2 y t f ( x; y)
x y
f ( x; y )
2x 3y
Так как
- однородная функция 1-ой степени
- однородная функция 0-ой степени
tx ty
t x y
x y
f (tx; ty)
2tx 3ty t 2 x 3 y 2 x 3 y
f ( x; y) t 0 f ( x; y)
49.
4)y
f ( x; y ) x sin
x
2
Так как
5)
ty 2 2
y
f (tx; ty) tx sin t x sin t 2 f ( x; y )
tx
x
2
1
f ( x; y )
x y
Так как
- однородная функция 2-ой степени
- однородная функция (-1)-ой степени
1
1 1
1
1
f (tx; ty)
t
tx ty t x y
x y
t 1 f ( x; y )
50.
ДУ I порядка y f ( x; y ) называется
однородным, если f(x;y)- однородная
функция 0-ой степени, т.е.
f (tx; ty) f ( x; y )
51.
Однородное ДУ I порядка y f ( x; y )можно записать в виде:
y
y
x
Т.к.
f ( x; y ) f (tx; ty) , то если положить t 1
x
Получаем:
x y
y
y
f ( x; y ) f ; f 1;
x x
x
x
52.
yРешение однородного ДУ I порядка y
x
Это уравнение преобразуется в уравнение с
разделяющимися переменными при помощи
замены переменной
y
z
x
или
y z x
y z x
y z x z x
y z x z
53.
yи y в уравнение y
x
Подставив y
получим
уравнение с разделяющимися переменными. Найдя
его общее решение (или общий интеграл) следует
заменить в нем z на
y
.
x
54. Пример 2. Найти общее решение ДУ:
yy
y tg
x
x
y
Это однородное ДУ вида y
x
y
z
x
⇒
y z x
55.
y z x zz x z z tg z
dz
x z z tg z
dx
dz
x tg z
dx
dz dx
tg z x
56.
dzdx
tg z x
ln sin z ln x C
ln sin z ln x ln C
ln sin z ln Cx
sin z Cx
sin z Cx
sin z Cx
z arcsin Cx
y
arcsin Cx
x
y x arcsin Cx
57. Пример 3. Решить задачу Коши: , если y(1)=0
Пример 3.Решить задачу Коши:
2x y
y
2x
, если y(1)=0
2x y 2x y
1 y
y
1
2x
2x 2x
2 x
y
Это однородное ДУ вида y
x
y
z
x
⇒
y z x
58.
1 yy 1
2 x
dz
z
x
1
dx
2
1
z x z 1 z
2
dz 2 z
x
dx
2
dz
z
x z 1
dx
2
dz
z
x
1 z
dx
2
dz
dx
2 z 2x
dz
dx
2 z 2x
59.
1ln 2 z ln x C
2
2
2 ln 2 u ln x C
ln 2 z ln x ln C
2
C
ln 2 z ln
x
C
2
2 z
x
C
2 z
x
2
C
2 z
x
C
z 2
x
y
C
2
x
x
60.
Cy x 2
x
- общее решение
C
0 1 2
1
0 2 C
C 2
Найдем С:
2
y x 2
x
или
y 2 x x
- частное решение
61.
Уравнение вида M ( x; y ) dx N ( x; y ) dy 0
называется
однородным, если M(x;y)
и N(x;y) - однородные функции
одной и той же степени.
62. Пример 4. Найти общее решение ДУ:
dydy
y x
xy
dx
dx
2
dy
dy
y x
xy
dx
dx
2
2
2
dx
y dx x dy xy dy
2
2
y dx x xy dy 0 - уравнение однородное вида
2
M(x;y)
2
N(x;y)
M ( x; y ) dx N ( x; y ) dy 0
63.
yu
x
⇒
y u x
y u x u x
dy
u x u x
dx
dy u x dx u x dx
du
du
xdx udu
dx
dy x du u dx
64.
u x dx x x ux x du u dx 0y 2 dx x 2 xy dy 0
2
2
2
u 2 x 2 dx x 3du x 3u du x 2u dx x 2u 2 dx 0
x 1 u du ux dx 0
3
2
x 1 u du ux dx
u 1
dx
du
u
x
u 1
dx
u du x
3
2
(*)
65.
dudx
du u x
u ln u ln x C
u ln u ln x ln C
ln eu ln u ln Cx
eu
ln
ln Cx
u
u
e
Cx
u
eu
Cx
u
eu uCx
y
x
y
e Cx
x
y
x
e Cy
- общий интеграл
66.
Это однородное ДУ можно привести к видуy
y
x
dy
dy
y x
xy
dx
dx
dy
2
2
y x xy
0
dx
2
2
x xy y y
2
2
2
y
2
2
2
y
y
y
x
y
x x y x y x
y 1
2 y
x 1
x x
67.
yu
x
⇒
y u x
2
y
x
y
y
1
x
⇒
u2
u x u
u 1
du
u2
x
u
dx u 1
du u 2 u 2 u
x
dx
u 1
68.
duu
x
dx u 1
u 1
dx
du
u
x
u 1
dx
u du x
- получили (*)
69. Пример 5. Найти общее решение ДУ:
x 2 y dx 2xy dy 02
x 2 y dx 2xy dy 0
2
2
N(x;y)
M(x;y)
y
z
x
⇒
y z x
y z x z x
dy
z x zx
dx
2
- уравнение однородное вида
M ( x; y ) dx N ( x; y ) dy 0
dy z x dx z x dx
dz
dy
x dx z dx
dx
dy x dz z dx
70.
22 2
x
2
z
x dx 2 x zx x dz z dx 0
2
2 2
3
2 2
x
2
x
z
dx
2
x
z
dz
2
x
z dx 0
x dx 2 x z dz 0
2
dx
2 z dz
x
dx
2 z du x
z 2 ln x C
C
z ln
x
2
3
2
C
y
ln
x
x
C
2
2
y x ln
x
y 2 x 2 ln Cx
y 2 x 2 ln Cx 0
71. Пример 6. Найти общее решение ДУ:
22
xy y x y
Это однородное ДУ можно привести к виду
2
2
xy y x y
xy y x 2 y 2
2
2
x
y
y
y
x
x
:x
y
y
x
72.
yx2 y2
y
x
x2
y
y
y 1
x
x
y
u
x
⇒
2
y u x
y u x u x
du
y x
u
dx
73.
dux
u u 1 u2
dx
du
x
1 u2
dx
du
dx
x
1 u2
du
dx
2
x
1 u
ln u 1 u 2 ln x C
u 1 u 2 Cx
y
y2
1 2 Cx
x
x
x2 y2
y
Cx
x
x
y x 2 y 2 Cx 2
общее решение
74.
y x 2 y 2 Cx 2- общее решение
или
x y Cx y
2
2
2
x y Cx y
2
2
2
2
2
x 2 y 2 Cx 4 2 yCx 2 y 2
x 2 x 2 Cx 2 2 yC
1 C ( x 2 2 y)
1
C
2
x 2y
- общее решение
75.
Линейные ДУ I порядка.76.
Линейным дифференциальным уравнением первогопорядка называется ДУ 1-го порядка, линейное
относительно неизвестной функции y и ее
производной y .
В общем случае линейное уравнение 1-го порядка
можно
записать в виде
y + p(x) y = f(x) ,
(1)
где p(x) , f(x) – заданные непрерывные функции.
77.
Если f(x) ≡ 0 , то линейное уравнениеназывается однородным.
В противном случае уравнение называется
неоднородным.
Линейное однородное уравнение
y +p(x) y = 0 (2)
является уравнением с разделяющимися
переменными.
p ( x) dx
Его общее решение: y C e
, C .
78.
Рассмотрим линейное неоднородное уравнение (1):y + p(x) y = f(x) .
Существуют два метода его интегрирования.
(1)
I) Метод вариации постоянной (метод Лагранжа)
1) Интегрируем однородное уравнение y + p(x) y = 0, соответствующее данному неоднородному уравнению.
Его общее решение имеет вид :
y C e
p ( x ) dx
.
2) Полагаем, что решение неоднородного уравнения по
структуре совпадает с решением соответствующего линейного однородного уравнения.
Оно имеет вид
p ( x) dx
y C ( x) e
.
Функцию C(x) найдем, подставив y и y в исходное неоднородное уравнение (1).
79.
Получим:C ( x)
p ( x ) dx
f ( x) e
dx C .
Таким образом, общее решение линейного неоднородного
уравнения (1) имеет вид:
p ( x) dx
p ( x ) dx
y ( x) f ( x) e
dx C e
.
Замечания.
1) Раскроем скобки в :
y ( x) C e
p ( x ) dx
e
p ( x ) dx
p ( x ) dx
f ( x) e
dx .
Заметим, что первое слагаемое – общее решение линейного
однородного уравнения, а второе – частное решение
линейного неоднородного уравнения (получается из общего
решения при C = 0).
80.
2) Так как ex 0, то любую функцию y(x) можно записать в видеy ( x) x
y ( x) x e .
e
Это является основанием метода вариации постоянной.
(12)
81.
II) Метод Бернулли.Будем искать решение уравнения (1)
следующем виде: y u ( x) v( x)
в
Тогда
y = u v + u v .
Подставим y и y в уравнение (1) и
получим:
u v + u v + p(х)uv = f(x)
илиu v + u [ v + pv ] = f(x) .
Полагаем, что функция v(x) такова, что
[ v + pv ] = 0 .
Тогда
u v = f(x) .
82.
Система позволяет однозначно определить v(x) и u(x) .При этом получим
v( x) e
u ( x)
p( x) dx
,
p ( x ) dx
f ( x) e
dx C .
p( x)dx
p( x)dx
y e
f ( x) e
dx C .
Замечание. Линейное неоднородное уравнение вида
y + p(x) y = b
проще интегрировать как уравнение с разделяющимися
переменными.
83.
y 2xy 2xПример.
y u v uv
Полагаем y u v , тогда
Подставим y и y в уравнение, получим
u v u v 2x u v 2x
Сгруппируем второе и третье слагаемое и
вынесем за скобки общий множитель u
u v u (v 2x v) 2x
Сначала решаем уравнение
v 2x v 0
84.
v 2x v 0dv 2 xv
dx
dv
2 xdx
v
dv
2 xdx
v
ln v x 2
2
x
v e
85.
Теперь решим уравнениеu v 2x
2
u e x 2 x
2
du
x
2x e
dx
2
du 2 x e x dx
2
x
du 2 x e dx
x
u e
2
C
86.
Итак, общее решение данного уравненияx
y u v (e
2
x
C) e
или
x
y 1 C e
2
2
87. Уравнения Бернулли
Уравнением Бернулли называется уравнение видаy + p(x) y = f(x) y n ,
(2)
где p(x) , f(x) – заданные непрерывные функции,
n 0 , n 1 (иначе это будет линейное уравнение).
Уравнение Бернулли можно привести к линейному уравнению.
Для этого надо
1) обе части уравнения разделить на y n ,
2) сделать замену z = y 1 – n .
Замечания.
1) Уравнение Бернулли при n > 0 имеет решение y = 0 . Оно
будет частным решением при n > 1 (обычно входит в общее
при C = ) и особым при 0 < n < 1 .
88.
2) Решив получившееся после замены линейное уравнениеметодом Бернулли, получим:
z = u(x) v(x) ,
1
y
y
n 1
n 1
u ( x) v( x) ,
1
1
,
u ( x) v( x)
1
n 1
1
y
u ( x)
1
n 1
1
v( x)
u~ ( x) v~( x) .
Таким образом, решение уравнения Бернулли можно сразу
искать в виде произведения двух функций методом Бернулли,
не приводя предварительно к линейному уравнению.























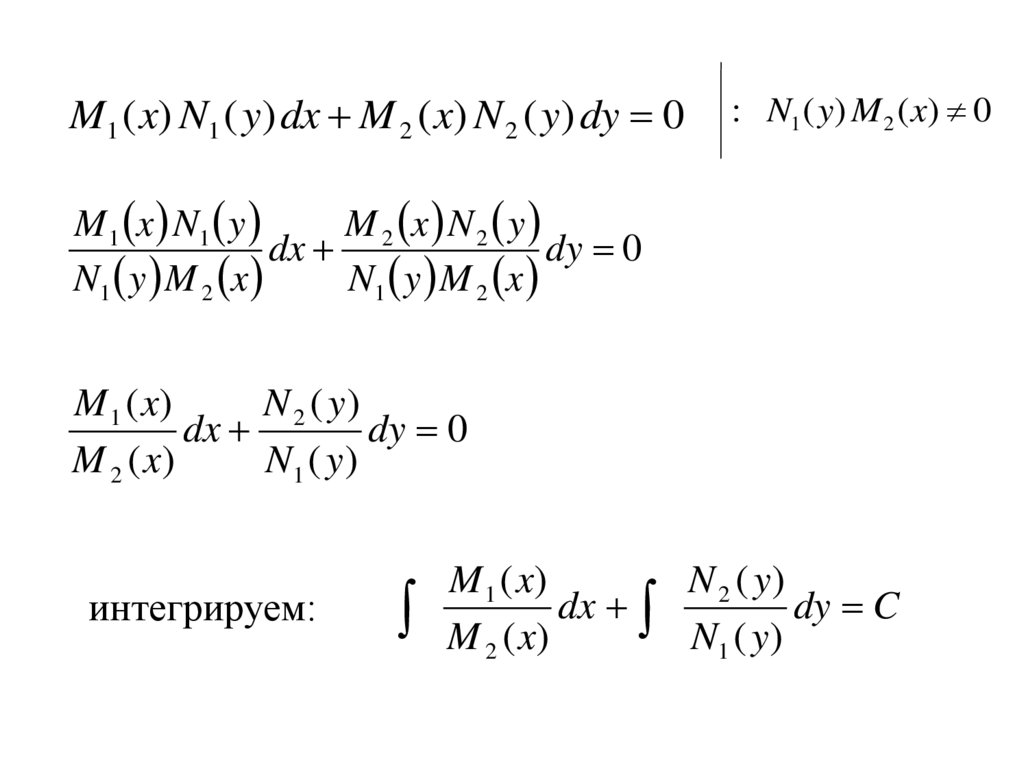


















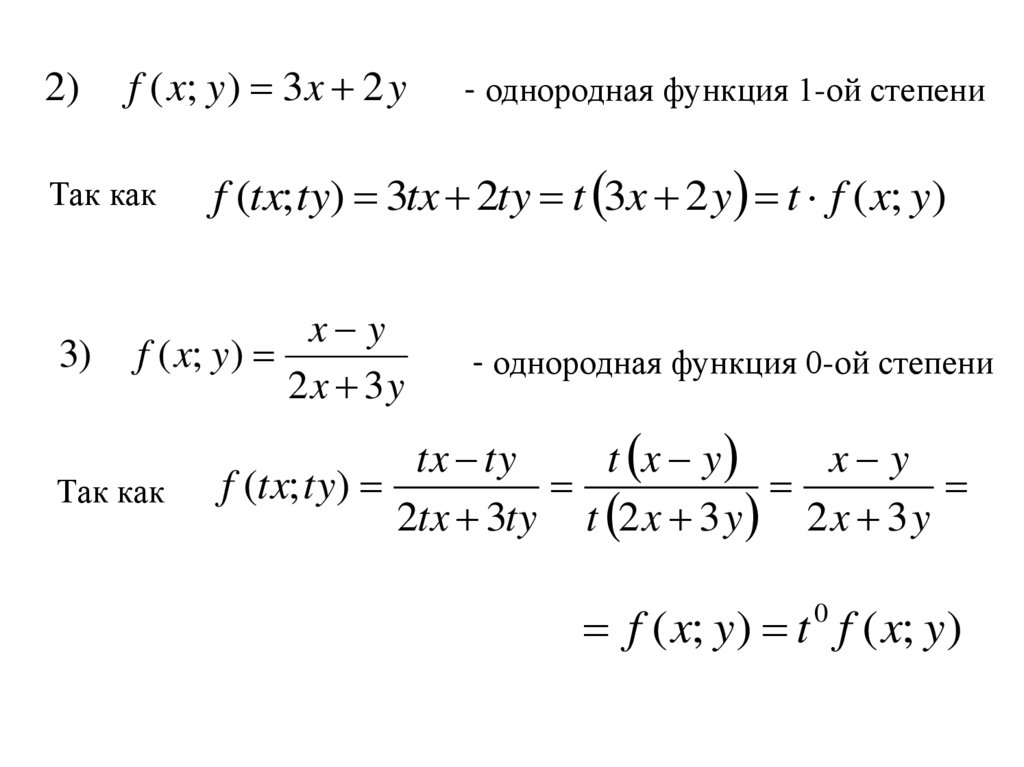






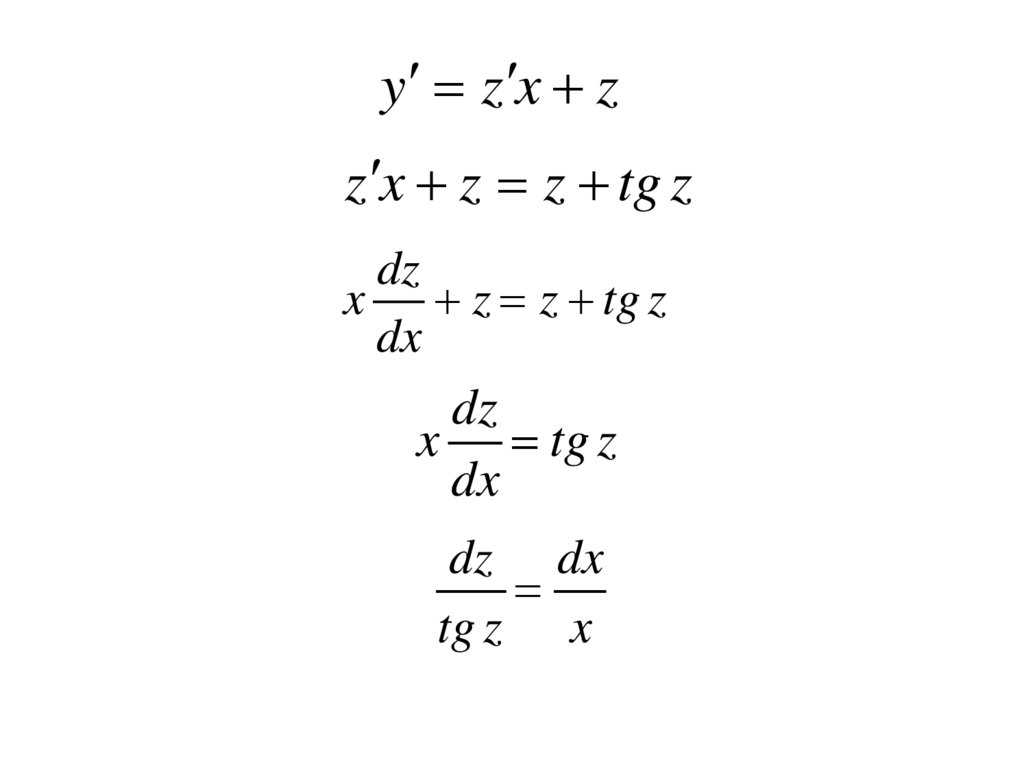


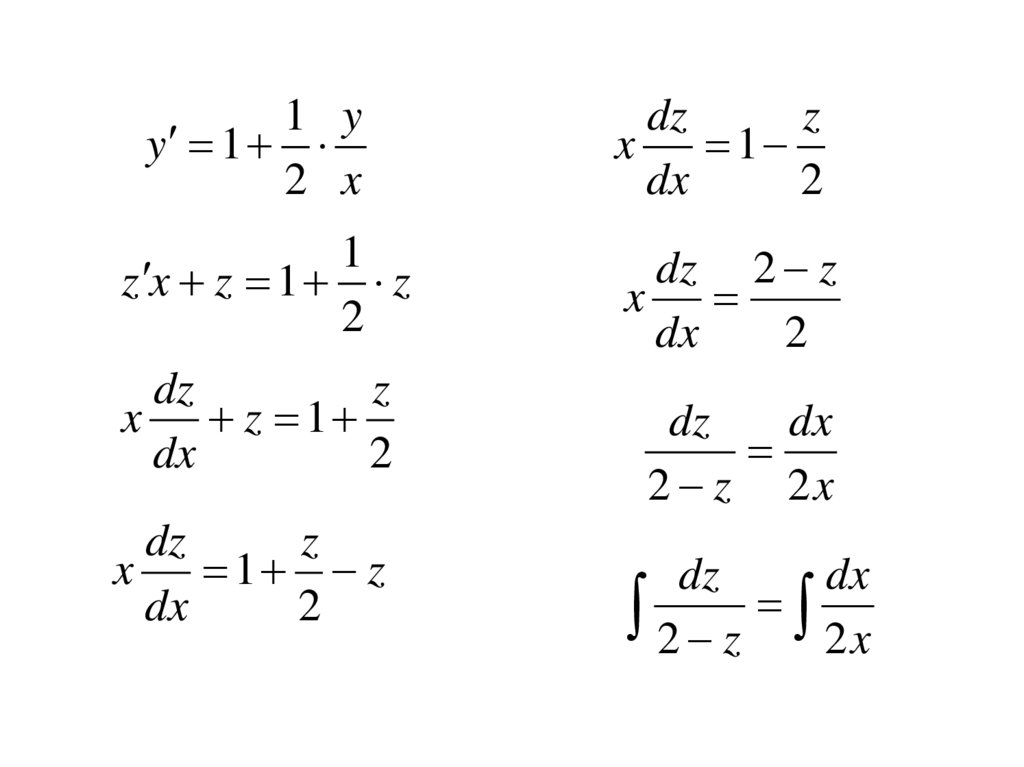
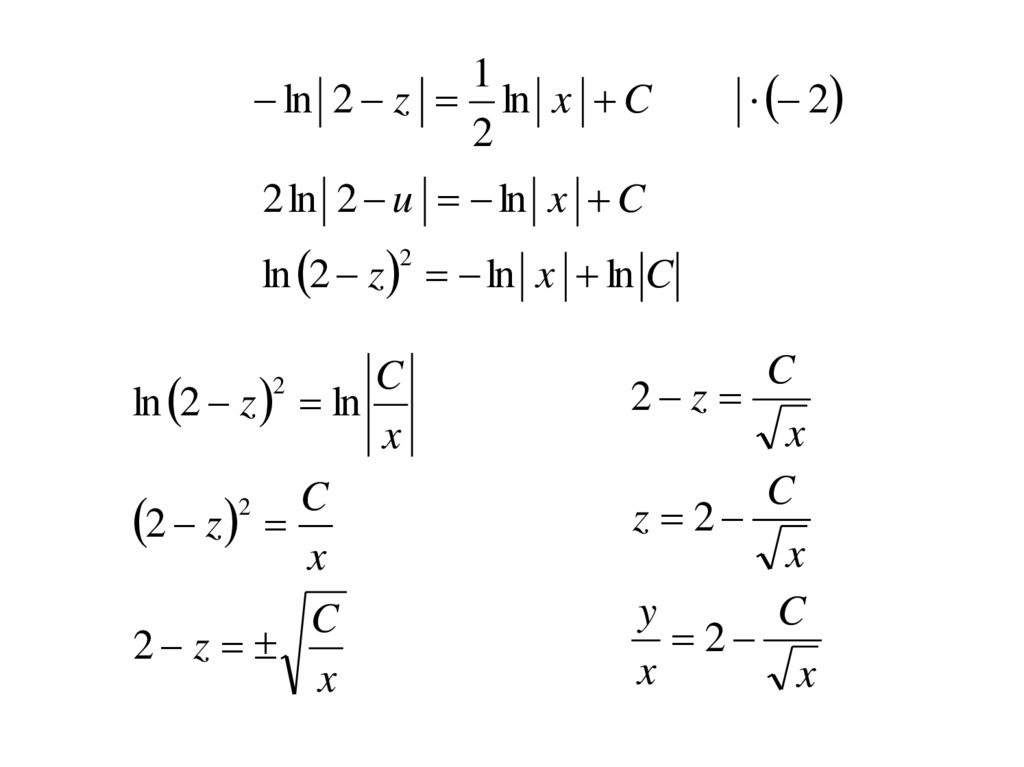
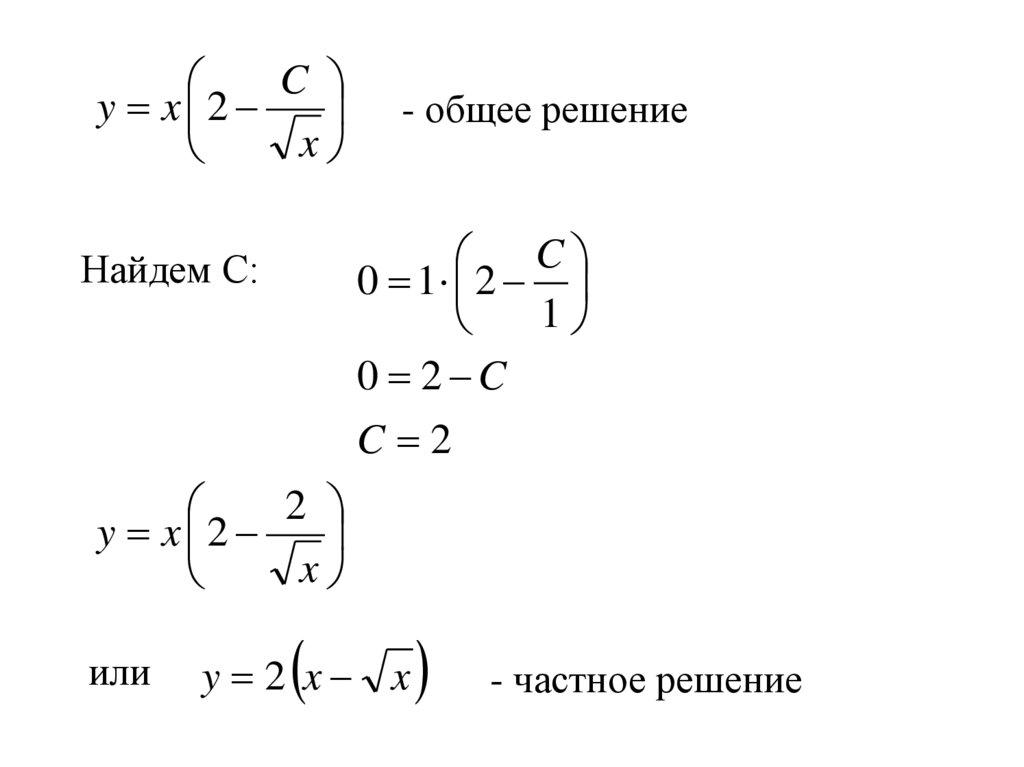


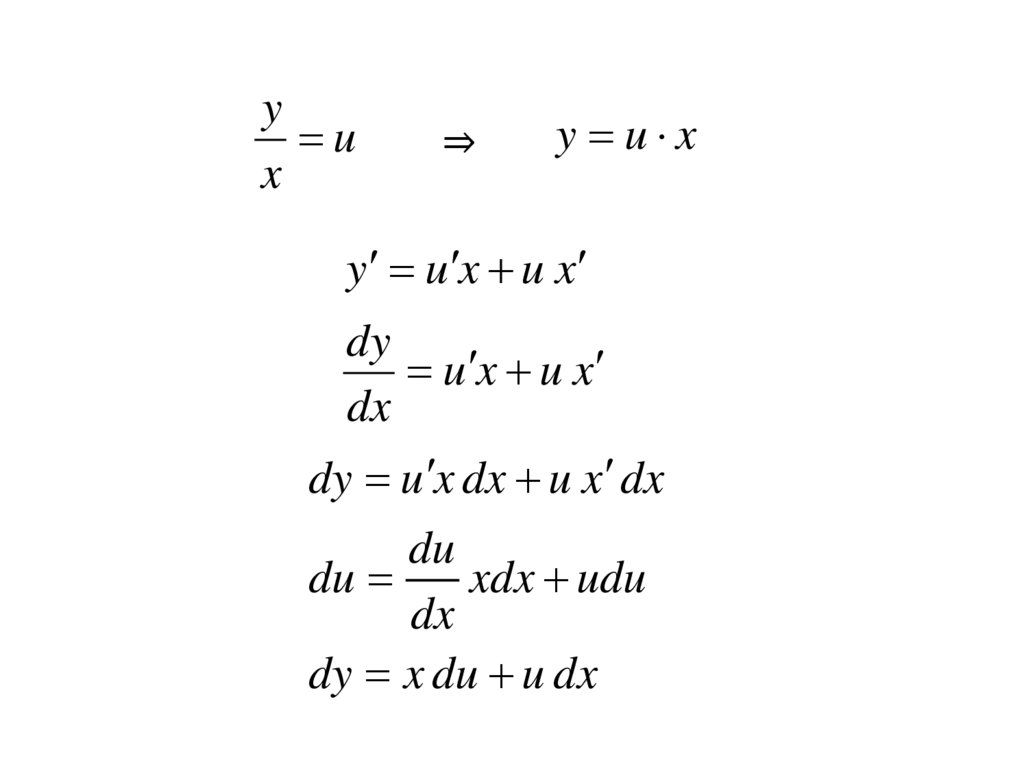
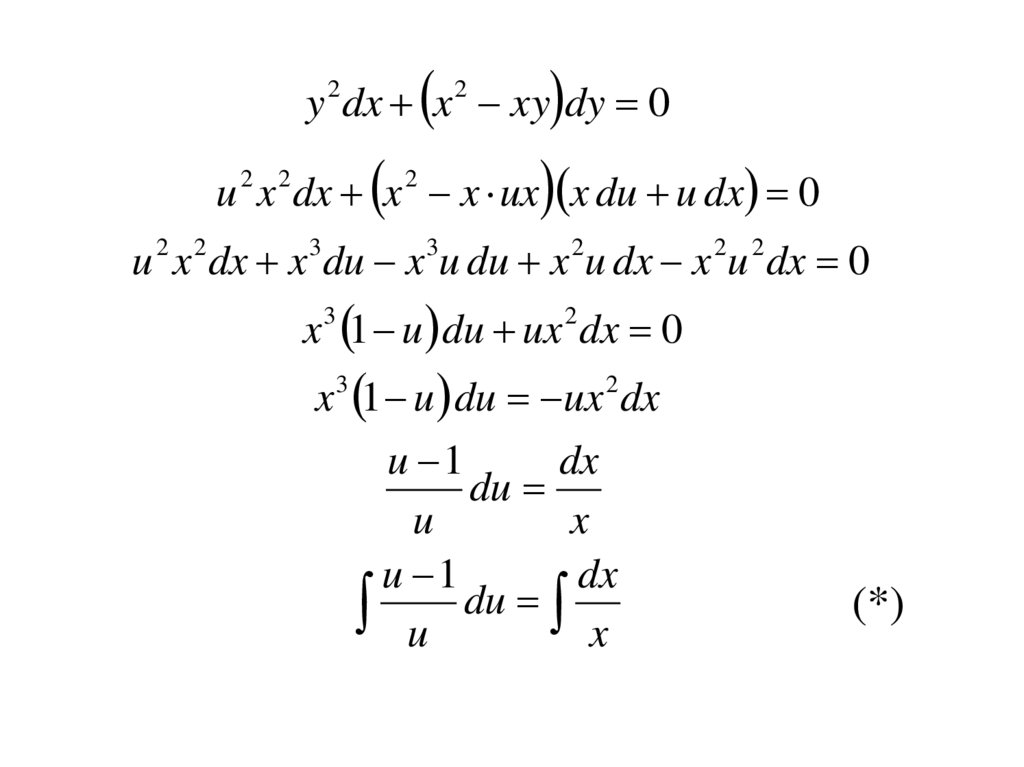


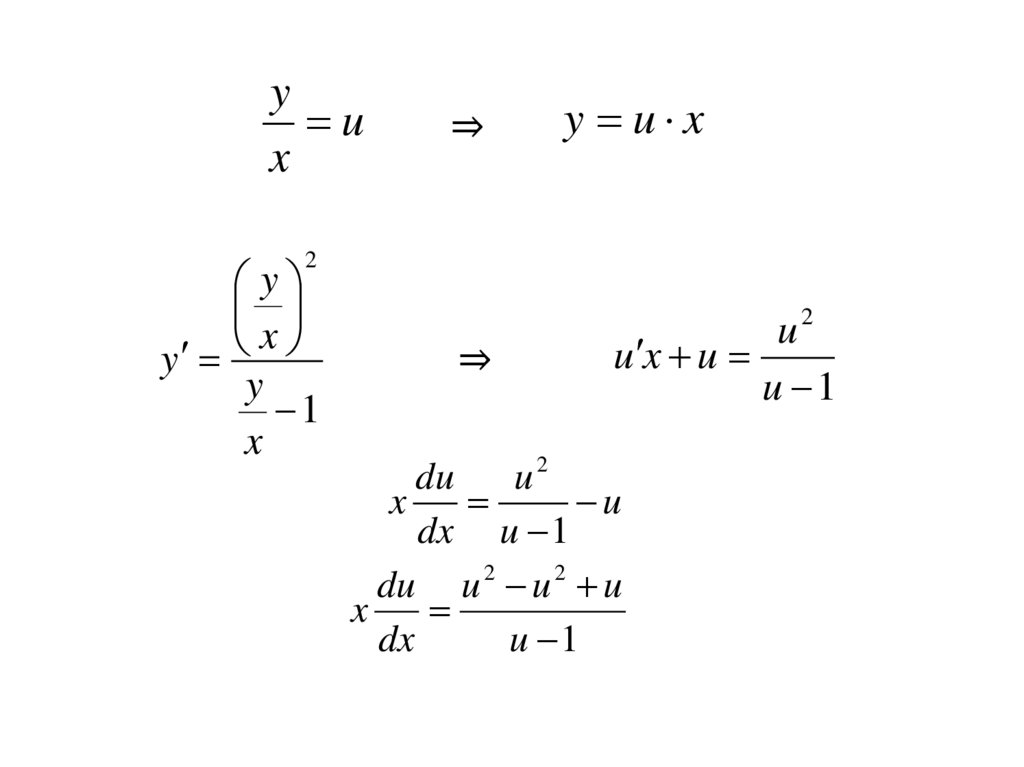















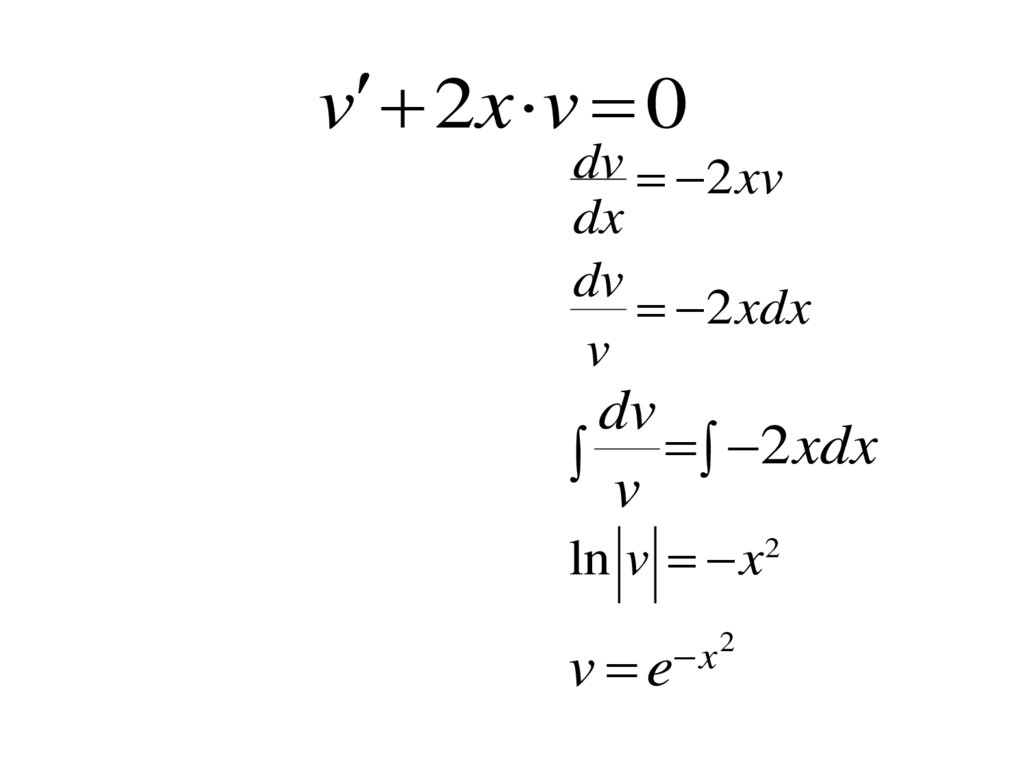
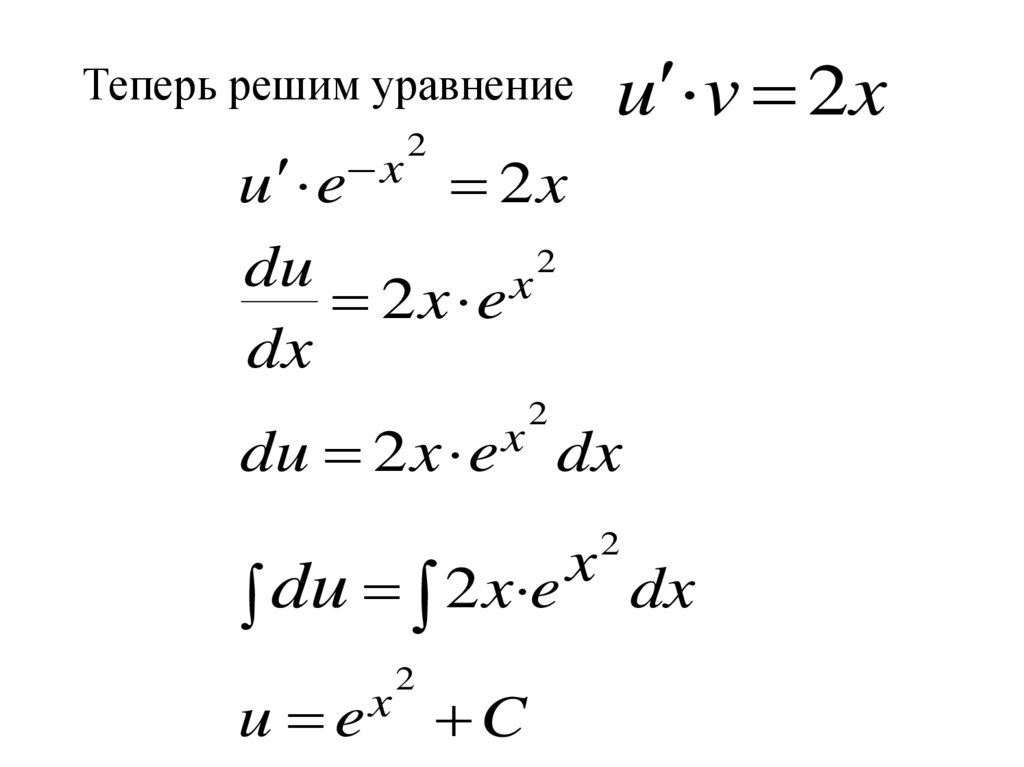



 Математика
Математика








