Похожие презентации:
Однородные дифференциальные уравнения I порядка
1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ-3
2. 4. Однородные ДУ I порядка.
3.
Функция f(x;y) называется однородной
степени n, если умножение всех её
аргументов на одно и то же число t
равносильно умножению функции на tn, т.е.
f (tx; ty) t f ( x; y)
n
4. Пример 1.
f ( x; y) x 3 2 x 2 y 5 y 31)
- однородная функция
3-ей степени
f (tx; ty) tx 2 tx ty 5 ty
3
Так как
2
3
t x 2 t x t y 5 t y t x 2x y 5 y
3
3
2
2
3
3
3
3
2
3
t f ( x; y )
3
5.
2)f ( x; y ) 3x 2 y
Так как
3)
f (tx; ty) 3tx 2ty t 3x 2 y t f ( x; y)
x y
f ( x; y )
2x 3 y
Так как
- однородная функция 1-ой степени
- однородная функция 0-ой степени
tx ty
t x y
x y
f (tx; ty)
2tx 3ty t 2 x 3 y 2 x 3 y
f ( x; y) t 0 f ( x; y)
6.
4)y
f ( x; y ) x sin
x
2
Так как
5)
ty 2 2
y 2
f (tx; ty) tx sin t x sin t f ( x; y )
tx
x
2
1
f ( x; y )
x y
Так как
- однородная функция 2-ой степени
- однородная функция (-1)-ой степени
1
1 1
1
1
f (tx; ty)
t
tx ty t x y
x y
t 1 f ( x; y )
7.
ДУ I порядка y f ( x; y ) называется
однородным, если f(x;y)- однородная
функция 0-ой степени, т.е.
f (tx; ty) f ( x; y )
8.
Однородное ДУ I порядка y f ( x; y )можно записать в виде:
y
y
x
Т.к.
f ( x; y ) f (tx; ty)
, то если положить
1
t
x
Получаем:
x y
y
y
f ( x; y ) f ; f 1;
x x
x
x
9.
yРешение однородного ДУ I порядка y
x
Это уравнение преобразуется в уравнение с
разделяющимися переменными при помощи
замены переменной
y
u
x
или
y u x
10.
yy
x
y
u
x
u x u
u x u x u
u x u (u )
du
x
(u ) u
dx
du
dx
(u ) u x
или
y u x
11.
dudx
(u) u x
F (u) ln x C
или
y
F ln x C -общее решение данного ДУ
x
12. Пример 2. Найти общее решение ДУ:
yy
y tan
x
x
y
Это однородное ДУ вида y
x
y
u
x
⇒
y u x
13.
yy
y tan
x
x
u x u x u tan u
du
x
u u tan u
dx
du
x
tan u
dx
du
dx
tan u x
14.
dudx
tan u x
ln sin u ln x C
ln sin x ln x ln C
ln sin x ln Cx
sin x Cx
sin x Cx
sin x Cx
u arcsin Cx
y
arcsin Cx
x
y x arcsin Cx
15. Пример 3. Решить задачу Коши: , если y(1)=0
Пример 3.Решить задачу Коши:
2x y
y
2x
, если y(1)=0
2x y 2x y
1 y
y
1
2x
2x 2x
2 x
y
Это однородное ДУ вида y
x
y
u
x
⇒
y u x
16.
1 yy 1
2 x
du
u
x
1
dx
2
1
u x u 1 u
2
du 2 u
x
dx
2
du
u
x
u 1
dx
2
du
u
x
1 u
dx
2
du
dx
2 u 2x
du
dx
2 u 2x
17.
1ln 2 u ln x C
2
2
2 ln 2 u ln x C
ln 2 u ln x ln C
2
C
ln 2 u ln
x
C
2
2 u
x
C
2 u
x
2
C
2 u
x
C
u 2
x
y
C
2
x
x
18.
Cy x 2
x
- общее решение
C
0 1 2
1
0 2 C
Найдем С:
C 2
2
y x 2
x
или
y 2 x x
- частное решение
19.
Уравнение вида M ( x; y ) dx N ( x; y ) dy 0
называется
однородным, если M(x;y)
и N(x;y)- однородные
функции
одной и той же степени.
20. Пример 4. Найти общее решение ДУ:
dydy
y x
xy
dx
dx
2
dy
dy
y x
xy
dx
dx
2
2
2
dx
y dx x dy xy dy
2
2
y dx x xy dy 0
2
M(x;y)
2
N(x;y)
- уравнение однородное вида
M ( x; y ) dx N ( x; y ) dy 0
21.
yu
x
⇒
y u x
y u x u x
dy
u x u x
dx
dy u x dx u x dx
dy x du u dx
22.
u x dx x x ux x du u dx 0y 2 dx x 2 xy dy 0
2
2
2
u x dx x du x u du x u dx x u dx 0
2
2
3
3
2
2
2
x 1 u du ux dx 0
3
2
x 1 u du ux dx
u 1
dx
du
u
x
u 1
dx
u du x
3
2
(*)
23.
dudx
du u x
u ln u ln x C
u ln u ln x ln C
ln eu ln u ln Cx
eu
ln
ln Cx
u
u
e
Cx
u
eu
Cx
u
eu uCx
y
x
y
e Cx
x
y
x
e Cy
- общее решение
24.
Это однородное ДУ можно привести к видуy
y
x
dy
dy
y x
xy
dx
dx
dy
2
2
y x xy
0
dx
x 2 xy y y 2
2
2
2
y
2
2
2
y
y
y
x
y
x x y x y x
y 1
2 y
x 1
x x
25.
yu
x
⇒
y u x
2
y
x
y
y
1
x
⇒
u2
u x u
u 1
du
u2
x
u
dx u 1
du u 2 u 2 u
x
dx
u 1
26.
duu
x
dx u 1
u 1
dx
du
u
x
u 1
dx
u du x
- получили (*)
27. Пример 5. Найти общее решение ДУ:
xx
2
2
2 y dx 2 xy dy 0
2
M(x;y)
y
u
x
N(x;y)
⇒
y u x
y u x u x
2 y 2 dx 2 xy dy 0
- уравнение однородное вида
M ( x; y ) dx N ( x; y ) dy 0
dy
u x u x
dx
dy u x dx u x dx
dy x du u dx
28.
xx
dx 2 x u du 2 x u dx 0
2
2u 2 x 2 dx 2 x ux x du u dx 0
2
2 x 2u 2
3
2
2
x 2 dx 2 x 3u du 0
dx
2u du
x
dx
2u du x
u 2 ln x C
C
u ln
x
2
2
C
y
ln
x
x
C
2
2
y x ln
x
y 2 x 2 ln Cx
y 2 x 2 ln Cx 0
29. Пример 6. Найти общее решение ДУ:
22
xy y x y
Это однородное ДУ можно привести к виду
2
2
xy y x y
2
2
xy y x y
y
y
x
x2 y2
x
:x
y
y
x
30.
yy
x y
x
x2
2
2
y
y
y 1
x
x
y
u
x
⇒
2
y u x
y u x u x
du
y x
u
dx
31.
dux
u u 1 u2
dx
du
x
1 u2
dx
du
dx
x
1 u2
du
dx
2
x
1 u
ln u 1 u 2 ln x C
u 1 u 2 Cx
y
y2
1 2 Cx
x
x
x2 y2
y
Cx
x
x
y x 2 y 2 Cx 2
общее решение
32.
y x 2 y 2 Cx 2- общее решение
или
x y Cx y
2
2
2
2
x y Cx y
2
2
2
2
x 2 y 2 Cx 4 2 yCx 2 y 2
x
2
x Cx
2
2
2 yC
1 C ( x 2 2 y)
1
C
2
x 2y
- общее решение









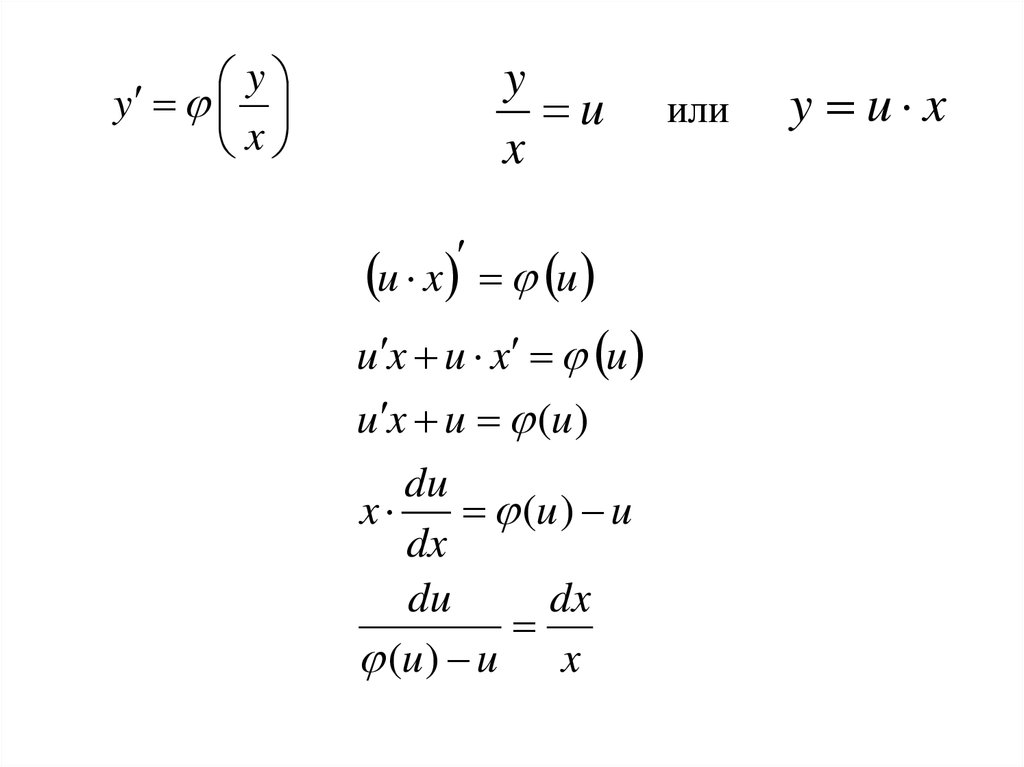






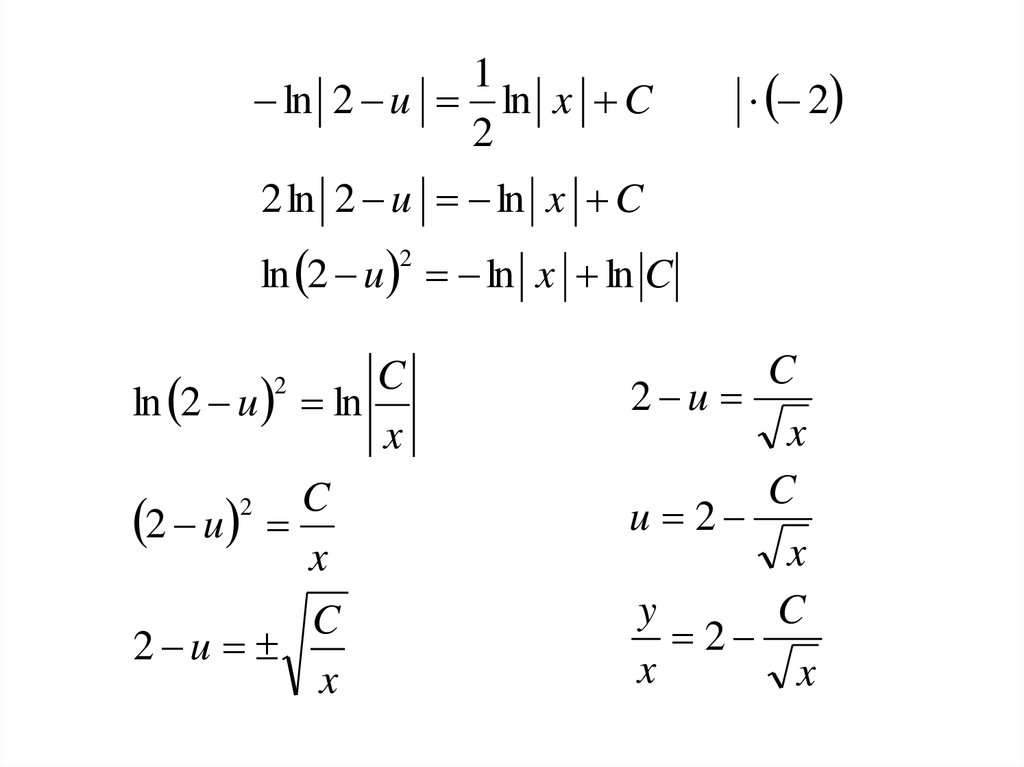
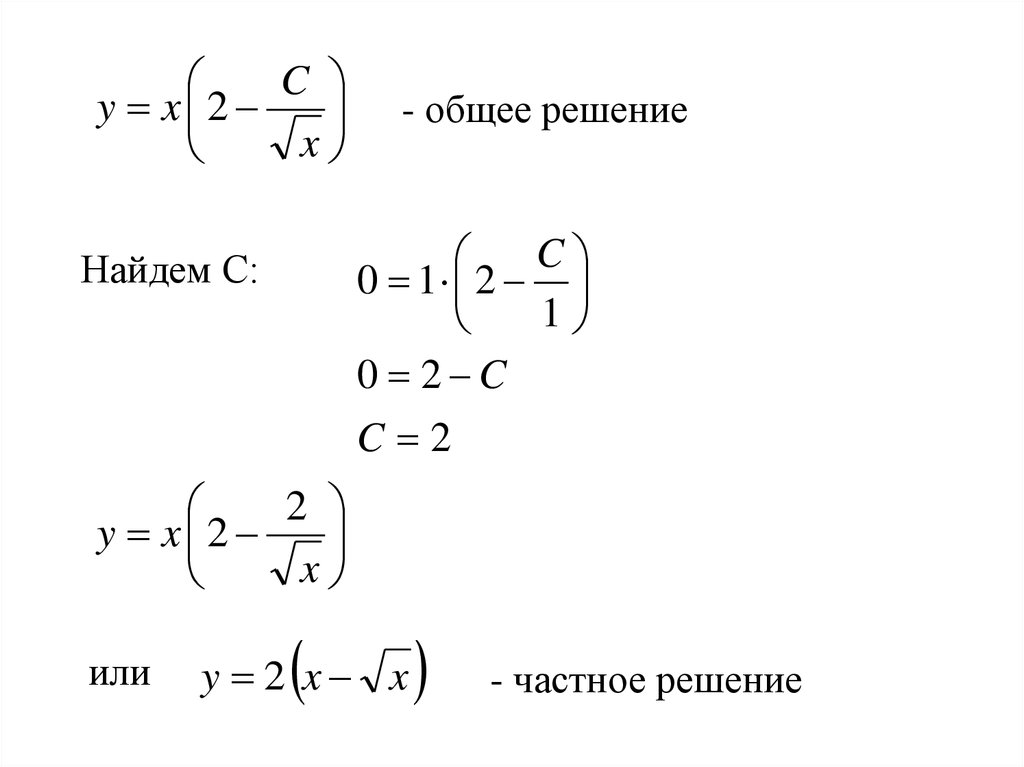


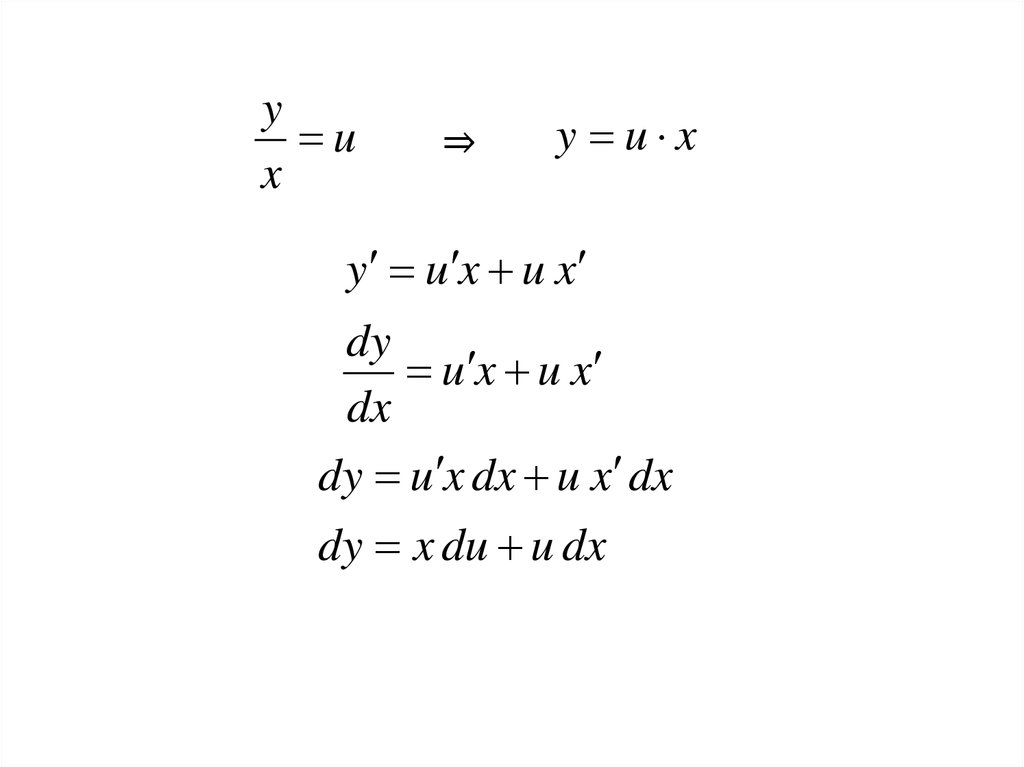
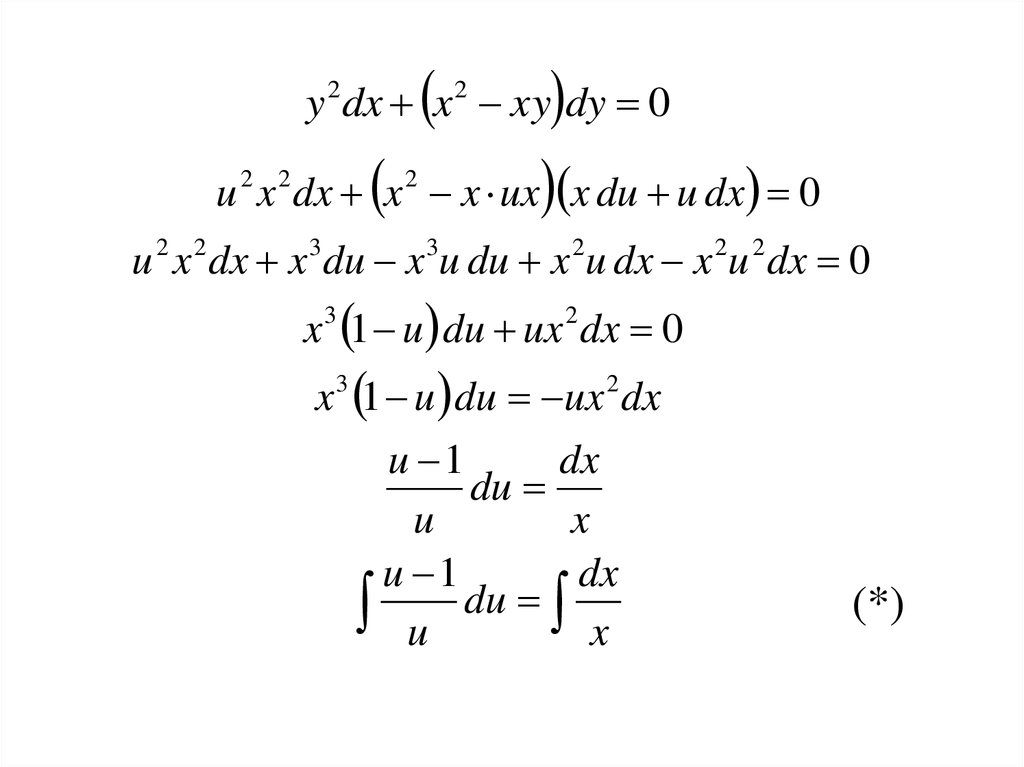


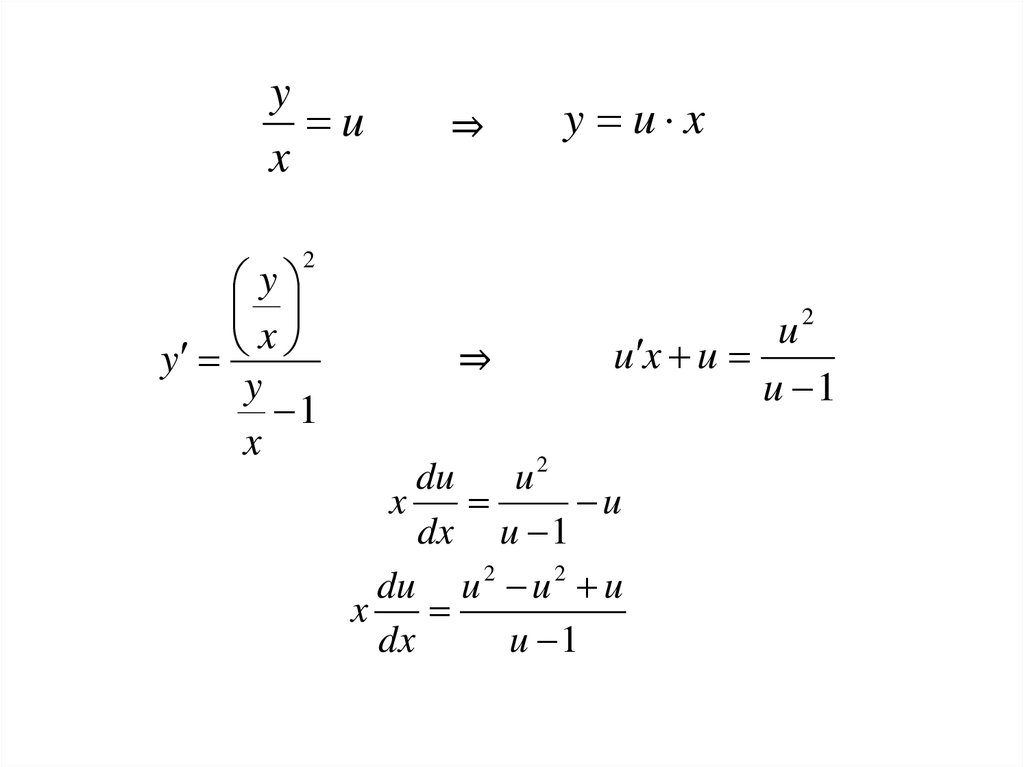




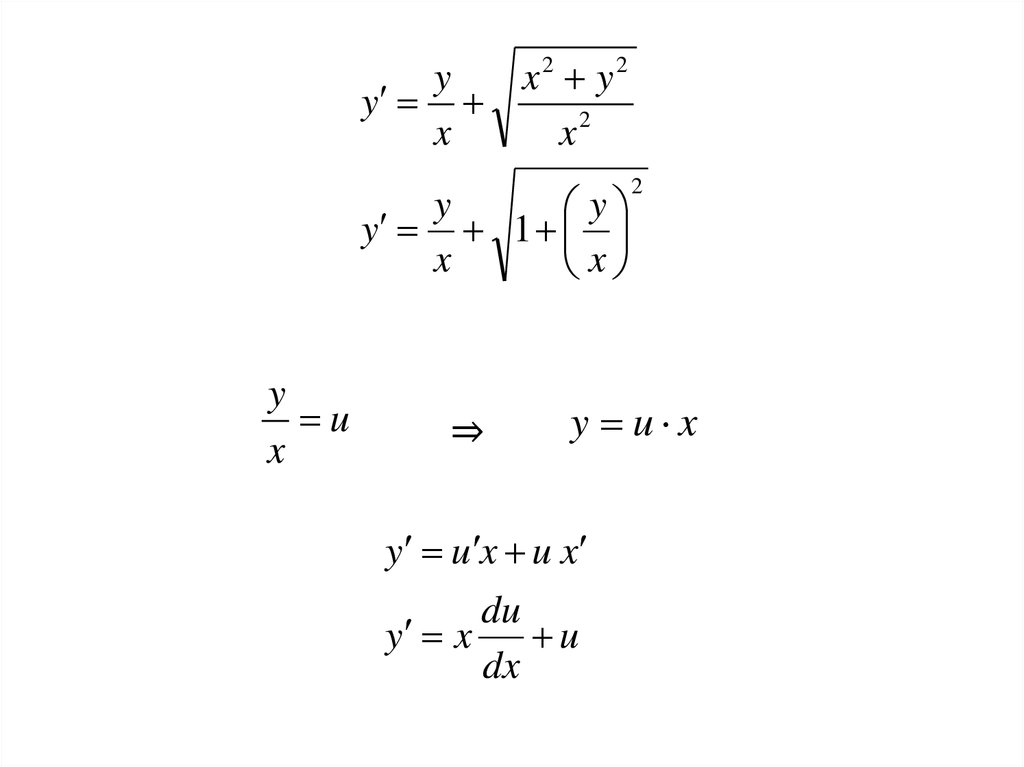


 Математика
Математика








