Похожие презентации:
Дифференциальные уравнения
1. Дифференциальные уравнения
Дифференциальныеуравнения первого порядка
Дифференциальные уравнения с
разделяющимися переменными
Однородные дифференциальные
уравнения
Линейные уравнения
2. Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является уравнениевида:
P ( x )dx Q( y )dy
(1)
Такое уравнение называется уравнением с разделенными
переменными.
Проинтегрировав это уравнение почленно, получим:
P ( x )dx Q( y )dy C - общий интеграл ДУ.
Более общий случай описывают уравнения с разделяющимися
переменными, которые имеют вид:
P1( x ) Q1( y )dx P2 ( x ) Q2 ( y )dy 0
(2)
Уравнение (2) сводится к уравнению (1) путем почленного
деления его на
P2 ( x ) Q1( y ) 0
3. Уравнения с разделяющимися переменными
Получаем:P1( x )
Q2 ( y )
dx
dy 0
P2 ( x )
Q1( y )
P1( x )
dx
P2 ( x )
Q2 ( y )
dy
Q1( y )
C
Замечание: при проведении почленного деления ДУ на
P2 ( x )Q1( y ) могут быть потеряны некоторые решения.
Поэтому следует отдельно решить уравнение P2 ( x )Q1( y ) 0
и установить те решения, которые не могут быть получены из
общего решения – особые решения.
Уравнение
y f1( x ) f2 ( y )
(3)
также сводится к уравнению с разделенными переменными.
dy
Для этого достаточно положить y
dx
dy
dy
f1( x ) f2 ( y )
f2 ( y )
dx
f ( x ) dx C
1
4. Уравнения с разделяющимися переменными
( y xy )dx ( x xy )dy 0y (1 x )dx x( y 1)dy
1 x
y 1
dx
dy
Разделим обе части уравнения на xy:
x
y
1
1
1
x dx 1 y dy x ln x y ln y C
Общий интеграл ДУ
Решим уравнение xy = 0:
Его решения: x = 0 и y = 0 являются решениями данного ДУ, но
не входят в общее решение, значит это особое решение.
y
y ; y ( 4) 1
x
dy
y
C
dy
dx
ln y ln x ln C ln y ln
dx
x
x
y
x
C
C
C 4
Подставим начальные условия: 1
y
4
4
x
y
Частное решение ДУ
Общее решение ДУ
x
Решить задачу Коши:
5. Уравнения с разделяющимися переменными
Рассмотрим задачу, приводящую к ДУ первого порядка сразделяющимися переменными:
Задача: материальная точка массы m замедляет свое движение
под воздействием силы сопротивления среды,
пропорциональной квадрату скорости V. Найти зависимость
скорости от времени. Найти скорость точки через 3 с после
начала замедления, если V(0) = 100 м/с, V(1) = 50 м/с.
Решение:
Примем за переменную время t, отсчитываемое от начала
замедления точки. Тогда скорость V будет функцией t: V = V(t).
Воспользуемся вторым законом Ньютона:
F m a F m V (t )
В нашем случае F kV 2
k 0 - коэффициент пропорциональности
6. Уравнения с разделяющимися переменными
Получим дифференциальное уравнение с разделяющимисяпеременными:
kV m V
2
1
k
t C
V
m
dV
k 2
V
dt
m
V
dV
2
V
k
m dt
1
k
t C
m
1
1
По условию задачи: V (0)
100 C
C
100
1
k
1
V (1)
50
k
1
m
100
m 100
100
Скорость точки изменяется по закону: V
V (3) 25
t 1
7. ДУ с однородной функцией нулевого порядка в правой части. (однородные уравнения первого порядка).
8.
Функция f(x;y) называется однородной
степени n, если умножение всех её
аргументов на одно и то же число t
равносильно умножению функции на tn, т.е.
f (tx; ty) t f ( x; y)
n
9. Пример 1.
f ( x; y) x 3 2 x 2 y 5 y 31)
- однородная функция
3-ей степени
f (tx; ty) tx 2 tx ty 5 ty
3
Так как
2
3
t x 2 t x t y 5 t y t x 2x y 5 y
3
3
2
2
3
3
3
3
2
3
t f ( x; y)
3
10.
2)f ( x; y ) 3x 2 y
Так как
3)
f (tx; ty) 3tx 2ty t 3x 2 y t f ( x; y)
x y
f ( x; y )
2x 3 y
Так как
- однородная функция 1-ой степени
- однородная функция 0-ой степени
tx ty
t x y
x y
f (tx; ty)
2tx 3ty t 2 x 3 y 2 x 3 y
f ( x; y) t 0 f ( x; y)
11.
4)y
f ( x; y ) x sin
x
2
Так как
5)
ty 2 2
y 2
f (tx; ty) tx sin t x sin t f ( x; y )
tx
x
2
1
f ( x; y )
x y
Так как
- однородная функция 2-ой степени
- однородная функция (-1)-ой степени
1
1 1
1
1
f (tx; ty)
t
tx ty t x y
x y
t 1 f ( x; y )
12.
ДУ I порядка y f ( x; y ) называется
однородным, если f(x;y)- однородная
функция 0-ой степени, т.е.
f (tx; ty) f ( x; y )
13.
Однородное ДУ I порядка y f ( x; y )можно записать в виде:
y
y
x
Т.к.
f ( x; y ) f (tx; ty)
, то если положить
1
t
x
Получаем:
x y
y
y
f ( x; y ) f ; f 1;
x x
x
x
14.
yРешение однородного ДУ I порядка y
x
Это уравнение преобразуется в уравнение с
разделяющимися переменными при помощи
замены переменной
y
u
x
или
y u x
15.
yy
x
y
u
x
u x u
u x u x u
u x u (u )
du
x
(u ) u
dx
du
dx
(u ) u x
или
y u x
16.
dudx
(u) u x
F (u) ln x C
или
y
F ln x C -общее решение данного ДУ
x
17. Пример 2. Найти общее решение ДУ:
yy
y tg
x
x
y
Это однородное ДУ вида y
x
y
u
x
⇒
y u x
18.
yy
y tg
x
x
u x u x u tgu
du
x u u tgu
dx
du
x tgu
dx
du dx
tgu x
19.
dudx
tgu x
ln sin u ln x C
ln sin u ln x ln C
ln sin u ln Cx
sin u Cx
sin u Cx
sin u Cx
u arcsin Cx
y
arcsin Cx
x
y x arcsin Cx
20. Пример 3. Решить задачу Коши: , если y(1)=0
Пример 3.Решить задачу Коши:
2x y
y
2x
, если y(1)=0
2x y 2x y
1 y
y
1
2x
2x 2x
2 x
y
Это однородное ДУ вида y
x
y
u
x
⇒
y u x
21.
1 yy 1
2 x
du
u
x
1
dx
2
1
u x u 1 u
2
du 2 u
x
dx
2
du
u
x
u 1
dx
2
du
u
x
1 u
dx
2
du
dx
2 u 2x
du
dx
2 u 2x
22.
1ln 2 u ln x C
2
2
2 ln 2 u ln x C
ln 2 u ln x ln C
2
C
ln 2 u ln
x
C
2
2 u
x
C
2 u
x
2
C
2 u
x
C
u 2
x
y
C
2
x
x
23.
Cy x 2
x
- общее решение
Решим задачу Коши
у(1)=0 :
C
0 1 2
1
0 2 C
C 2
2
y x 2
x
или
y 2 x x
- частное решение
24.
• Уравнение вида M ( x; y ) dx N ( x; y ) dy 0называется однородным уравнением в
дифференциальной форме,
если M(x;y) и N(x;y) - однородные
функции одной и той же степени.
25. Пример 4. Найти общее решение ДУ:
dydy
y x
xy
dx
dx
2
dy
dy
y x
xy
dx
dx
2
2
2
dx
y dx x dy xy dy
2
2
y dx x xy dy 0
2
M(x;y)
2
N(x;y)
- однородное уравнение вида
M ( x; y ) dx N ( x; y ) dy 0
26.
yu
x
⇒
y u x
y u x u x
dy
u x u x
dx
dy u x dx u x dx
dy x du u dx
27.
u x dx x x ux x du u dx 0y 2 dx x 2 xy dy 0
2
2
2
u x dx x du x u du x u dx x u dx 0
2
2
3
3
2
2
2
x 1 u du ux dx 0
3
2
x 1 u du ux dx
3
2
u 1
dx
du
u
x
u 1
dx
u du x
(*)
28.
dudx
du u x
u ln u ln x C
u ln u ln x ln C
ln eu ln u ln Cx
eu
ln
ln Cx
u
u
e
Cx
u
eu
Cx
u
eu uCx
y
x
y
e Cx
x
y
x
e Cy
- общее решение
29.
Это однородное ДУ можно привести к видуy
y
x
dy
dy
y x
xy
dx
dx
dy
2
2
y x xy
0
dx
x 2 xy y y 2
2
2
2
y
2
2
2
y
y
y
x
y
x x y x y x
y 1
2 y
x 1
x x
30.
yu
x
⇒
y u x
2
y
x
y
y
1
x
⇒
u2
u x u
u 1
du
u2
x
u
dx u 1
du u 2 u 2 u
x
dx
u 1
31.
duu
x
dx u 1
u 1
dx
du
u
x
u 1
dx
u du x
- получили (*)
32. Пример 5. Найти общее решение ДУ:
xx
2
2
2 y 2 dx 2 xy dy 0
M(x;y)
y
u
x
N(x;y)
⇒
y u x
y u x u x
2 y 2 dx 2 xy dy 0
- однородное уравнение вида
M ( x; y ) dx N ( x; y ) dy 0
dy
u x u x
dx
dy u x dx u x dx
dy x du u dx
33.
xx
dx 2 x u du 2 x u dx 0
2
2u 2 x 2 dx 2 x ux x du u dx 0
2
2 x 2u 2
3
2
2
x 2 dx 2 x 3u du 0
dx
2u du
x
dx
2u du x
u 2 ln x C
C
u ln
x
2
2
C
y
ln
x
x
C
2
2
y x ln
x
y 2 x 2 ln Cx
y 2 x 2 ln Cx 0
34. Пример 6. Найти общее решение ДУ:
22
xy y x y
Это однородное ДУ можно привести к виду
2
2
xy y x y
xy y x 2 y 2
2
2
x
y
y
y
x
x
:x
y
y
x
35.
yy
x y
x
x2
2
2
y
y
y 1
x
x
y
u
x
⇒
2
y u x
y u x u x
du
y x
u
dx
36.
dux
u u 1 u2
dx
du
x
1 u2
dx
du
dx
x
1 u2
du
dx
2
x
1 u
ln u 1 u 2 ln x C
u 1 u 2 Cx
y
y2
1 2 Cx
x
x
x2 y2
y
Cx
x
x
y x 2 y 2 Cx 2
общий интеграл ду
37.
y x 2 y 2 Cx 2- общий интеграл
или
x y Cx y
2
2
2
x y Cx y
2
2
2
2
2
x 2 y 2 Cx 4 2 yCx 2 y 2
x
2
x Cx
2
2
2 yC
1 C ( x 2 2 y)
1
C
2
x 2y
- общий интеграл
38.
Линейные уравненияпервого порядка
39. Линейные уравнения первого порядка
Линейным дифференциальным уравнением первого порядканазывается ДУ 1-го порядка, линейное относительно
неизвестной функции y и ее производной y .
В общем случае линейное уравнение 1-го порядка можно
записать в виде
где
y + p(x) y = q(x) ,
(1)
p(x) , q(x) – заданные непрерывные функции.
Если q(x) ≡ 0 , то линейное уравнение называется однородным.
В противном случае уравнение называется неоднородным.
Линейное однородное уравнение
y + p(x) y = 0
является уравнением с разделяющимися переменными.
40.
y p(x) y 0Разделим переменные:
dy
p( x)dx,
dy
p( x) y 0
dx
интегрируя это выражение, получаем:
y
ln y p( x)dx ln C, где C 0
ln y ln e p( x)dx lnC, где C 0
p( x)dx
y Ce
,
C 0
В процессе преобразований было потеряно решение y=0.
Тогда общее решение принимает вид:
p( x)dx
y C e
,
C.
(2)
41. Рассмотрим линейное неоднородное уравнение:
y + p(x) y = f(x) .Существуют два метода его интегрирования.
(1)
I)Метод
вариации постоянной
(метод Лагранжа)
1) Интегрируем однородное уравнение y + p(x) y = 0,
– соответствующее данному неоднородному уравнению.
Его общее решение имеет вид :
(2)
y C e
p( x)dx
.
2) Полагаем, что решение неоднородного уравнения по
структуре совпадает с решением соответствующего линейного
однородного уравнения.
p( x)dx
Оно имеет вид y C(x) e
.
Функцию C(x) найдем, подставив
у и y в исходное неоднородное уравнение
(1).
42. C( x) e p( x)dx
ey C( x)x)dx
p(
p( x)dx
dy dC p( x)dx
C(
x)
p( x)
e
e
dx dx
Подставим эти выражения в уравнение y p( x) y f (x) :
p( x)dx
p( x)dx
dC p( x)dx
e
C(
x)
e
p(
x)
p(
x)
C(
x)
e
f (x)
dx
dC e p( x)dx f (x)
dx
dC
p( x)dx
f
(x)
e
dx
dC f (x) e
p( x)dx
Интегрируя, находим
dx
C(x) f (x) e
p( x)dx
dx C .
43. C(x) f (x) e p(x)dx dx C .
p(x)dxC(x) f (x) e
dx C .
Таким образом, общее решение линейного неоднородного
уравнения (1) имеет вид:
p( x)dx
p( x)dx
p( x)dx
y C( x) e
f (x) e
dx C )e
Замечание.
Раскроем скобки в (3):
y(x) C e p( x)dx e p( x)dx f (x) e p( x)dxdx .
(3)
(4)
Заметим, что первое слагаемое в (4) – общее решение
линейного однородного уравнения, а второе – частное
решение линейного неоднородного уравнения (получается из
общего решения при C = 0).
44.
II) Метод Бернулли.Будем искать решение (1) в следующем виде:
y = u(x) v(x) .
Тогда
y =u v+u v .
Подставим
и
y
в уравнение (1)
y
и получим:
u v + u v + puv = f(x)
или
u v + u [ v + pv ] = f(x) .
Полагаем, что функция v(x) такова, что
[ v + pv ] = 0 .
(5)
Тогда
u v = f(x) .
Условия (5) позволяют однозначно определить v(x) и u(x) .
Первое уравнение – это линейное однородное уравнение
v(x) Ce
p( x)dx
45.
Учитывая свободу выбора v(x), положим С = 1, тогдаp( x)dx
v( x) e
.
Подставляем полученную функцию во второе уравнение:
du p( x)dx
p( x)dx
e
f (x)
du
f
(x)
e
dx
dx
u( x) f (x) e
y u( x) v( x) e
p( x)dx
p(x)dx
dx C
p(x)dx
dx C .
f (x) e
Замечание. Линейное неоднородное уравнение вида
y + p(x) y = b
проще интегрировать как уравнение с разделяющимися
переменными.














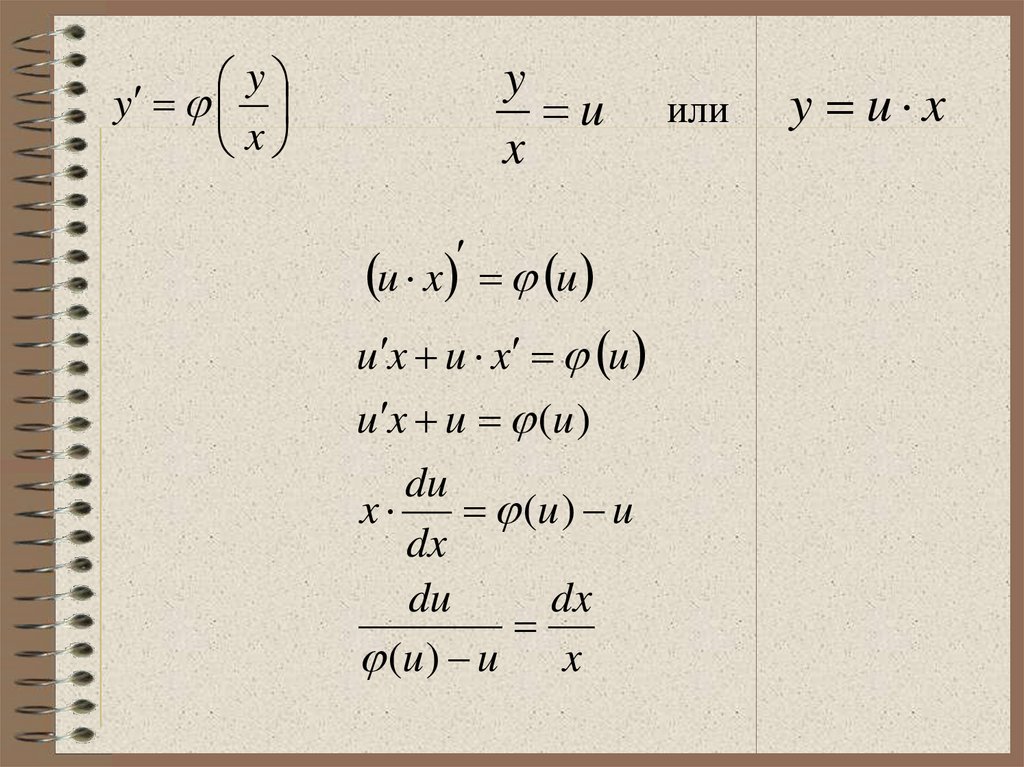



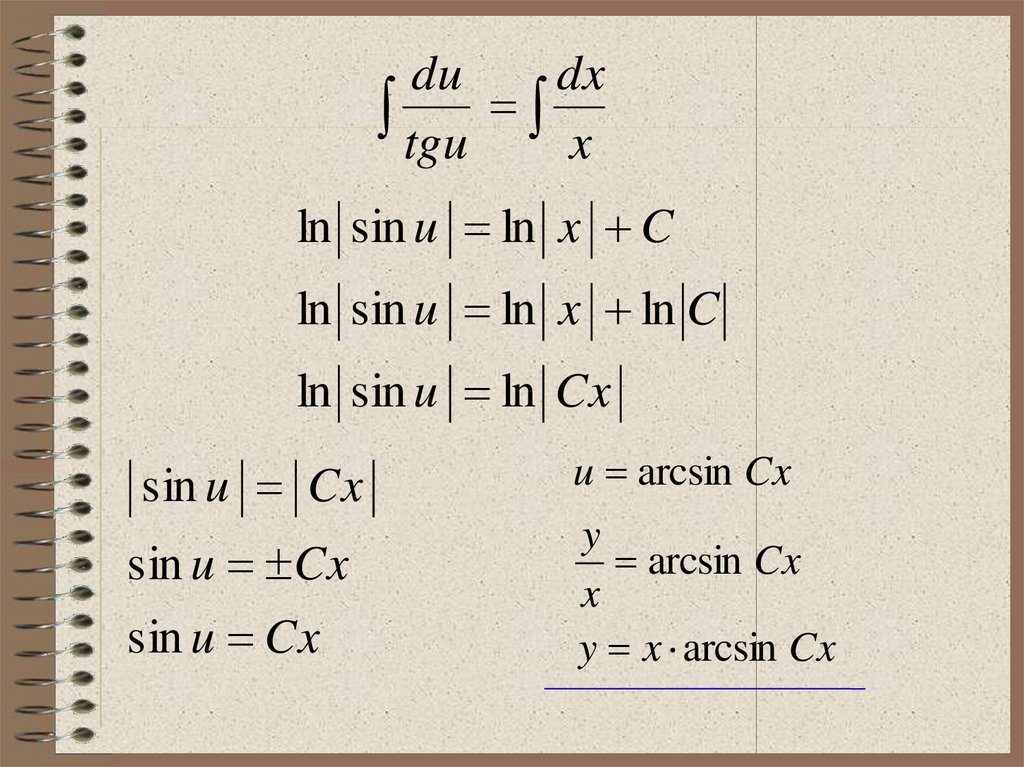

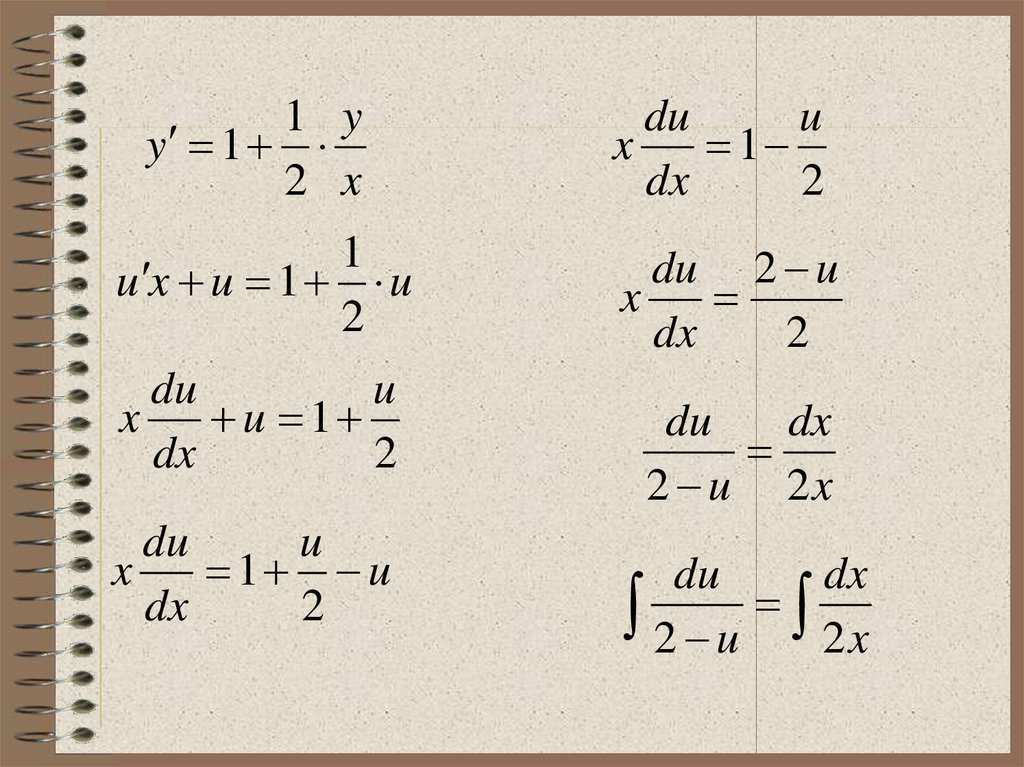
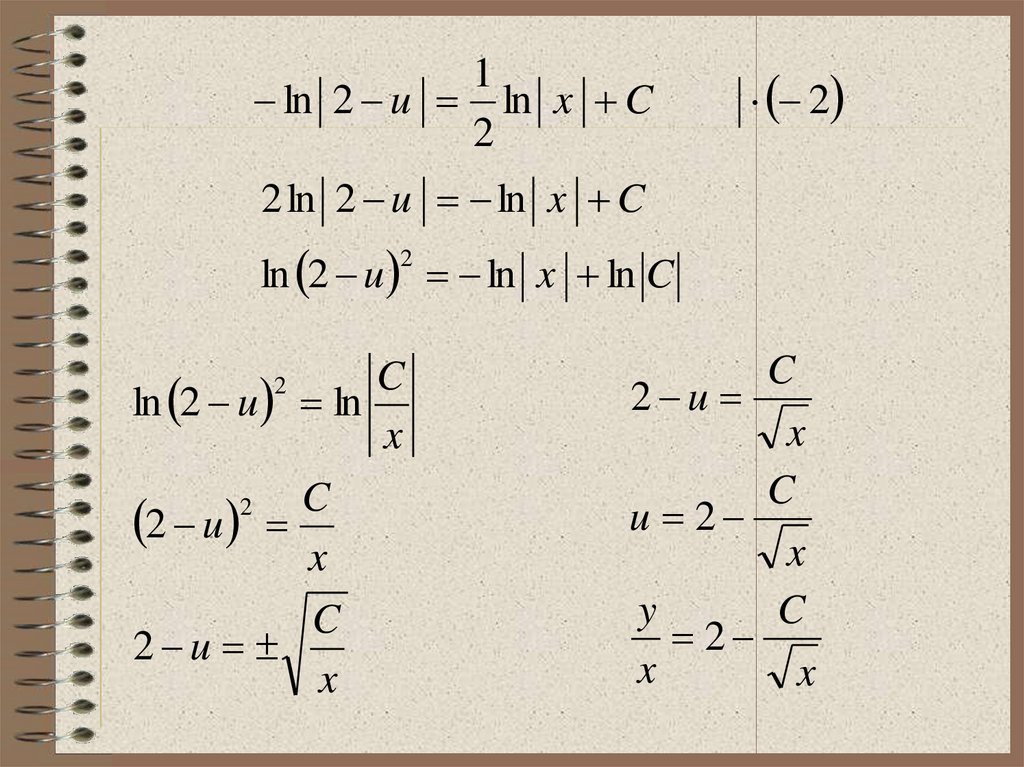







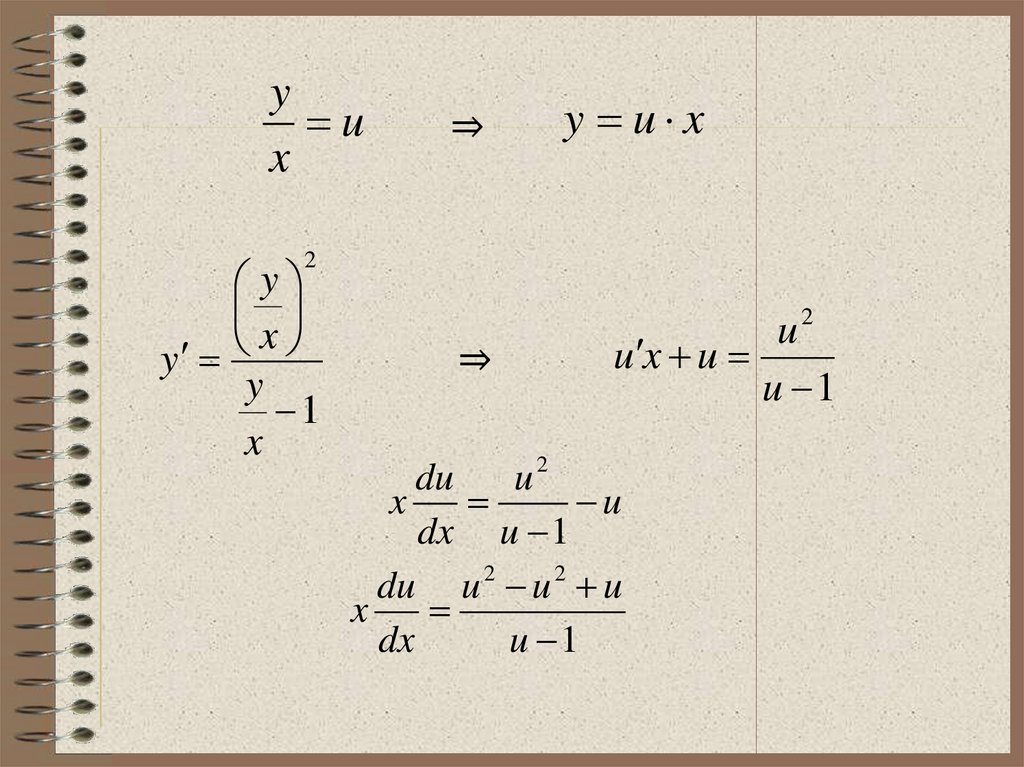


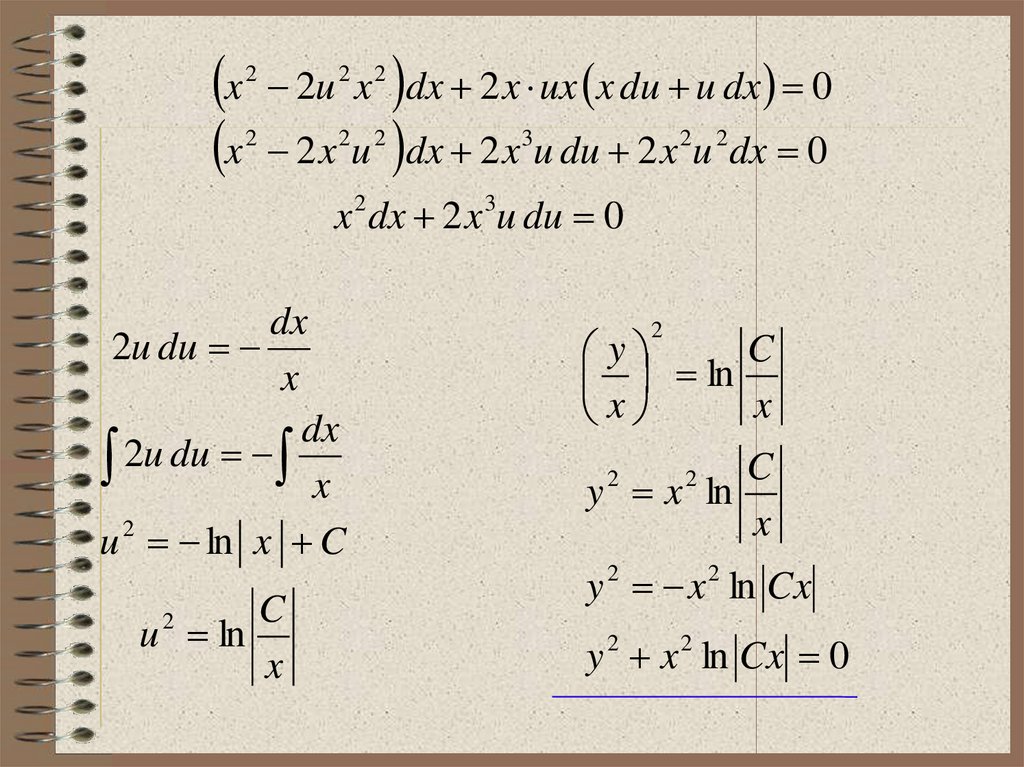












 Математика
Математика








