Кинематика сейсмических волн

1. КИНЕМАТИКА СЕЙСМИЧЕСКИХ ВОЛН

2. КИНЕМАТИКА ВОЛН В МНГОСЛОЙНЫХ СРЕДАХ

3. ОТРАЖЕННЫЕ ВОЛНЫ

4.

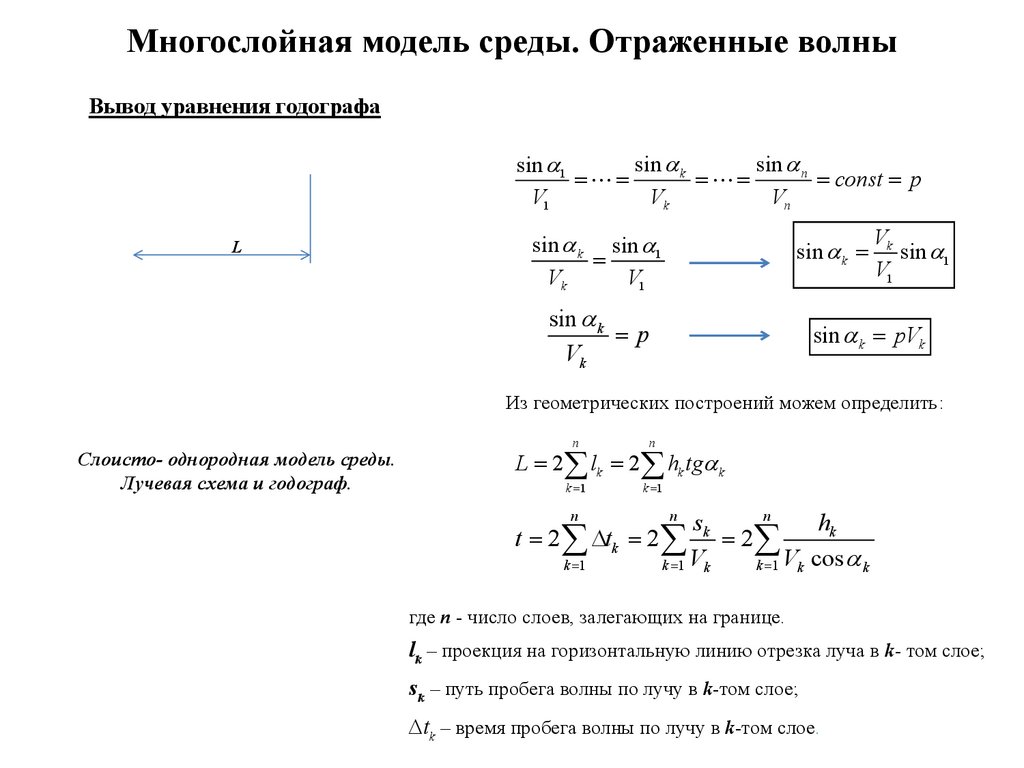
Многослойная модель среды. Отраженные волны
Вывод уравнения годографа
sin k
sin n
sin 1
const p
V1
Vk
Vn
L
sin k sin 1
Vk
V1
sin k
sin k
p
Vk
Vk
sin 1
V1
sin k pVk
Из геометрических построений можем определить:
Слоисто- однородная модель среды.
Лучевая схема и годограф.
n
n
k 1
k 1
L 2 lk 2 hk tg k
n
sk
hk
t 2 tk 2 2
k 1
k 1 Vk
k 1 Vk cos k
n
n
где n - число слоев, залегающих на границе.
lk – проекция на горизонтальную линию отрезка луча в k- том слое;
sk – путь пробега волны по лучу в k-том слое;
∆tk – время пробега волны по лучу в k-том слое.

5.

Многослойная модель среды. Отраженные волны
Вывод уравнения годографа
Если в качестве параметра использовать лучевой параметр р:
pVk
tg k
sin k pVk
cos k 1 p 2Vk2
1 p 2Vk2
Уравнение годографа отраженной волны :
L
n
L 2
phk Vk
2 2
k 1 1 p k Vk
n
t 2
k 1Vk
hk
1 p k2Vk2
Если в качестве параметра использовать угол 1
между лучом и вертикалью в первом слое:
Слоисто-однородная модель среды.
Лучевая схема и годограф.
n
L 2 hk tg k
sin k
V
1
2
2
cos a k 1 ( k sin 2 a k ) 2
V1 Vk sin 2 a1
V1
V1
tga k
k 1
hk
t 2
k 1 Vk cos k
n
Vk
sin 1
V1
Vk sin a1
V12 Vk2 sin 2 a1
Уравнение годографа отраженной волны :
n
hk Vk sin 1
k 1
V12 Vk2 sin 2 1
L 2
n
t 2
k 1Vk
hk V1
V12 Vk2 sin 2 1

6.

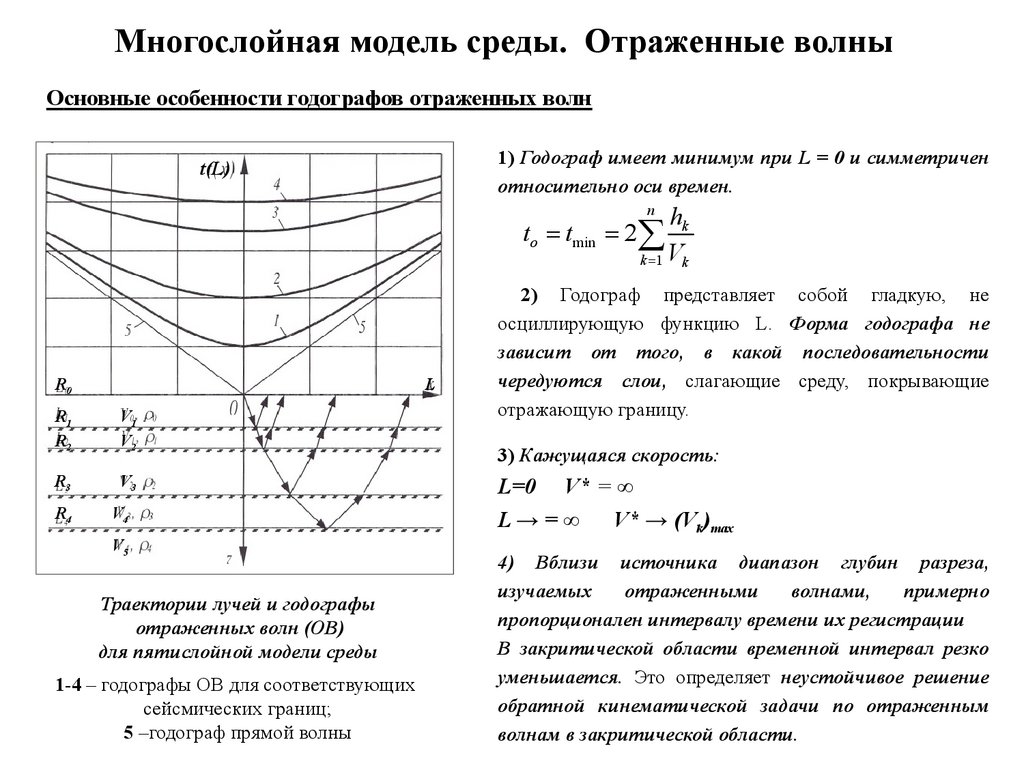
Многослойная модель среды. Отраженные волны
Основные особенности годографов отраженных волн
1) Годограф имеет минимум при L = 0 и симметричен
относительно оси времен.
t(L)
n
h
to tmin 2 k
k 1 Vk
L
R0
R1
R2
V1
V2
R3
V3
R4
V4
V5
Траектории лучей и годографы
отраженных волн (ОВ)
для пятислойной модели среды
1-4 – годографы ОВ для соответствующих
сейсмических границ;
5 –годограф прямой волны
2) Годограф представляет собой гладкую, не
осциллирующую функцию L. Форма годографа не
зависит от того, в какой последовательности
чередуются слои, слагающие среду, покрывающие
отражающую границу.
3) Кажущаяся скорость:
L=0 V* = ∞
L → = ∞ V* → (Vk)max
4) Вблизи источника диапазон глубин разреза,
изучаемых
отраженными
волнами,
примерно
пропорционален интервалу времени их регистрации
В закритической области временной интервал резко
уменьшается. Это определяет неустойчивое решение
обратной кинематической задачи по отраженным
волнам в закритической области.

7.

Многослойная модель среды. Отраженные волны
Основные особенности годографов отраженных волн
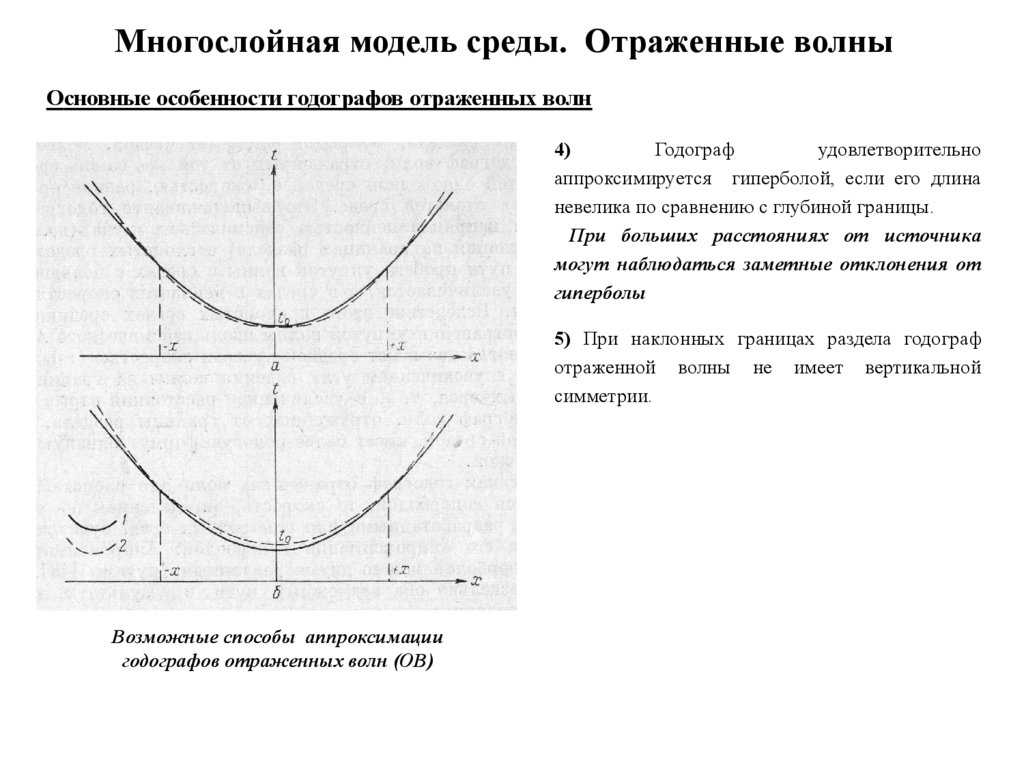
4)
Годограф
удовлетворительно
аппроксимируется гиперболой, если его длина
невелика по сравнению с глубиной границы.
При больших расстояниях от источника
могут наблюдаться заметные отклонения от
гиперболы
5) При наклонных границах раздела годограф
отраженной волны не имеет вертикальной
симметрии.
Возможные способы аппроксимации
годографов отраженных волн (ОВ)

8. ГОЛОВНЫЕ ВОЛНЫ

9.

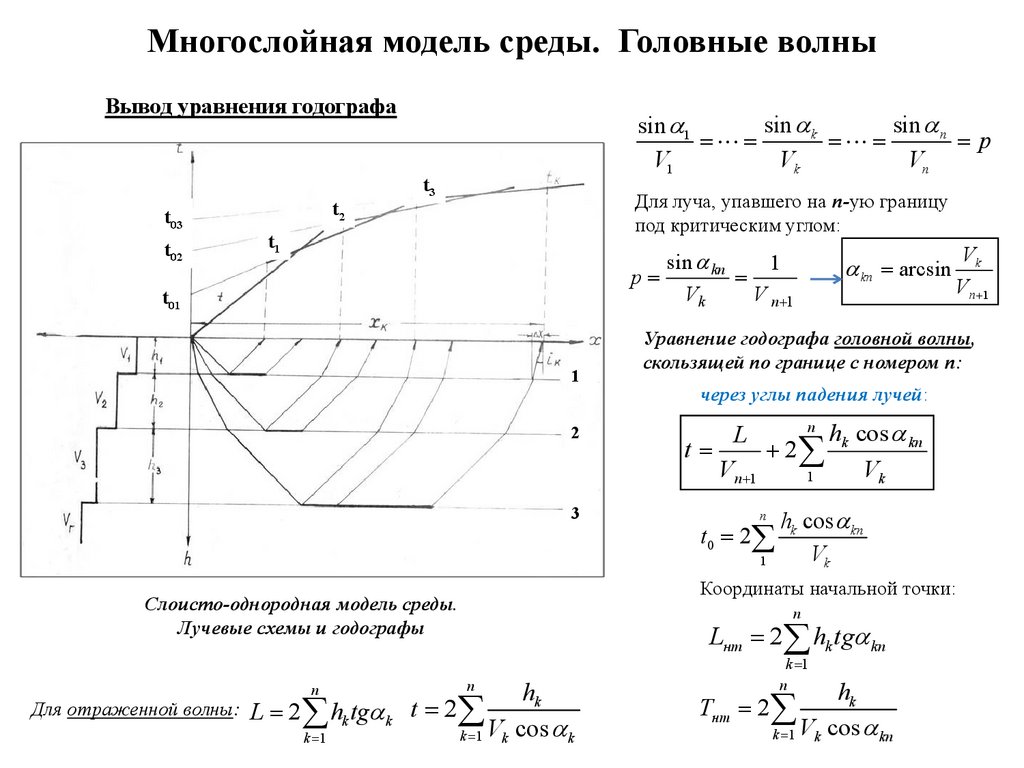
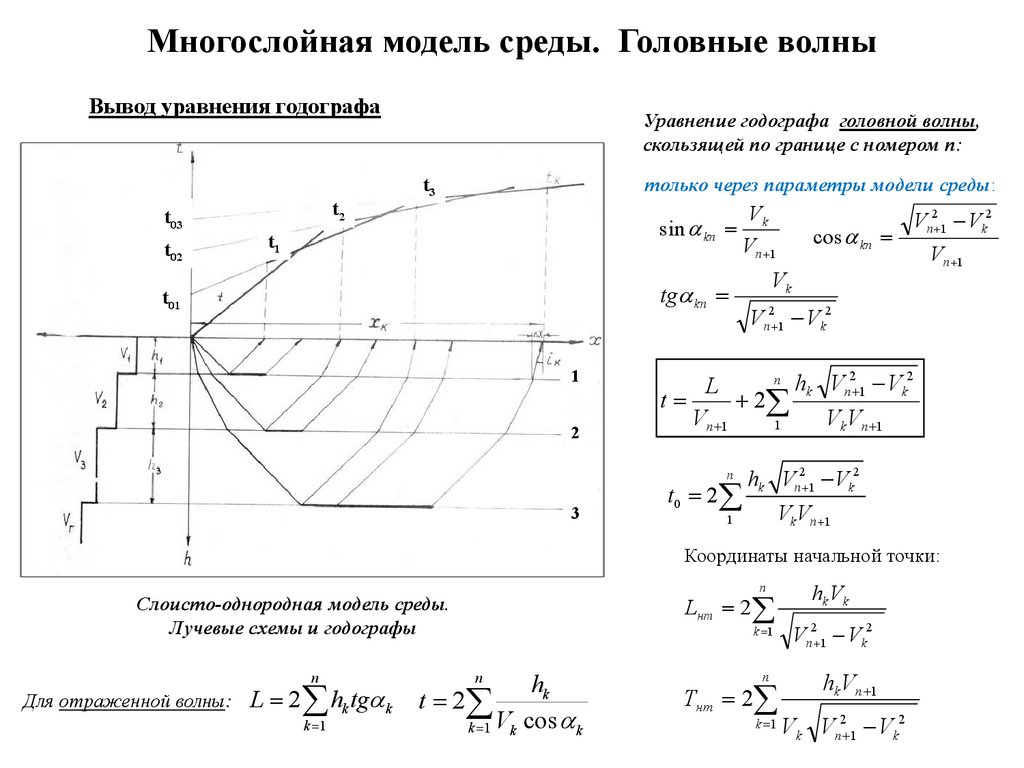
Многослойная модель среды. Головные волны
Вывод уравнения годографа
t03
t02
t2
sin k
sin n
sin 1
p
V1
Vk
Vn
t3
Для луча, упавшего на n-ую границу
под критическим углом:
t1
sin kn
1
p
Vk
V n 1
t01
1
2
3
Для отраженной волны: L 2
Уравнение годографа головной волны,
скользящей по границе с номером n:
через углы падения лучей:
n
h cos kn
L
t
2 k
Vn 1
Vk
1
h cos kn
t 0 2 k
Vk
1
n
n
Lнт 2 hk tg kn
hk
k 1 Vk cos k
n
hk tg k t 2
k 1
Vk
Vn 1
Координаты начальной точки:
Слоисто-однородная модель среды.
Лучевые схемы и годографы
n
kn arcsin
k 1
n
hk
k 1 Vk cos kn
Tнт 2

10.

Многослойная модель среды. Головные волны
Вывод уравнения годографа
t03
t02
t2
Уравнение годографа головной волны,
скользящей по границе с номером n:
t3
только через параметры модели среды:
sin kn
t1
Vk
Vn 1
tg kn
t01
1
2
3
cos kn
Vn2 1 Vk2
Vk
Vn 1
Vn2 1 Vk2
2
2
n h
L
k Vn 1 Vk
t
2
Vn 1
Vk Vn 1
1
n
hk Vn2 1 Vk2
1
VkVn 1
t 0 2
Координаты начальной точки:
n
Для отраженной волны:
L 2 hk tg k
k 1
n
hk Vk
k 1
Vn2 1 Vk2
n
hk Vn 1
k 1
Vk Vn2 1 Vk2
Lнт 2
Слоисто-однородная модель среды.
Лучевые схемы и годографы
hk
t 2
k 1 Vk cos k
n
Tнт 2

11.

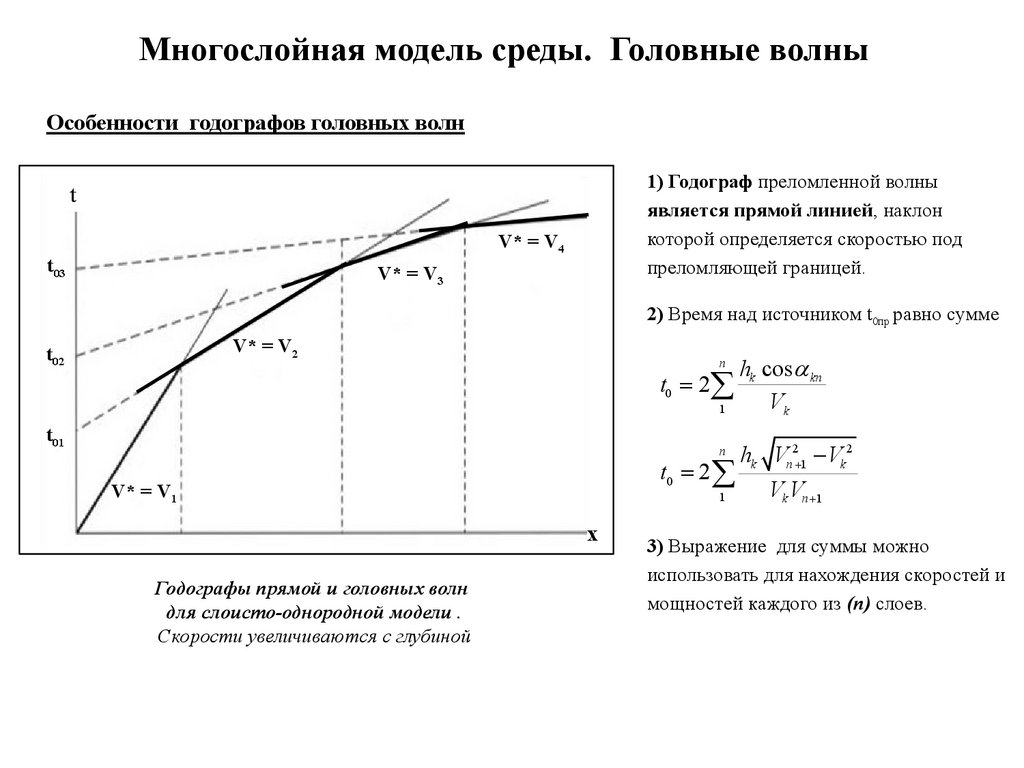
Многослойная модель среды. Головные волны
Особенности годографов головных волн
1) Годограф преломленной волны
является прямой линией, наклон
которой определяется скоростью под
преломляющей границей.
t
V* = V4
t03
V* = V3
2) Время над источником t0пр равно сумме
V* = V2
t02
h cos kn
t0 2 k
Vk
1
n
t01
hk Vn2 1 Vk2
t0 2
Vk Vn 1
1
n
V* = V1
x
Годографы прямой и головных волн
для слоисто-однородной модели .
Скорости увеличиваются с глубиной
3) Выражение для суммы можно
использовать для нахождения скоростей и
мощностей каждого из (n) слоев.

12.

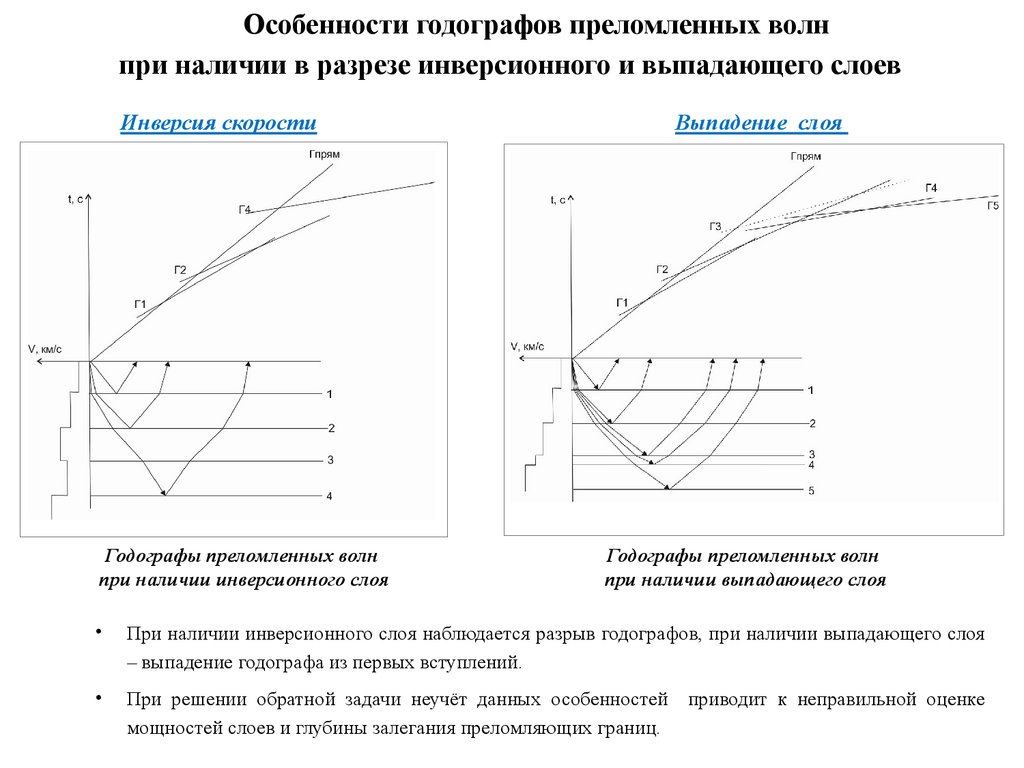
Особенности годографов преломленных волн
при наличии в разрезе инверсионного и выпадающего слоев
Инверсия скорости
Годографы преломленных волн
при наличии инверсионного слоя
Выпадение слоя
Годографы преломленных волн
при наличии выпадающего слоя
При наличии инверсионного слоя наблюдается разрыв годографов, при наличии выпадающего слоя
– выпадение годографа из первых вступлений.
При решении обратной задачи неучёт данных особенностей
мощностей слоев и глубины залегания преломляющих границ.
приводит к неправильной оценке

13.

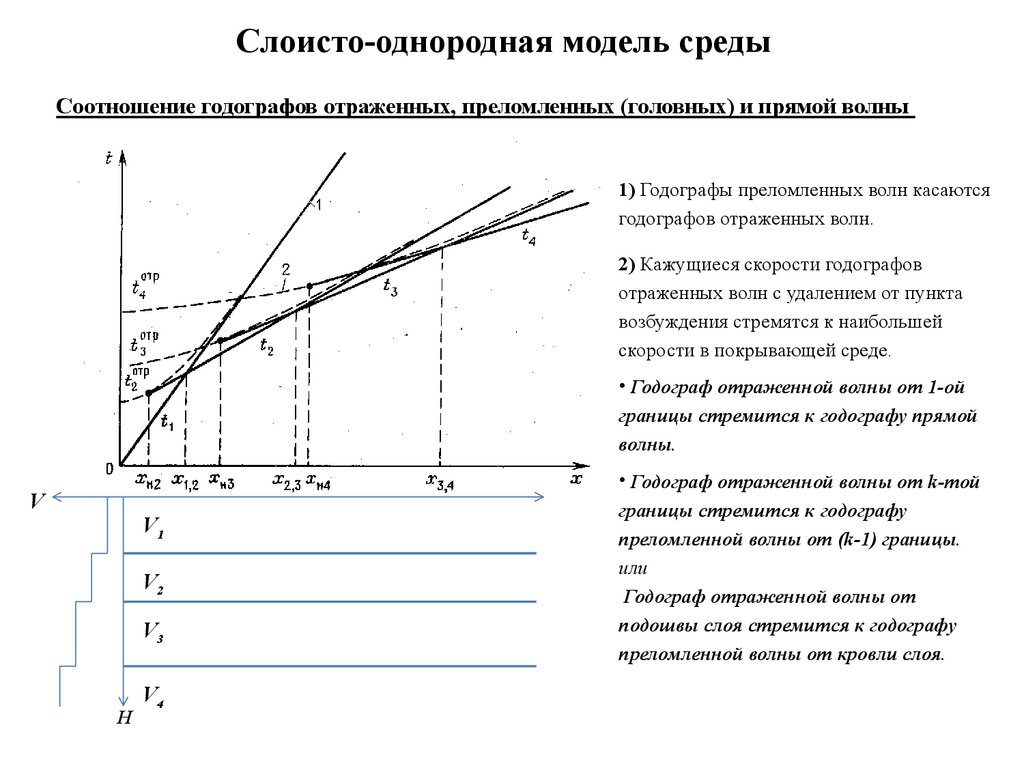
Слоисто-однородная модель среды
Соотношение годографов отраженных, преломленных (головных) и прямой волны
1) Годографы преломленных волн касаются
годографов отраженных волн.
2) Кажущиеся скорости годографов
отраженных волн с удалением от пункта
возбуждения стремятся к наибольшей
скорости в покрывающей среде.
• Годограф отраженной волны от 1-ой
границы стремится к годографу прямой
волны.
V
V1
V2
V3
H
V4
• Годограф отраженной волны от k-той
границы стремится к годографу
преломленной волны от (k-1) границы.
или
Годограф отраженной волны от
подошвы слоя стремится к годографу
преломленной волны от кровли слоя.

14. РЕФРАГИРОВАННЫЕ ВОЛНЫ

15.

Непрерывная градиентная среда
Луч с параметром p, выходящий на линию
наблюдения на удалении L, не может проникнуть на
глубину, превышающую предельное значение Zmax,
zmax
где выполняется условие :
Sin 0
1
1
p *
V (0) V ( zmax )
V
z
Образуется только рефрагированная волна.
Лучевая схема и годограф рефрагированной
волны
Уравнение годографа рефрагированной волны:
Z max
L 2
0
Уравнение годографа отраженной волны
в случае однородно-слоистой модели:
n
L 2
phk Vk
2 2
k 1 1 p k Vk
n
t 2
k 1Vk
Z max
t 2
0
hk
1 p k2Vk2
pV ( z )
1 p V ( z)
2
dz
2
1
V ( z) 1 p V ( z)
2
2
dz

16.

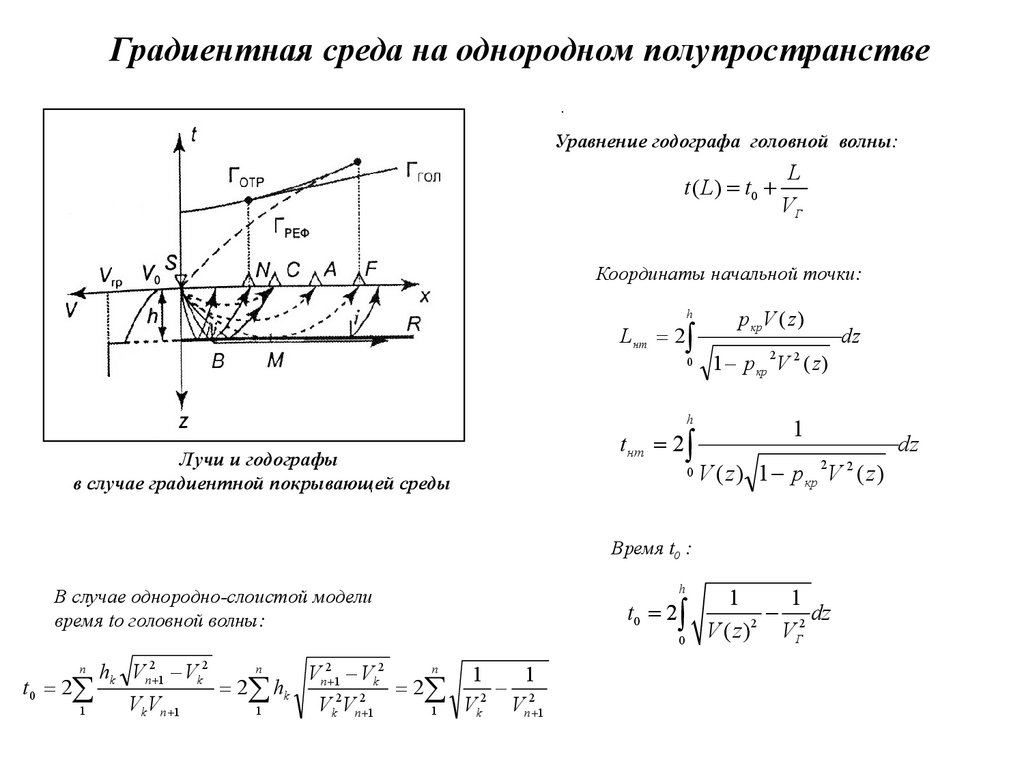
Градиентная среда на однородном полупространстве
.
Образуются три волны:
• рефрагированная,
• отраженная ,
• головная.
Уравнение годографа рефрагированной волны:
Z max
L 2
0
pV ( z )
1 p V ( z)
2
Z max
t 2
0
dz
2
1
V ( z) 1 p V ( z)
2
dz
2
Уравнение годографа отраженной волны:
Лучи и годографы
в случае градиентной покрывающей среды
h
L 2
0
Уравнение годографа отраженной волны
в случае однородно-слоистой модели:
n
L 2
phk Vk
2 2
k 1 1 p k Vk
n
t 2
hk
2 2
k 1Vk 1 p k Vk
h
t 2
0
pV ( z )
1 p V ( z)
2
dz
2
1
V ( z) 1 p V ( z)
2
h
2
dz
2h
V ( z)
V
0
t0 2
dz

17.

Градиентная среда на однородном полупространстве
.
Уравнение годографа головной волны:
t ( L ) t0
L
VГ
Координаты начальной точки:
h
Lнт 2
0
h
Лучи и годографы
в случае градиентной покрывающей среды
t нт 2
0
p крV ( z )
2
dz
1 p кр V ( z )
2
1
dz
2
V ( z ) 1 p кр V ( z )
Время t0 :
В случае однородно-слоистой модели
время tо головной волны:
h
t0 2
0
n
hk Vn2 1 Vk2
1
Vk Vn 1
t 0 2
n
2 hk
1
n
Vn2 1 Vk2
1
1
2
Vk2Vn2 1
Vk2 Vn2 1
1
1
1
dz
2
2
V ( z ) VГ
2

18.

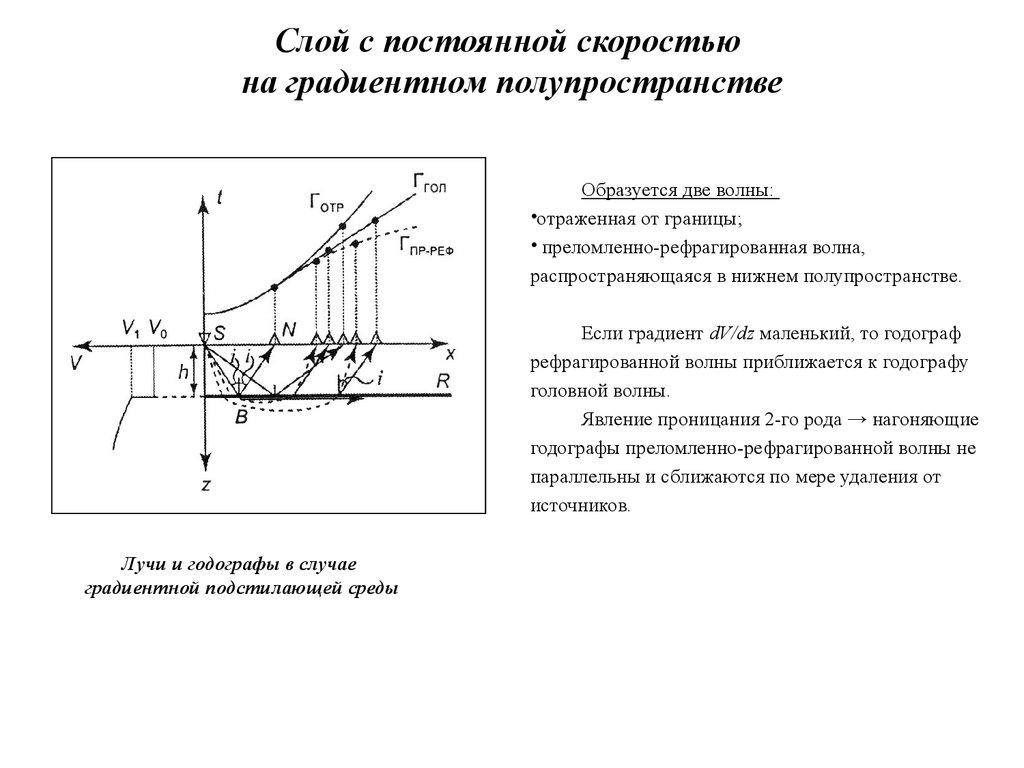
Слой с постоянной скоростью
на градиентном полупространстве
Образуется две волны:
•отраженная от границы;
• преломленно-рефрагированная волна,
распространяющаяся в нижнем полупространстве.
Если градиент dV/dz маленький, то годограф
рефрагированной волны приближается к годографу
головной волны.
Явление проницания 2-го рода → нагоняющие
годографы преломленно-рефрагированной волны не
параллельны и сближаются по мере удаления от
источников.
Лучи и годографы в случае
градиентной подстилающей среды

19.

20.

21.

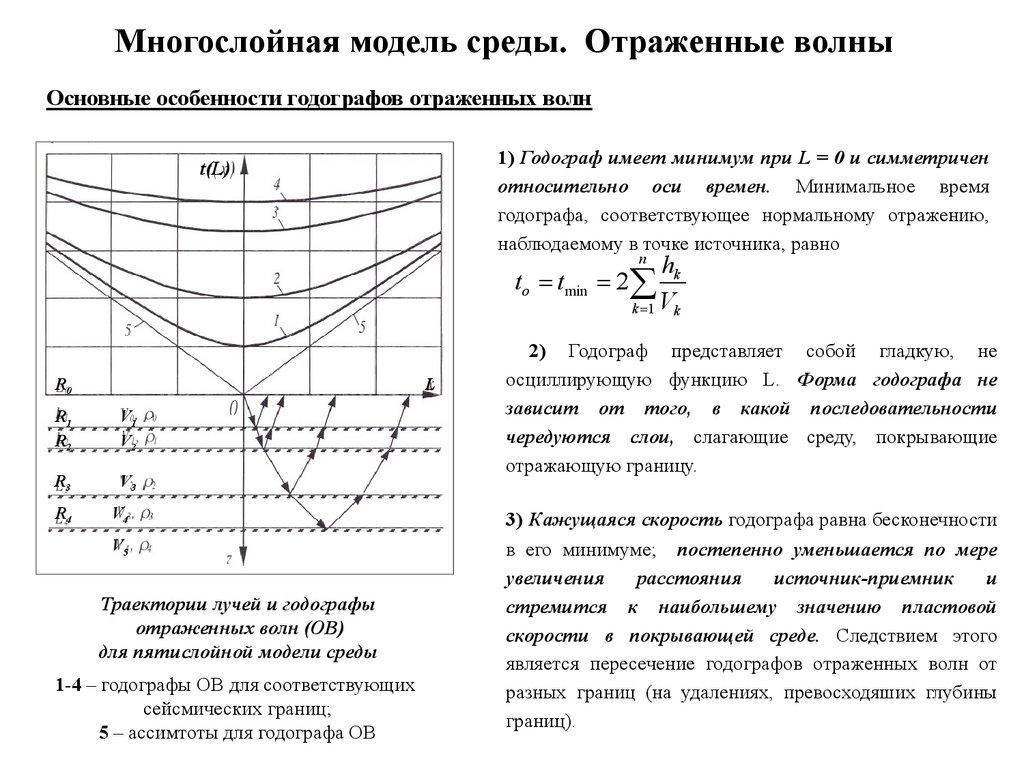
Многослойная модель среды. Отраженные волны
Основные особенности годографов отраженных волн
1) Годограф имеет минимум при L = 0 и симметричен
относительно оси времен. Минимальное время
годографа, соответствующее нормальному отражению,
наблюдаемому в точке источника, равно
t(L)
n
h
to tmin 2 k
k 1 Vk
L
R0
R1
R2
V1
V2
R3
V3
R4
V4
V5
Траектории лучей и годографы
отраженных волн (ОВ)
для пятислойной модели среды
1-4 – годографы ОВ для соответствующих
сейсмических границ;
5 – ассимтоты для годографа ОВ
2) Годограф представляет собой гладкую, не
осциллирующую функцию L. Форма годографа не
зависит от того, в какой последовательности
чередуются слои, слагающие среду, покрывающие
отражающую границу.
3) Кажущаяся скорость годографа равна бесконечности
в его минимуме; постепенно уменьшается по мере
увеличения
расстояния
источник-приемник
и
стремится к наибольшему значению пластовой
скорости в покрывающей среде. Следствием этого
является пересечение годографов отраженных волн от
разных границ (на удалениях, превосходяших глубины
границ).

22.

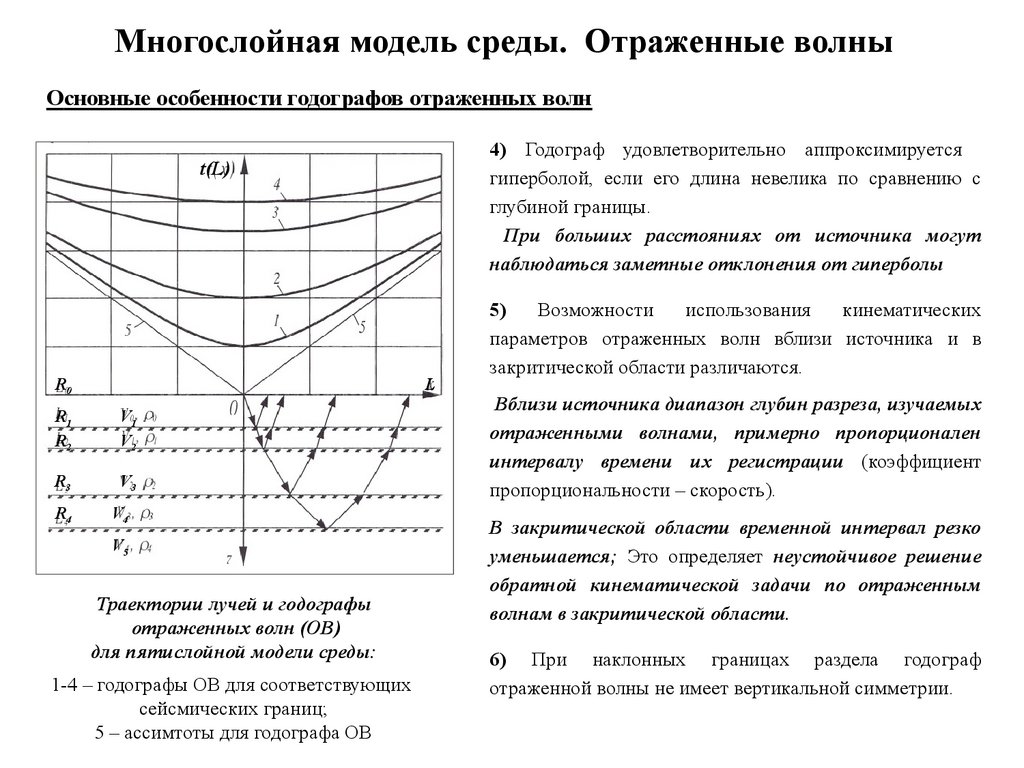
Многослойная модель среды. Отраженные волны
Основные особенности годографов отраженных волн
4) Годограф удовлетворительно аппроксимируется
гиперболой, если его длина невелика по сравнению с
глубиной границы.
При больших расстояниях от источника могут
наблюдаться заметные отклонения от гиперболы
t(L)
L
R0
R1
R2
V1
V2
R3
V3
R4
V4
V5
Траектории лучей и годографы
отраженных волн (ОВ)
для пятислойной модели среды:
1-4 – годографы ОВ для соответствующих
сейсмических границ;
5 – ассимтоты для годографа ОВ
5)
Возможности
использования
кинематических
параметров отраженных волн вблизи источника и в
закритической области различаются.
Вблизи источника диапазон глубин разреза, изучаемых
отраженными волнами, примерно пропорционален
интервалу времени их регистрации (коэффициент
пропорциональности – скорость).
В закритической области временной интервал резко
уменьшается; Это определяет неустойчивое решение
обратной кинематической задачи по отраженным
волнам в закритической области.
6) При наклонных границах раздела годограф
отраженной волны не имеет вертикальной симметрии.

23.

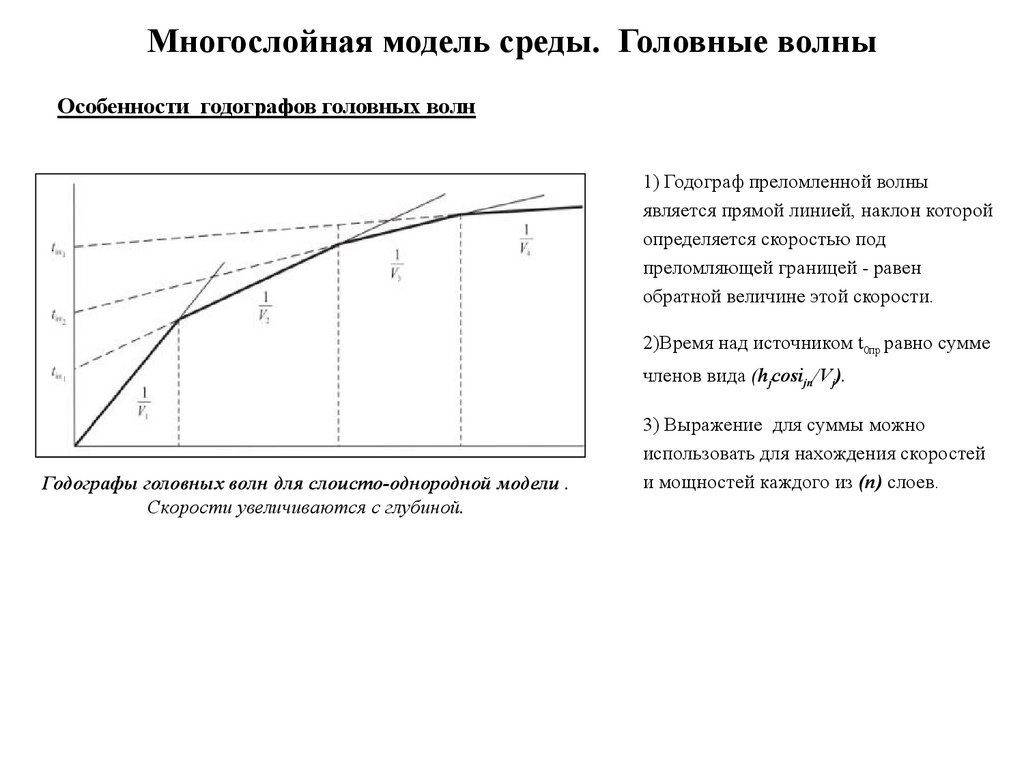
Многослойная модель среды. Головные волны
Особенности годографов головных волн
1) Годограф преломленной волны
является прямой линией, наклон которой
определяется скоростью под
преломляющей границей - равен
обратной величине этой скорости.
2)Время над источником t0пр равно сумме
членов вида (hjcosijn/Vj).
Годографы головных волн для слоисто-однородной модели .
Скорости увеличиваются с глубиной.
3) Выражение для суммы можно
использовать для нахождения скоростей
и мощностей каждого из (n) слоев.