Похожие презентации:
Кинематика материальной точки
1. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.КИНЕМАТИКА
ЛЕКЦИЯ 1
2. План лекции
ВведениеСпособы задания движения
Скорость
Ускорение
Частные случаи движения
Заключение
2
3. Введение
Мы изучили первый раздел курса ТМ - СТАТИКУ.F1
F2
Основной результат
ТЕЛО, СИЛЫ : ( F1 ,..., F1 )
n
n
( F1 ,..., F1 ) 0 Fk 0, M 0 Fk 0
k 1
F3
Fn
k 1
Если уравнения равновесия не выполнены, то тело будет двигаться!
Каким образом?
Ответ на этот вопрос будет дан в третьей части курса – в динамике.
Вторая часть курса – кинематика, нужна для того, чтобы разобраться с
самим движением.
Причины движения (т.е. СИЛЫ) нас в кинематике интересовать не
будут!
3
Кинематика
4. КИНЕМАТИКА
наука, изучающая движение телбез учета действующих на них сил.
Задачи кинематики:
1. Научиться задавать движение тел
2. По заданным законам движения тел определять их
кинематические характеристики
(скорость, ускорение, …)
Замечание. Есть еще и обратная задача - по заданным кинематическим
характеристикам тела определять закон его движения.
Решать эти задачи мы начнем с простейшего тела –
материальной точки.
Цель лекции: изучить кинематику точки.
4
Кинематика
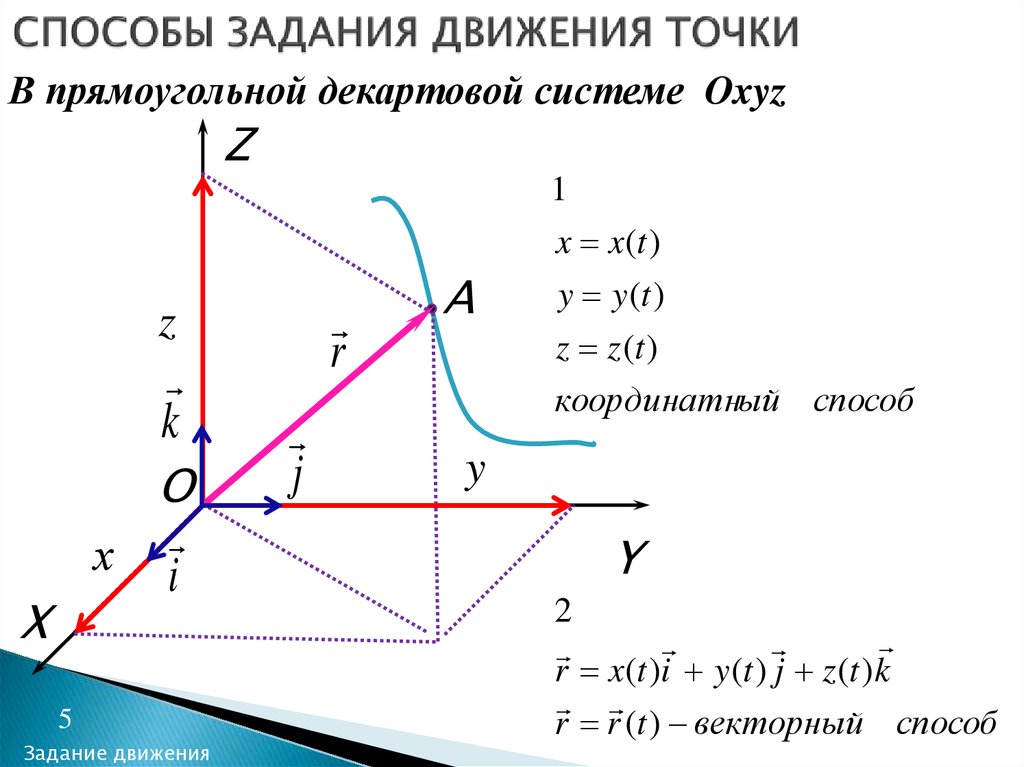
5. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
В прямоугольной декартовой системе OxyzZ
1
r
z
k
O
х i
X
5
Задание движения
j
A
x x(t )
y y (t )
z z (t )
координатный способ
y
Y
2
r x(t )i y (t ) j z (t )k
r r (t ) векторный способ
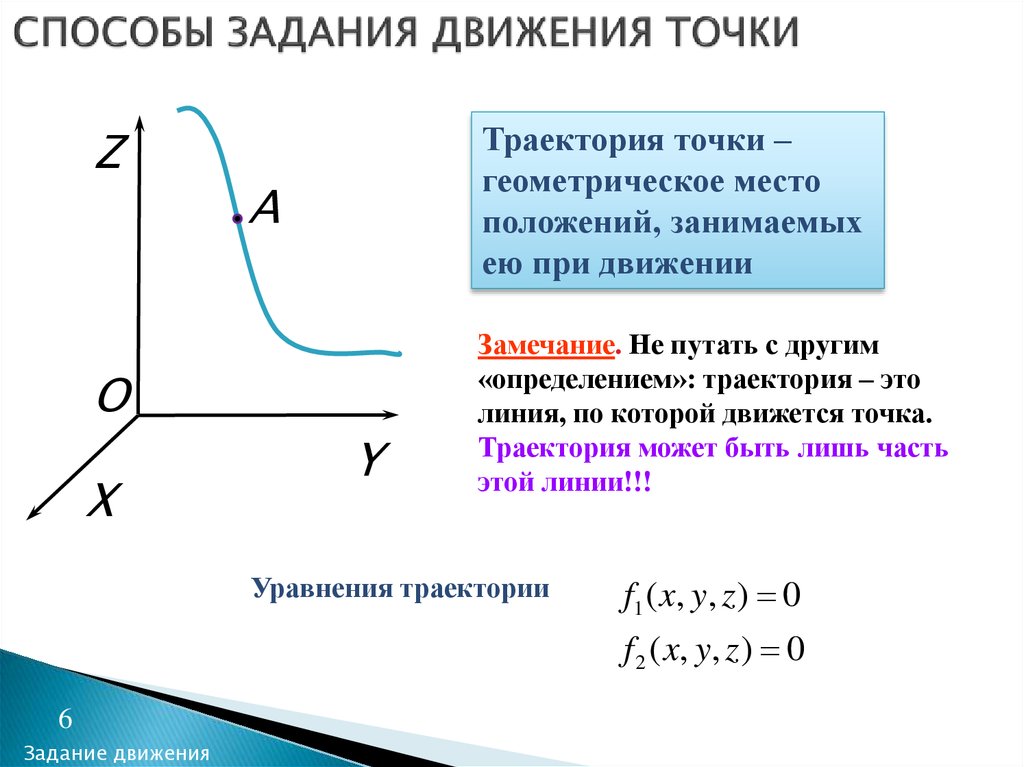
6. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
ZТраектория точки –
геометрическое место
положений, занимаемых
ею при движении
A
O
X
Y
Замечание. Не путать с другим
«определением»: траектория – это
линия, по которой движется точка.
Траектория может быть лишь часть
этой линии!!!
Уравнения траектории
f1 ( x, y, z ) 0
f 2 ( x, y, z ) 0
6
Задание движения
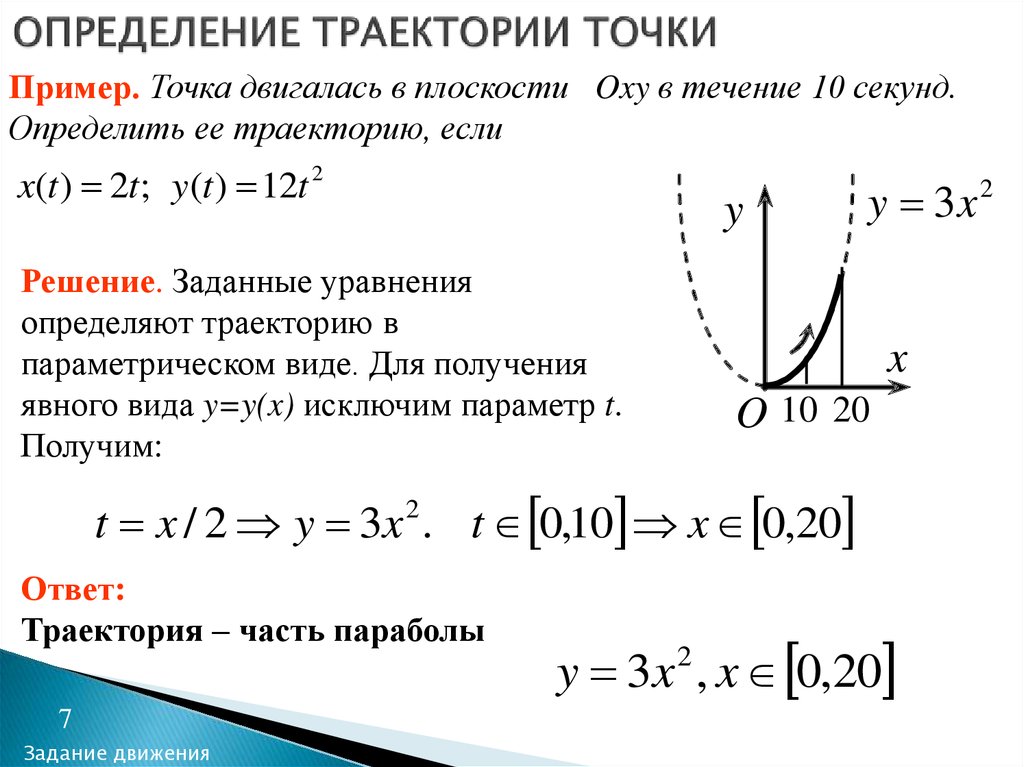
7. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИИ ТОЧКИ
Пример. Точка двигалась в плоскости Oxy в течение 10 секунд.Определить ее траекторию, если
x(t ) 2t; y(t ) 12t 2
y
Решение. Заданные уравнения
определяют траекторию в
параметрическом виде. Для получения
явного вида y=y(x) исключим параметр t.
Получим:
y 3x
x
O 10 20
t x / 2 y 3x . t 0,10 x 0,20
2
Ответ:
Траектория – часть параболы
7
Задание движения
y 3x , x 0,20
2
2
8. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
В естественной системеA
– O+
s
M
B
Пусть линия AB, по которой движется
точка, известна. Тогда положение точки
М на линии можно определить введя
естественную координату s.
s OM ; s s(t )
Такой способ задания движения называется естественным.
1.
2.
3.
4.
8
Задание движения
Уравнения траектории
Начало отсчета
Положительное направление
Закон движения s(t)
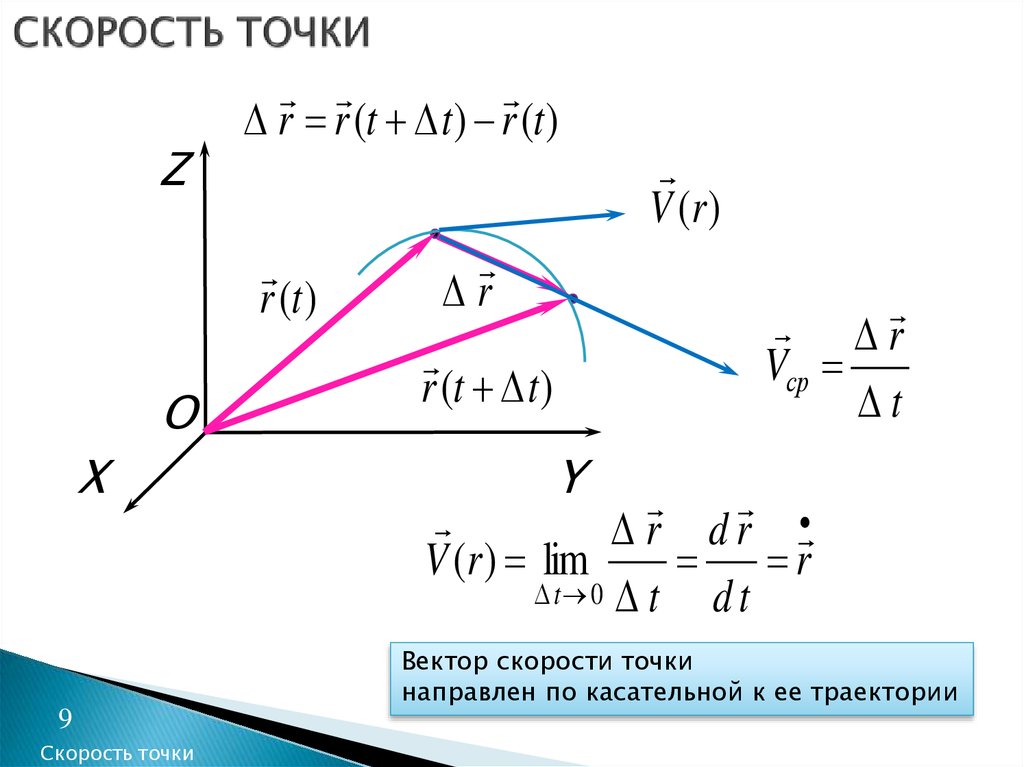
9. СКОРОСТЬ ТОЧКИ
Zr r (t t ) r (t )
r (t )
O
X
r
V (r )
r
Vср
t
r (t t )
Y
r dr
V (r ) lim
r
t 0 t
dt
Вектор скорости точки
направлен по касательной к ее траектории
9
Скорость точки
10. СКОРОСТЬ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ЕЕ ДВИЖЕНИЯ
dx dy dzdr
d
j
k
V (t )
i x jy kz i
dt
dt
dt
dt
dt
V x x
V y y
V z z
10
Скорость точки
V (t ) i vx j vy kvz
V
2
Vx
2
Vy
2
Vz
2
2
2
x y z
11. СКОРОСТЬ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ. ПРИМЕР
Движение точки задано уравнениемt
t
r 2 cos i 2 sin j
6
6
Определить уравнение траектории и скорость точки при t = 1c.
t
x(t ) 2 cos ,
6
t
y(t ) 2 sin
6
2
2
t
t
x
y
сos2 sin 2
1
4
6
6 4
x2 y2
1
4
4
11
Скорость точки
уравнение траектории
(окружность)
12. СКОРОСТЬ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ. ПРИМЕР
Движение точки задано уравнениемt
t
r 2 cos i 2 sin j
6
6
Определить уравнение траектории и скорость точки при t = 1c.
t
Vx x sin ,
3 6
Vx (1) 0,52 м / с
t
Vy y cos
3
6
Vy (1) 0,91м / с
y
V
2
Vx
2
Vy
V
1,1м / с
1
12
Скорость точки
2
x
13. СКОРОСТЬ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ЕЕ ДВИЖЕНИЯ
dr dr ds dsV
s
dt ds dt dt
dr
ds
r
ds
V (t )
dt
Вектор скорости точки направлен по касательной к ее траектории
13
Скорость точки
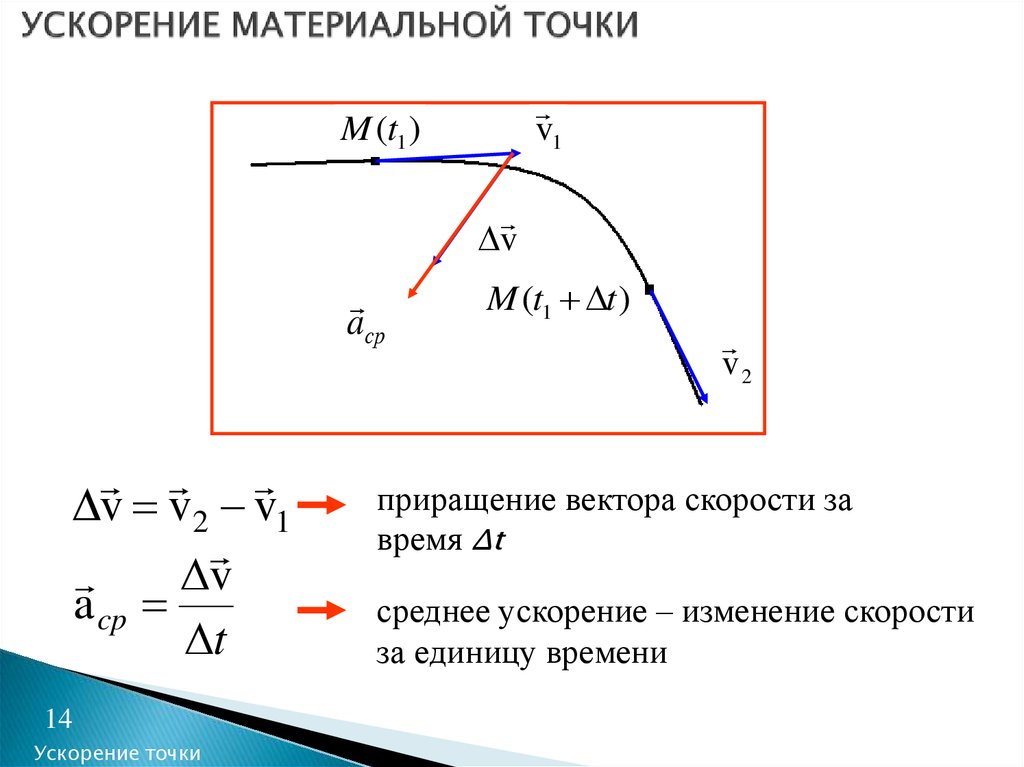
14. УСКОРЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
v1M (t1 )
v
aср
v v2 v1
v
a cp14
t
14
Ускорение точки
M (t1 t )
v2
приращение вектора скорости за
время Δt
среднее ускорение – изменение скорости
за единицу времени
15. УСКОРЕНИЕ ТОЧКИ ПРИ ВЕКТОРНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
a cpv
t
v
d v d 2r
a lim
2
t
dt
dt
t 0
ускорение в данный момент
времени t
Ускорение точки — это векторная величина,
характеризующая быстроту изменения ее скорости и равная
первой производной от скорости или второй производной
от радиус-вектора по времени
15
Ускорение точки
16. УСКОРЕНИЕ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
в декартовой системе координатвектор скорости
v
вектор ускорения
a
vx i v y j vzk
a x i a y j a zk
d v
v x i v y j v z k
a x i a y j a zk
dt
a x v x x
a y v y y
a z v z z
a | a | a 2x a 2y a 2z
16
Ускорение точки
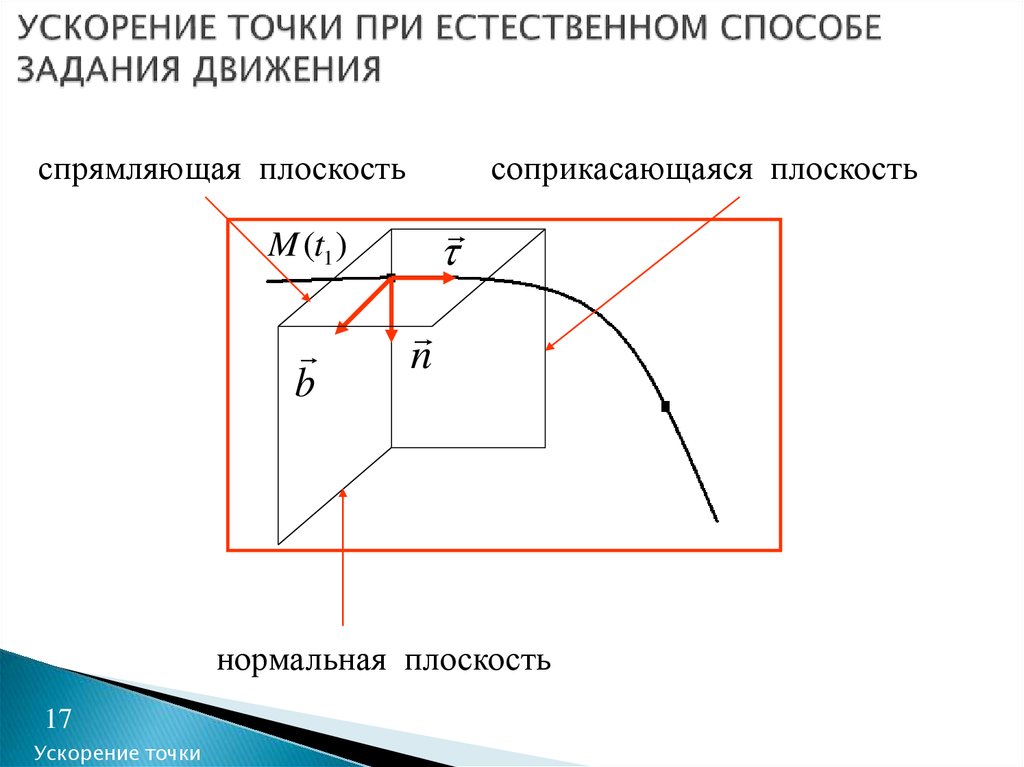
17. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
спрямляющая плоскостьсоприкасающаяся плоскость
M (t1 )
b
n
нормальная плоскость
17
Ускорение точки
18. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
dv dd
a
s s s
dt dt
dt
d
v
dt
Момент времени
d
dt
t
1
c
2
Момент времени
18
Ускорение точки
t+∆t
t
d d
n
dt
dt
2 1
19. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
dlim
t 0 t
dt
При малых ∆φ
d
a s s
dt
1
sin / 2 / 2
d
2 sin / 2
lim
t 0
t
dt
2
lim
t 0 t
a s s n a ann a an
Касательное ускорение
19
Ускорение точки
Нормальное ускорение
20. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
Mds
d
2
2
d
d ds
d
s
v
s
s
s 2
dt
ds
ds dt
угловая скорость вектора
Радиус кривизны
траектории
d 1
ds
ds d
Ускорение точки
s
v
2
2
a a an v n
20
v
an
a
2
a an
2
v2
2
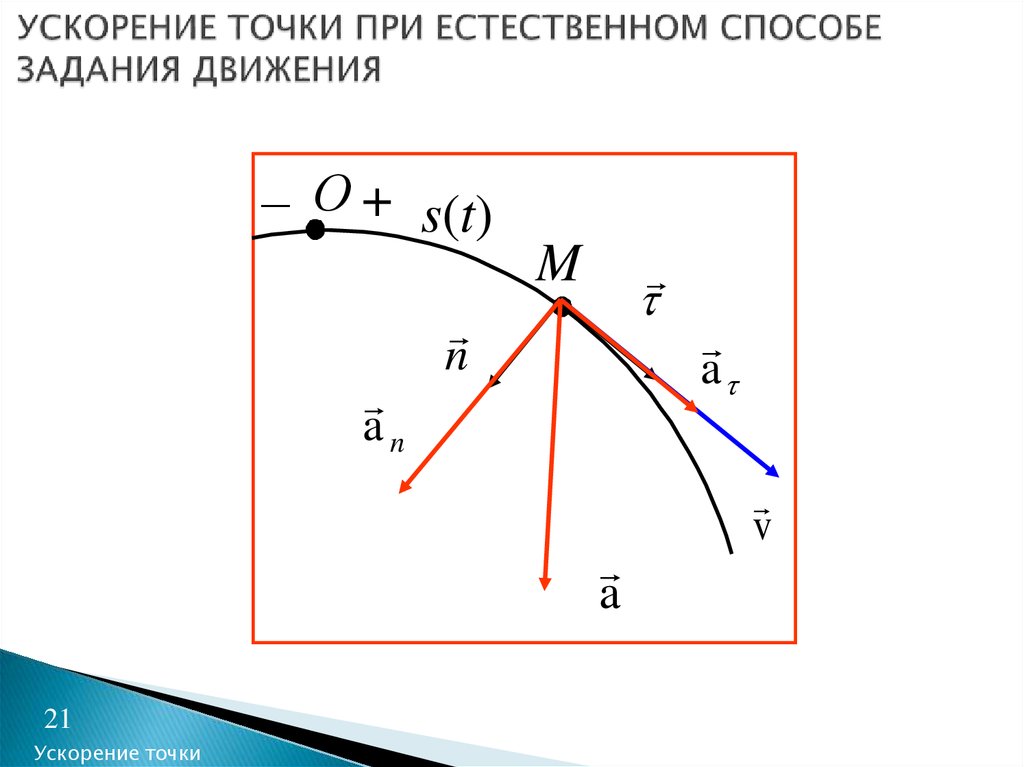
21. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
– О + s(t)M
an
n
a
21
Ускорение точки
a
v
22. ПРОЕКЦИИ СКОРОСТИ И УСКОРЕНИЯ НА ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА
bn
v v vn n vbb
v s
vn 0
22
Ускорение точки
vb 0
a a an n abb
a s a s 2
n
ab 0
23. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТОЧКИ
a 0v const
v t1
v t1 v t2 v t3
v t 2
v t3
Такое движение называется равномерным
Равнопеременное движение
a const
Ускоренное движения:
v a 0
Замедленное движения:
v a 0
v 0
a 0
a 0
23
Ускорение точки
v 0
















 Физика
Физика








