Золотое сечение вокруг нас

1.

"Золотое сечение вокруг
нас"
Автор: Щитов А.К., ученик 9 В класса МБОУ ООШ № 53 г. Бикина
Руководитель проекта: Грязнова Ирина Алексеевна
Исследование математической природы и применения золотого
сечения.

2.

Цел и и задачи
Цель проекта — исследовать суть Золотого сечения, его математическую природу и роль в создании гармоничных объектов.
Для этого я поставлю следующие задачи:
1. Изучить историю открытия и применения Золотого сечения.
2. Разобрать его математическую формулу и способы построения.
3. Найти примеры Золотого сечения в искусстве, архитектуре и живой природе.
4. Провести эксперименты: измерить пропорции в окружающих объектах и сравнить их с идеальным соотношением.

3.

Великие ученые о золотом сечении
Леонардо Фибоначчи (XIII в.)
Цитата Кеплера
«Геометрия владеет двумя сокровищами — теоремой Пифагора и золотым сечением...»

4.

Что такое золотое сечение?
Математическое соотношение
Золотое сечение, также известное как «золотая пропорция», представляет собой
уникальное математическое соотношение, которое на протяжении веков привлекает
внимание ученых, художников и архитекторов. Это соотношение, обозначаемое греческой
буквой φ (фи), приблизительно равно 1.618.
φ = (1 + √5) / 2 ≈ 1.618
Золотое сечение можно построить с помощью циркуля и линейки. Деление отрезка: (a +
b)/a = a/b = φ
Пример
Последовательность Фибоначчи: соотношение соседних чисел стремится к φ
0, 1, 1, 2, 3, 5, 8...чем больше числа в последовательности, тем ближе их отношение к значению φ. На основе чисел Фибоначчи
строится «золотая спираль».

5.

История открытия
1
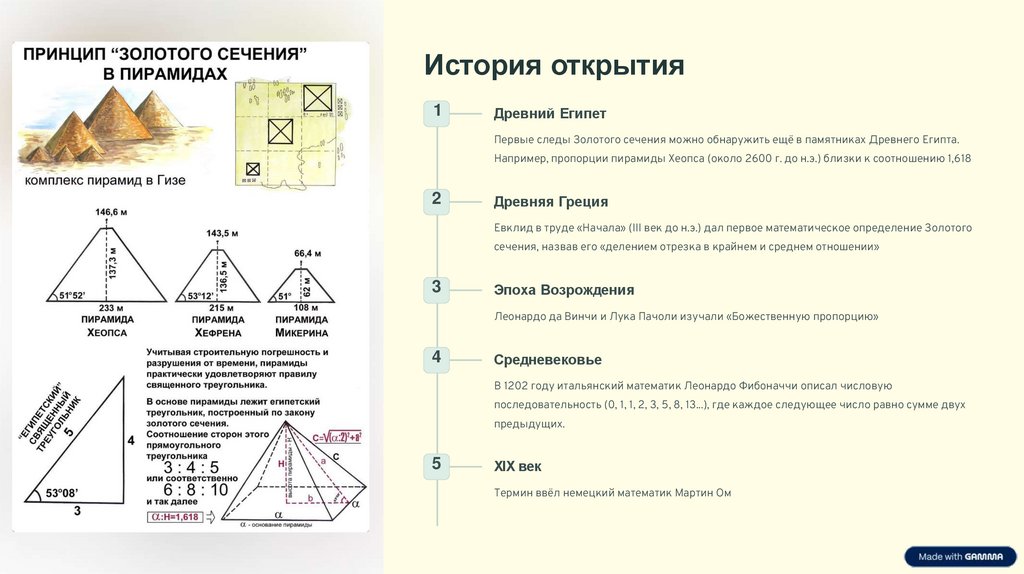
Древний Египет
Первые следы Золотого сечения можно обнаружить ещё в памятниках Древнего Египта.
Например, пропорции пирамиды Хеопса (около 2600 г. до н.э.) близки к соотношению 1,618
2
Древняя Греция
Евклид в труде «Начала» (III век до н.э.) дал первое математическое определение Золотого
сечения, назвав его «делением отрезка в крайнем и среднем отношении»
3
Эпоха Возрождения
Леонардо да Винчи и Лука Пачоли изучали «Божественную пропорцию»
4
Средневековье
В 1202 году итальянский математик Леонардо Фибоначчи описал числовую
последовательность (0, 1, 1, 2, 3, 5, 8, 13...), где каждое следующее число равно сумме двух
предыдущих.
5
XIX век
Термин ввёл немецкий математик Мартин Ом

6.

Золотое сечение в архитектуре
Парфенон в Греции
Московский Кремль
Высота и ширина в пропорции φ
Башни имеют пропорции, близкие к φ
Современный дизайн
Логотипы Apple, Pepsi и дизайн кредитных карт

7.

Золотое сечение в искусстве
Художники Возрождения сознательно изучали Золотое сечение, чтобы достичь идеальной гармонии в своих работах
Леонардо да Винчи
Сандро Боттичелли
Фотография
«Мона Лиза» и «Витрувианский человек»
«Рождение Венеры»
Композиция по правилу φ воспринимается
гармоничнее

8.

Золотое сечение в природе
Растения
Животные
Человек
Отношение высоты
пупка к общему росту
человека составляет
1.618. Длина руки (от
плеча до кончиков
пальцев) делится
Филлотаксис - правило
Форма раковины
локтем в пропорции φ,
расположения листьев
наутилуса и рога
плечо до локтя:
на стебле, листья растут
антилоп, Форма
предплечье с кистью
по спирали
раковины —
=1.618.
логарифмическая
спираль, которая
сохраняет пропорции
при росте.

9.

Практический
эксперимент
1
3
Цел ь
2
Резул ьтат
Проверить восприятие
70% выбрали снимки с
гармонии в фотографиях
композицией по φ
В ы вод
Золотое сечение ассоциируется с красотой подсознательно

10.

Закл ючение
Закл ючение
В ходе выполнения научного проекта, посвященного исследованию золотого сечения, была достигнута основная цель —
глубокое изучение свойств и применения золотого сечения в различных областях знаний. Этот проект позволил не только
раскрыть математические закономерности, связанные с золотым сечением, но и продемонстрировать его значимость в
современном мире.
В процессе работы над проектом были выполнены следующие задачи. Во-первых, была проведена детальная
историческая справка о золотом сечении, начиная с его открытия в античные времена и заканчивая современными
исследованиями. Мы рассмотрели, как это понятие развивалось на протяжении веков, и как оно стало неотъемлемой
частью различных дисциплин, включая математику, искусство, архитектуру и природу. Во-вторых, мы исследовали
применение золотого сечения в различных областях, таких как архитектура, дизайн, живопись и даже в биологии. Это
позволило нам увидеть, как золотое сечение проявляется в окружающем нас мире и как оно используется для создания
гармонии и эстетики.