Похожие презентации:
Математика. Глава V. Дифференциальные уравнения
1.
МатематикаГлава V.
Дифференциальные
уравнения
Преподаватель – доцент, к.п.н.
Ефремова Оксана Николаевна
2.
§ 1. Основные понятияДифференциальные уравнения – уравнения, связывающие
независимые переменные, неизвестную функцию от этих
переменных и её производные или дифференциалы.
Решением дифференциального уравнения называется
функция, которая при подстановке в уравнение обращает его
в тождество.
Если неизвестная функция зависит от одной переменной, то
дифференциальное уравнение называют обыкновенным,
если от нескольких переменных, то в частных производных.
Наивысший
порядок
производной,
входящей
в
дифференциальное уравнение, называется порядком этого
уравнения.
3.
y 3 y 2 y 0обыкновенное дифференциальное
уравнение третьего порядка
y z x x z y
дифференциальное уравнение в
частных производных первого
порядка
x y y xe y 0 обыкновенное дифференциальное
уравнение первого порядка
Процесс отыскания решения дифференциального
уравнения называется его интегрированием, а
график его решения – интегральной кривой.
Общий вид обыкновенного дифференциального
уравнения:
F ( x, y, yʹ, yʺ, …, y(n)) = 0,
4.
§ 2. Дифференциальные уравненияпервого порядка
Общий вид дифференциального уравнения первого
порядка:
F ( x, y, y' ) = 0
x – независимая переменная,
y(x) – искомая функция,
F – заданная функция трех переменных.
y' = f (x, y)
уравнение, разрешённое
относительно производной.
y
x y y xe 0
x 2 y 5xy y 2
y 2 5 xy
y
x2
5.
Дифференциальное уравнение 1-го порядка, разрешенноеотносительно y , имеет две формы записи:
1) обычную, то есть y = f(x, y),
2) дифференциальную, то есть
P(x , y)dx + Q(x , y)dy = 0.
dy
f ( x, y )
1. y f ( x, y )
dx
dy f ( x, y)dx 0, то есть P( x, y ) f ( x, y ), Q( x, y) 1
2. P( x, y)dx Q( x, y)dy 0 Q( x, y)dy P( x, y)dx
P( x, y )
dy
P ( x, y )
, то есть f ( x, y )
Q ( x, y )
dx
Q ( x, y )
Замечание. Если уравнение записано в дифференциальной
форме, то обычно предполагают, что переменные x и y
равноправны.
6.
y 2 xy ?
y x2
y x 5
2
y x2 C
Интегрирование дифференциального уравнения в
общем случае приводит к бесконечному множеству
решений.
Задача Коши. Найти решение дифференциального
уравнения первого порядка, удовлетворяющее
начальному условию.
y' = f (x, y), y( x0 ) y0
начальное условие
y
y ,
x
y ( 4) 1
– задача Коши
7.
Задача Коши. Найти решение дифференциальногоуравнения первого порядка, удовлетворяющее начальному
условию:
y' = f (x, y), y( x0 ) y0
Геометрически, задание начального условия означает, что
на плоскости xOy задается точка (x0,y0), через которую
проходит интегральная кривая y(x).
Теорема (существования и единственности решения задачи
Коши).
Пусть для уравнения y = f(x, y) выполняются два условия:
1) f(x,y) непрерывна в некоторой области D плоскости xOy,
2) fy (x, y) в области D ограничена.
Тогда для любой точки (x0, y0) D существует единственное
решение y = (x) этого уравнения, удовлетворяющее условию
y(x0) = y0.
8.
Общим решением дифференциального уравнения y = f(x, y) вобласти D существования и единственности решения
задачи Коши называется функция
y = (x, C),
зависящая от x и одной произвольной постоянной C, которая удовлетворяет следующим двум условиям:
1) при любом допустимом значении постоянной С она
является решением данного уравнения;
2) каково бы ни было начальное условие y(x0) = y0 (где
(x0, y0) D), можно найти единственное значение C = C0
такое, что функция y = (x , C0) удовлетворяет данному
начальному условию.
Уравнение Φ(x, y, C) = 0, задающее общее решение в неявном
виде, называется общим интегралом уравнения.
Любое решение (интеграл), получающееся из общего решения
(интеграла) при конкретном значении постоянной C (включая C = ), является частным.
9.
Общее решение дифференциального уравненияпервого порядка:
y ( x, C )
x y ln | y | C
функция y задана неявно.
Общий интеграл дифференциального уравнения
первого порядка:
( x , y , C ) 0
y 2 x
y x 2 C – общее решение
x 2 y C 0 – общий интеграл
y x2
2
y x 5
C 0
C 5
- частные решения
10.
Общее решение не всегда описывает все множестворешений дифференциального уравнения.
Интегрируя дифференциальное уравнения, необходимо всегда
проверять, не были ли потеряны в процессе преобразования
какие-либо решения.
Решение y = (x), в каждой точке которого нарушено условие
единственности (т.е. через каждую точку кривой y = (x)
проходит еще хотя бы одна, отличная от y = (x),
интегральная кривая), называется особым.
Особое решение не входит в общее решение дифференциального уравнения, оно всегда «теряется» в процессе интегрирования.
11.
§ 3. Методы интегрированиядифференциальных уравнений
первого порядка
1. Уравнения с разделяющимися
переменными
Определение. Дифференциальное уравнение I-го порядка
называется уравнением с разделяющимися переменными,
если оно имеет вид:
Частный случай. Дифференциальное уравнение I-го порядка с
разделенными переменными имеет вид:
12.
13.
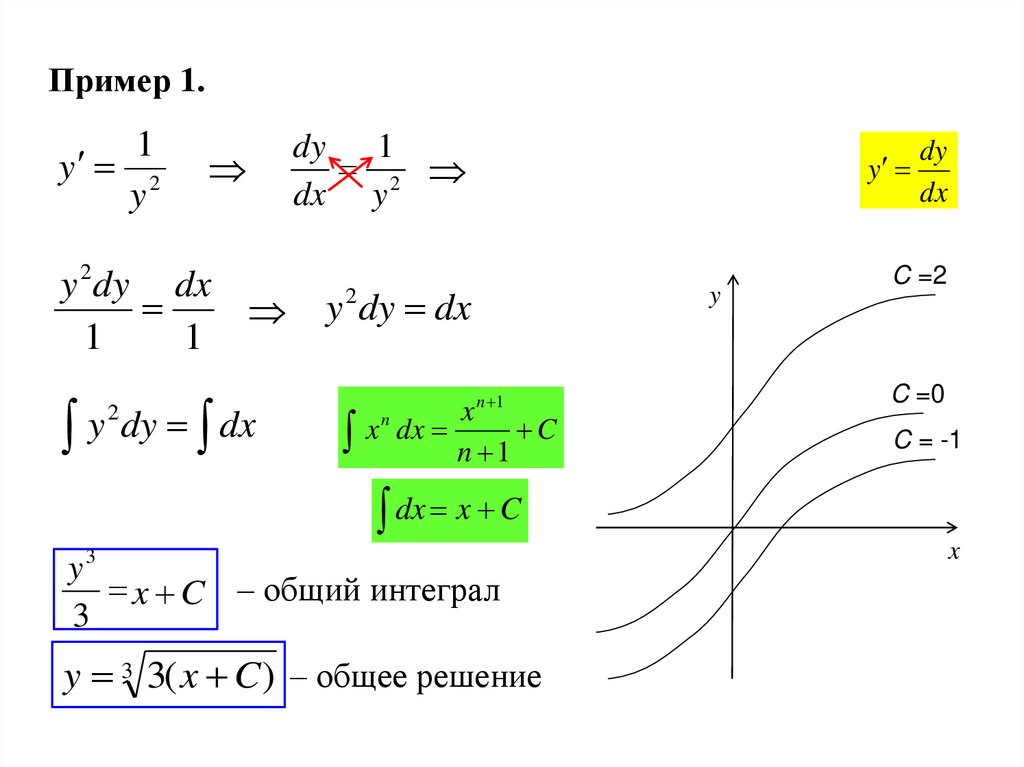
Пример 1.1
y 2
y
dy 1
2
dx y
y 2 dy dx
1
1
y dy dx
y dy dx
x n 1
n
x dx n 1 C
2
2
y
y
dy
dx
C =2
C =0
C = -1
dx x C
y3
x C – общий интеграл
3
y 3 3( x C ) – общее решение
x
14.
Пример 2.y
y ,
x
y ( 4) 1
y
dy
dx
dx
x ln | x | C
dy
dx
dy
y
dy
dx
x
y
y
x
dx
x
ln a ln b ln( a b)
ln | y | ln | x | ln C
b
1
b
ln
a
ln(
a
)
ln | x | ( 1) ln | x | ln(| x | ) ln
|x|
C
1
C
ln | y | ln ln C ln
– общее решение
y
|x|
|x|
x
C
4
C 4
1
– частное решение
y
4
x
1
15.
Пример 3.( y xy)dx ( x xy)dy 0 дифференциальная форма
y (1 x )dx x(1 y )dy 0
записи уравнения
dx
x ln | x | C
y (1 x )dx x(1 y )dy
dx x C
Разделим уравнение на xy:
(1 x )dx
(1 y )dy
x
y
(1 x )dx
(1 y )dy
x y
1 x
1 y
( x x )dx ( y y )dy
ln | x | x ln | y | y C
dx
dy
x dx y dy
– общий интеграл
16.
( y xy)dx ( x xy)dy 017.
18.
2. Однородные уравненияФункция M(x , y) называется однородной степени m (или измерения m), если t 0 справедливо равенство
M(tx , ty) = tm M(x , y).
Подставляем в функцию М(x, y):
x tx
y ty
Примеры однородных функций:
f ( x, y ) x 3 3 x 2 y ,
x2 y2
f ( x, y )
,
xy
19.
2. Однородные уравненияОпределение.
порядка
Дифференциальное
уравнение
первого
y = f(x , y)
называется однородным, если функция f(x,y) является
однородной нулевой степени.
y2 x2
Пример. Проверить, является ли уравнение y
2
x
однородным.
Подставим в уравнение вместо выражение x = tx, y = ty:
(ty)2 (tx)2 t 2 y 2 t 2 x 2 t 2 ( y 2 x 2 ) y 2 x 2
y
2
2 2
2 2
(tx)
t x
t x
x2
Если уравнение не изменилось, то это однородное
уравнение.
20.
2. Однородные уравненияОпределение. Дифференциальное уравнение
первого порядка вида
у = f(y/x)
называется однородным дифференциальным
уравнением.
Однородное уравнение приводится к уравнению с
разделяющимися переменными при помощи замены
y
t
x
y tx
y t x t
21.
22.
Пример1.xy y x
Проверяем, однородное ли уравнение.
Подставляем вместо x → tx, вместо y → ty.
23.
3. Линейные уравнения иуравнения Бернулли
Определение. Дифференциальное уравнение I-го порядка
называется линейным, если сама функция и её производная
входят в уравнение в первой степени и не содержат их
произведения, т.е. уравнения вида
Пример.
xy 2 y x 4 0
P(x)
Q(x)
2y
2y
3
3
y
x
0
y
x
x
x
Следовательно, это уравнение является линейным.
24.
Методы решения линейных дифференциальныхуравнений I-го порядка
1. Метод вариации произвольной постоянной
2. Метод подстановки
25.
Определение. Уравнением Бернулли называетсядифференциальное уравнение вида
где n 0, n 1.
При n = 0 получим линейное уравнение первого порядка.
При n = 1 получим уравнение с разделяющимися
переменными (показать).
Пример. xy y 3x
2
y
1
1/ 2
y
y
3
xy
x
Следовательно, уравнение является уравнением Бернулли.
26.
Методы решения уравнения Бернулли1. Метод замены (сведение уравнения к линейному)
Обе части уравнения
разделить на уn
и сделать замену z = y 1- n , z = (1 – n) y .
Получим дифференциальное уравнение I-го порядка
относительно переменной z:
z /(1 – n) + P(x) z = Q(x).
2. Метод подстановки
Решение ищем в виде произведения двух функций
y = u(x) v(x).
27.
Методы решения уравнения Бернулли1. Метод замены (сведение уравнения к линейному)
Обе части уравнения
разделить на уn
и сделать замену z = y 1- n , z = (1 – n) y .
Получим дифференциальное уравнение I-го порядка
относительно переменной z:
z /(1 – n) + P(x) z = Q(x).
xy y 3x 2 y ,
2. Метод подстановки
Решение ищем в виде произведения двух функций
y = u(x) v(x).
28.
xy y 3x 2 y ,29.
Пример 1.xy 2 y x 0
4
линейное уравнение
2y
y p( x ) y f ( x )
x3
x
y uv y u v uv
y
2uv
2v
3
u v uv
x u v u ( v ) x 3
x
x
0
b ln a ln( a b )
dv
2v
dv
dx
2v
ln | v | 2 ln | x |
2
v
0
1)
dx
x
v
x
x
1
v x 2 v 2
x
6
u
du
x
3
x5 u
2 ) u v x 3 2 x
C
x
dx
6
1
x6
y uv y C 2
6
x
x4 C
y
2 – общее решение
6 x
30.
Пример 2. Найти решение задачи Коши для уравненияxy y 3x 2 y , если начальное условие y (1) 0.
1
y y 3xy1 / 2 y p( x ) y f ( x ) y n уравнение Бернулли
x
1
v
y uv
u v uv uv 3x(uv )1/ 2 u v u( v ) 3x(uv )1 / 2
x
x
y u v uv
0
dv dx
dv v
v
ln | v | ln | x | v x
1) v 0
v
x
dx x
x
du
3u1 / 2 x1 / 2
2 ) u v 3x(uv) u x 3xu x
dx 1/2
3/2
du
u
x
1/ 2
1 / 2
1/ 2
3
x
dx
3
C
u
du
3
x
dx
1/ 2
u
1/ 2
3/ 2
1/ 2
x n 1
x dx n 1 C
n
1/ 2 1/ 2
u x3 C
u ( x 3 C )2
31.
Пример 2. Найти решение задачи Коши для уравненияxy y 3x 2 y , если начальное условие y (1) 0.
1
y y 3xy1 / 2
x
v x
u ( x 3 C )2
y p( x ) y f ( x ) y n
уравнение Бернулли
y uv
y x( x 3 C )2 – общее решение
0 1( 13 C )2 0 (1 C )2 0 1 C C 1
y x( x 3 1)2 – частное решение
32. 4. Уравнения в полных дифференциалах
Определение. Уравнение M(x , y)dx + N(x , y)dy = 0называется уравнением в полных дифференциалах,
если его левая часть является полным дифференциалом
некоторой функции u(x , y) , то есть если
M(x , y)dx + N(x , y)dy = du(x , y).
Общий интеграл уравнения в полных дифференциалах имеет
вид
u(x , y) = C.
Задачи:
1) научиться определять, когда выражение
M(x , y)dx + N(x , y)dy
является полным дифференциалом;
2) научиться находить функцию u(x , y), зная ее полный дифференциал.
33.
ТЕОРЕМА 1.Пусть функции M(x , y), N(x , y) определены и непрерывны
в области D xOy и имеют в ней непрерывные частные
производные
M
y
и
N
.
x
Выражение
M(x, y)dx + N(x, y)dy
представляет собой полный дифференциал некоторой
функции u(x, y) во всех точках области D выполняется
условие
M N
.
y
x
Доказательство
34.
3435.
3536.
3637.
3738.
3839.
3940.
1. Необходимость. Пусть M ( x, y)dx N ( x, y)dy du( x, y).Покажем, что
M N
.
y
x
u
u
u
u
dx dy M ( x, y ) , N ( x, y ) .
Т.к. du( x, y)
y
x
x
y
2u
N
2u
M
.
,
Тогда
x y x
y x y
M
N
По условию теоремы
и
y
x
M N
2u
2u
.
y
x
x y y x
– непрерывные
41.
M N.
2. Достаточность. Пусть
y
x
Найдём такую функцию u(x,y), что
M ( x, y)dx N ( x, y)dy du( x, y),
u
то есть для которой u M ( x, y),
N ( x, y).
y
x
u
Сначала найдём такую функцию u(x,y), что
M ( x, y),
x
для этого проинтегрируем это равенство по х:
u( x, y ) M ( x, y )dx ( y).
Найдём такую функцию ( y), что
u
u
M ( x, y )dx ( y )
N ( x, y)
y y
y
M ( x, y )dx ( y ) N ( x, y )
y
42.
M ( x, y)dxy
Следовательно, искомая функция ( y ) будет существовать,
если выражение N ( x, y )
M ( x, y )dx не зависит от х.
y
Убедимся в этом, продифференцировав его по х,
в результате дифференцирования должен получиться ноль.
( y) N ( x, y)
N
2
N ( x, y )
M ( x, y )dx
M ( x, y )dx
x
y
x y x
N
N
2
M
(
x
,
y
)
dx
M ( x, y )dx
x y x
x x y
N M
N
0
M ( x , y )
x y
x y
N
(
x
,
y
)
M
(
x
,
y
)
dx
dy C.
( y)
y
43.
u( x, y ) M ( x, y )dx ( y )M ( x, y )dx N ( x, y )
M ( x, y )dx dy C.
y
44.
§ 4. Дифференциальные уравнениявысших порядков
Общий вид дифференциального уравнения:
F ( x, y, yʹ, yʺ, …, y(n)) = 0,
где x – независимая переменная,
y(x) – искомая функция,
F – заданная функция (n + 2) переменных.
y (n) = f (x, y , yʹ, …, y(n – 1)) уравнение, разрешённое
относительно старшей
производной.
y ln x ln y y 1
x y 3 y y sin( y ) 0
45.
Интегрирование дифференциального уравнения вобщем случае приводит к бесконечному множеству
решений.
Задача Коши. Найти решение дифференциального
уравнения
y (n) = f (x, y , yʹ, …, y(n – 1)),
удовлетворяющее начальным условиям:
y( x0 ) y00 , y ( x0 ) y10 , y ( x0 ) y20 , ..., y ( n 1) ( x0 ) y( n 1)0
начальные условия
xy x( y )2 y 0, y (2) 2, y (2) 1 – задача Коши
46.
Теорема (существования и единственности решения задачиКоши).
Пусть для уравнения
y(n) = f(x, y, y , y , … , y(n–1))
выполняются два условия:
1) функция f(x, y, y , y , … , y(n–1)) непрерывна как функция
(n + 1)-ой переменной x, y , y , y , … , y(n–1) в некоторой
области D (n + 1)-мерного пространства;
2) функция f(x, y, y , y , … , y(n–1)) имеет в этой области D
ограниченные частные производные по переменным
y, y , y , … , y(n–1) .
Тогда для любой точки (x0, y0, y01, y02, … , y0n–1) D
существует, и притом единственное, решение y = (x)
уравнения, определенное в некотором интервале, содержащем точку x0 , и удовлетворяющее начальным условиям
(x0) = y0, (x0) = y01, (x0) = y02, … , (n–1)(x0) = y0n–1.
47.
Замечание. Единственность решения задачи Коши для уравнения n-го порядка (n > 1) НЕ ОЗНАЧАЕТ, что через данную точку M0(x0 ,y0) плоскости xOy проходит одна интегральная кривая y = (x).Кривых через точку M0 проходит бесконечное множество, а
единственность означает, что они различаются набором
значений y (x0), y (x0), …, y(n–1)(x0) .
Общее решение дифференциального уравнения первого
порядка:
y ( x, C )
Общее решение дифференциального уравнения n-го
порядка:
y ( x, C , C ,..., C )
1
2
n
Общий интеграл дифференциального уравнения n-го
порядка:
( x, y, C1 , C2 ,..., Cn ) 0
48.
§ 5. Дифференциальные уравнения,допускающие понижение порядка
1. F ( x, y ( n ) ) 0 Искомая функция: y= y(x)
n-кратное интегрирование
2. F ( x, y ( k ) , y ( k 1) ,..., y ( n ) ) 0
Искомая функция: y= y(x)
Подстановка: y(k) = t(x)
y(k+1) = tʹ(x) … y(n) = t(n – k)(x)
(n)
F
(
y
,
y
,...,
y
) 0 Искомая функция: y= y(x)
3.
Подстановка: y' = p(y)
y p y p p
…
49.
1. F ( x, y ( n ) ) 0Пример 1. Найти общее решение уравнения
y ln x
dy
ln x d ( y ) ln xdx
y ( y )
dx
dx
dx
y ln xdx u ln x du x x ln x x
u dv
dv dx v x
x
x ln x x C1
y x ln x x C1 y x ln xdx xdx C1dx
x2
x 2 dx x 2
C1 x C2
y ln x
2
2 x
2
1
xdx
2
x2
x2 x2
y ln x
C1x C2
2
4
2
dx
x 2
x
v
2
u ln x du
dv xdx
UdV UV VdU
– общее решение
50.
2. F ( x, y ( k ) , y ( k 1) ,..., y ( n ) ) 0y
Пример 2. Найти общее решение уравнения y x
x
Подстановка y'= t(x) y t
t
t
t
x – линейное относительно t t uv,
t x
x
x
t u v uv
v
dv v
dv dx
uv
v
ln v ln x
u v uv
x
x
dx x
v
x
x
u v x
v x
du
1 du dx u x C1
u x x
dx
2
y
x
(
x
C
)
dy
(
x
t uv x( x C1)
xC1)dx
1
x3 x 2
y
C1 C2 – общее решение
3
2
51.
3. F ( y, y ,..., y ( n ) ) 0Пример 3. Найти общее решение уравнения yy yy ln y ( y )2
Подстановка
y' = p(y)
yp p yp ln y ( p)2
y p ( y ) y p ( y ) p
yp y ln y p
p 0
y 0
y C
p
yp p y ln y p ln y – линейное относительно p p uv, p u v uv
y
dv v
v
v
ln v ln y v y
uv
y
u v uv
ln y
dy y
y
u v ln y
du ln y
1 2
ln ydy
u
ln y C1
du
u ln yd (ln y )
u y ln y dy
y
2
y
dy
1
p uv y ln 2 y C1 2 y ln 2 y 2C1
dx
2
p y
2d ln y
2
ln y
dx
arctg
x C2 – общий интеграл
y ln 2 y 2C 1
1
2C1
2C1
y
52.
§ 6. Линейные дифференциальныеуравнения высших порядков
Линейным дифференциальным уравнением n-го порядка
называется
уравнение,
линейное
относительно
неизвестной функции y и ее производных y , y , … , y(n),
то есть уравнение вида:
p0(x) y(n) + p1(x) y(n – 1) + … + pn – 1(x) y + pn(x) y = g(x),
где pi(x) (i = 0, 1, 2, …, n) и g(x) – заданные функции.
Если g(x) ≡ 0, то уравнение называется линейным
однородным.
Если g(x) ≢ 0, то уравнение называется линейным
неоднородным (или уравнением с правой частью).
53.
Так как p0(x) ≢ 0 , то уравнение можно записать в виде:y(n) + a1(x) y(n – 1) + … + an – 1(x) y + an(x) y = f(x) .
Такое уравнение называют приведённым.
В дальнейшем будем работать только с приведённым
уравнением.
54. 1. Линейные однородные дифференциальные уравнения n-го порядка
y(n) + a1(x) y(n – 1) + … + an – 1(x) y + an(x) y = 0Теорема (свойство решений линейного однородного
дифференциального уравнения).
Если y1(x) и y2(x) являются решениями линейного
однородного дифференциального уравнения, то
y1(x) + y2(x) и C y1(x) ( C ℝ)
тоже является решениями этого уравнения.
Доказательство
1. Покажем, что у1 + у2 является решением:
( y1 y2 )( n ) a1 ( x ) ( y1 y2 )( n 1) an 1 ( x ) ( y1 y2 ) an ( x ) ( y1 y2 )
[ y1( n ) a1 y1( n 1) an 1 y1 an y1 ] [ y2( n ) a1 y2( n 1) an 1 y2 an y2 ]
0 0 0
55.
2. Покажем, что С ∙ у1 является решением:(C y1 )( n ) a1 ( x ) (C y1 ) ( n 1) an 1 ( x ) (C y1 ) an ( x ) (C y1 )
C [ y1( n ) a1 y1( n 1) an 1 y1 an y1 ] C 0 0
Следствие. Если y1, y2, … , yn – решения линейного однородного
дифференциального уравнения, то их линейная комбинация
C1 y1 + C2 y2 + … + Cn yn
тоже является решением этого уравнения для любых
постоянных C1 , C2 , … , Cn .
y(n) + a1(x) y(n – 1) + … + an – 1(x) y + an(x) y = 0
C1 y1 + C2 y2 + … + Cn yn выражение, содержащее n
констант и являющееся решением.
Вопрос: будет ли это выражение являться общим решением?
56.
Пусть y1(x) , y2(x) , … , yn(x) – (n – 1) раз дифференцируемые на[a; b] функции. Запишем для них определитель порядка n вида
W
y1
y1
y1
y2
y2
y2
y3
y3
y3
y1( n 1) y2( n 1) y3( n 1)
yn
yn
yn
yn( n 1)
Определитель W – функция, определенная на [a; b].
Его обозначают W(x) или W[y1, y2, … , yn ] и называют определителем Вронского (вронскианом) функций y1, y2, … , yn.
57.
Теорема (необходимое условие линейной зависимостифункций). Если функции y1(x), y2(x , … , yn(x) (n – 1) раз
дифференцируемы и линейно зависимы на [a; b], то их определитель Вронского на [a; b] тождественно равен нулю.
Теорема (достаточное условие линейной независимости
решений линейного однородного дифференциального
уравнения n-го порядка).
Если n решений линейно независимы на [a; b], то их
определитель Вронского W[y1, y2, … , yn ] не может
обратиться в нуль ни в одной точке этого промежутка.
58.
Вывод:1) если W[y1 , y2 , … , yn ] ≡ 0, то решения y1(x) , y2(x) , … , yn(x)
линейно зависимы;
2) если W[y1 , y2 , … , yn ] 0, x [a;b], то решения
y1(x) , y2(x) , … , yn(x) линейно независимы.
Система n линейно независимых решений линейного однородного дифференциального уравнения n-го порядка называется
его фундаментальной системой решений.
Теорема. Если y1, y2, … , yn – фундаментальная система
решений линейного однородного уравнения n-го порядка, то его
общее решение имеет вид:
y C1 y1 C2 y2 Cn yn .
59.
2. Линейные однородныедифференциальные уравнения n-го порядка
с постоянными коэффициентами
y(n) + a1 y(n – 1) + … + an – 1 y + an y = 0,
где a1 , a2 , … , an – некоторые действительные числа.
Решения уравнения будем искать в виде y = eкx,
где к – некоторая постоянная.
Тогда
y = к eк x, y = к2 eк x, y = к3 eк x, … , y(n) = кn eк x.
Подставляя y, y , y , … , y(n) в уравнение, получим:
кn eк x + a1 кn – 1 eк x + … + an – 1 к eк x + an eк x = 0,
кn + a1 кn – 1 + … + an – 1 к + an = 0.
Полученное уравнение называется характеристическим
уравнением дифференциального уравнения, а его корни –
характеристическими корнями.
60.
Теорема.Пусть к – характеристический корень. Тогда
1) если к ℝ – корень кратности s, то решениями
дифференциального уравнения являются функции
eк x, x eк x, x2 eк x, …, xs – 1 eк x;
2) если к = a + bi ℂ – корень кратности s, то a – bi тоже
является
корнем
кратности
s,
а
решениями
дифференциального уравнения являются функции
ea x cosbx, xea x cosbx, x2ea x cosbx, …, xs – 1ea x cosbx
ea x sinbx, xea x sinbx, x2ea x sinbx, …, xs – 1ea x sinbx.
Найденные таким образом n решений образуют
фундаментальную систему решений.
61.
y py qy 01. Составляем характеристическое уравнение.
y k 2 , y k , y k0
k 2 pk q 0
y 3 y 2 y 0
k 2 3k 2 0
2. Решаем характеристическое уравнение.
k1 ≠ k2
y1 e k1x ,
y 2 e k2 x
k1 = k2 = k
a ± bi
y1 e kx ,
y2 xe kx
y1 e ax cos bx,
3. Записываем общее решение:
y C1 y1 C2 y2
y2 e ax sin bx
62.
y py qy 0k1 ≠ k2
y1 e k1x ,
y 2 e k2 x
k1 = k2 = k
a ± bi
y1 e kx ,
y2 xe kx
y1 e ax cos bx,
y2 e ax sin bx
Пример 1. Найти общее решение уравнения y 4 y 5 y 0
Составляем характеристическое уравнение:
y k 2 , y k , y k0 k 2 4k 5 0
D 42 4 ( 5) 36
4 36 4 6
k
2
2
y1 e x ,
4 6
k1
1
2
y 2 e 5 x
Общее решение:
y C1e x C2e 5 x
4 6
k2
5
2
y C1 y1 C2 y2
63.
k1 ≠ k2y1 e k1x ,
y 2 e k2 x
k1 = k2 = k
a ± bi
y1 e kx ,
y2 xe kx
y1 e ax cos bx,
y2 e ax sin bx
Пример 2. Найти общее решение уравнения y 4 y 4 y 0
Характеристическое уравнение: k 2 4 k 4 0 (k 2)2 0 k1,2 2
y1 e 2 x
y2 xe 2 x
Общее решение:
y C1e 2 x C2 xe 2 x
Пример 3. Найти общее решение уравнения y 4 y 5 y 0
Характеристическое уравнение: k 2 4 k 5 0 D 42 4 5 4
4 4 4 2 1
a 2, b 1
2 1 2 i
k1,2
2
2
y1 e 2 x cos x,
y2 e 2 x sin x
Общее решение:
y C1e 2 x cos x C2e 2 x sin x
64.
3. Линейные неоднородныедифференциальные уравнения 2-го порядка
с постоянными коэффициентами
Метод вариации произвольной постоянной
y + a1 y + a2 y = f(x), где a1, a2 – некоторые числа.
Рассмотрим соответствующее ему однородное уравнение
y + a1 y + a2 y = 0.
Пусть y1(х), y2(х) – ФСР этого уравнения.
Тогда его общее решение имеет вид:
y0 = C1 y1 + C2 y2 ,
где C1, C2 – произвольные постоянные.
Пусть C1(x), C2(x) – некоторые функции.
Тогда решение неоднородного уравнения имеет вид:
y = C1(x) y1 + C2(x) y2.
65.
Раскроем скобки в полученном решении и сгруппируемслагаемые:
n
n
n
i 1
i 1
i 1
y i ( x ) Ci yi Ci yi i ( x ) yi .
Первая сумма – общее решение однородного уравнения,
вторая сумма – частное решение неоднородного уравнения
(получается из общего решения при Ci = 0).
Теорема (о структуре решения неоднородного уравнения).
Общее решение линейного неоднородного уравнения n–го
порядка равно сумме общего решения соответствующего ему
однородного уравнения и любого частного решения ỹ(x)
неоднородного уравнения, то есть имеет вид
y(x) = C1 y1 + C2 y2 + … + Cn yn + ỹ(x),
где y1 , y2 , … , yn – фундаментальная система решений
соответствующего линейного однородного уравнения.
66.
y(x) = C1 y1 + C2 y2 + … + Cn yn + ỹ(x)Доказательство
1. Покажем, что y(x) является решением линейного неоднородного уравнения
y(n) + a1(x) y(n – 1) + … + an – 1(x) y + an(x) y = f(x) .
~
Ci yi ( x ) y ( x )
i 1
n
n
(n)
( n 1)
~
a 1 ( x ) Ci yi ( x ) y ( x )
i 1
n
~
an ( x ) Ci yi ( x ) y ( x )
i 1
n
Ci yi( n ) ( x ) a1 ( x ) yi( n 1) ( x ) an ( x ) yi ( x )
i 1
0
y ( n ) ( x) a1 ( x) ~
y ( n 1) ( x) an ( x) ~
y ( x)
~
0 f ( x) f ( x)
f(x)
67.
4. Линейные неоднородныедифференциальные уравнения n-го порядка
с постоянными коэффициентами
y(n) + a1 y(n – 1) + … + an – 1 y + an y = f(x)
1. Метод вариации произвольной постоянной
(метод Лагранжа).
2. Метод позволяет найти общее решение в виде
суммы двух решений: общего решения
соответствующего однородного
дифференциального уравнения и частного
решения (которое подбирается по виду
правой части уравнения).
68.
Теорема (о структуре решения неоднородного уравнения).Общее решение линейного неоднородного уравнения n–го
порядка равно сумме общего решения соответствующего ему
однородного уравнения и любого частного решения ỹ(x)
неоднородного уравнения, то есть имеет вид
y(x) = C1 y1 + C2 y2 + … + Cn yn + ỹ(x),
где y1, y2, … , yn – фундаментальная система решений
соответствующего линейного однородного уравнения.
Доказательство
69.
Дано дифференциальное неоднородное уравнение порядкаn с постоянными коэффициентами
y(n) + a1 y(n – 1) + … + an – 1 y + an y = f(x)
Пусть правая часть
f(x) линейного неоднородного
уравнения с постоянными коэффициентами имеет вид:
1) f(x) = ea x Pn(x), или
2) f(x) = ea x [Pn(x) cosbx + Qm(x) sinbx ],
где
Pn(x), Qm(x) – многочлены степени
соответственно, a и b – некоторые числа.
n
и
m
69
70.
Теорема (о структуре частного решения).1. Если правая часть линейного неоднородного уравнения с
постоянными коэффициентами имеет f(x) = ea x Pn(x), то
частным решением уравнения является функция вида
y = xr An (x) ea x,
где An (x) многочлен степени n,
r – кратность характеристического корня a.
2. Если правая часть линейного неоднородного уравнения с
постоянными коэффициентами имеет вид
f(x) = ea x [Pn(x) cosbx + Qm(x) sinbx ],
то частным решением уравнения является функция вида
y = xr ea x [Al(x) cosbx + Bl(x) sinbx ],
где
Al (x) и Bl (x) – многочлены степени l,
l – наибольшая из степеней многочленов Pn(x), Qm(x),
r – кратность характеристического корня a bi.
71.
Замечание. Если число a (a + bi) не является корнемхарактеристического уравнения, то r = 0.
Общий вид многочленов степени 0, 1, 2, 3, ...
Р0(х) = А
Р1(х) = Ах + В
Р2 (х) = Ах2 + Вх + С
Р3 (х) = Ах3 + Вх2 + Сх + D
…
71
72.
Пример 1. Найти решение уравнения у + 2у + у = х + 3.Решение. Решаем соответствующее ЛОДУ: у + 2у + у = 0.
Составляем характеристическое уравнение
к2 + 2к +1 = 0 (к + 1)2 = 0 к1,2 = ( 1) действительный корень кратности 2.
Тогда у1 = е-х, у2 = хе-х.
Получим
у0 = С1 е-х + С2 хе-х общее решение ЛОДУ.
По условию правая часть уравнения имеет вид:
f(x) = x f(x) = x e0 x.
Следовательно, a = 0 к1,2 , т.е. a не корень характеристического уравнения.
Так как Р(х) = х + 3 n = 1 степень многочлена.
Тогда частное решение ЛНДУ будем искать в виде:
у = (Ах + В) e0 x у = (Ах + В).
Продифференцируем дважды у , подставим у и её производные в первоначальное
уравнение и найдем коэффициенты А и В:
у = А, у = 0;
у + 2у + у = х + 3 0 + 2А + (2Ах + В) = х + 3.
Раскроем скобки и приравняем коэффициенты в левой и правой частях уравнений при
одинаковых степенях х:
2Ах + (2А + В) = 1 х + 3 х: 2А = 1 А = ½, х0 : 2А + В = 3 В = 2.
Получим у = (х/2 + 2).
Окончательно, у = у0 + у = С1 е-х + С2 хе-х + (х/2 + 2) общее решение ЛНДУ.
Ответ. у = С1 е-х + С2 хе-х + (х/2 + 2).
72














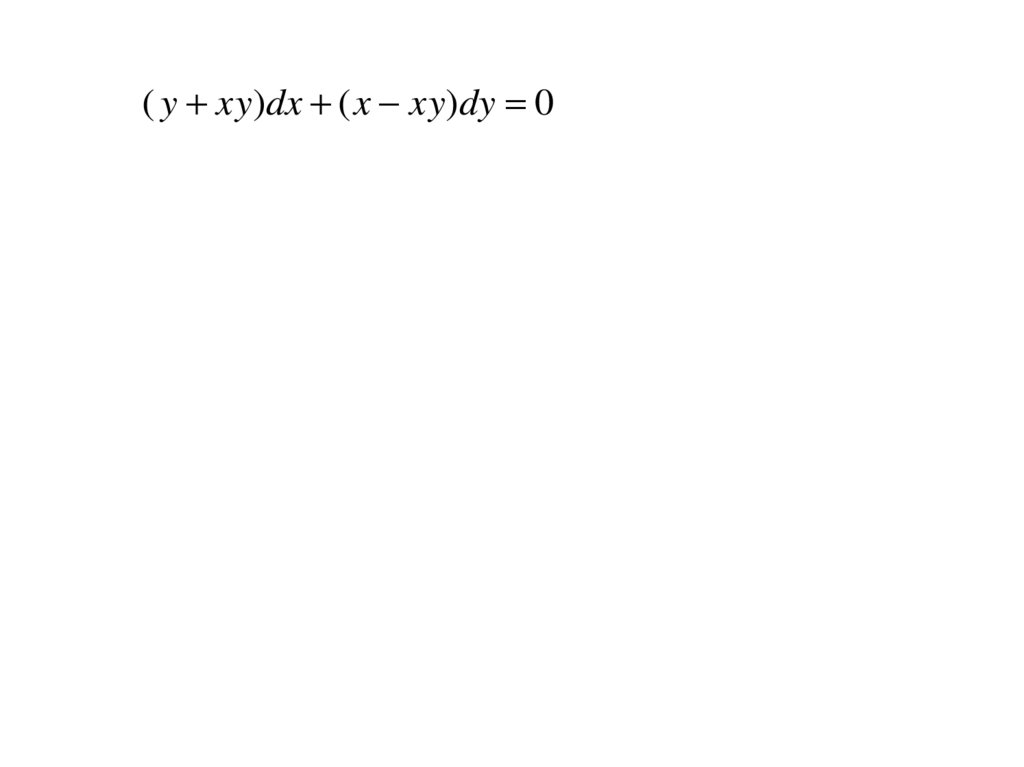











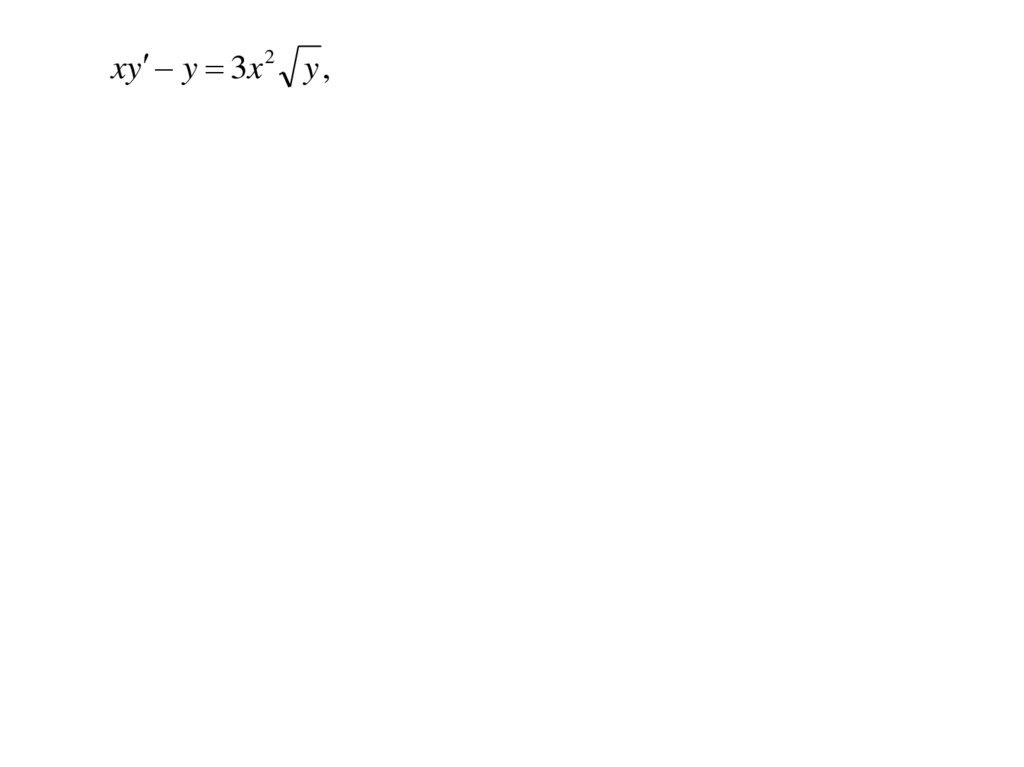














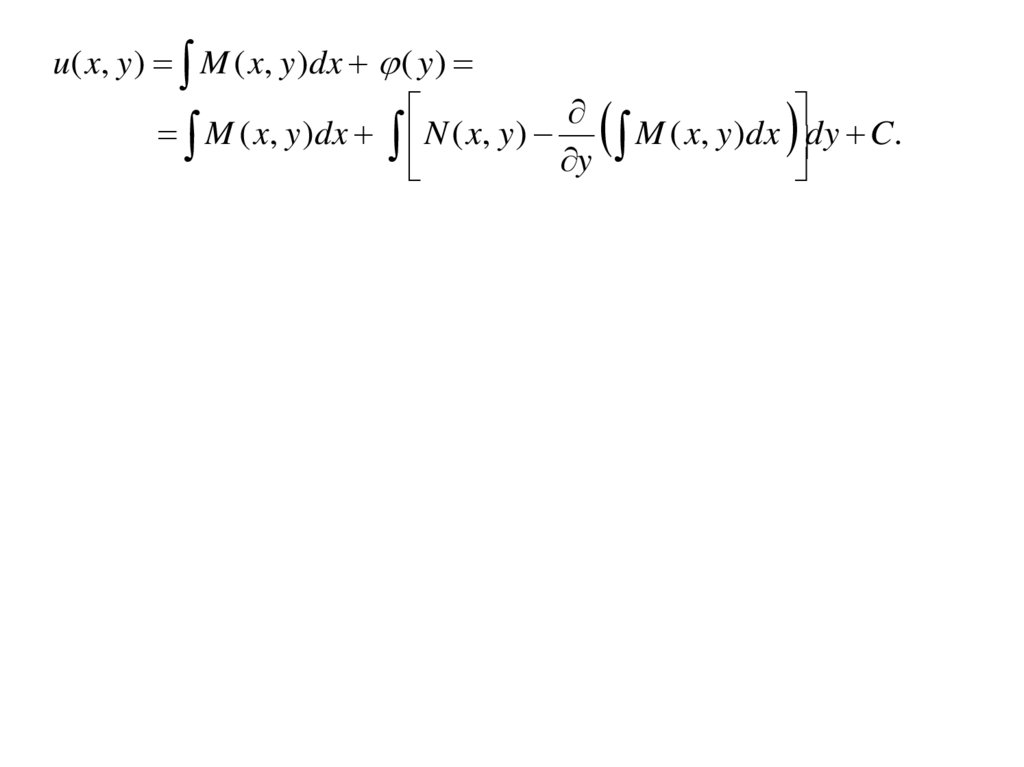































 Математика
Математика








