Похожие презентации:
Дифференциальные уравнения
1.
• Лекция 13.• 2 семестр
2.
12 ln x
y y y
x
x
1. ДУ с разделяющимися
переменными
dy
y
2. Однородные уравнения
dx
x
3. Линейные уравнения
4. Уравнения Бернулли
y P( x ) y = Q( x )
k
y p( x ) y = q( x ) y ,
k Q, k 0, k 1.
5. Уравнения в полных
P ( x; y )dx Q( x; y )dy = 0
дифференциалах
Р у = Q x
3.
1. ДУ с разделяющимисяпеременными
dy
y
2. Однородные уравнения
dx
x
3. Линейные уравнения
4. Уравнения Бернулли
y P( x ) y = Q( x )
k
y p( x ) y = q( x ) y ,
k Q, k 0, k 1.
5. Уравнения в полных
P ( x; y )dx Q( x; y )dy = 0
дифференциалах
Р у = Q x
4.
x y y ln y ln xy y
y ln
x x
1. ДУ с разделяющимися
переменными
dy
y
2. Однородные уравнения
dx
x
3. Линейные уравнения
4. Уравнения Бернулли
y P( x ) y = Q( x )
k
y p( x ) y = q( x ) y ,
k Q, k 0, k 1.
5. Уравнения в полных
P ( x; y )dx Q( x; y )dy = 0
дифференциалах
Р у = Q x
5.
Замечание. ДУ может быть линейным или уравнениемБернулли не только относительно y, но и относительно x.
x P( y ) x = Q( y ).
x P ( y ) x = Q( y ) x k .
Тогда решение уравнения ищется в виде:
x( y) = U ( y)V ( y), x = U V V U .
6.
dy1
dx x cos y sin 2 y
dx
x cos y sin 2 y
dy
1. ДУ с разделяющимися
переменными
dy
y
2. Однородные уравнения
dx
x
3. Линейные уравнения
y P( x ) y = Q( x )
x cos y x k sin
2
y
Q, k 0, k 1.
4. Уравнения Бернулли
k
y p( x ) y = q( x ) y ,
5. Уравнения в полных
P ( x; y )dx Q( x; y )dy = 0
дифференциалах
Р у = Q x
7.
2 y ln y y xx
y
1. ДУ с разделяющимися
переменными
dy
y
2. Однородные уравнения
dx
x
3. Линейные уравнения
y P( x ) y = Q( x )
k
y p( x ) y = q( x ) y ,
x
2 ln y 1k Q, k 0, k 1.
x
5. Уравнения в полных
P ( x; y )dx Q( x; y )dy = 0
y
дифференциалах
4. Уравнения Бернулли
Р у = Q x
8.
РЕШЕНИЕ ЗАДАЧ9.
ПримерРешить ДУ
2y
2
y
5x ;
x
y u v, y u v u v
2
u v u v uv 5 x 2
x
1
dv
2
1
1)
dx ln v 2 ln x ln 2 ; v 2
v
x
x
x
1
2) u 2 5 x 2 u 5 x 4 u x 5 c;
x
1
c
3
y ( x c) 2 x 2
x
x
5
9
10.
ПримерРешить ДУ
y y e y
6x
у u v;
2
- уравнение Бернулли
у u v u v
u v u v uv e (uv)
6x
2
u v u(v v) (uv) e
2 6 x
v v 0;
u v (uv) e ;
2 6 x
dv
x
1) v v 0 dx ln v x v e
v
10
11.
v eu v (uv) e ;
2 6 x
x
e u u e e u u e
2 2 x 6 x
x
u /3 e
3
u e c;
3
3x
3x
2
3x
/ 3 c / 3
1
3
u (e c) ;
3x
y uv e (e c)
x
3x
1
3
5
12.
ПримерРешить ДУ
2
3 xy y xy , y 1 3.
y uv, y u v uv .
3xu v 3xuv 3uv xu 2v 2 , 3xu v 3u xv v xu 2v 2 .
xv v 0, 1) dv dx , ln v ln x , v 1 .
v x
x
2
1
1
2
2
2
u
2) 3xu v xu v , 3xu xu
, 3u
,
2
x
x
x
du
dx
3
3
3
, ln x ln C , u
.
2 x
u
ln Cx
u
3
y
,
x ln Cx
3
y
.
x ln x 1
12
13. Пример
Решить ДУe x y sin y dx e y x x cos y dy 0.
P
Q
1 cos y,
1 cos y.
y
x
u
P x, y ,
x
u e x y sin y dx y e x xy x sin y y .
u
x x cos y y Q x, y x x cos y e y ,
y
y e y , y e y ,
e x xy x sin y e y C.
13
14. Пример
Решить ДУ(3 x 6 xy ) dx (6 x y 4 y ) dy = 0,
2
2
2
3
y(1) = 1
Py ( x; y ) = (3 x 2 6 xy 2 ) y = 12 xy,
Py ( x; y ) = Q x ( x; y )
2
3
Q x ( x; y ) = (6 x y 4 y ) x = 12 xy,
Выполнение критерия означает, что существует некая функция
U ( x; y ) , для которой
U
2
2
P ( x; y ) = 3 x 6 xy = x
Q( x; y ) = 6 x 2 y 4 y 3 = U
y
15.
Из первого равенства, интегрируя по хU1 ( x; y ) = (3 x 6 xy )dx = x 3 x y ,
2
2
3
2
2
Из второго равенства, интегрируя по у
U 2 ( x; y ) = (6 x y 4 y )dy = 3 x y y
2
3
2
2
4
Искомая функция
U ( x; y ) = U1
+(недостающие слагаемые из U 2 ) =
x 3x y y
3
2
2
Общий интеграл уравнения
x 3x y y = c
3
2
2
4
4
16. Пример
2 y22
x
e
dx
x
y
e
t
g
y dy = 0.
Решить ДУ
y2
2
y2
P ( x; y ) = x e , Q( x; y ) = x y e tg 2 y.
Здесь
y2
Проверяем критерий:
Py = 2 xye
y2
y2
Qx = 2 xye .
Частные производные равны. Данное уравнение есть уравнени
в полных дифференциалах. Нужно найти функцию U ( x; y ).
2
2
2
2
x
y
y
y
Из U x = P ( x; y ) = x e находим U1 ( x; y ) = x e dx =
e .
2
2
Из U y = Q( x; y ) = x 2 y e y tg 2 y
находим
2 y2
2
2 1 y2
U 2 ( x; y ) = x y e tg y dy = x e tgy y .
2
вторая функция включает в себя первую, поэтому
x 2 y2
U ( x; y ) =
e tgy y.
2
Общий интеграл уравнения
x 2 y2
e tgy y = C .
2
17.
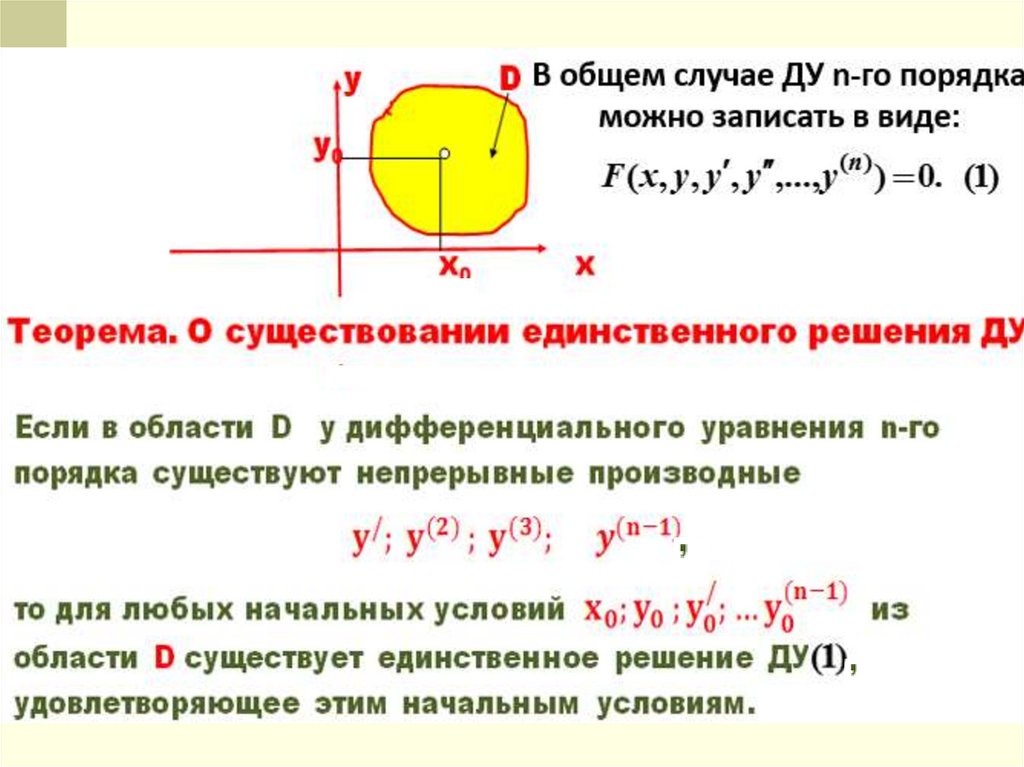
18. Уравнения высших порядков
ДУ 2-го порядка называется уравнение,которое содержит независимую переменную х
искомую функцию у и ее производные 1-го и 2-го порядка.
Уравнение
y = f ( x; y; y ),
2-го порядка может быть записано в явной форме
если оно разрешено относительно старшей производной
или в неявной
F ( x; y; y ; y ) = 0.
Р е ш е н и е м дифференциального уравнения 2-го порядка
называется любая дважды дифференцируемая функция y = y ( x ),
которая при подстановке в уравнение, обращает его в тождество.
19.
О б щ и м р е ш е н и е м уравнения 2-го порядка называетсяфункция
y = y( x; C1; C2 ).
Заметим, что количество констант в общем решении уравнения
равно порядку уравнения.
З а д а ч а К о ш и для уравнения состоит в нахождении
частного решения уравнения, удовлетворяющего заданным
начальным условиям.
y( x0 ) = y0 ,
y ( x0 ) = y0 .
20. УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Тип I. Уравнения видаy ( n) = f ( x ).
Решение находится путем последовательного интегрирования.
y = ( ( (...( f ( x )dx )...)dx )dx )dx .
n раз
Пример. Решить ДУ y = sin x 2 x.
y = y (4) dx = (sin x 2 x ) dx = cos x x 2 C1 .
3
x
y = y dx = ( cos x x 2 C1 ) dx = sin x
C1 x C 2 .
3
3
x
y = y dx = ( sin x
C1 x C 2 ) dx = 4
2
(4)
x
x
cos x
C1
C2 x C3 .
12
2
4
2
x
x
y = y dx = (cos x
C1
C 2 x C 3 ) dx =
12
2 x5
x3
x2
= sin x
C1
C2
C3 x C4
60
6
2
3
общее решение уравнения
21.
Примерy
( 4)
sin 2 x
1
y sin 2 xdx cos 2 x c1
2
1
1
y ( cos 2 x c1 )dx sin 2 x c1 x c2
2
4
2
1
x
y cos 2 x c1 c2 x c3
8
2
3
2
1
x
x
y sin 2 x c1 c2 c3 x c4
16
6
2
22.
Примерy x.
y x 2 0, y x 2 0.
2
x
y
C1,
2
3
x
y
C1x C2 ,
6
3
4
2 C1 0,
8
2C1 C2 0.
6
C1 2, C2 8 / 3.
x
y
2 x 8 / 3.
6
23.
Тип II.F ( x; y ; y ) = 0.
y = z( x ), y = ( y ) x = z ( x )
Пример. Решить ДУ y x ln x y = 0.
После подстановки получаем уравнение первого порядка
z x ln x z = 0.
Разделяем переменные
dz
x ln x = z;
dx
dz
dx
=
,
z
x ln x
ln | z |= ln | ln x | ln C1 ,
dz
dx
,
=
z
x ln x
у z = C1 ln x.
y = y x dx = C1 ln x dx = C1 x(ln x 1) C2 .
23
24.
F ( y; y ; y ) = 0.Тип III.
y x = p( y ),
dp
y xx = p y y x = p y p = p.
dy
y
y y e = 0.
Пример. Решить ДУ
y
p
p
pe
=0
y
y y e = 0
y x = p( y ), y xх = p y p
p ( p e y ) = 0.
1) p = 0, y x = 0, y = const .
dp
2)
= e y dp = e y dy p = e y C1 ,
dy
dy
dy
y
y
y = e C1
= e C1 y
= dx.
dx
e C1
1
1
C1 e y e y dy
y
=
dx
.
y ln C1 e
y
C1
e C1
C1
= x C .
2
24
25.
1Пример.Решить задачу Коши y =
, y(0) = y (0) = 0.
y
1
1
dp
1
y =
p p=
p=
y x = p( y ), y x = p y p
dy
y
y
y
dy
p2
C1
=2 y
p = 4 y C1 .
p dp =
2
2
y
Так как y (0) = p(0) = 0, y(0) = 0,
0 = 4 0 C1
C1 = 0. y = 4 y 0 = 24 y
dy
dy
24 3
4
= 2 y
= dx
y = x C2 .
4
dx
3
2 y
24 3
Так как y(0) = 0, то
0 = 0 C 2 C 2 = 0.
3
4/3
Частное решение
3
y = x .
2
25
26. Комплексные числа
Комплексным числом Z называетсявыражение вида
z i
где и – действительные числа,
а i – мнимая единица.
i 1
2
27.
Два комплексных числаz i ,
z i
называются комплексно сопряженными.
Справедливо равенство
z z
2
2
28. Пример.
4 2x 25 0
1. Вычислить
2. Решить уравнение
3. Решить уравнение
x 2x 5 0
2
Решение. 1.
4
4 i 2i
2
29.
x 25x 25 0
x 25 5i
2
2
2.
3.
x 2x 5 0
2
D ( 2) 4 5 16
2 16 2 4i
x1
1 2i
2
2
2 16
x2
1 2i
2
2
30.
Функции y1(x), y2(x), … , yn(x) линейнонезависимы на I=(a,b), если существуют
действительные числа 1 , 2 , … , n, не все
равные нулю, такие, что для всех x I,
выполняется тождество
1 y1(x) + 2 y2(x) +…+ n yn(x) 0.
Функции y1(x) , y2(x) , … , yn(x) линейно
зависимы, если это тождество выполняется
лишь в случае, когда
1 = 2 =…= n =0.
31.
ТЕОРЕМА.Для того, чтобы функции y1(x) , y2(x) , … , yn(x) –
были линейно независимы на I=(a,b) необходимо и
достаточно, чтобы определитель Вронского
(вронскиан) W(x) был отличен от нуля в каждой
точке x0 I. То есть x0 I
W( y1 , y2 ,..., yn )
y1
y1 ( x0 )
y1 ( x0 )
y2 ( x0 )
y 2 ( x0 )
...
...
yn ( x0 )
y n ( x0 )
...
...
...
...
( n 1)
( n 1)
( x0 )
y2
( x0 ) ...
yn
( n 1)
( x0 )
0.
32.
Пример. Найти определитель Вронскогосистемы функций на указанном
интервале: e x , xe x , x 2e x ; I , .
ex
exx
e x x 1
W ( x) e x
e
x
x2
1
x 1
x 2x
x
x2
e3x 0 1
2x
0
1
1 x 2
1
e x x2 2x
e x x 2 e x x 2 4 x 2
ex
3x
e x x2
2
x 4x 2
2
e 3 x (4 x 2 4 x ) 2e 3 x 0
x ( , ).
2 4x 2







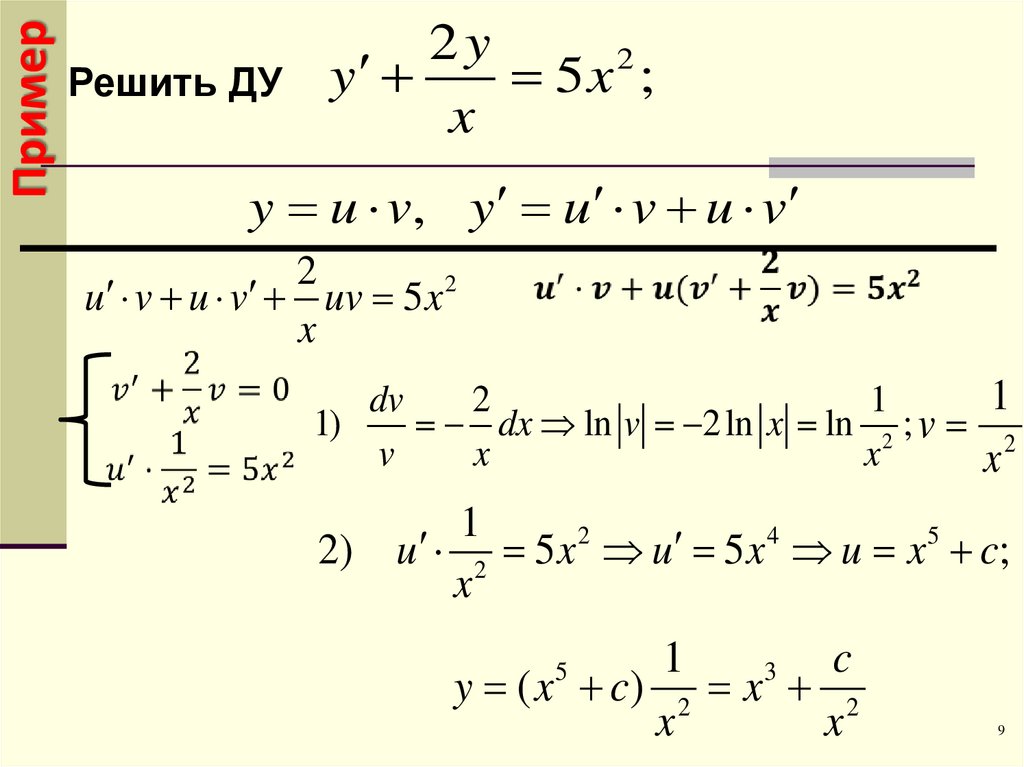

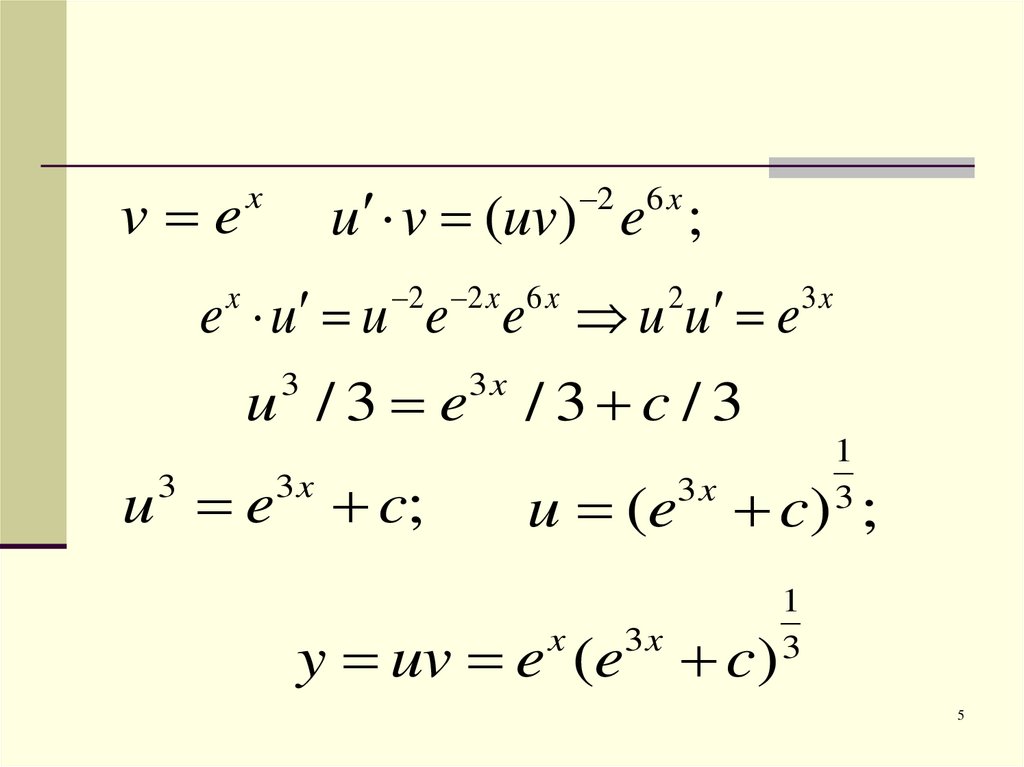
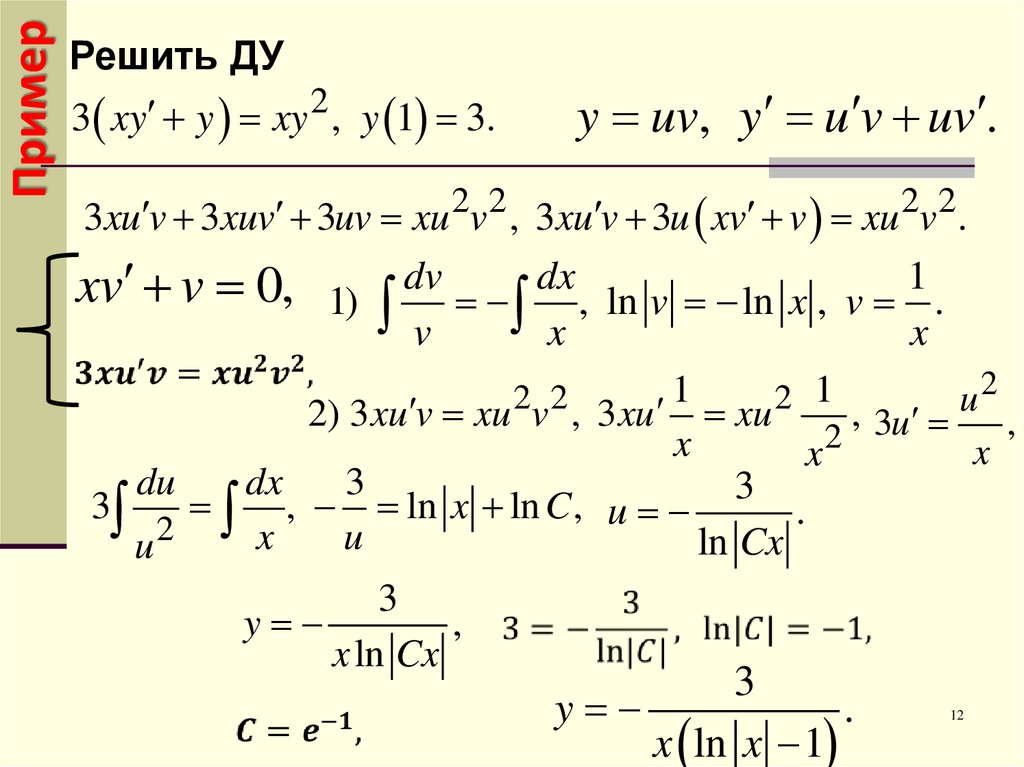
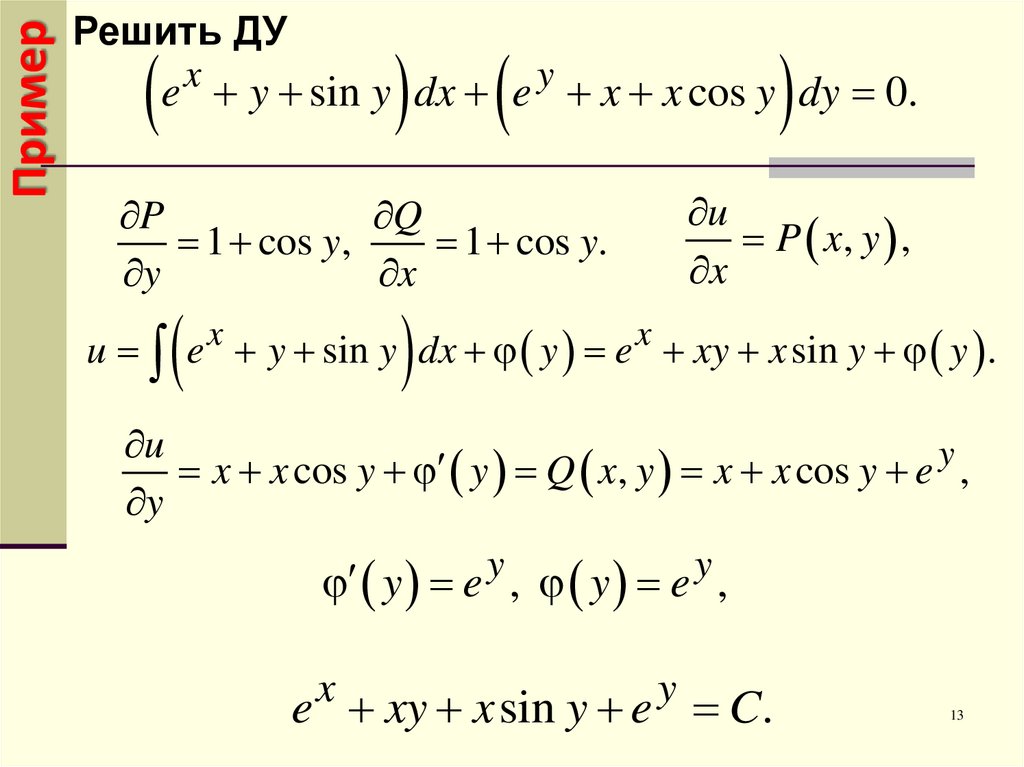






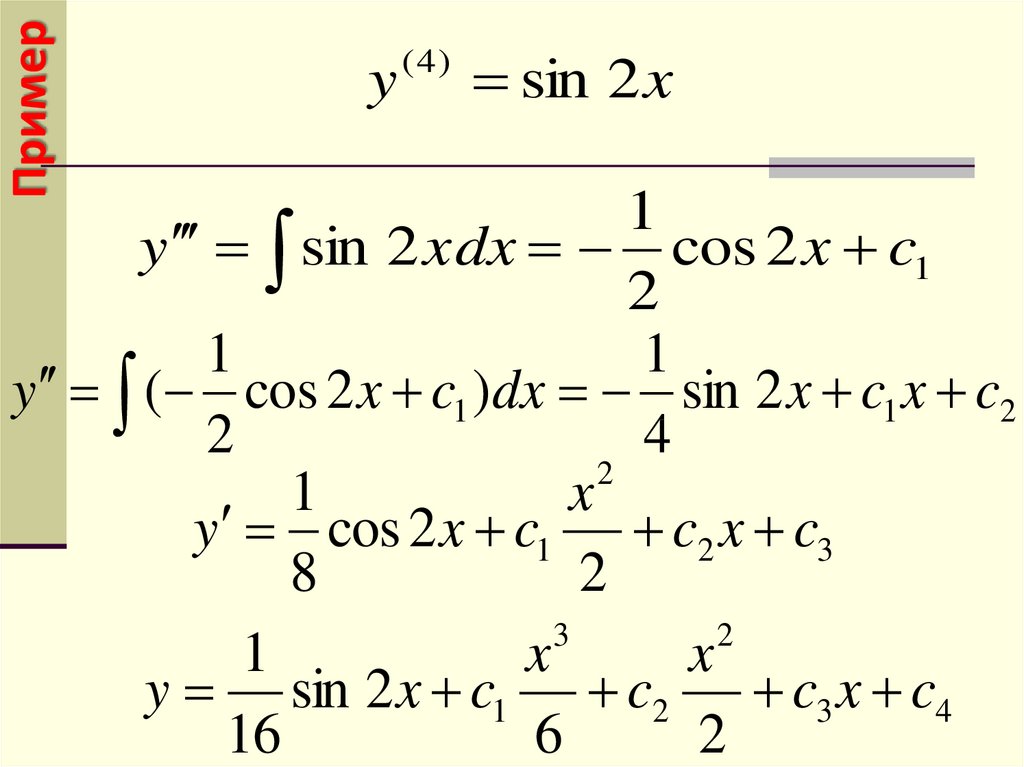
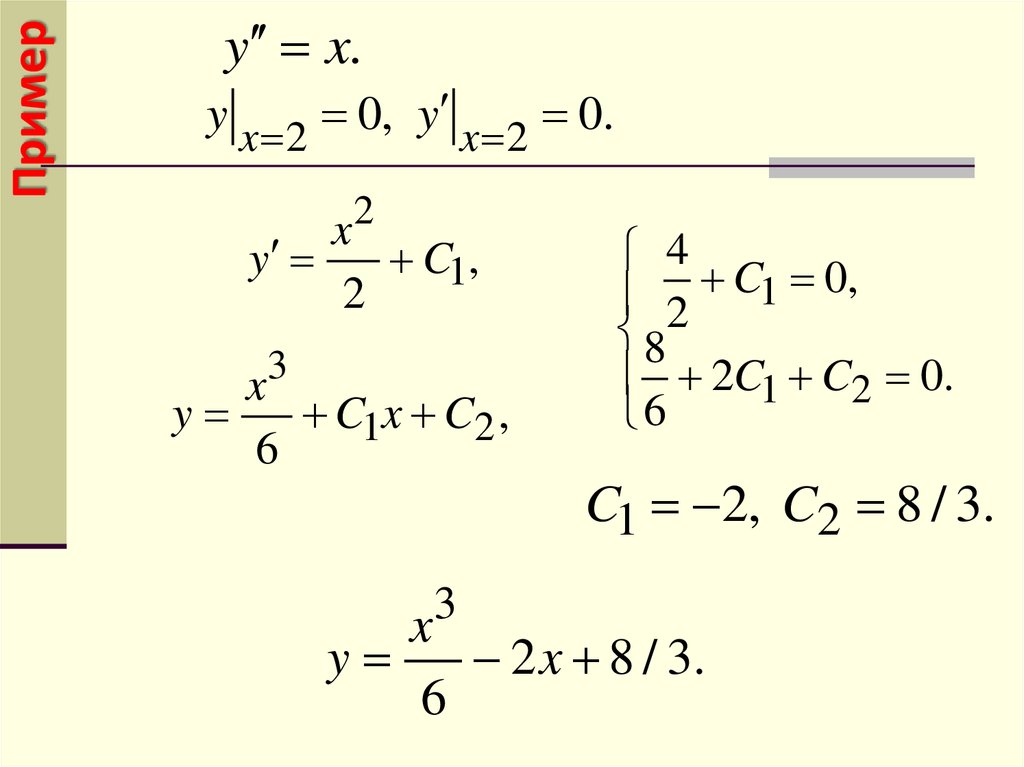

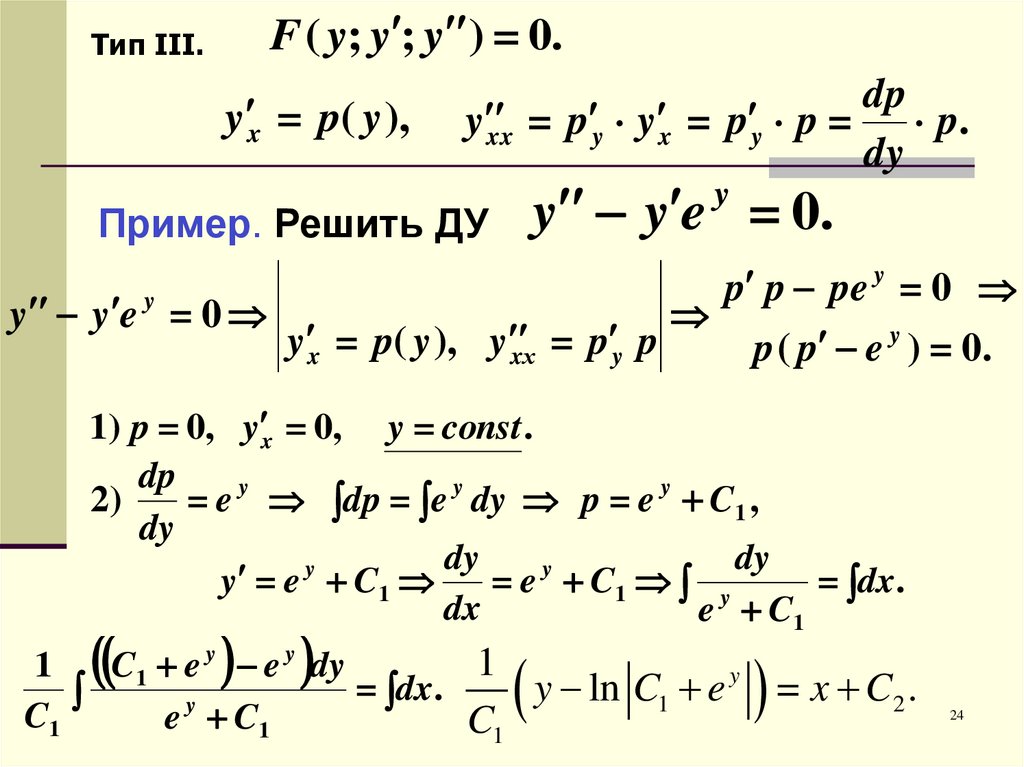




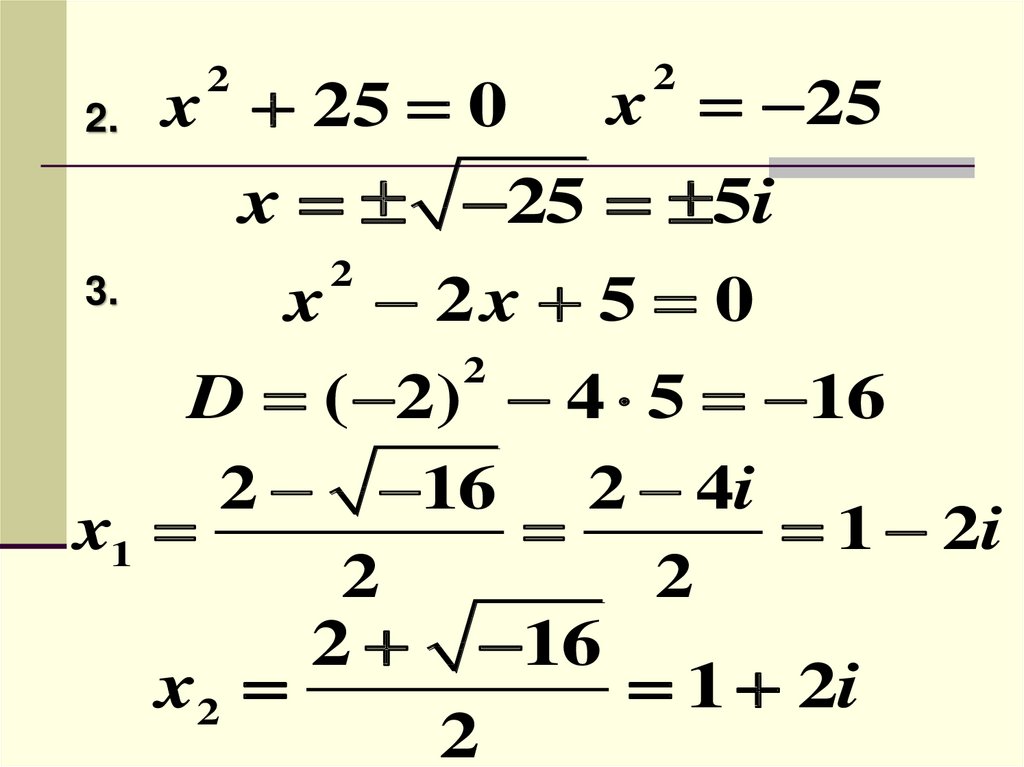




 Математика
Математика








