Похожие презентации:
Тригонометрические неравенства
1. Тригонометрические неравенства
Вопросы:1. Простейшие тригонометрические неравенства.
2. Методы решения тригонометрических неравенств.
2.
Тригонометрическими называются неравенства, вкоторых переменная является аргументом тригонометрической
функции.
Простейшие тригонометрические неравенства:
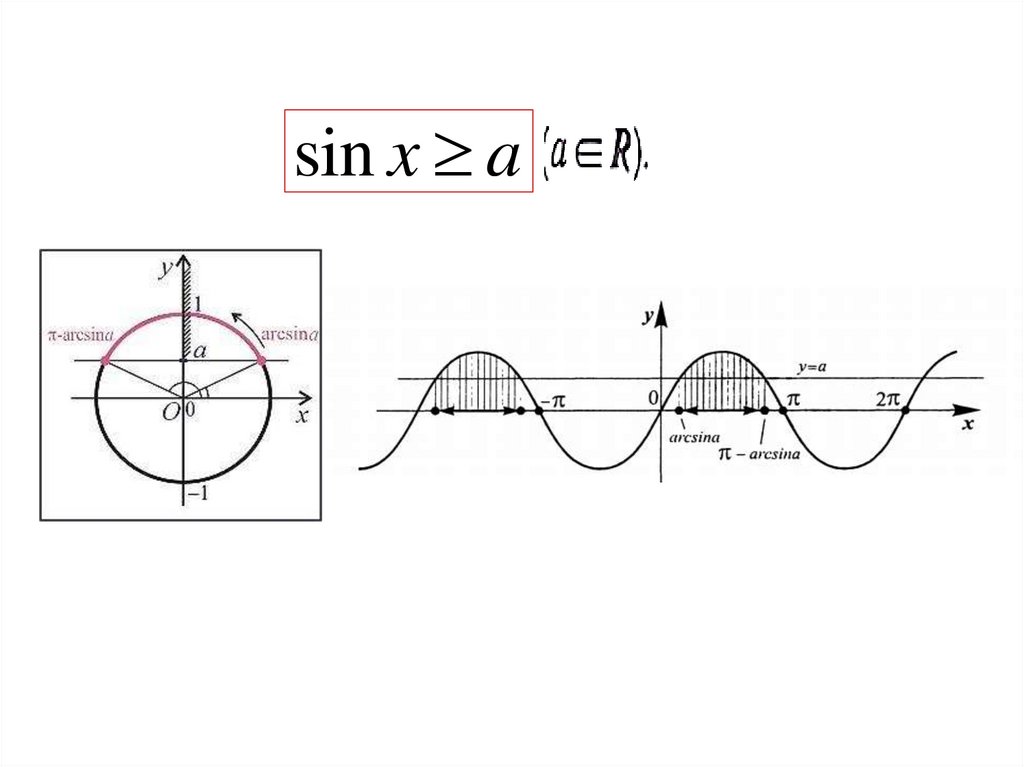
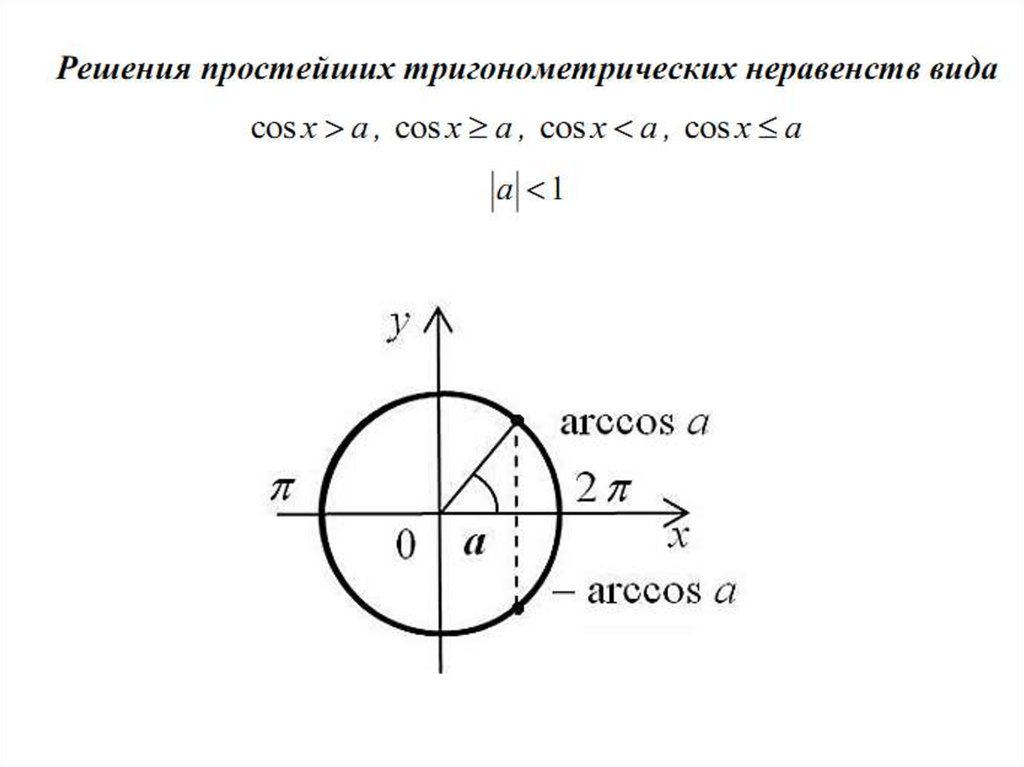
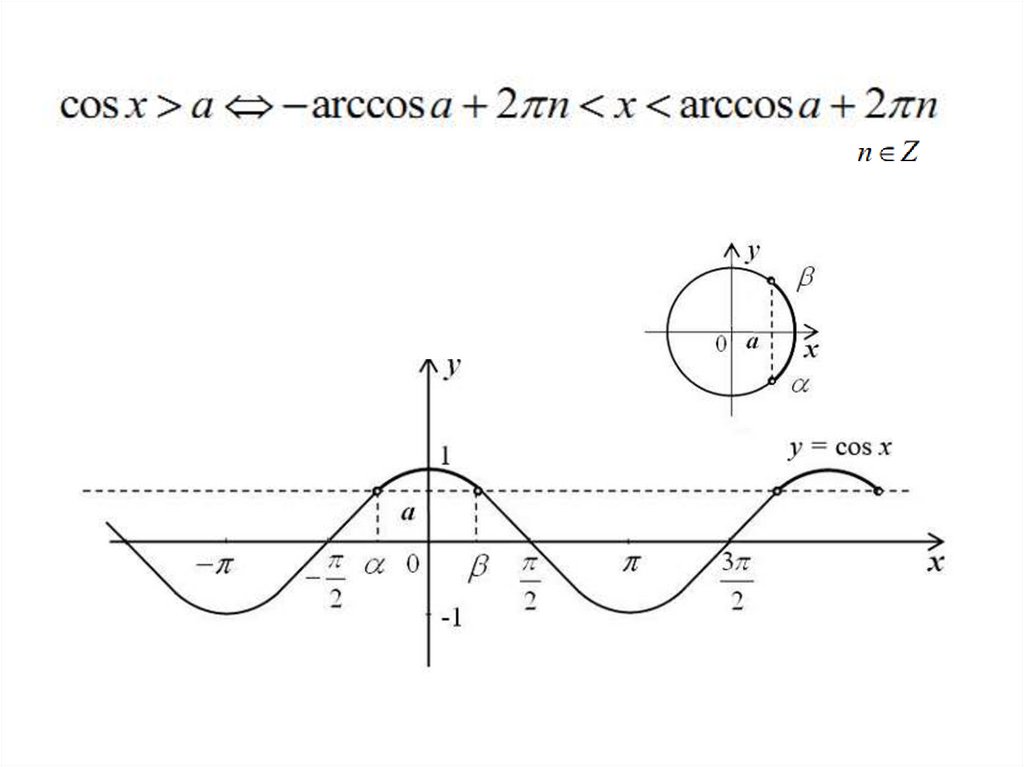
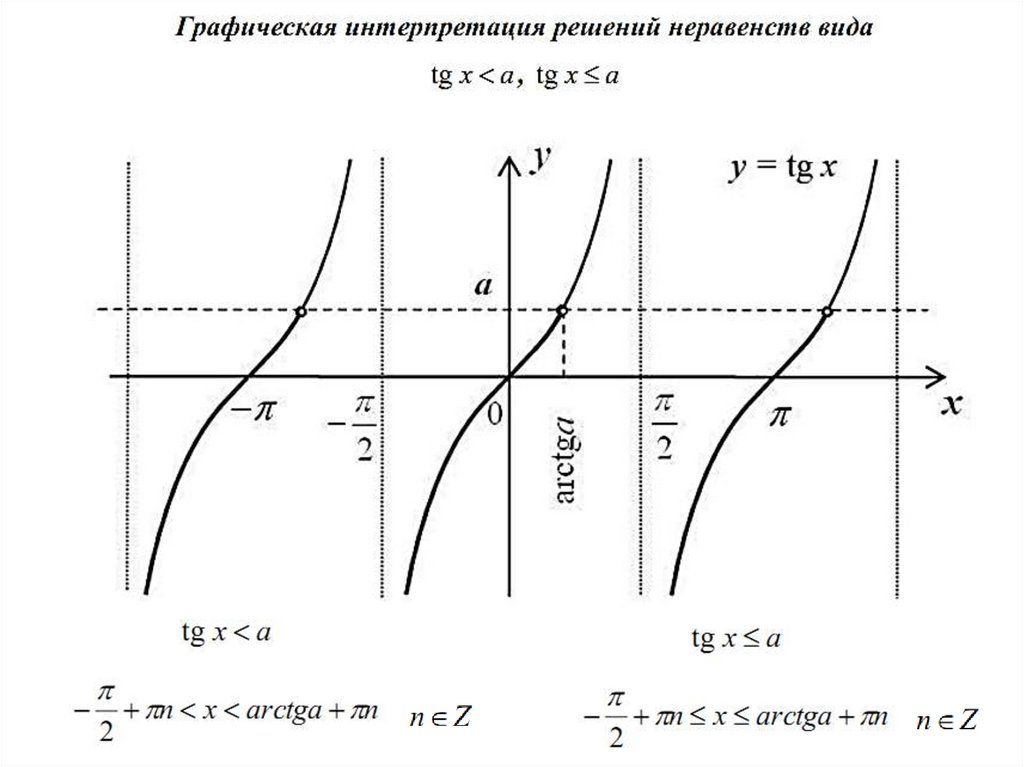
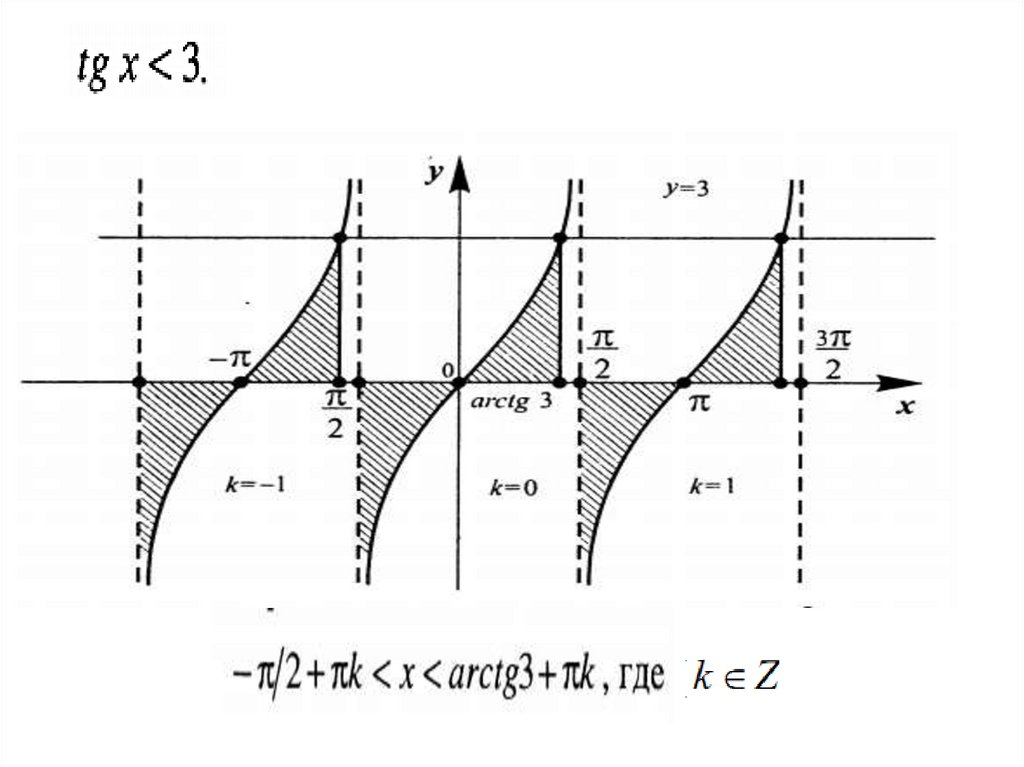
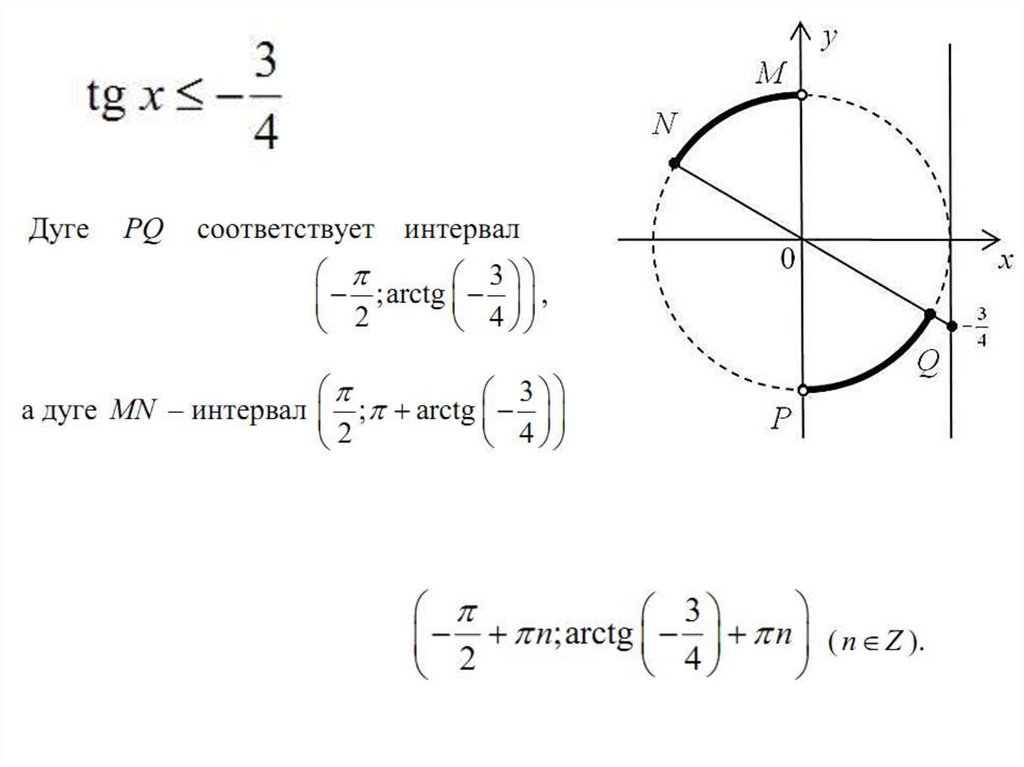
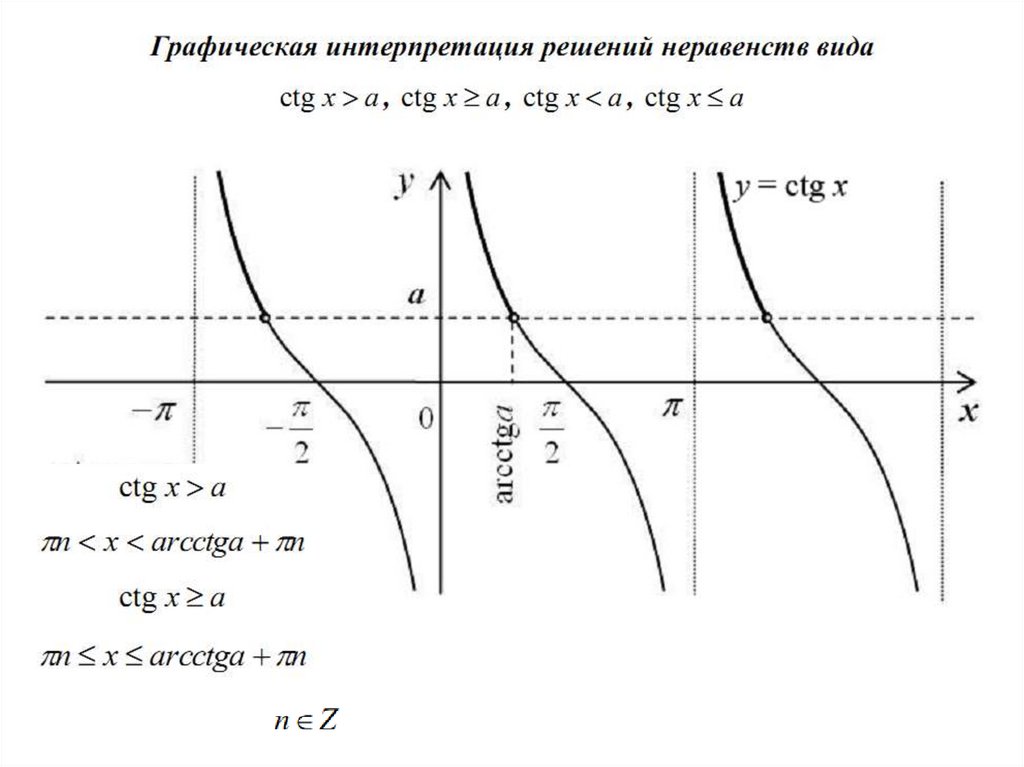
sinx > a, cosx > a, tgx > a, ctgx >a (<, , )
Способы решения простейших тригонометрических
неравенств:
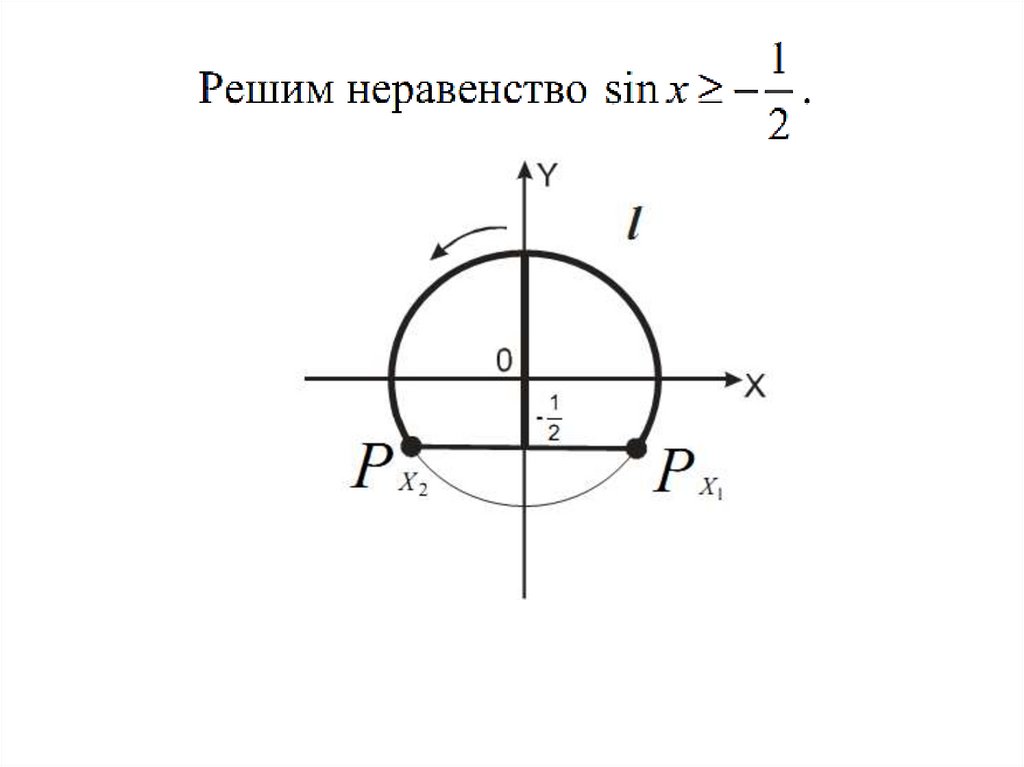
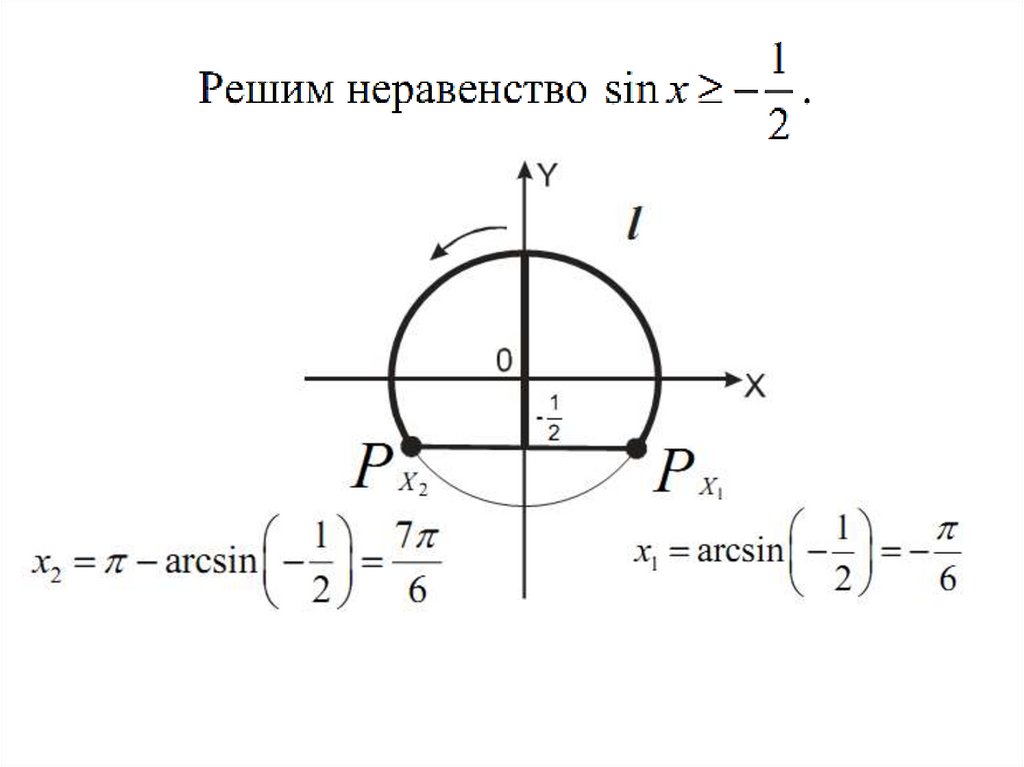
1. с использованием тригонометрической окружности;
2. с использованием графиков тригонометрических функций.
3.
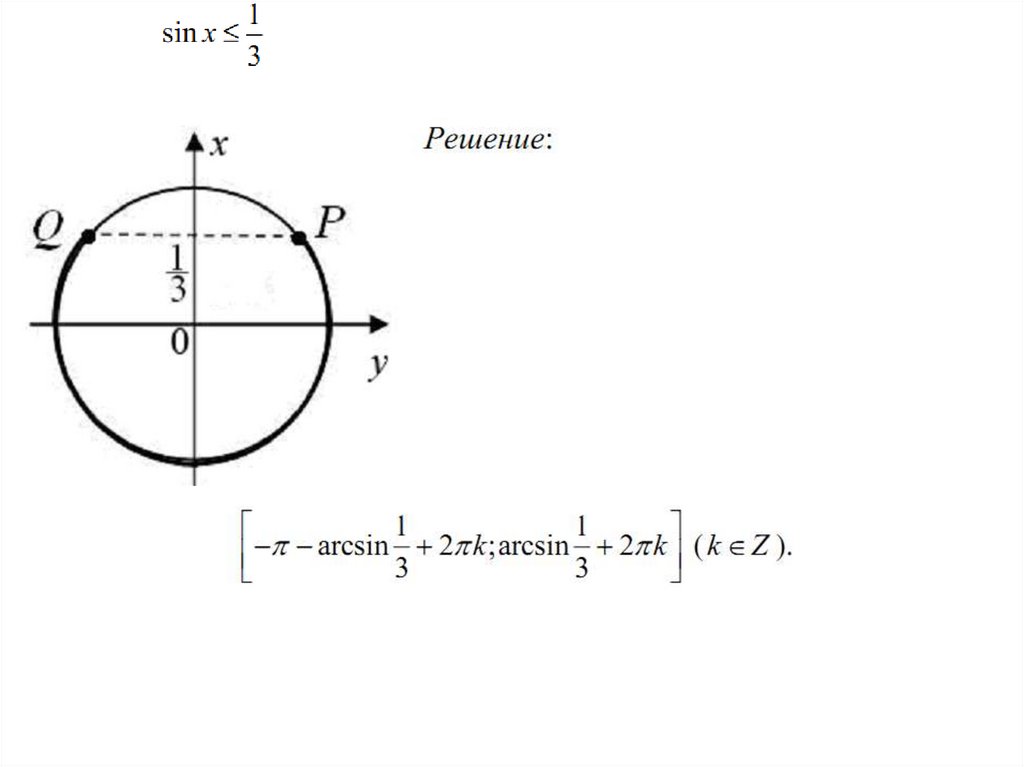
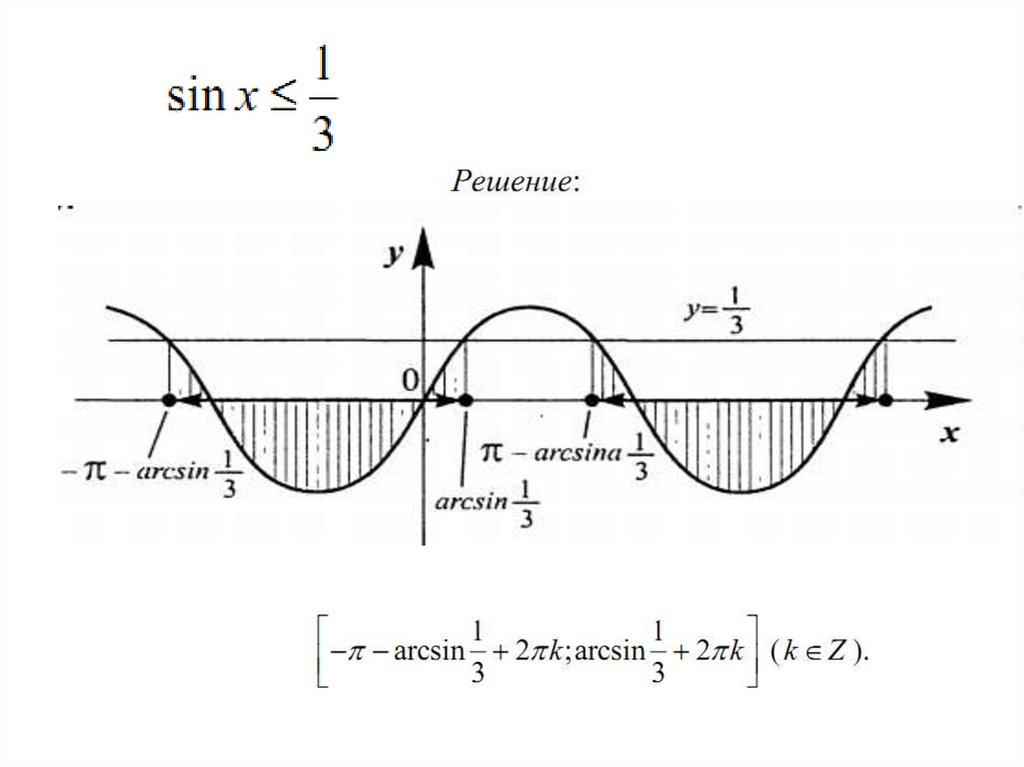
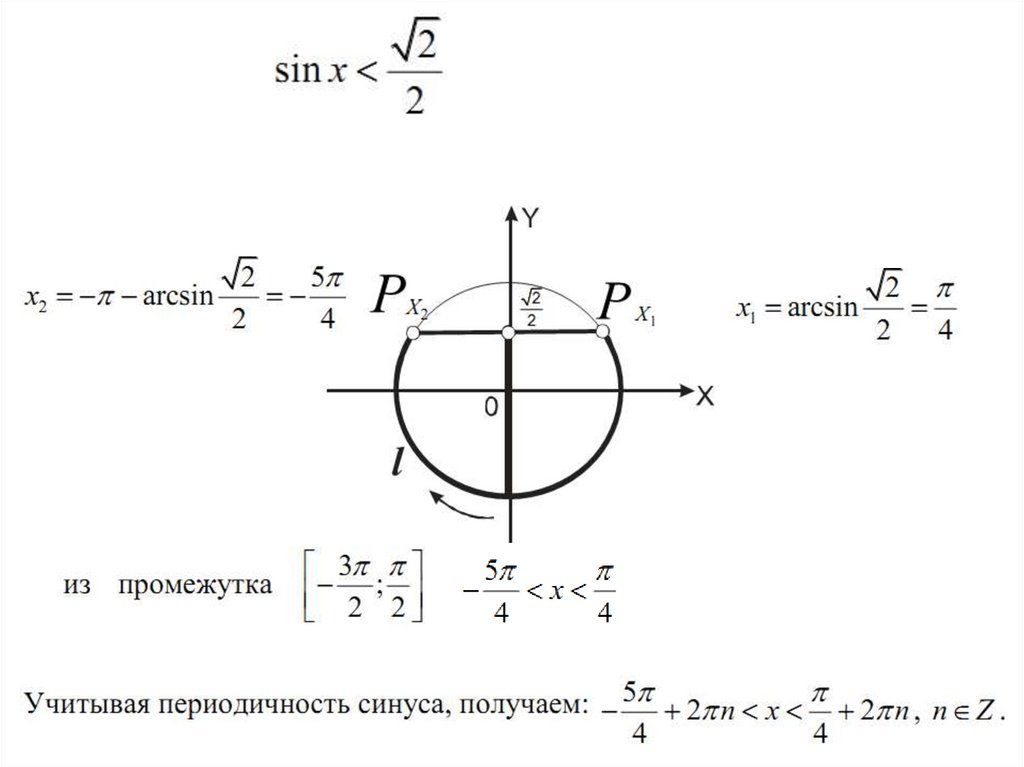
sin x a4.
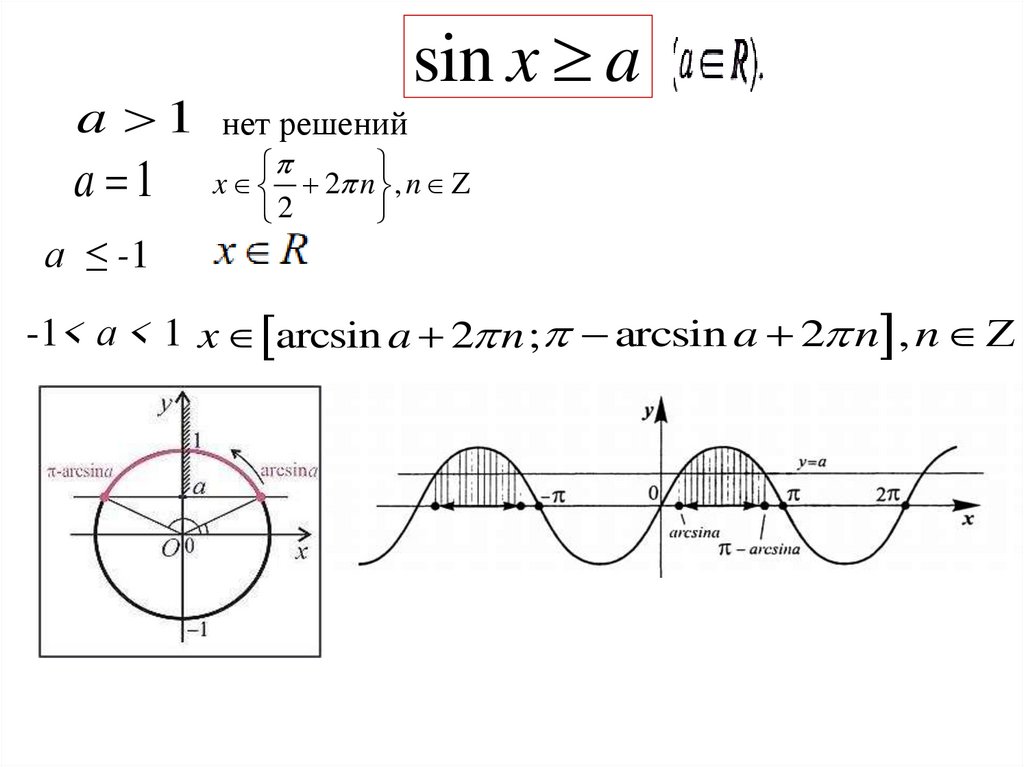
a 1 нет решенийa 1
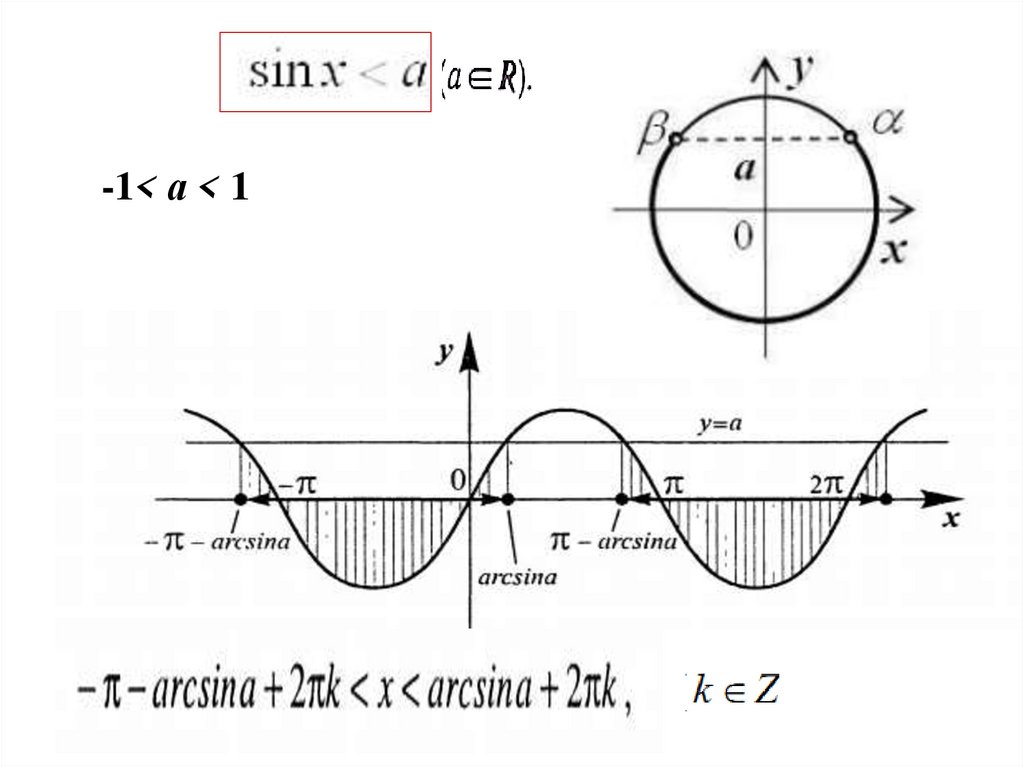
sin x a
x 2 n , n
2
а ≤ -1
-1< а < 1 x arcsin a 2 n ; arcsin a 2 n , n
5.
6.
7.
8.
9.
-1< а < 110.
-1< а < 1a 1
a 1
а ≤ -1
x 2 n , n
2
нет решений
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
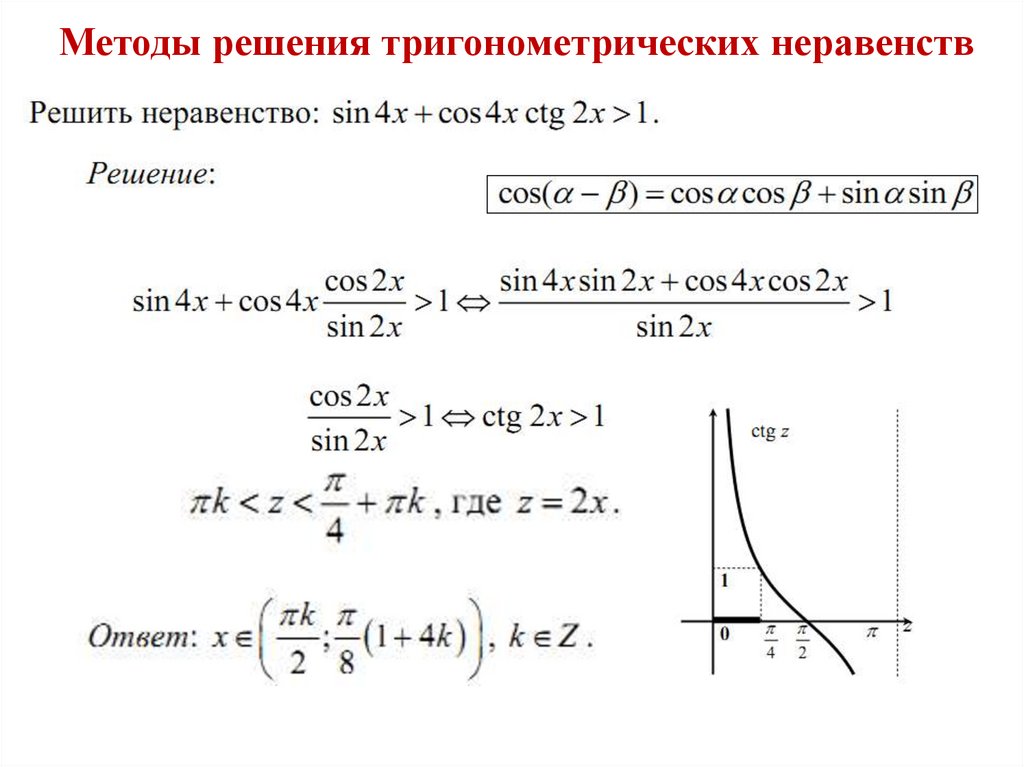
Методы решения тригонометрических неравенств34.
Методы решения тригонометрических неравенств35.
Методы решения тригонометрических неравенств36.
Методы решения тригонометрических неравенств37.
Методы решения тригонометрических неравенств38.
Методы решения тригонометрических неравенств39.
40.
41.
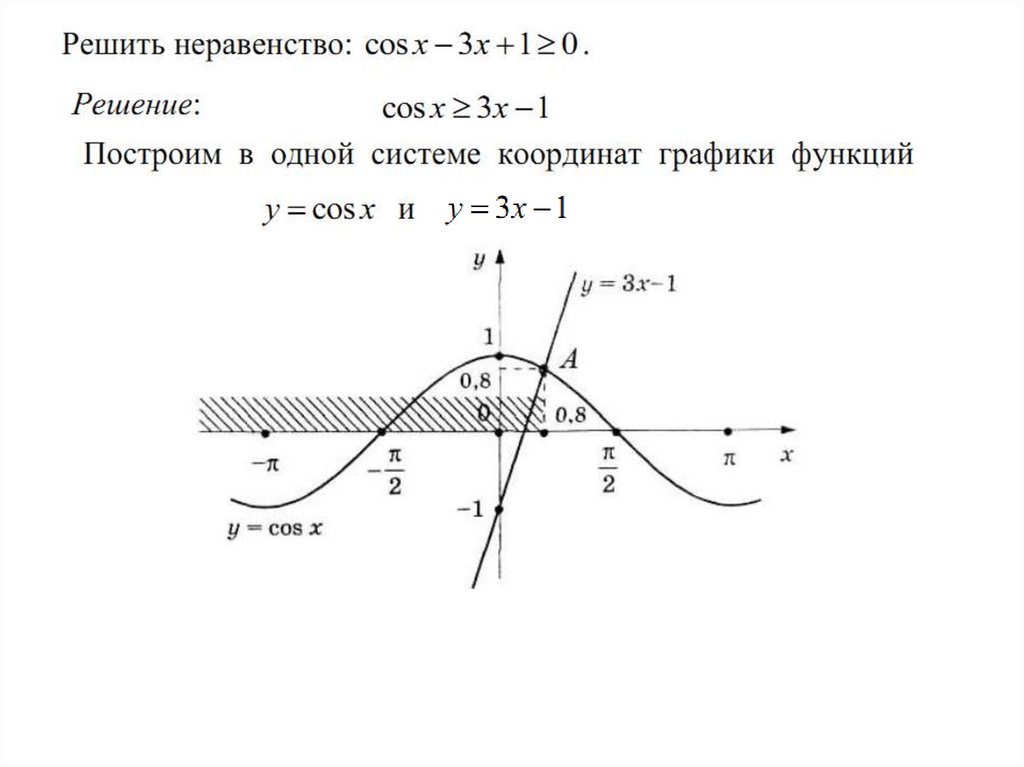
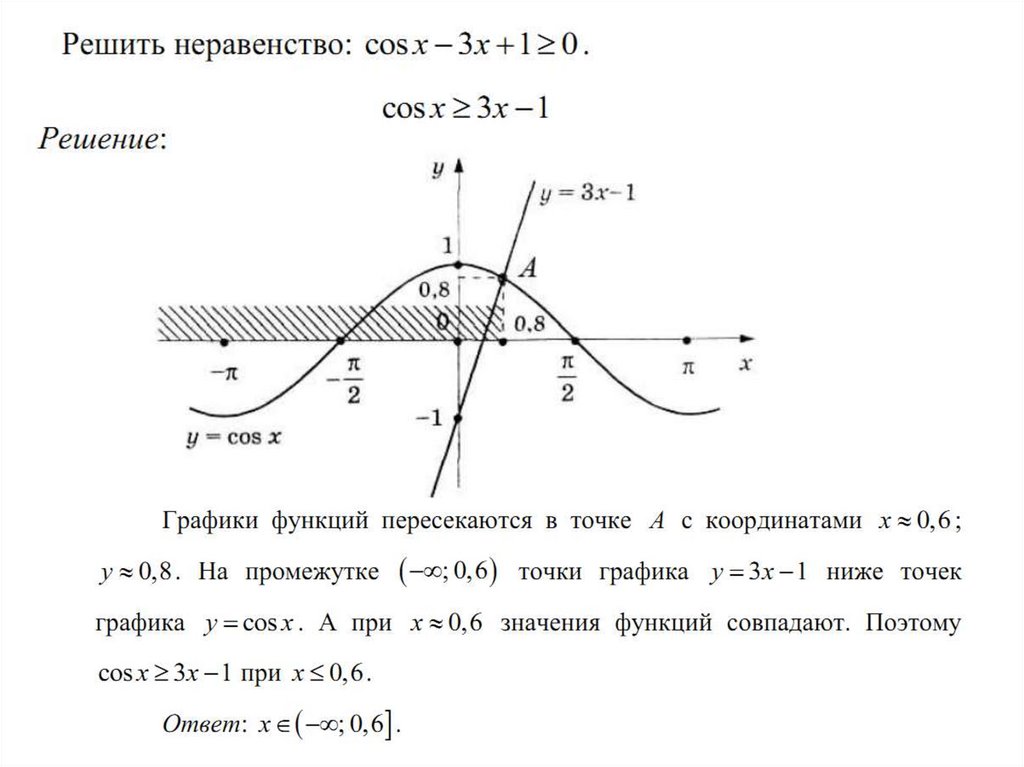
Методы решения тригонометрических неравенств42.
43.
Методы решения тригонометрических неравенств44.
Методы решения тригонометрических неравенств45.
Методы решения тригонометрических неравенств46.
47.
Методы решения тригонометрических неравенств48.
49.
50.
51.
52.
Методы решения тригонометрических неравенств53.
54.
55.
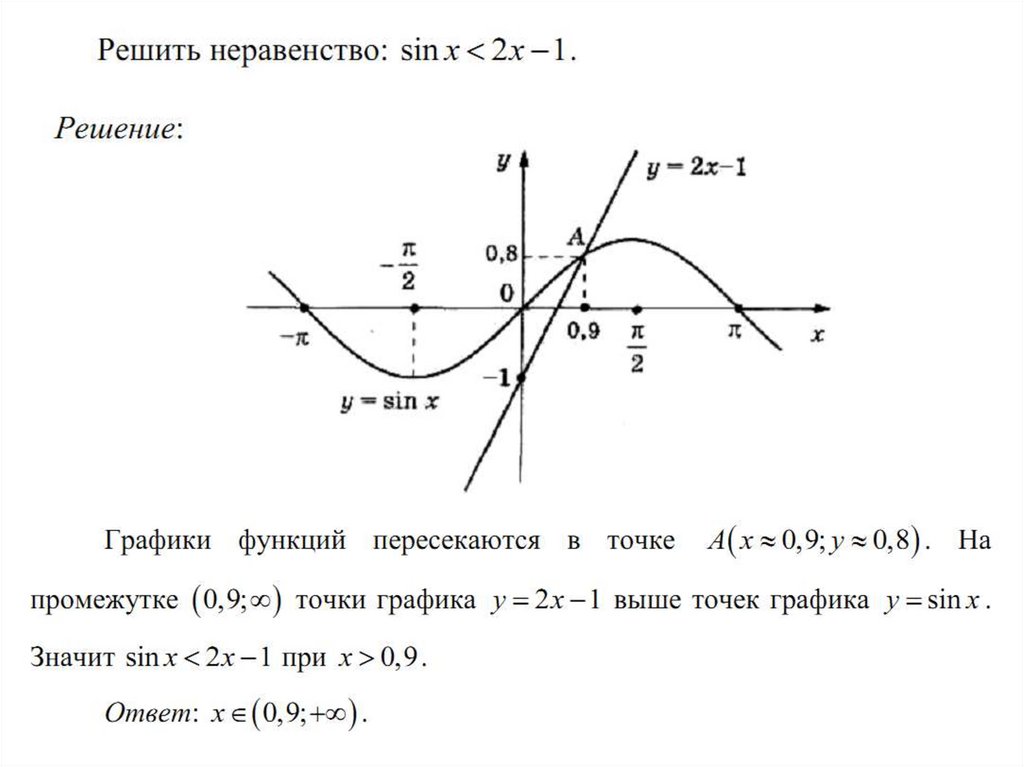
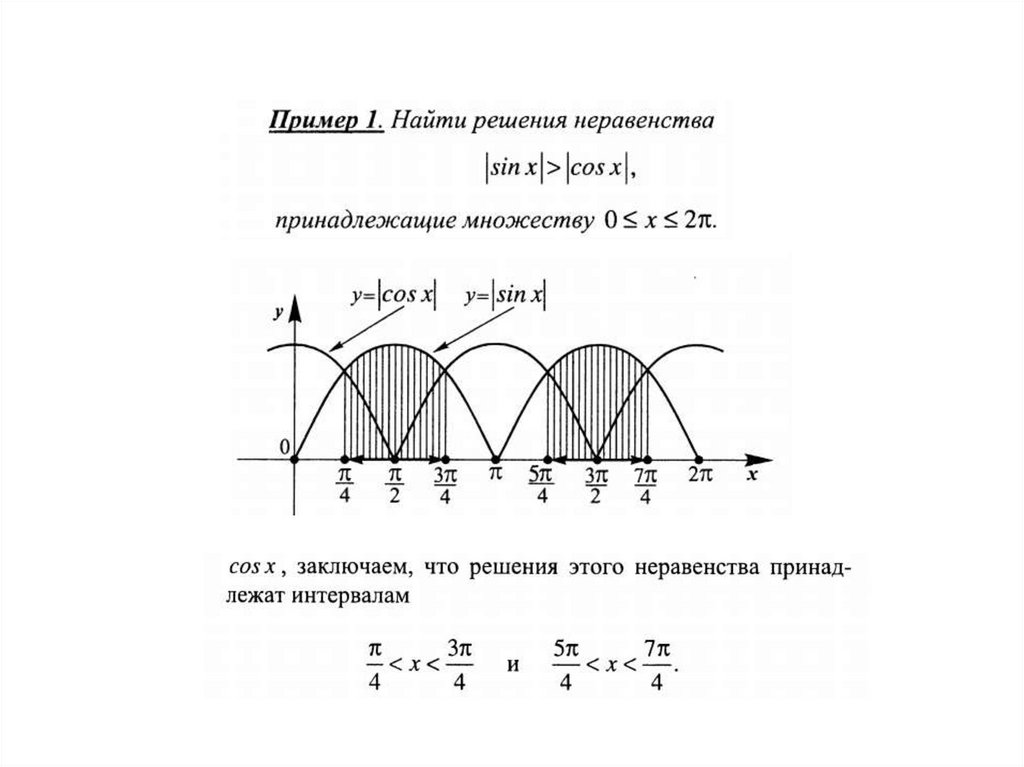
2) Область определения х є R.Найдем нули:
56.
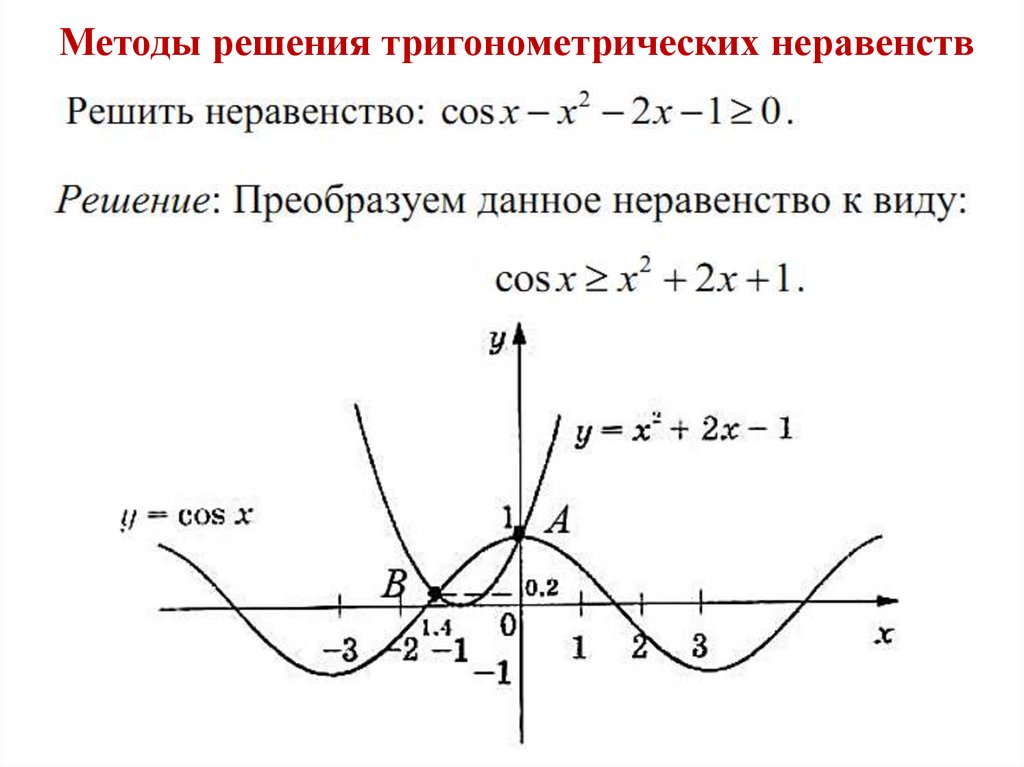
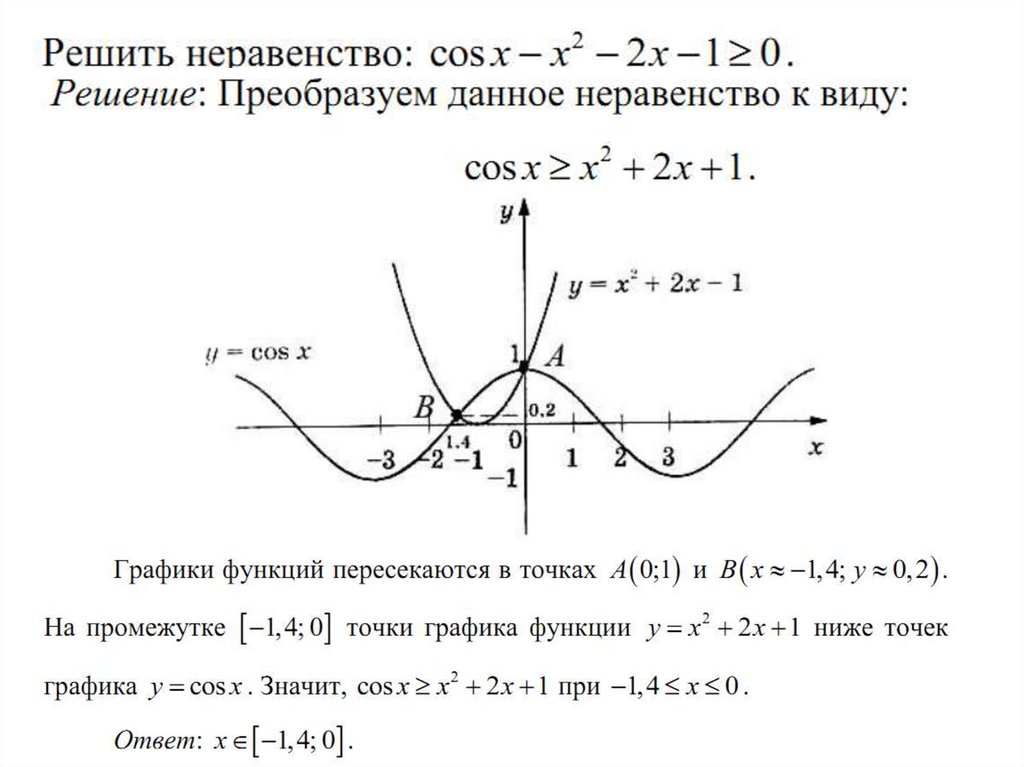
2) Область определения х є R.Найдем нули:
57.
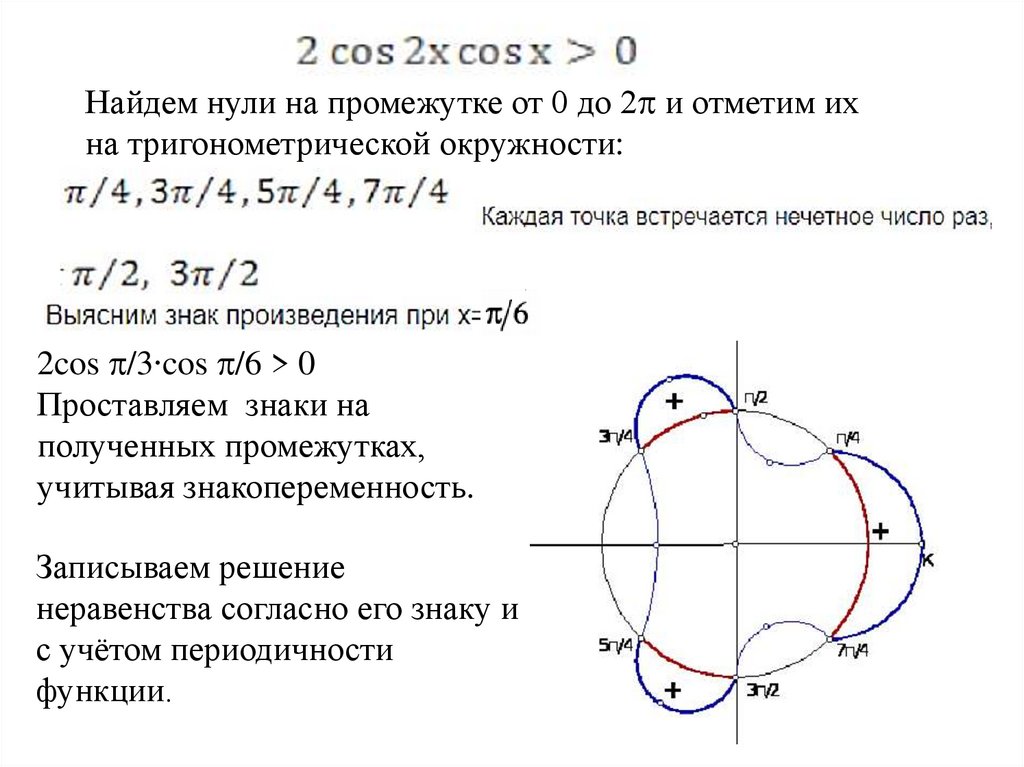
Найдем нули на промежутке от 0 до 2 и отметим ихна тригонометрической окружности:
58.
Найдем нули на промежутке от 0 до 2 и отметим ихна тригонометрической окружности:
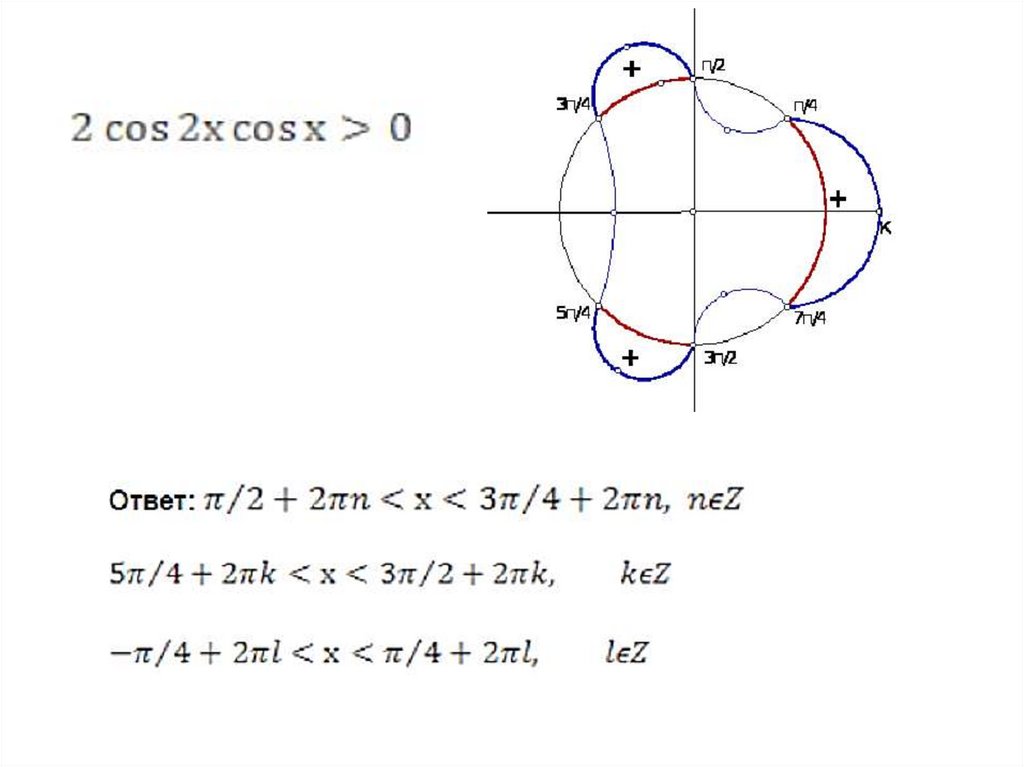
2cos /3∙cos /6 > 0
Проставляем знаки на
полученных промежутках,
учитывая знакопеременность.
Записываем решение
неравенства согласно его знаку и
с учётом периодичности
функции.





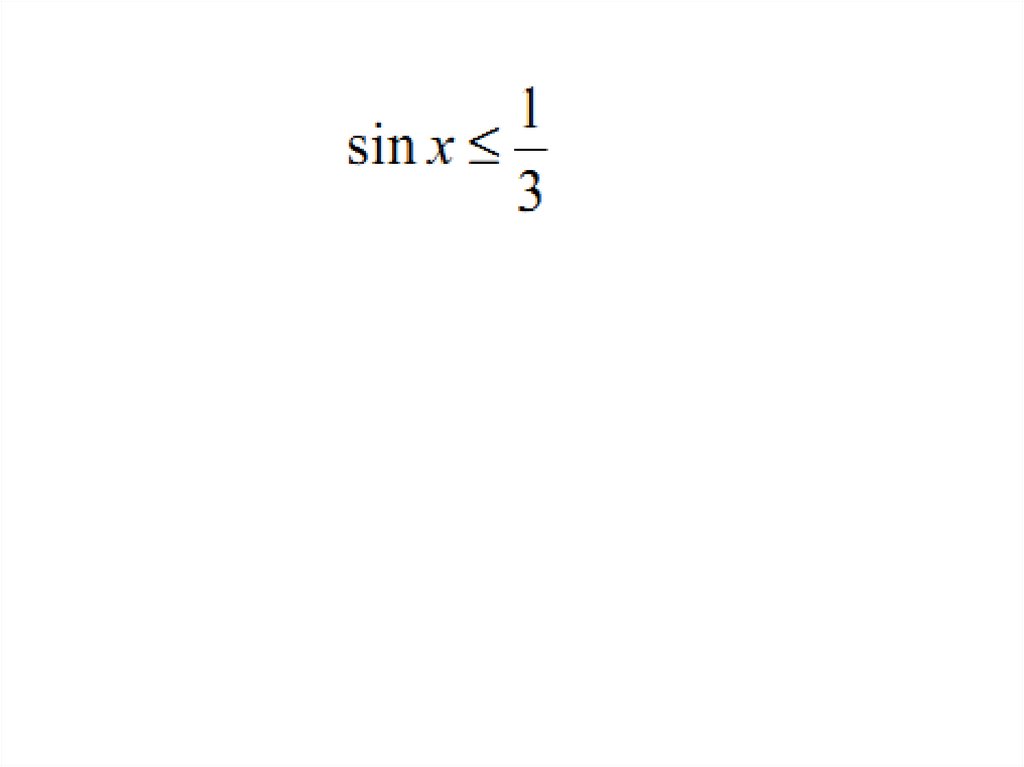







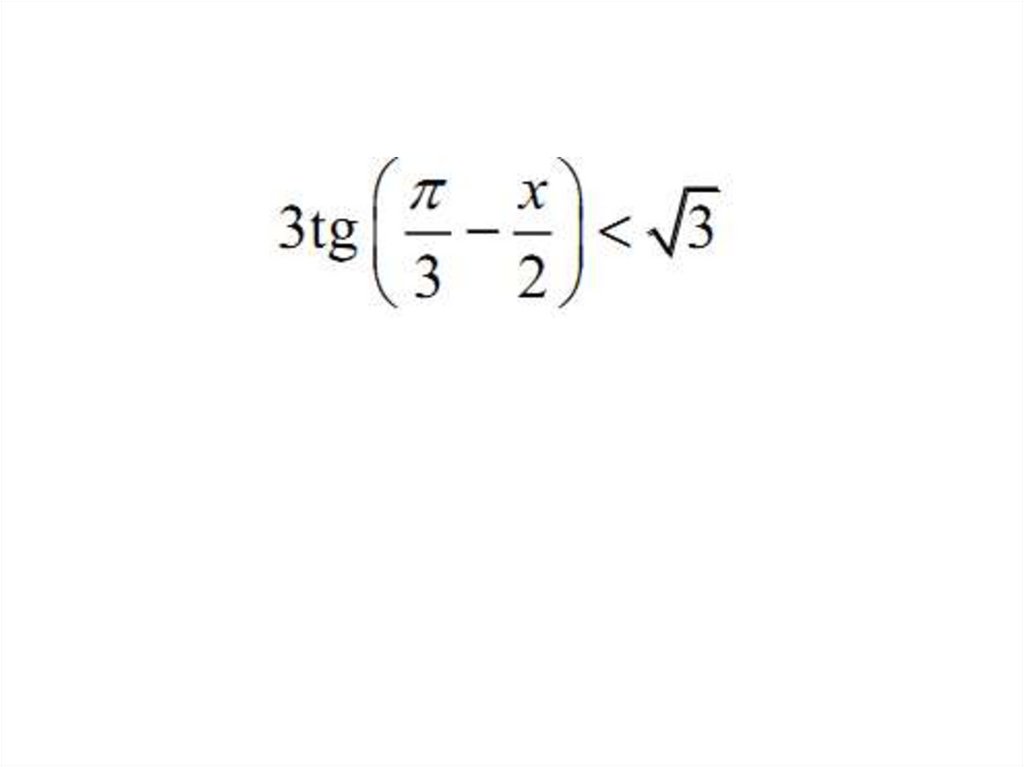


























 Математика
Математика








