Первообразная и неопределенный интеграл

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
Раздел: Неопределенный интеграл
Лекция 7.
Первообразная и
неопределенный интеграл
24.05.2025
г. СанктПетербург
2025
1/12

2.

Содержание лекции
1. Определение первообразной функции.
2. Неопределенный интеграл (НИ).
3. Свойства НИ
4. Таблица основных интегралов
2|12

3.

?
ПЕРВООБРАЗНАЯ
Найти функцию f(x) по ее производной f ’(x)
Восстановить закон движения S = S(t), если задана скорость: S’(t) = V(t)
Функция F (x ) – первообразная для функции f (x) на (a,b), если во всех точках
выполняется равенство:
F ' ( x) = f ( x)
dF(x) = f(x)dx
dF ( x)
dx
Tеорема. Если F1(x) и F2(x) – какие либо две первообразные для функции f(x)
на (a; b), то F1(x) F2(x) = С x (a; b) , где C=const.
Любые две первообразные отличаются на постоянную величину
По условию F1’(x) = F2’(x) = f(x)
Составим функцию Ф(x) = F1(x) – F2(x) – дифференцируема
Ф’(x) = F1’(x) – F2’(x) = 0
Ф’(x)= 0 x (a; b) Ф(x) = const F1(x) F2(x) = C
3|12

4.

Вывод: если F(x) – первообразная для f(x) на (a; b), то любая другая первообразная
+C
Ф(x) для f(x) на (a; b) имеет вид:
1
Пример. Для функции f(x) = x 2
Ф(x) = F(x) + C
найти первообразную, график которой
проходит через точку M(1; 2)
Совокупность всех первообразных
1
F(x) = - + С
F(1) = 2
x
2 = – 1+С
Совокупность всех первообразных для функции f(x)
на промежутке (a; b) называют неопределённым
интегралом от функции f и обозначают:
Если F(x) – одна из первообразных , то
F(x) = 3 -
1
x
f
(
x
)
dx
ò
ò f ( x)dx = F ( x) + C
подынтегральное выражение
дифференциал
первообразной
4|12
f(x)dx =F’(x)dx=dF(x)

5.

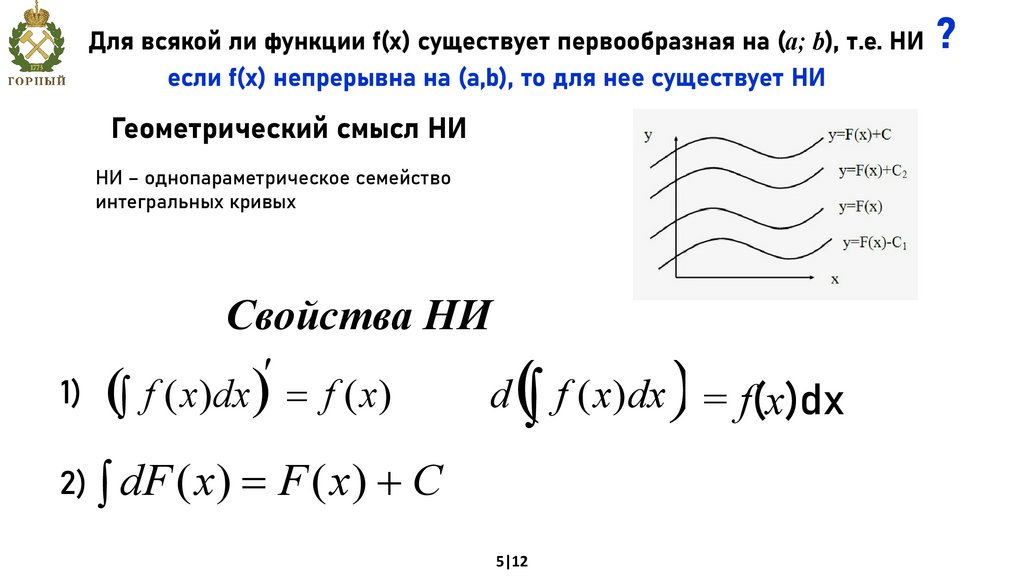
Для всякой ли функции f(x) существует первообразная на (a; b), т.е. НИ
если f(x) непрерывна на (a,b), то для нее существует НИ
Геометрический смысл НИ
НИ – однопараметрическое семейство
интегральных кривых
Свойства НИ
1)
¢
(ò f ( x)dx ) = f ( x)
(
)
d ò f ( x)dx = f(x)dx
2) ò dF ( x ) = F ( x ) + C
5|12
?

6.

3) ∫к f(x)dx = к ∫f(x)dx + C
k = const 0: постоянный множитель можно выносить за знак интеграла
4) ò [f 1 ( x) ± f 2 ( x)]dx = ò f 1 ( x)dx ± ò f 2 ( x)dx
НИ от алгебраической суммы 2-х функций равен алгебраической сумме интегралов от них
Свойство
[
af1 ( x) ± bf 2 ( x)]dx = a ò f1 ( x)dx ± b ò f 2 ( x)dx
ò
линейности:
5) Если F(x) - первообразная для f(x), то ∫f(ax +b)dx =
¢
æ1
ö 1 ¢
ç F(ax + b) ÷ = F (ax + b)a = f(ax +b).
èa
ø a
6|12
1
F(ax +b) + C
a

7.

1
ò f (ax)dx = F (ax) + C ;
a
.
ò f ( x)dx = F ( x) + C
f
(
x
+
b
)
dx
=
F
(
x
+
b
)
+
C
,
ò
1
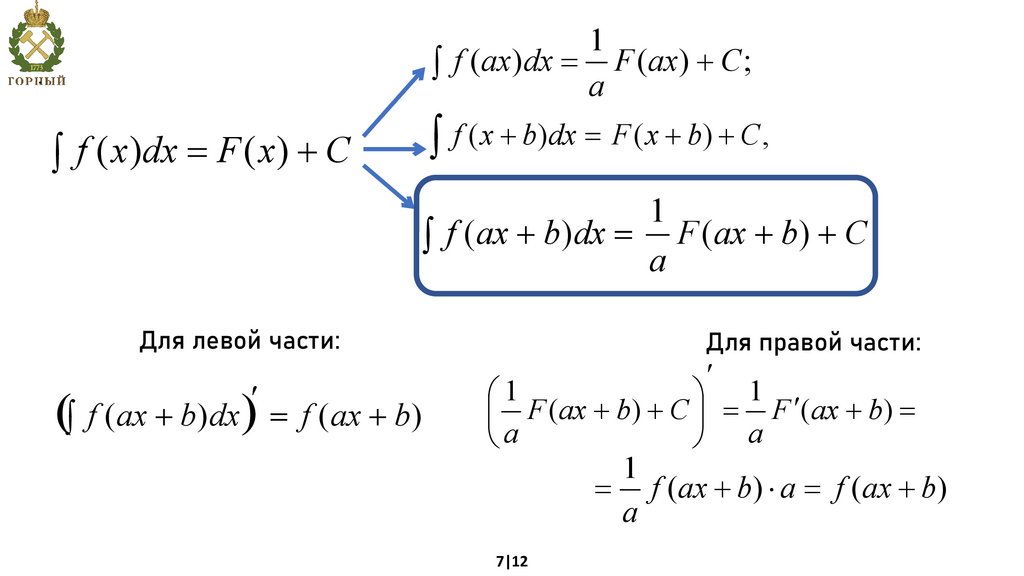
ò f (ax + b)dx = F (ax + b) + C
a
Для левой части:
¢
(ò f (ax + b)dx ) = f (ax + b)
Для правой части:
¢
æ1
ö 1
ç F (ax + b) + C ÷ = F ¢(ax + b) =
èa
ø a
1
= f (ax + b) × a = f (ax + b)
a
7|12

8.

Таблица основных интегралов
1.
x
a = const
a
х
+ C , a > 0, a ¹ 1
8. ò а dx =
ln a
ò dx = x + C.
m +1
x
ó m
+C
2. ô x dx =
m +1
õ
x
x
e
dx
=
e
+ C.
9. ò
m = const, m –1.
10. ò tg xdx = - ln cos x + C
ó dx = ln x + C.
3. ô
õ x
4. ò sin xdx = - cos x + C.
11.
ò ctg xdx = ln sin x + C
ó dx = 1 arctg x + C
12. ô 2
a
õ x + a2 a
5. ò cos xdx = sin x + C.
13. ó
x
= arcsin + C
ô
a
õ a2 - x2
dx
ó
= tg x + C.
6. ô
2
õ cos x
ó dx = - ctg x + C.
7. ô
õ sin 2 x
dx
dx
1
x-a
=
ln
+ C, a ¹ 0
ô 2
2
2a x + a
õ x -a
14. ó
8|12

9.

ó
15. ô
õ
16.
17.
ò(
dx
x2 + m
= ln x + x 2 + m + C , m ¹ 0.
ò sh xdx = ch x + C.
18.
ò ch xdx = sh x + C.
19.
ó dx = th x + C.
ô 2
õ ch x
ó dx = - cth x + C.
ô 2
õ sh x
Пример 1. Найти интеграл
)
6
2
x
x
6 x 5 - 2 x + 1 dx = 6ò x 5 dx - 2ò xdx + ò dx = 6 - 2 + x + C = x 6 - x 2 + x + C
6
2
1
ò cos 7 xdx = 7 sin 7 x + C
9|12

10.

( )
2
×
3
dx
= ò 2×3
ò
x
2x
2 x
x
18
dx = 18 dx =
+C
ln 18
ò
Методы интегрирования
x
1. Непосредственное интегрирование – через
алгебраические преобразования подынтегральной функции и
свойства НИ подвести к табличным интегралам
Пример 2. Найти интеграл
ó (1 + x 2 ) - x 2
ó dx
dx
ô 4
2 = ô
2
2
õx +x
õ x ( x + 1)
dx ó dx
ó
=ô 2 - ô
õ 1+ x2
õx
1
ò x dx = - x
-2
10|12
1
= - - arctg x + C
x

11.

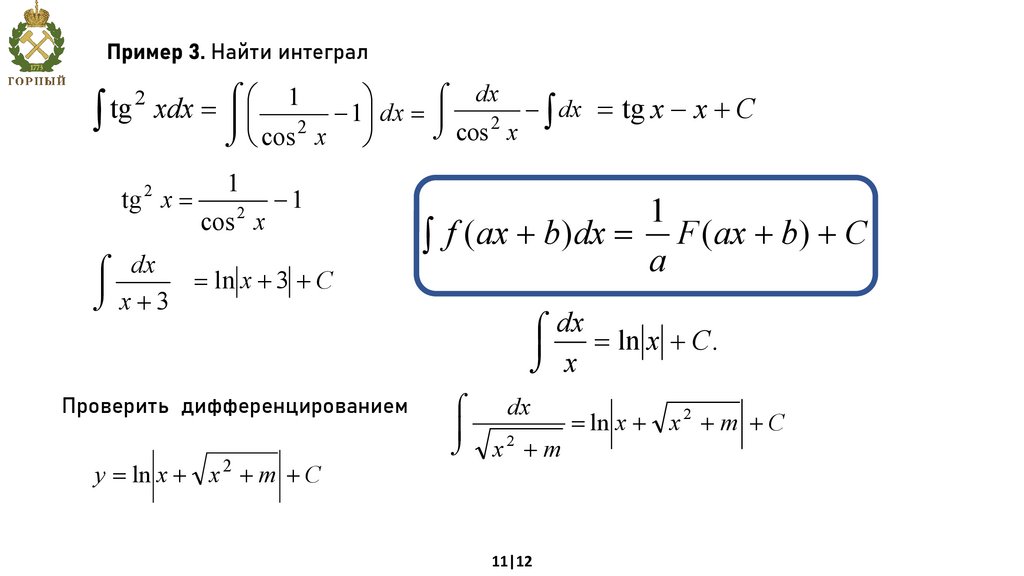
Пример 3. Найти интеграл
ò
1
ó dx - dx
ó
æ
ö
tg xdx = ô ç
= tg x - x + C
1
dx
=
÷
ô
ò
2
2
õ cos x
õ è cos x ø
2
1
tg x =
-1
2
cos x
2
ó dx = ln x + 3 + C
ô
õ x+3
Проверить дифференцированием
y = ln x + x 2 + m + C
1
ò f (ax + b)dx = F (ax + b) + C
a
ó dx = ln x + C.
ô
õ x
ó
ô
õ
dx
x2 + m
11|12
= ln x + x 2 + m + C

12.

Спасибо за внимание
Санкт-Петербургский горный
университет
императрицы Екатерины II,
г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
12|12