Интегрирование иррациональных и тригонометрических выражений

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
Раздел: НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Лекция 10–11
24.05.2025
ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ И
ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
кафедра высшей математики
1/20

2.

Основной прием – рационализация
подынтегрального выражения
найти замену
переменной
подынтегральное выражение приняло
рациональный вид
1. Рассмотрим интеграл
ò R (x, x
mn
,....x
r s
)dx
k – общий знаменатель дробей
{m n ,....., r s}
x=t
рациональная функция
k
dx = kt
k -1
dt
5
2 ö
ó x dx ó x1 2 dx
óæ 2
ó t2 3
t
t
ó
÷dt
I =ô
= 4ô 3
t dt = 4ô
= 4ô ç t - 3
=ô 34
dt
ç
÷
3
4 3
t
+
1
õ t +1
õ t +1
õè
ø
õ x +1 õ x +1
x=t
k=4
x
12
=t
2
4
3
dx = 4t dt
x3 4 = t 3
3
2
4
t
t
ó
3
2
ln
t
+1 + C
4
= 4 ò t dt - 4ô 3
dt =
3 3
õ t +1
[
]
4 34
I = x - ln x 3 4 + 1 + C
3
2/20

3.

2. Интегралы вида:
ó æ æ ax + b ö
÷
ô R çç x, ç
ô
õ è è cx + d ø
рациональная функция
mn
æ ax + b ö
,...., ç
÷
è cx + d ø
r s
ö
÷ dx
÷
ø
Выразить х
2
x
=
1
t
dx
ó
I =ô
dx = -2tdt
õ (2 - x ) 1 - x
2
2 - x = 1+ t
ó 5 - 3x
J =ô
dx
õ 4 + 7x
ax + b k
=t
cx + d
1 - x = t;
5 - 3x
t=
4 + 7x
5 - 4t 2
x=
3 + 7t 2
k – общий знаменатель
дробей
{m n ,....., r s}
ó - 2tdt = -2 arctg t + C = -2 arctg 1 - x + C
=ô 2
õ t +1 t
(
)
5 - 3x
t = 4 + 7x
2
dx =
- 94tdt
(3 + 7t )
2 2
ó
2
- 94t
ó
t
= ôt
dt
= -94ô
dt
2
2
ô 2
õ 7t 2 + 3
õ 7t + 3
(
u = t;
dv =
3/20
)
(
du = dt ;
tdt
(7t + 3)
2
2
1
1
v=14 7t 2 + 3
)

4.

формула М.В. Остроградского при n ³ 2
3. Интегралы вида
Pn ( x)dx
ó
ô
õ ax 2 + bx + c
ó
dx
= Qn-1 ( x) ax + bx + c + λô
õ ax 2 + bx + c
Многочлен с неопределенными
некоторое
коэффициентами
число
2
Найти неопределенные
коэффициенты многочлена
и число :
приводится к табличному
выделением полного
квадрата под знаком
радикала
1) продифференцировать по х
2) умножить обе части полученного равенства на
ax 2 + bx + c
3) сравнить в полученном выражении коэффициенты
при одинаковых степенях х
ó
I =ô
õ
ó
dx = (Ax + B ) x + 2 x + 3 + λô
x 2 + 2x + 3
õ
x2 +1
2
Многочлен 1–ой степени
4/20
dx
x 2 + 2x + 3

5.

Дифференцируя по х обе
части этого равенства:
x2 + 1
2
x + 2x + 3
= A x + 2 x + 3 + (Ax + B )
Умножаем на
x +1
2
2
x + 2x + 3
Приравниваем коэффициенты
при одинаковых степенях х
ó
I =ô
õ
ó
ó
x2 +1
dx
2
dx =(Ax + B ) x + 2 x + 3 + λô
ô
õ x2 + 2x + 3
õ x2 + 2x + 3
2
x + 2x + 3
(
+
λ
2
x + 2x + 3
.
)
x 2 + 1 = A x 2 + 2 x + 3 + (Ax + B )(x + 1)+ l
x2 :
1 = 2A
x1 :
0 = 3A + B
x0 :
1 = 3A + B + l
ó
1
2
dx = (x - 3) x + 2 x + 3 + ô
2
õ
x 2 + 2x + 3
x2 +1
A=
1
3
, B = - , l =1
2
2
dx
(x + 1)2 + 2
5/20
ln x + 1 + x 2 + 2 x + 3 + C

6.

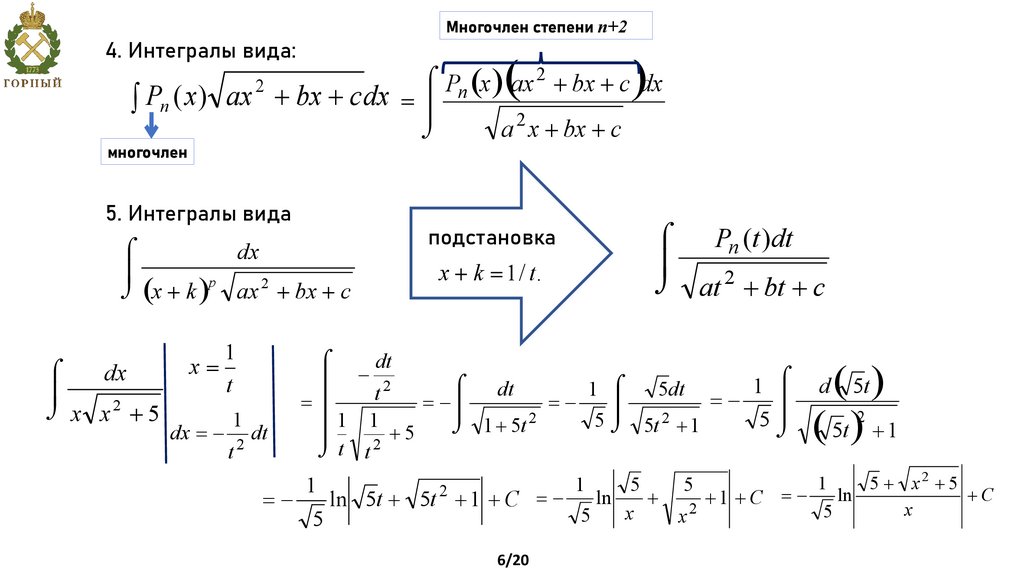
Многочлен степени n+2
4. Интегралы вида:
(
)
ó Pn (x ) aх 2 + bx + c dx
ò Pn ( x) ax + bx + c dx = ô
õ
a 2 x + bx + c
2
многочлен
5. Интегралы вида
ó
dx
ô
õ (x + k )p ax 2 + bx + c
dx
ó
ô
õ x x2 + 5
1
x=
t
1
dx = - 2 dt
t
Pn (t )dt
ó
ô
õ at 2 + bt + c
подстановка
x + k = 1 / t.
dt
ó
ó
ô - 2
ó
1
ó
dt
1
5
dt
t
=ô
=ô
= -ô
=ô
5ô
5 õ 5t 2 + 1
ô 1 1 +5
õ 1 + 5t 2
õ
ô
õ t t2
1
1
5
2
+
=ln 5t + 5t + 1 + C = - ln
x
5
5
6/20
( 5t )
2
( 5t ) + 1
d
5 + x2 + 5
=ln
+C
+
1
+
C
x
5
x2
5
1

7.

6. Интеграл от биномиальных дифференциалов
m
n p
ò x (a + bx ) dx,
m, n, p – рациональные числа
выражается через элементарные функции только в 3-х случаях (П.Л.Чебышев):
подстановка
1) p – целое
x=t
2) m + 1 – целое
n
3)
ó
I =ô
õ
m +1
+p
n
– целое
dx
x
( x + 1)
4
10
s
s – наименьшее общее кратное
знаменателей дробей m и n
n
a + bx = t
s
s – знаменатель
дроби p
b + ax - n = t s
-10
1
1
ö
- æ
1
2
4
x ç x + 1÷ m = - ;
ç
è
1
n = ; p = -10
2
4
÷
ø
7/20
Интеграл
от
рациональной
функции
x=t
4
dx = 4t 3 dt

8.

ó
ô
ô
õ
ó 4t 3 dt
ó tdt
ó dt
t +1-1
dt
ó
ó
=
= 4ô
= 4ô
dt
= 4ô
- 4ô
=
ô 2
10
10
10
10
9
10
õ (t + 1)
õ t (t + 1)
õ (t + 1)
x 4 x +1
õ (t + 1)
õ (t + 1)
(
dx
)
= 4 ò (t + 1) d (t + 1)- 4 ò (t + 1)
-9
-10
d (t + 1) = -
1
2(t + 1)
8
ПОДСТАНОВКИ ЭЙЛЕРА
ò R (x, ax + bx + c )dx
2
+
4
9(t + 1)
I =-
ax 2 + bx + c = ± a x + t
(
+C
1
+
4
) 9(4 x + 1)
2 4 x +1
8
9
+ C.
a¹0
3) ax 2 + bx + c = a (x - a )(x - b )
2) с > 0
1) a > 0
9
ax 2 + bx + c = xt ± c
ax 2 + bx + c = (x - a )t
интеграл от рациональной функции переменной t
8/20

9.

ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
(
)
R
sin
x
,
cos
x
dx
ò
рациональная функция
x
2 tg
2t
2
sin x =
=
2
2 x
1
+
t
1 + tg
2
2 x
1 - tg
2
1
t
2 =
cos x =
2
2 x
1
+
t
1 + tg
2
ó dx
ô
õ sin x
универсальная
тригонометрическая
подстановка
x = 2 arctg t
x
t = tg
2
Интеграл от рациональной
функции аргумента t
2dt
1+ t 2
ó 2dt
ô 1+ t2
=ô
2t
ô
õ 1+ t2
( x ¹ p + 2pk , k Î z )
-p < x < p
ó æ 2t 1 - t 2 ö 2dt
÷
,
ô Rçç
2
2÷
2
1
+
t
1
+
t
1
+
t
õ è
ø
x
= arctg t
2
dx =
x
tg = t
2
dx
ó
ô
õ 4 + 5 sin x + 3 cos x
x
dt
ó
= ln t + C = ln tg + C
=ô
2
õ t
9/20

10.

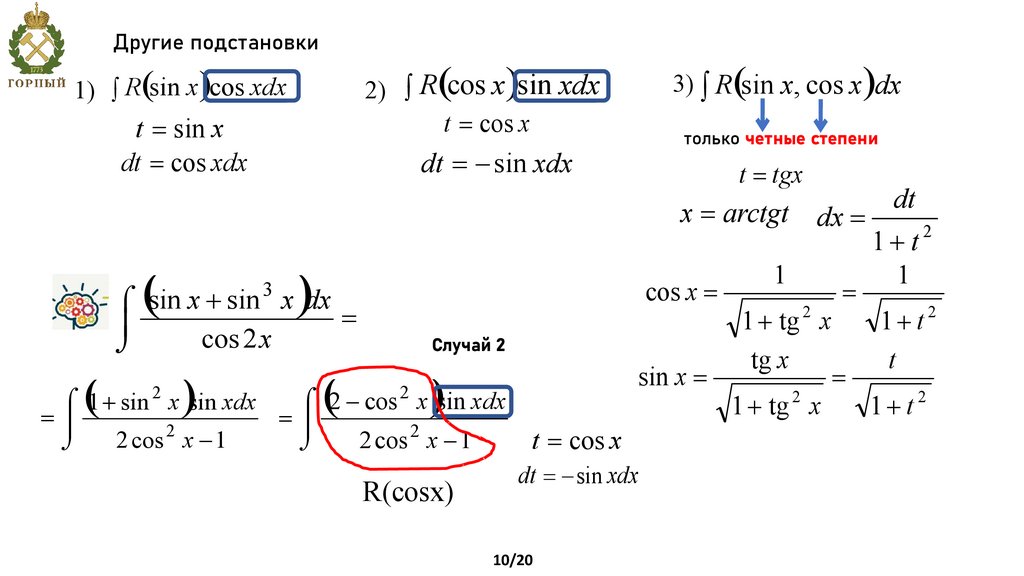
Другие подстановки
2) ò R (cos x )sin xdx
t = cos x
1) ò R (sin x )cos xdx
t = sin x
dt = cos xdx
(
3
)
только четные степени
dt = - sin xdx
t = tgx
dt
x = arctgt dx =
2
1+ t
)
ó sin x + sin x dx
=
ô
cos 2 x
õ
(
3) ò R(sin x, cos x )dx
(
cos x =
Случай 2
sin x =
)
ó 2 - cos 2 x sin xdx
ó 1 + sin 2 x sin xdx
=ô
=ô
2
2
2
cos
x
1
2 cos x - 1
õ
õ
R(cosx)
t = cos x
dt = - sin xdx
10/20
1
2
1 + tg x
tg x
1 + tg 2 x
=
=
1
1+ t
t
1+ t2
2

11.

ó
dx
ó
ô
ô
=
2
2
õ sin x + 2 sin x cos x - cos x ô
õ
dx
d (tgx )
ó
cos 2 x
=ô 2
2
õ tg x + 2tgx - 1
tg x + 2tgx - 1
Интегралы вида:
sinmx cosnx dx,
sinmx sinnx dx,
cosmx cosnx dx, m ≠ n
sin α cos β =
sin α sin β =
1
1
= [sin (α - β)+ sin (α + β)] = [cos(α - β )- cos(α + β )]
2
2
cos α cos β =
1
= [cos(α - β )+ cos(α + β )]
2
1
1
1
=
sin
2
x
+
sin
8
x
+
C
cos
3
x
cos
5
xdx
=
(
)
cos
2
x
+
cos
8
x
dx
ò
ò
4
16
2
11/20

12.

Интегралы вида sinmx cosnx dx,
1)хотя бы одна из степеней m или n нечетная положительная
Пусть n = 2k + 1.
Остальные множители выражаем через sin x
(основное тригонометрическое тождество)
Отделить cos x и подвести под
знак дифференциала.
m
2 k +1
m
2k
m
2
k
sin
x
cos
xdx
=
sin
x
cos
x
cos
xdx
=
sin
x
(cos
x
)
d sin x =
ò
ò
ò
= ò sin x(1 - sin x ) d sin x
m
2
k
2) оба числа m и n четные неотрицательные
ò
1
ó æ 1 - cos 2 x ö
2
dx
÷ =
sin xdx =ô ç
2
õè
ø
2
формулы
ò dx -ò cos 2 xdx = понижения
степени:
(
)
x sin 2 x
= +C
2
4
12|20
1 + cos 2 x
cos x =
2
1 - cos 2 x
2
sin x =
2
2
sin 2 x
sin x cos x =
2

13.

,
sinmx cosnx dx
;.
3) числа m и n отрицательные одинаковой четности:
2
cos x и подвести под дифференциал.
В знаменателе отделить
Остальные функции выразить через tgx по формулам:
tg x
1
2
2
sin x =
; cos x =
.
2
1 + tg x
1 + tg 2 x
ó dx = ó
dx
ì dx
ü ó d tg x
= d ( tg x) ý = ô
= í
=
ô
ô
2
2
2
4
þ õ cos 2 x
õ cos x õ cos x cos x î cos x
(
2
)
= ò 1 + tg x d (tg x) =
tg 3 x
tg x +
+C
3
13|20

14.

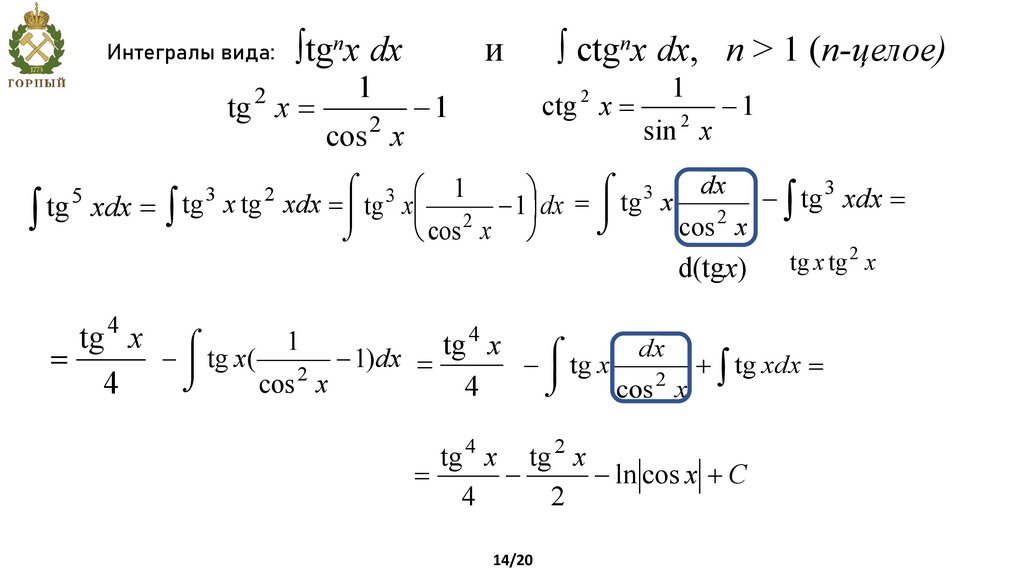
Интегралы вида:
2
tgnx dx
tg x =
ò
1
2
cos x
и
ctgnx dx, n > 1 (n-целое)
1
ctg x =
-1
2
sin x
2
-1
ó 3 æ 1
ö = ó tg 3 x dx - tg 3 xdx =
tg xdx = ò tg x tg xdx =ô tg xç 2 - 1÷ dx ô
ò
2
õ
cos x
õ
è cos x ø
3
5
2
d(tgx)
4
tg x tg 2 x
4
tg x ó
1
tg
x
dx
ó
- ô tg x(
1
)
dx
=
=
- ô tg x
+ ò tg xdx =
2
2
õ
cos x
4
õ
4
cos x
tg 4 x tg 2 x
=
- ln cos x + C
4
2
14/20

15.

ЧАСТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ПОДСТАНОВКИ
;
если R(sin x,cos x) нечетная функция относительно sin x,
т.е. R( sin x,cos x) = –R(sin x,cos x), то применяется подстановка
t = cos x;
если R(sin x, cos x) – нечетная функция относительно cos x,
т.е. R(sin x, cos x) = –R(sin x, cos x), то применяется подстановка
t = sin x;
если R(sin x, cos x) – четная функция относительно sin x и cos x,
т.е. если R( sin x,
подстановка
cos x) = R(sinx,
t = tgx.
15|20
cosx),
то
применяется

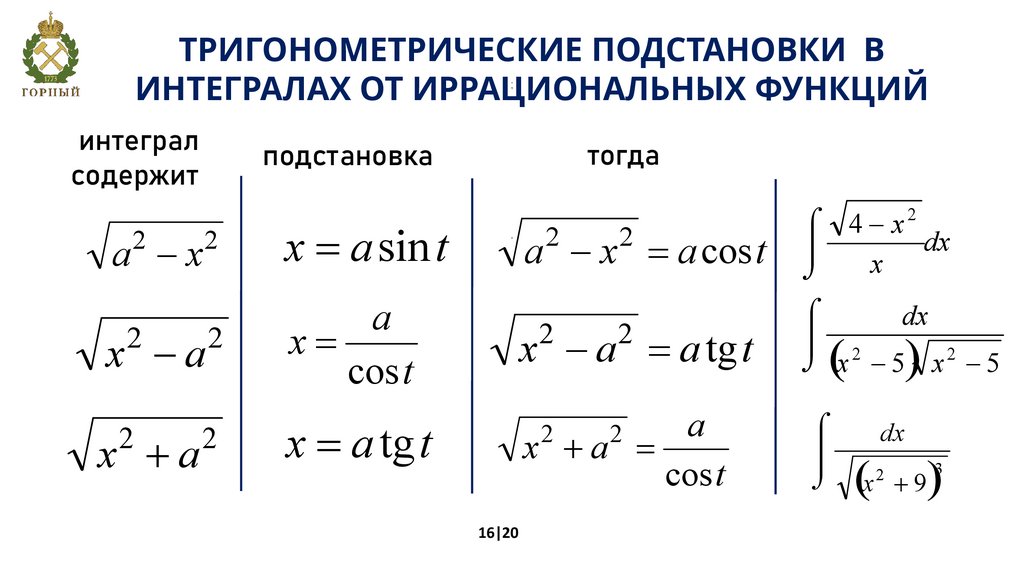
16.

ТРИГОНОМЕТРИЧЕСКИЕ ПОДСТАНОВКИ В
ИНТЕГРАЛАХ ОТ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
;
интеграл
содержит
2
a -x
2
x +a
2
2
a - x = a cos t
ó 4-x
dx
ô
x
õ
2
2
2
x = a sin t
2
a
x=
cos t
x - a = a tg t
ó
dx
ô 2
õ x - 5 x2 - 5
x = a tg t
a
x +a =
cos t
ó
ô
ô
õ
x -a
2
тогда
подстановка
2
.
2
2
16|20
2
(
)
dx
(x + 9)
2
3

17.

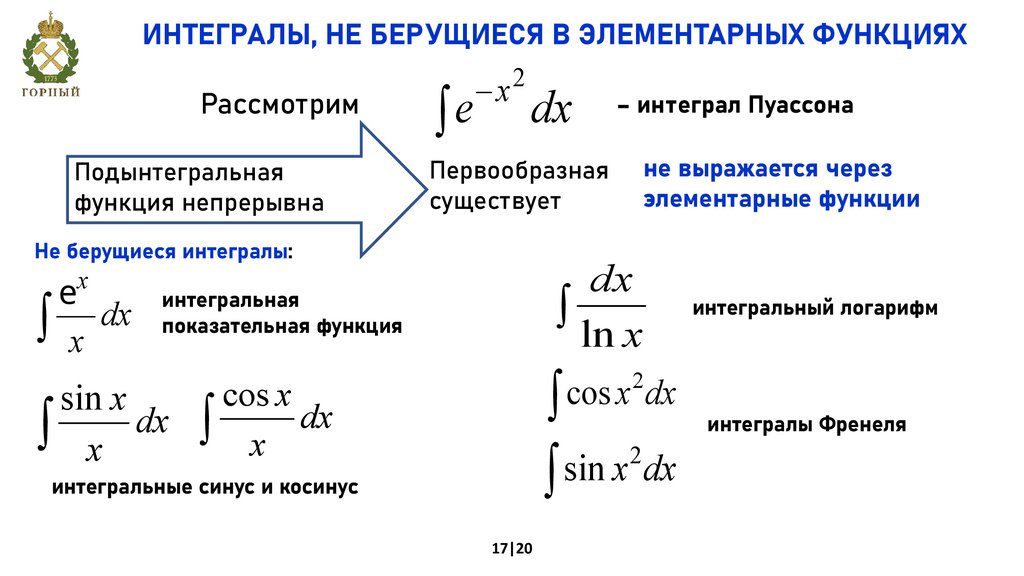
ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
Рассмотрим
Подынтегральная
функция непрерывна
òe
-x
2
dx
не выражается через
элементарные функции
Первообразная
существует
Не берущиеся интегралы:
dx
ò ln x
x
e
интегральная
ò x dx показательная функция
sin x
dx
ò x
– интеграл Пуассона
cos
x
dx
ò
интегральный логарифм
2
cos x
ò x dx
sin
x
dx
ò
2
интегральные синус и косинус
17|20
интегралы Френеля

18.

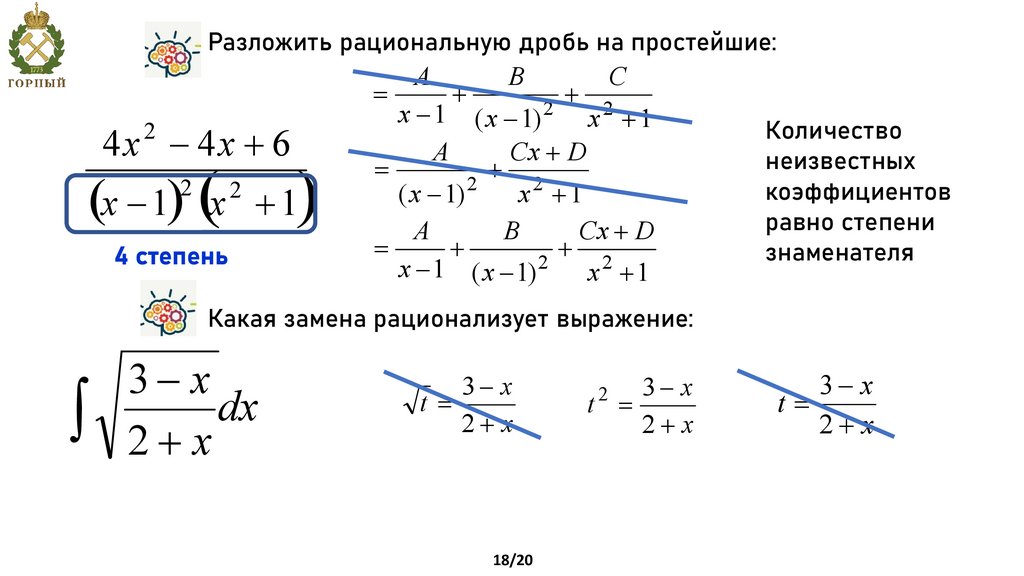
Разложить рациональную дробь на простейшие:
2
4x - 4x + 6
(x - 1) (x + 1)
2
2
4 степень
A
B
С
=
+
+ 2
2
x - 1 ( x - 1)
x +1
А
Cx + D
=
+ 2
2
( x - 1)
x +1
A
B
Cx + D
=
+
+
x - 1 ( x - 1) 2 x 2 + 1
Количество
неизвестных
коэффициентов
равно степени
знаменателя
Какая замена рационализует выражение:
ò
3- x
dx
2+ x
3- x
t =
2+ x
18/20
3- x
t =
2+ x
2
3- x
t=
2+ x

19.

Какая замена в интеграле удобна, чтобы свести
его к интегралу от рациональной функции?
t = cos x
t = sin x
cos xdx
ò (sin х) 2025
t = tg x
Какую замену нужно сделать в интеграле
dx
ò ( x - 16) x - 16
2
чтобы свести его к интегралу от тригонометрической функции?
x=2sin t
x=4sin t
x=4 / cos t
19/20
x=cos 4 t
2

20.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
20/20