Похожие презентации:
Рекурсия: запутанная история
1. Рекурсия: Запутанная история
2.
История развития ДМ. ЗадачиПринцип Дирихле
Основные правила комбинаторики
Выборки. Комбинаторные числа
Метод включений и исключений
Бином Ньютона. Полиномиальная формула
Рекуррентные соотношения
Производящие функции
3.
ЛИНЕЙНЫЕ ОДНОРОДНЫЕРЕКУРРЕНТНЫЕ
СООТНОШЕНИЯ С
ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
4.
5.
Существует общий метод для решения линейныхрекуррентных
соотношений
с
постоянными
коэффициентами, т.е. для рекуррентных соотношений вида:
f(n + k) = a1 ∙ f(n + k – 1) + a2 ∙ f(n + k – 2) + … + ak ∙ f(n),
где a1, a2, …, ak — постоянные коэффициенты.
6.
Рассмотрим этот метод для линейных рекуррентныхсоотношений с постоянными коэффициентами второго
порядка, т.е. при k = 2;
рекуррентное соотношение при этом имеет вид:
f(n + 2) = a1 ∙ f(n + 1) + a2 ∙ f(n).
7.
Теорема. Пусть дано рекуррентное соотношениеf(n + 2) = a1 ∙ f(n + 1) + a2 ∙ f(n).
Составим характеристическое уравнение (квадратное)
t2 = a1∙t + a2
Если это уравнение имеет два различных корня t1 и t2, то
общее решение имеет вид
n 1
n 1
f (n) c1 t 1 c 2 t 2
8.
Пример. Найти общее решение рекуррентного соотношенияf(n + 2) = 15f(n + 1) – 56f(n).
Решение
Соответствующее
квадратное
уравнение
имеет
вид
t2 = 15t – 56.
Это уравнение имеет два различных корня t1 = 7 и t2 = 8,
общее решение этого рекуррентного соотношения имеет вид
f (n) c1 7
n 1
n 1
c2 8
9.
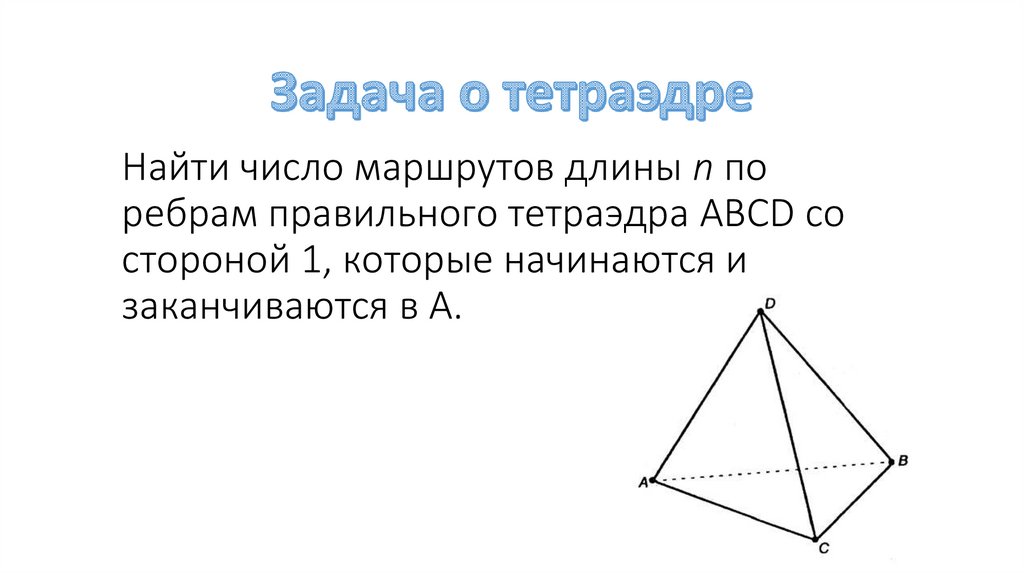
Найти число маршрутов длины n поребрам правильного тетраэдра ABCD со
стороной 1, которые начинаются и
заканчиваются в А.
10. Обозначим аn – число замкнутых маршрутов длины n из А в А, bn - число маршрутов из А в В, сn - из А в С, dn - из А в D.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
Линейныерекуррентные
соотношения
с
постоянными
коэффициентами более высокого порядка решаются аналогично.
Если рекуррентное соотношение имеет вид
f(n + k) = a1 ∙ f(n + k – 1) + a2 ∙ f(n + k – 2) + … + ak ∙ f(n),
где a1, a2, …, ak — постоянные коэффициенты, то уравнение
t a1 t
k
k 1
a2 t
k 2
... a k
называется характеристическим уравнением этого
рекуррентного соотношения.
23.
24.
Пример. Найти общее решение рекуррентногосоотношения
f(n + 4) = 5f(n + 3) – 6f(n + 2) – 4f(n + 1) + 8f(n).
Решение
Соответствующее характеристическое уравнение
имеет вид
t4 – 5t3 + 6t2 + 4t – 8 = 0.
Оно имеет корни t1 = t2 = t3 = 2; t4 = –1,
общее решение этого рекуррентного соотношения
имеет вид:
f(n) = (c1 + c2 ∙ n + c3 ∙ n2) 2n – 1 + c4(–1)n – 1.
25. Если характеристическое уравнение имеет два комплексных корня z1 и z2, то они будут комплексно-сопряженными, т.е. z1=a+ib,
z2=a-ib.Общее решение
26.
27.
28.
29.
30.
31.
32.
33. Пример
34.
35.
36.
ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ РЕКУРРЕНТНЫЕСООТНОШЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ЛНРСПК содержат в правой части дополнительное слагаемое d(n):
f(n + k) = a1 ∙ f(n + k – 1) + a2 ∙ f(n + k – 2) + … + ak ∙ f(n) + d(n).
37.
Решение таких РС представляют ввиде
суммы
общего
решения
соответствующего однородного РС и
какого-либо
частного
решения
неоднородного РС.
f(n) = f(n)оо + f(n)чн
38.
На практике часто встречается случай, когдаd(n) имеет вид:
d(n) = Pm(n)*tn,
где Pm(n) – полином степени m,
t – константа.
Частное решение в этом случае следует искать
в виде:
f(n)чн = ns*Qm(n)* tn,
где Qm(n) – некоторый полином степени m,
s – кратность корня t.



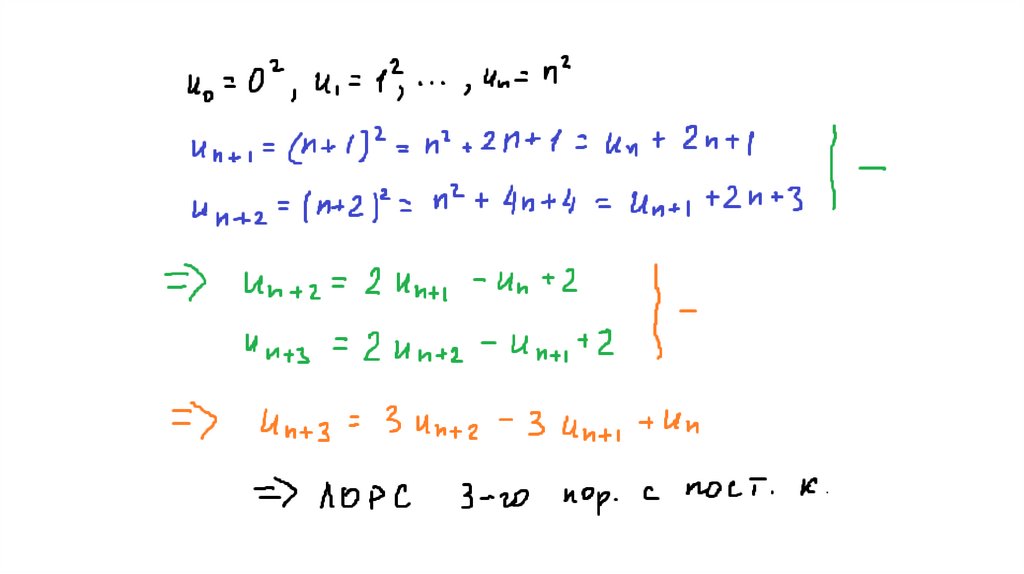





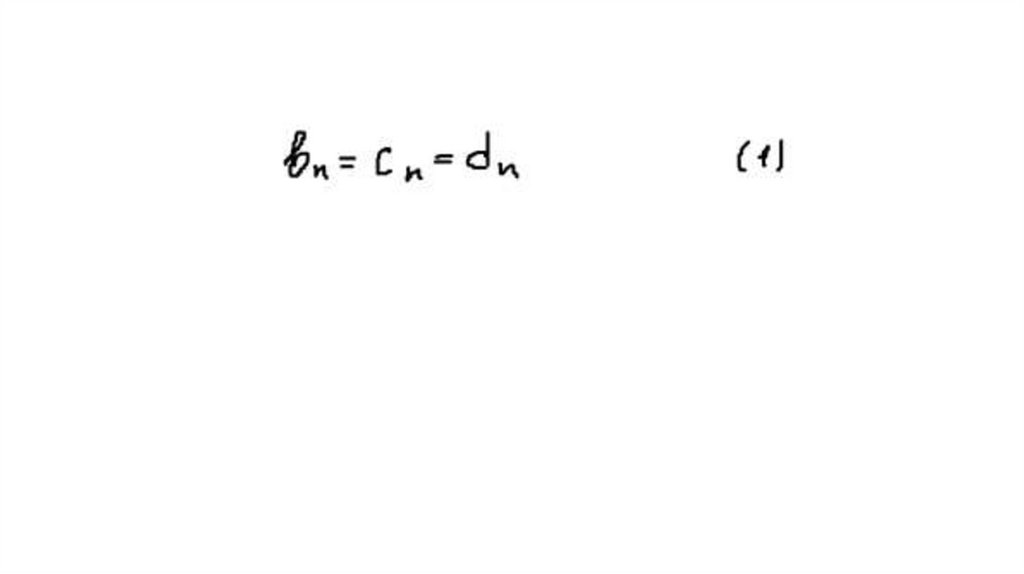
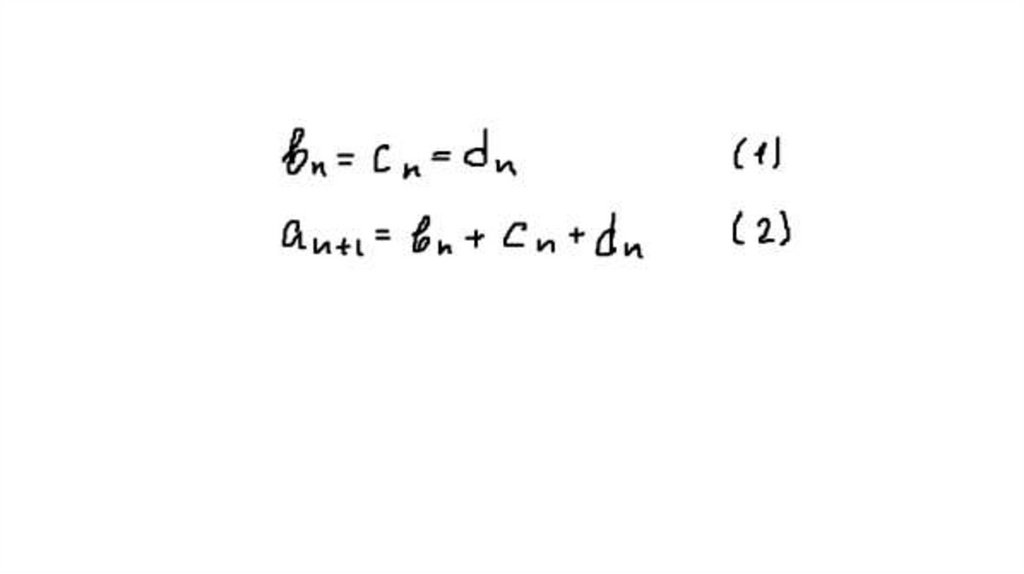
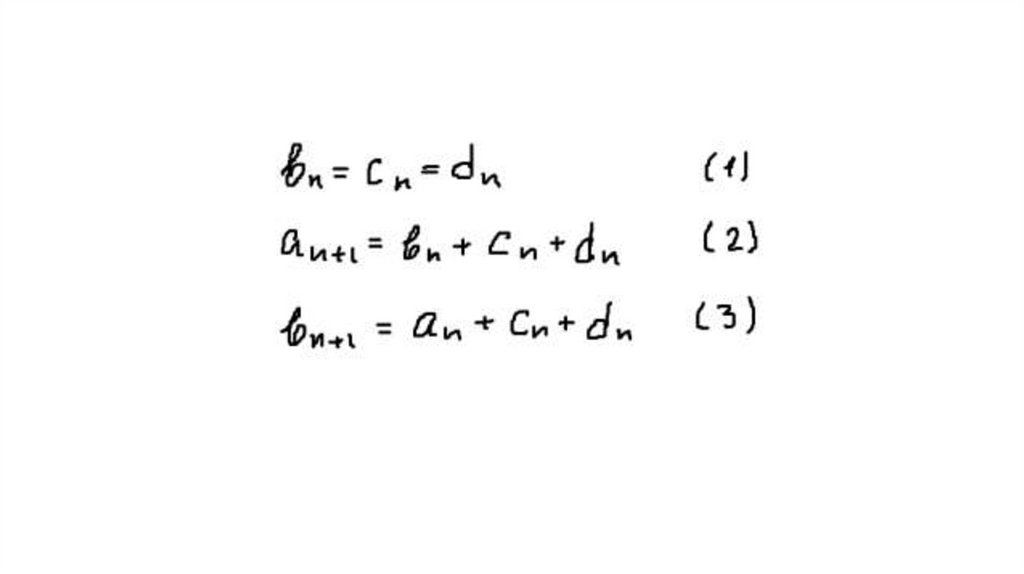
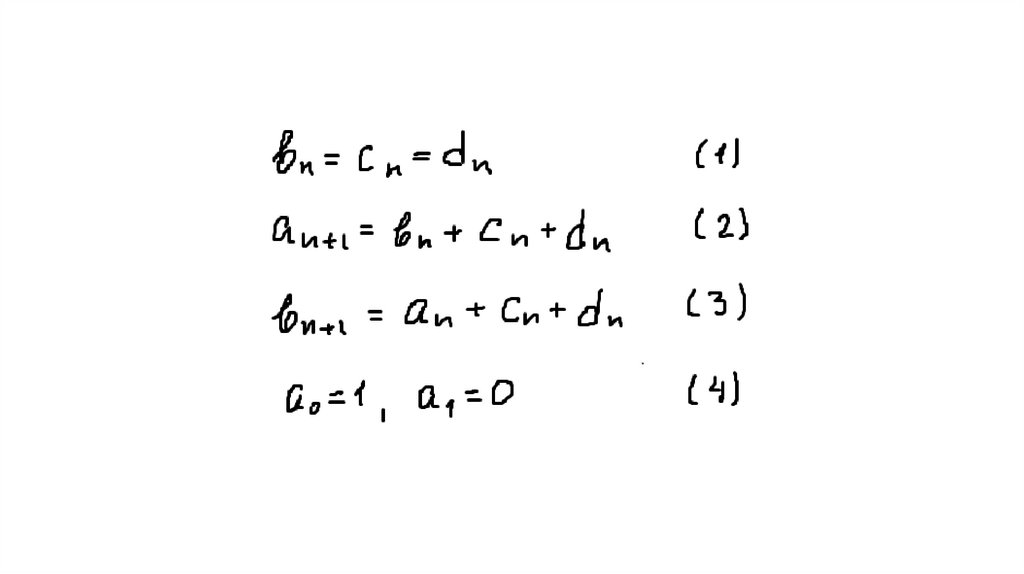
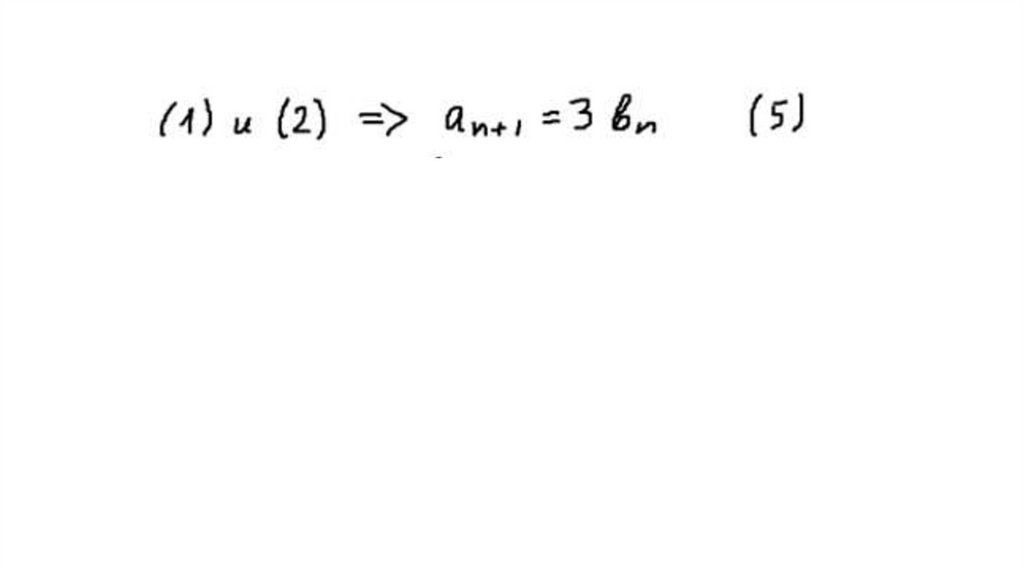
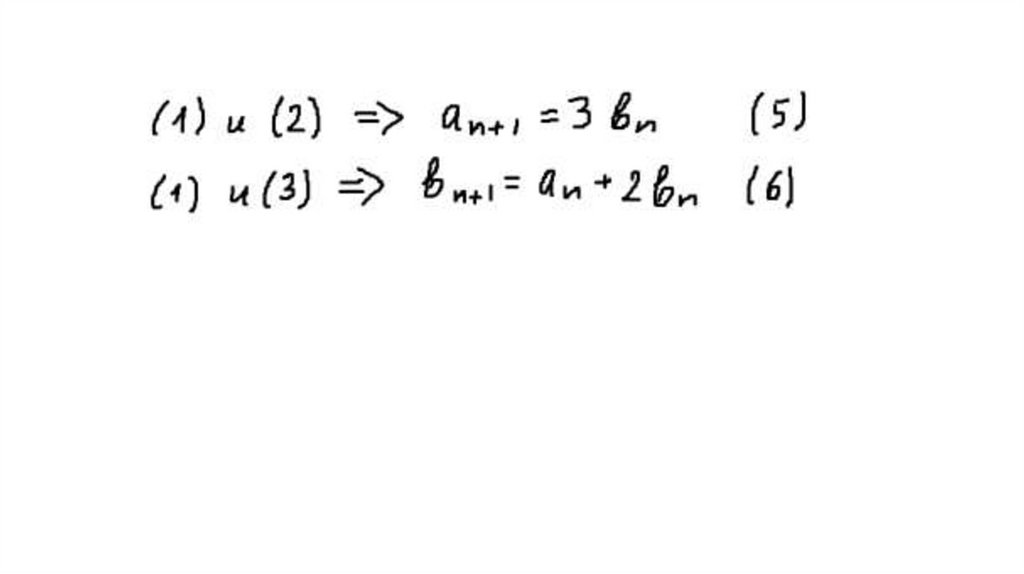
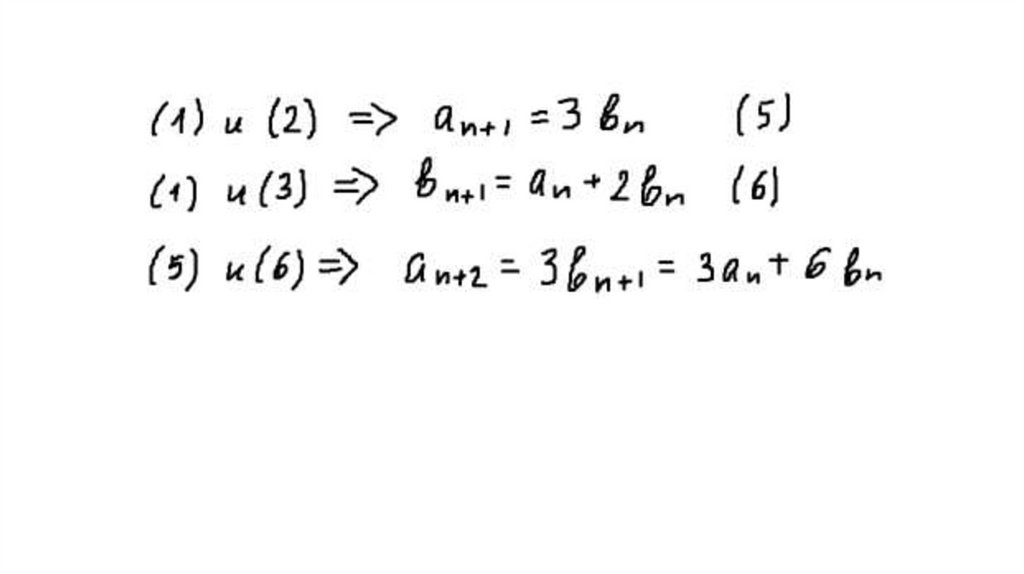
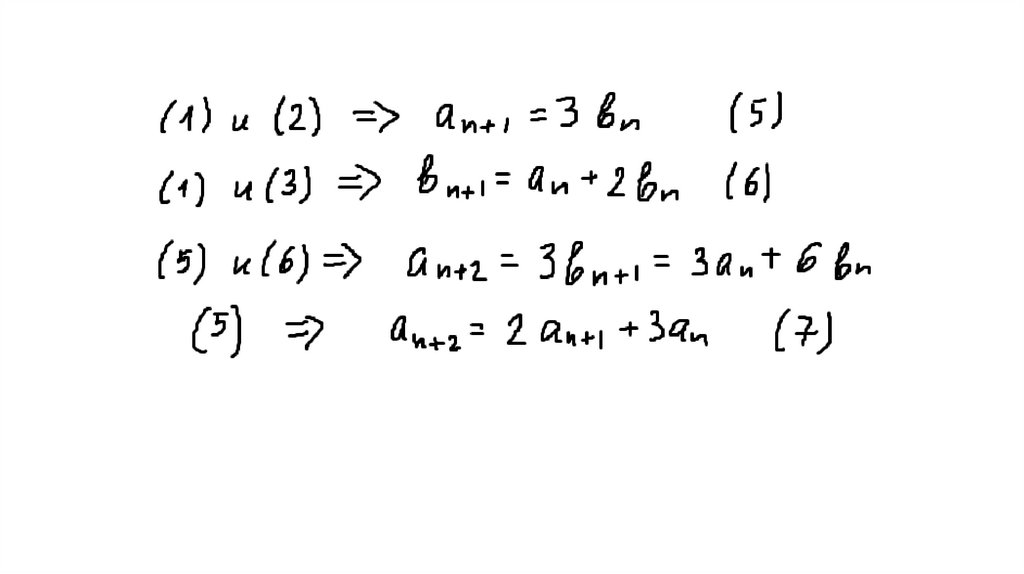








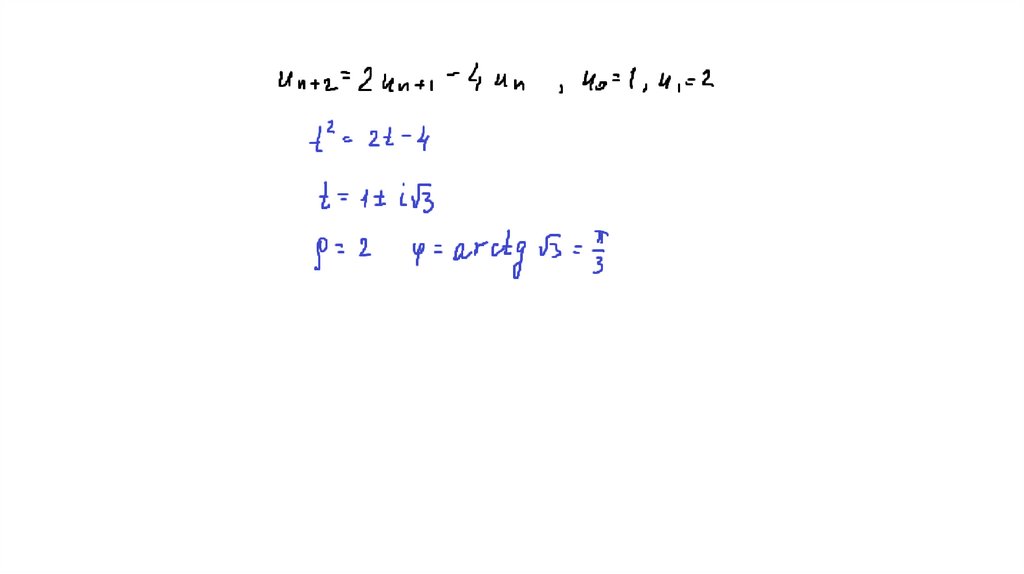
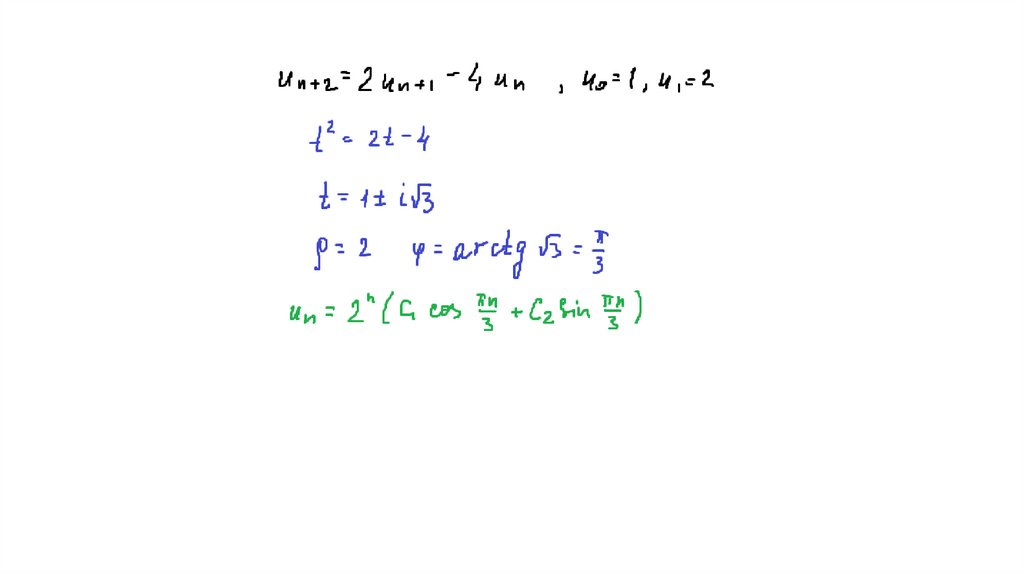
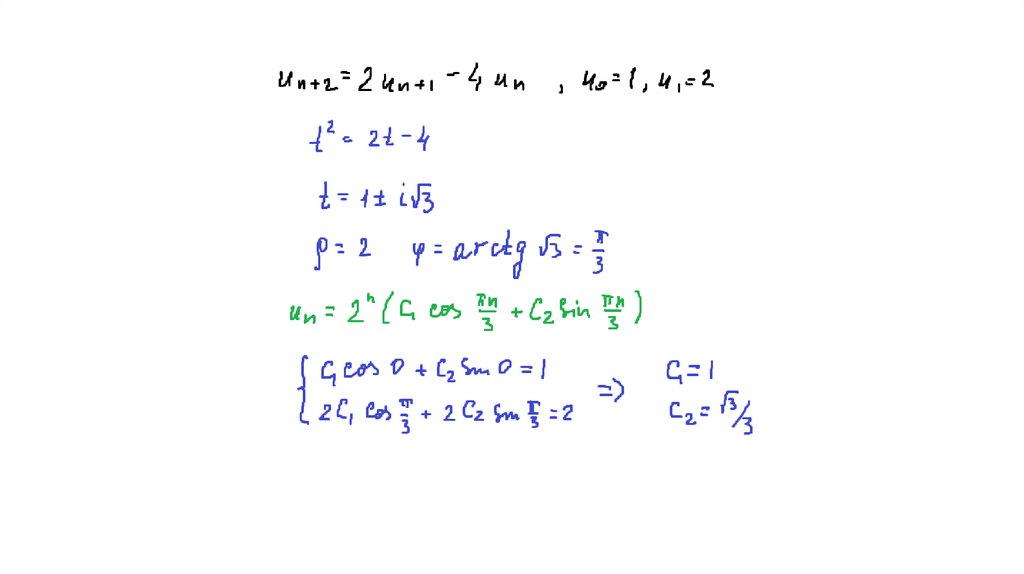
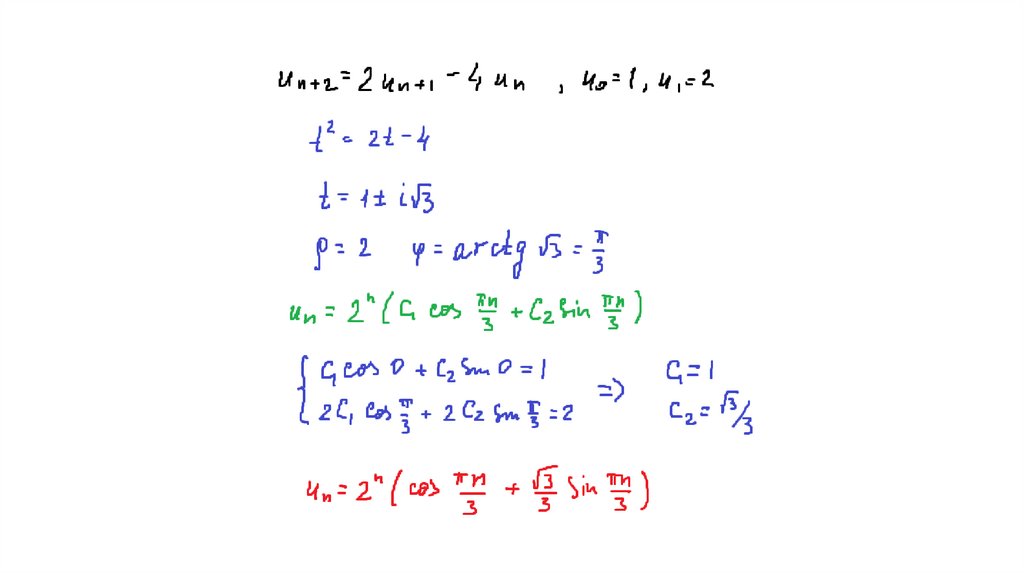
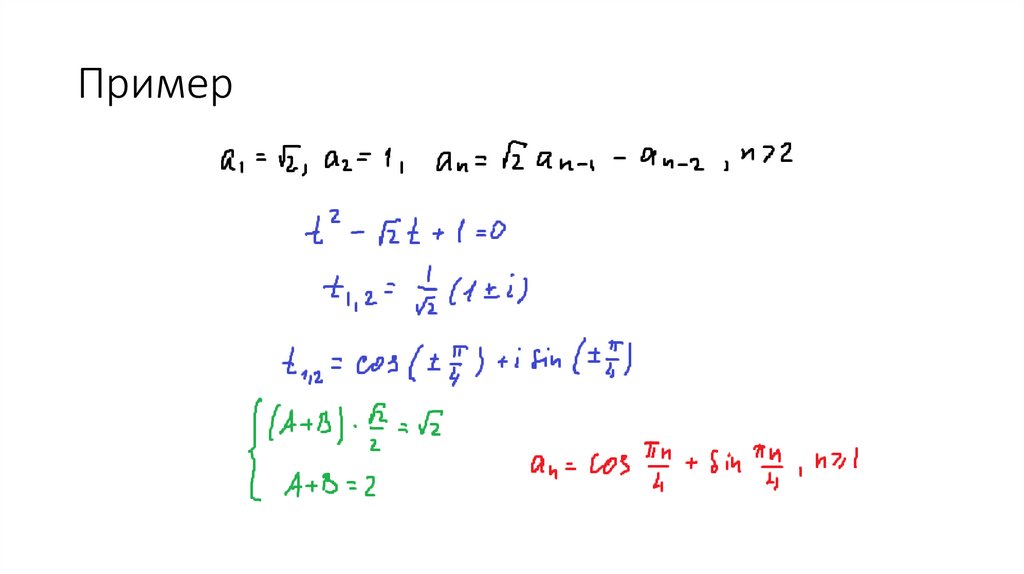



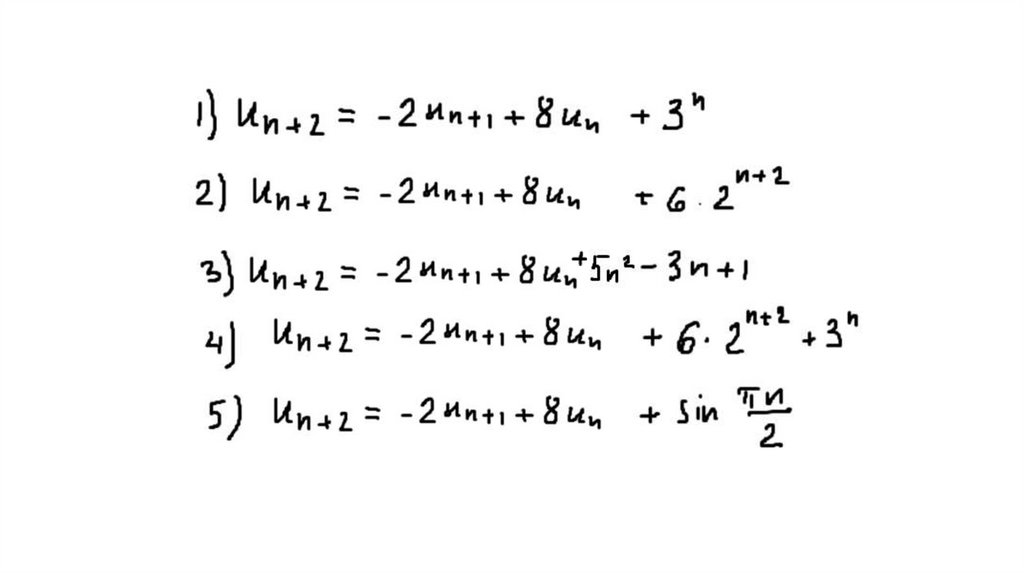
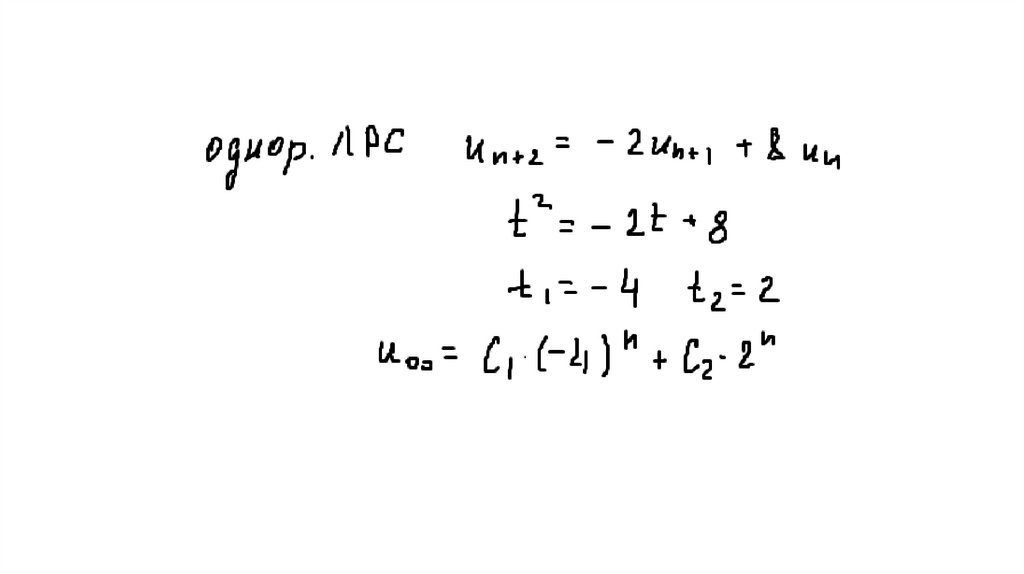
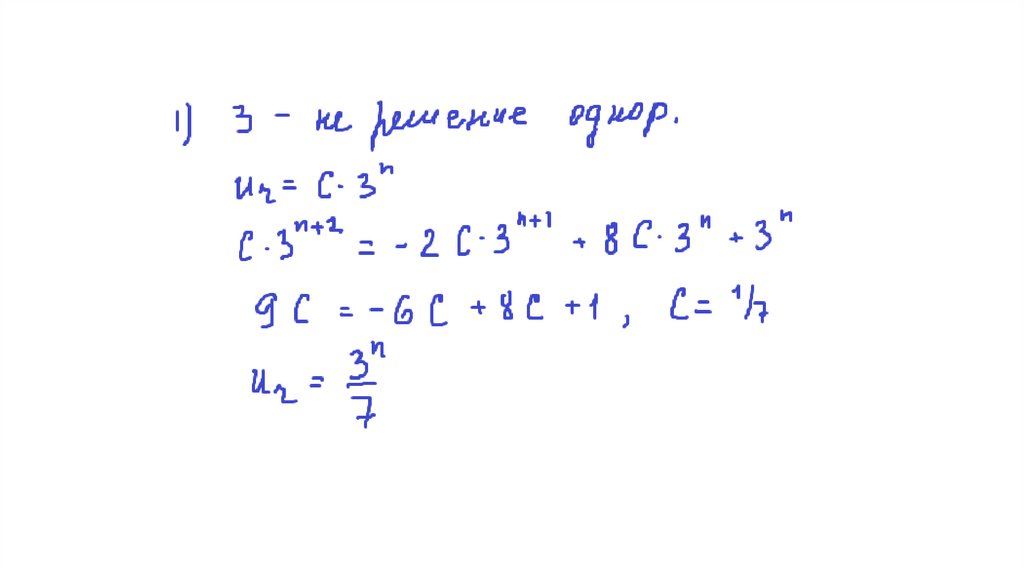
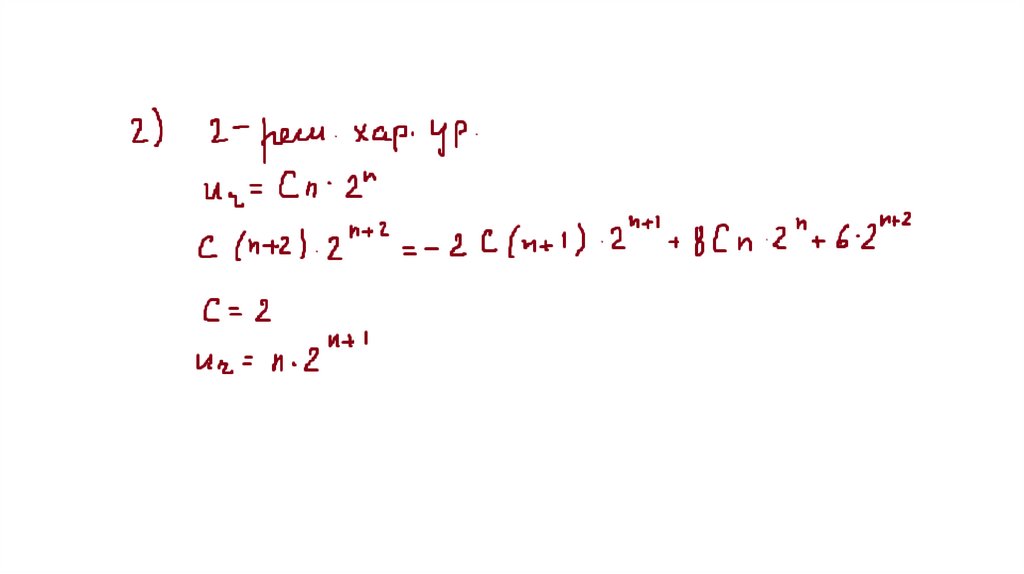
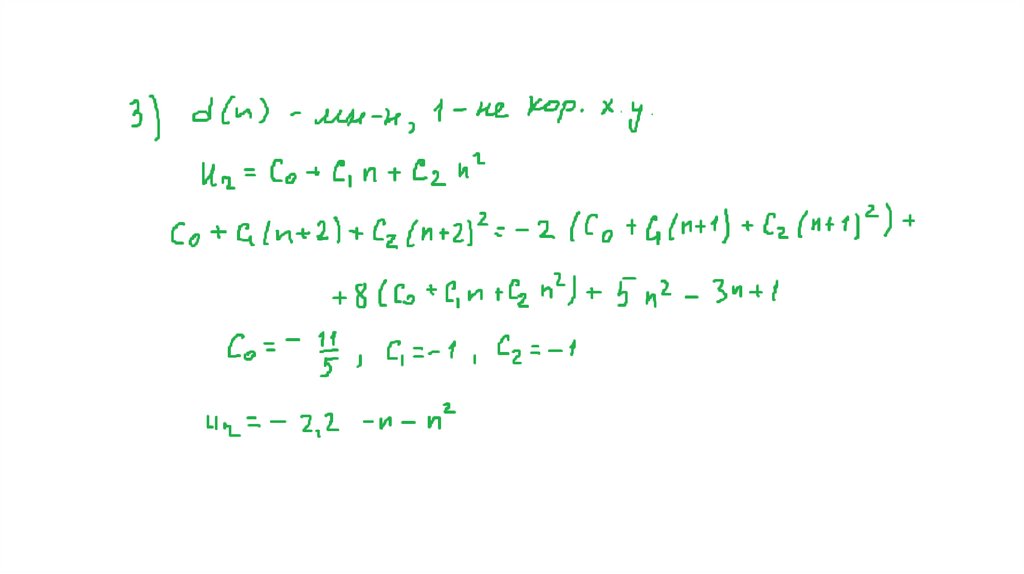
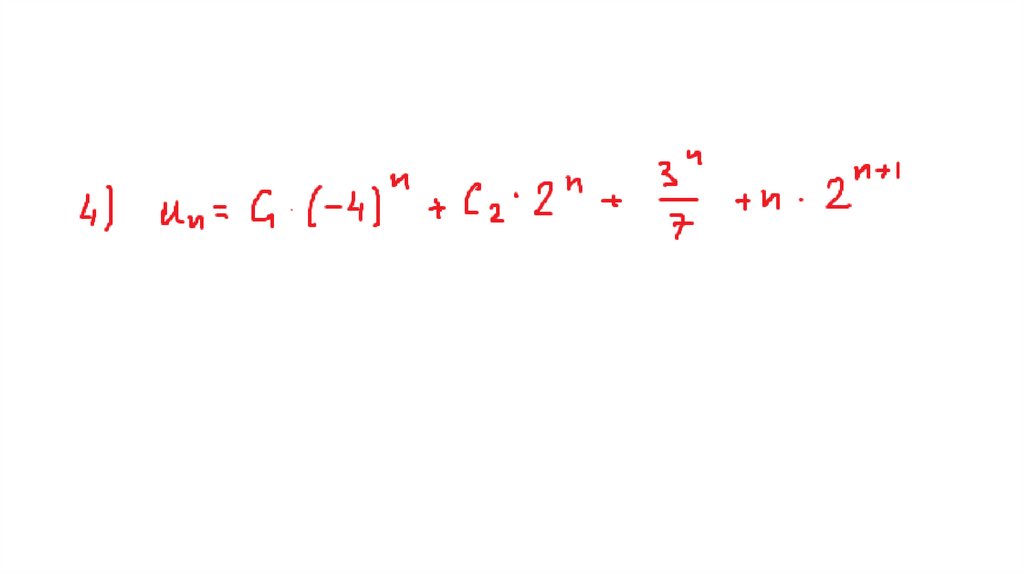
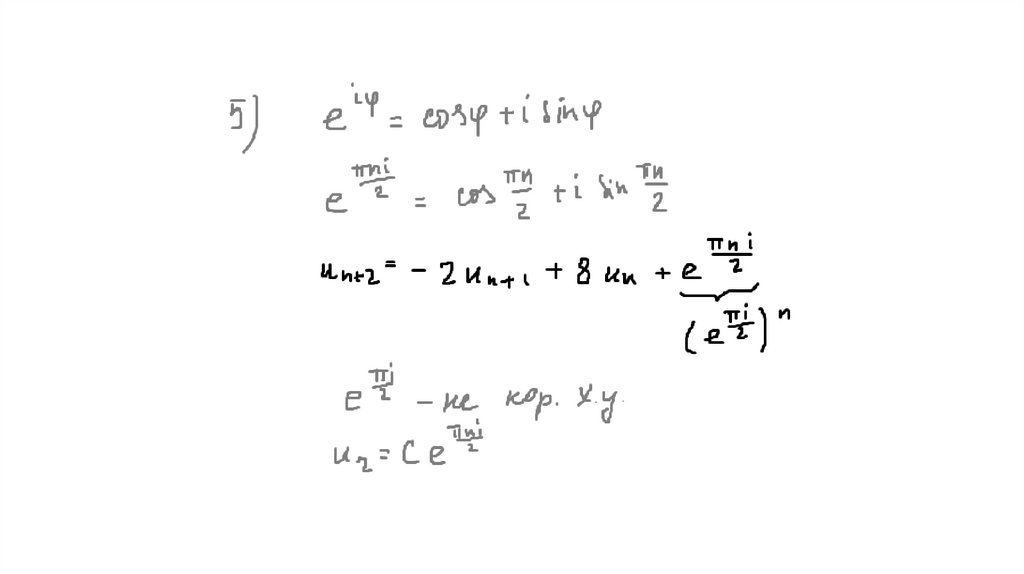
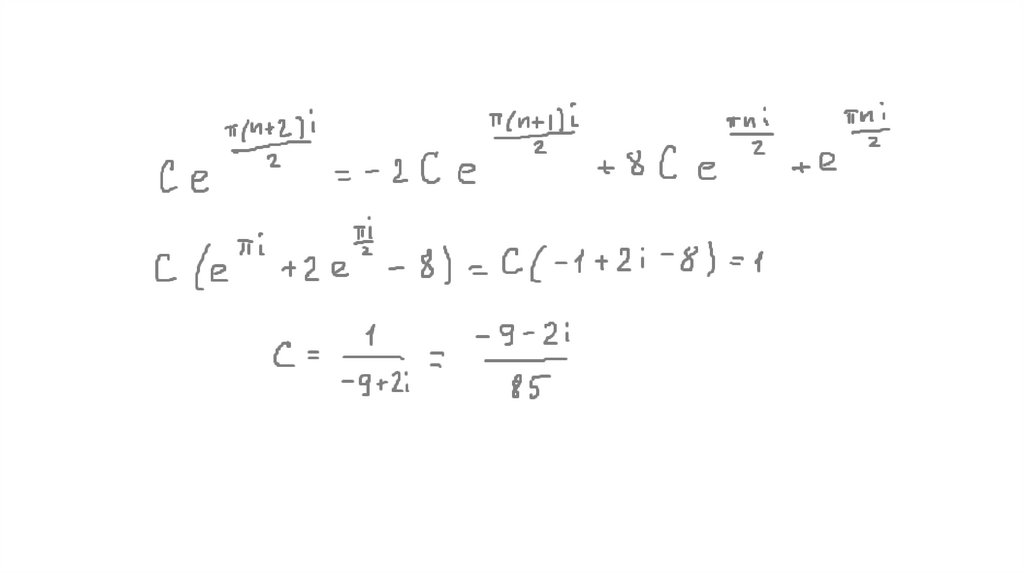
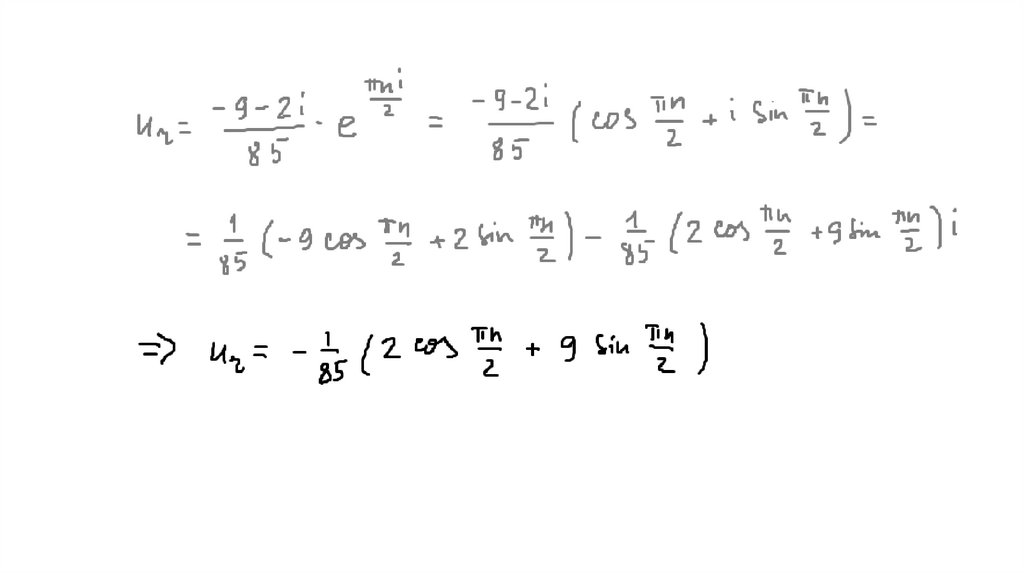


 Математика
Математика








