Расчёт изгибаемых элементов деревянных конструкций

1. ЛЕКЦИЯ РАСЧЁТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХ КОНСТРУКЦИЙ

ПЕРЕЧЕНЬ РАССМАТРИВАЕМЫХ ВОПРОСОВ:
1. Общие положения
2. Проверка изгибаемых элементов деревянных конструкций
предельным состояниям несущей способности
3. Проверка изгибаемых элементов деревянных конструкций
предельным состояниям эксплуатационной пригодности
по
по

2. 1 Общие положения

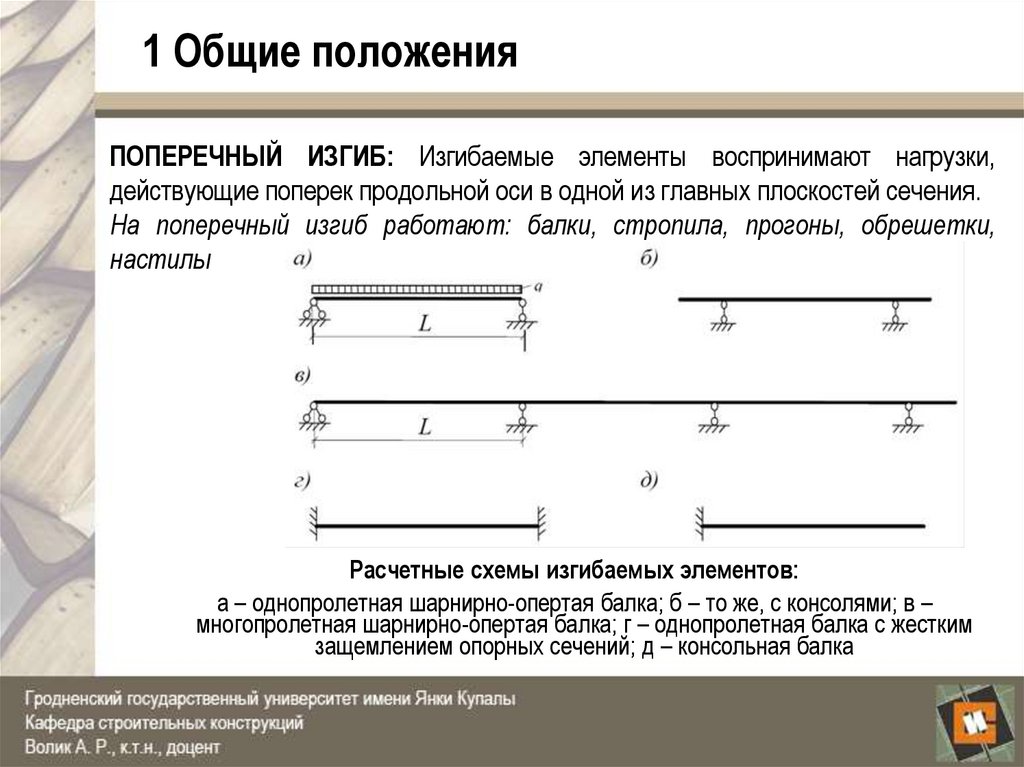
ПОПЕРЕЧНЫЙ ИЗГИБ: Изгибаемые элементы воспринимают нагрузки,
действующие поперек продольной оси в одной из главных плоскостей сечения.
На поперечный изгиб работают: балки, стропила, прогоны, обрешетки,
настилы
Расчетные схемы изгибаемых элементов:
а – однопролетная шарнирно-опертая балка; б – то же, с консолями; в –
многопролетная шарнирно-опертая балка; г – однопролетная балка с жестким
защемлением опорных сечений; д – консольная балка

3. 1 Общие положения

В
изгибаемых
элементах
от
нагрузок, действующих поперек
продольной
оси,
возникают
изгибающий
момент
МEd
и
поперечная сила Ved, определяемые
методами строительной механики.
MEd=qdleff2/8
VEd=qdleff/2.

4. 1 Общие положения

5. ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ

а)
б)
m
80
, МПа
40
h
c.o.
0
20
40
U,мм
t.o.
b
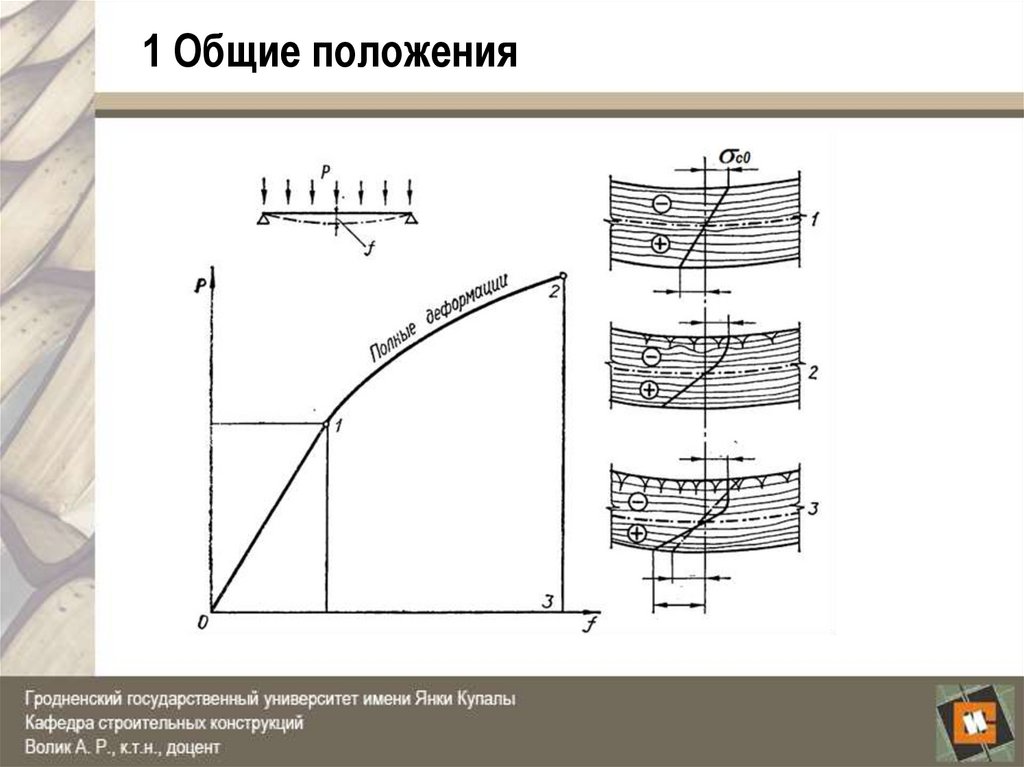
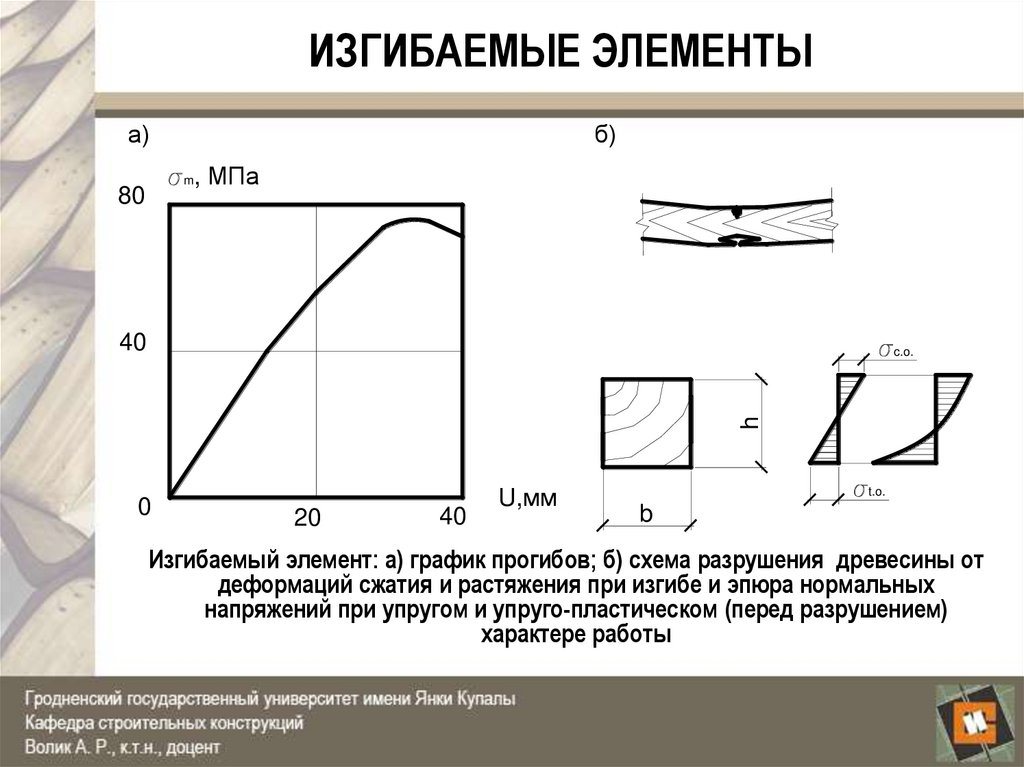
Изгибаемый элемент: а) график прогибов; б) схема разрушения древесины от
деформаций сжатия и растяжения при изгибе и эпюра нормальных
напряжений при упругом и упруго-пластическом (перед разрушением)
характере работы

6. ПРОВЕРКА ПРЕДЕЛЬНЫХ СОСТОЯНИЙ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ

Несущей
способности
Эксплуатационной
пригодности
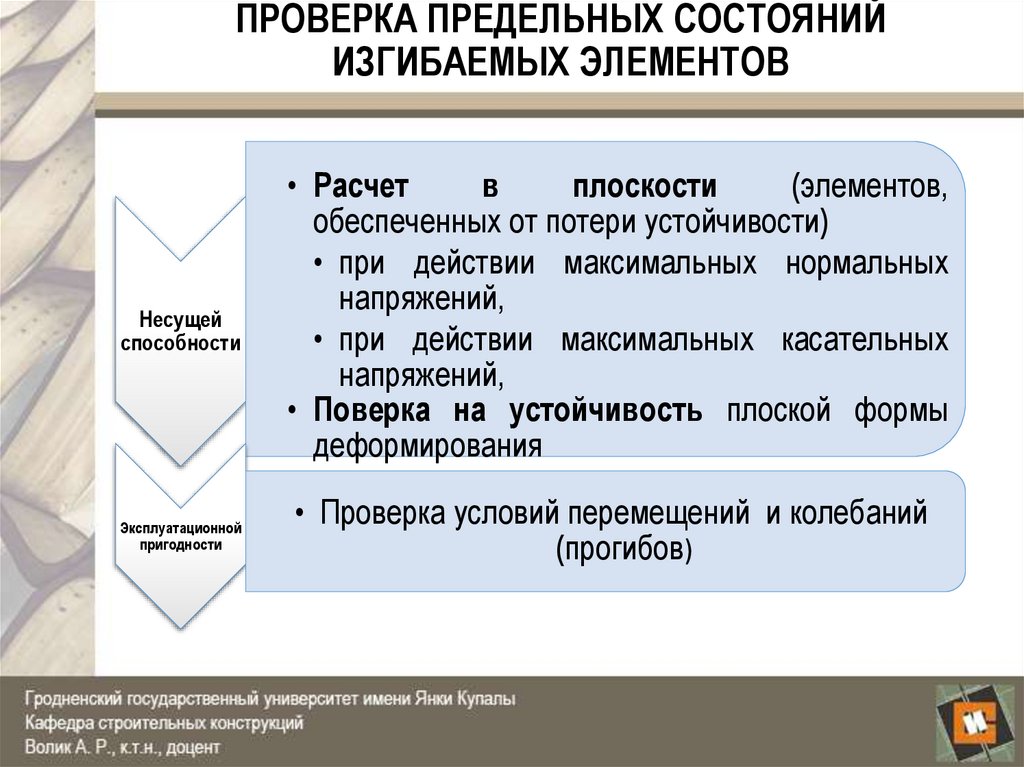
• Расчет
в
плоскости
(элементов,
обеспеченных от потери устойчивости)
• при действии максимальных нормальных
напряжений,
• при действии максимальных касательных
напряжений,
• Поверка на устойчивость плоской формы
деформирования
• Проверка условий перемещений и колебаний
(прогибов)

7. 2. ПРОВЕРКА ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ НЕСУЩЕЙ СПОСОБНОСТИ

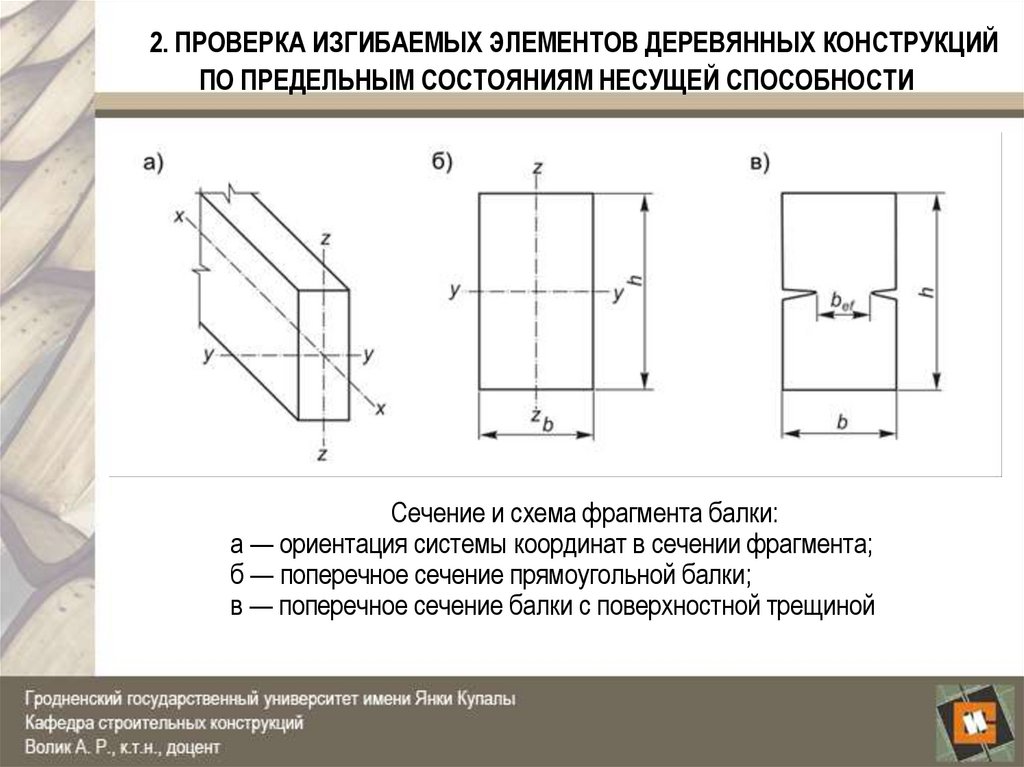
Сечение и схема фрагмента балки:
а — ориентация системы координат в сечении фрагмента;
б — поперечное сечение прямоугольной балки;
в — поперечное сечение балки с поверхностной трещиной

8. 2. ПРОВЕРКА ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ НЕСУЩЕЙ СПОСОБНОСТИ

При проверке элементов постоянного сплошного поперечного сечения,
подверженных изгибу только в одной плоскости (изгиб только относительно
оси у или z), и когда исключена потеря устойчивости плоской формы
деформирования (приведенная гибкость элемента при изгибе λrel,m 0,75,
должны соблюдаться условия:
My,Ed My,Rd или Mz,Ed Mz,Rd
VEd VRd
My,Ed и Mz,Ed — расчетные значения изгибающего момента в сечении
элемента, обусловленного внешними воздействиями;
My,Rd и Mz,Rd — расчетные значения сопротивления в нормальном сечении
элемента;
VEd – расчетное значение сдвигающего усилия в сечении изгибаемого
элемента, обусловленного внешним воздействием;
VRd — расчетное значение сопротивления сдвигу в сечении изгибаемого
элемента.

9. 2. ПРОВЕРКА ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ НЕСУЩЕЙ СПОСОБНОСТИ

относительно осей у
относительно осей z
M y,Rd f m,y,dWy,d
M z,Rd f m,z,dWz,d
расчетные значения прочности древесины при изгибе
f m,y ,d
kmod ksys kh f m,k
m
f m,z,d
kmod ksys kb f m,k
m
момент сопротивления:
Wy , d
bh
6
2
hb 2
Wz ,d
6
Для элементов сплошного поперечного сечения, имеющих ослабления W d = Wnet .
При определении Wnet ослабления сечений, расположенные на участке элемента
длиной не более 200 мм, принимают совмещенными в одном сечении.

10. РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ НА СДВИГ

Расчетное значение сопротивления сдвигу в сечении изгибаемого элемента
VRd Sbr
d
I br bef
VRd
I br bef fv ,d
Sbr
Sbr - статический момент брутто сдвигаемой части поперечного сечения
элемента относительно нейтральной оси;
I br - момент инерции брутто поперечного сечения элемента относительно
нейтральной оси;
bef kcr bрасчетная ширина сечения элемента
b - фактическая ширина сечения элемента;
k cr - коэффициент, учитывающий снижение сопротивления сечения сдвигу
из-за возможного образования поверхностных трещин в опорных сечениях:
0,67 — для балок, прогонов из пиломатериала (брусья) и клееной древесины;
1,0 — других материалов на основе древесины
расчетное значение прочности древесины при сдвиге (скалывании) вдоль волокон
kmod ksys
при изгибе элемента
f v.d
m
f v.k

11. КОСОЙ ИЗГИБ

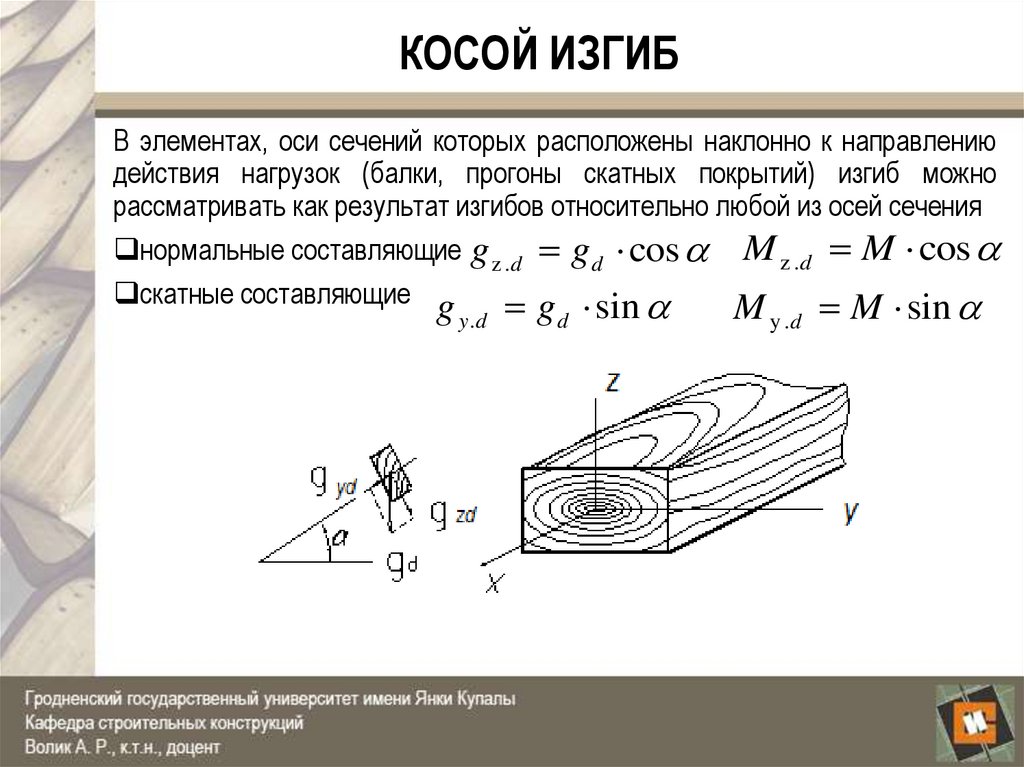
В элементах, оси сечений которых расположены наклонно к направлению
действия нагрузок (балки, прогоны скатных покрытий) изгиб можно
рассматривать как результат изгибов относительно любой из осей сечения
нормальные составляющие g z .d g d cos M z .d M cos
скатные составляющие g
g sin
y .d
d
M y .d M sin

12. КОСОЙ ИЗГИБ

Проверка несущей способности косоизгибаемых элементов
M y ,Ed
M z,Ed
M y ,Ed M z,Ed
km
1
km
1
M y ,R d
M z, R d
M y , R d M z, R d
VEd VRd
km - коэффициент, учитывающий распределение нормальных
напряжений по высоте поперечного сечения в зависимости от
его формы:
0,7 — для элементов прямоугольного поперечного сечения из цельной,
многослойной клееной древесины и LVL;
1,0 — для других поперечных сечений;
Предельное состояние эксплуатационной
косоизгибаемых элементов
2
пригодности
u uz u 2y

13. ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ДЕФОРМИРОВАНИЯ ПРИ ИЗГИБЕ

;
ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ
ДЕФОРМИРОВАНИЯ ПРИ ИЗГИБЕ
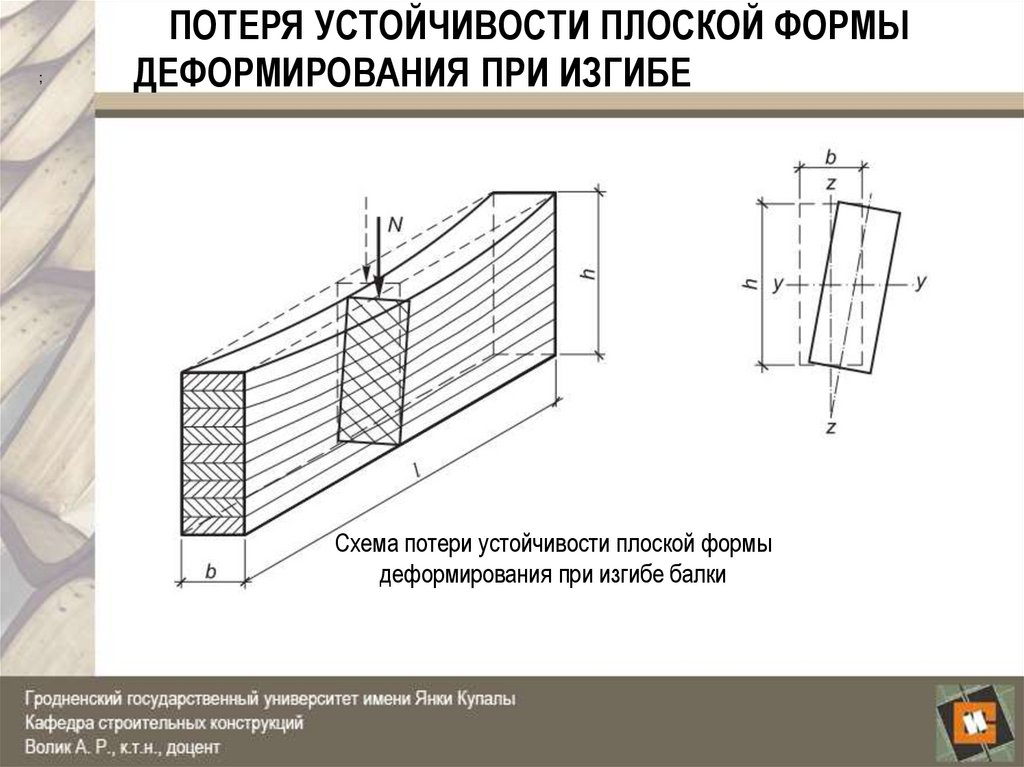
Схема потери устойчивости плоской формы
деформирования при изгибе балки

14. ПРОВЕРКА НА УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ДЕФОРМИРОВАНИЯ

;
ПРОВЕРКА НА УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ
ДЕФОРМИРОВАНИЯ
λrel,m > 0,75
M y ,Ed kcrit M y ,R d
My,Ed — расчетное значение изгибающего момента относительно оси у,
действующего в сечении элемента, обусловленное внешними
воздействиями;
kcrit — коэффициент, учитывающий уменьшение сопротивления в сечении
элемента из-за потери устойчивости плоской формы деформирования
(выпучивания);
My,Rd — максимальное расчетное значение сопротивления изгибу
относительно оси у в нормальном сечении элемента на рассматриваемом
участке l ef ; определяют по формуле
y ,R d
m,y ,d y ,br
M
f
W
fm,y,,d — расчетное значение прочности древесины при изгибе элемента
относительно оси у;
Wy,br — максимальный момент сопротивления брутто относительно оси у на
рассматриваемом участке lef.

15. kcrit — коэффициент, учитывающий уменьшение сопротивления в сечении элемента из-за потери устойчивости плоской формы

kcrit — коэффициент, учитывающий уменьшение сопротивления в сечении элемента изза потери устойчивости плоской формы деформирования (выпучивания)
приведенная гибкость изгибаемого элемента λrel,m
f m.k
rel.d
m.crit
σm,crit — критическое напряжение при изгибе элемента,
соответствующее его потере устойчивости

16. σm,crit — критическое напряжение изгиба

m,crit
M y ,crit
Wy
E0.05 I zG0.05 I tor
lef Wy
My,crit — упругий критический момент (зависит от вида нагрузки, прилагаемой к
изгибаемому элементу, его длины и условий закрепления, места приложения
нагрузки на элемент относительно его центра тяжести, модуля сдвига и
модуля упругости материала элемента, а также размеров поперечного
сечения)
Wy — момент сопротивления поперечного сечения относительно оси у - у;
E0,05, G0,05 — 5 %-ный квантиль модуля упругости, модуля сдвига древесины
древесины вдоль волокон (таблицы 6.2–6.4 СП);
Iz — момент инерции сечения относительно оси z;
Itor — крутящий момент инерции;
lef — эффективная (расчетная) длина элемента (балки), зависящая от
граничных условий элемента; принимают по таблице 7.1 СП.

17. ЭФФЕКТИВНАЯ ДЛИНА ЭЛЕМЕНТОВ (СП 5.05.01-2021)

18. σm,crit — критическое напряжение изгиба

При расчете изгибаемых элементов (балок) сплошного
прямоугольного сечения
из мягких пород древесины
m,crit
2
0,78b
E0.05
hlef
из твердых пород древесины,
клееной древесины
m,crit
M y ,crit
Wy
b2
b
E0.05G0.05 (1 0.63 )
hlef
h
E0,05 — 5 %-ный квантиль модуля упругости вдоль волокон;
Iz — момент инерции поперечного сечения относительно оси z - z;
G0,05 — 5 %-ный квантиль модуля сдвига вдоль волокон;
lef — эффективная (приведенная) длина пролета изгибаемого элемента,
зависящая от условий опирания и вида нагрузки;

19. σm,crit — критическое напряжение изгиба

Для уменьшения приведенной гибкости, т. е. повышения
поперечной устойчивости изгибаемого элемента (балки)
следует применять поперечное раскрепление в точках по
его длине. В этом случае за приведенную длину следует
принимать расстояние между соседними точками
раскрепления.
Если изгибаемый элемент в сжатой зоне раскреплен в
поперечном направлении по всей длине и на опорах выполнено
раскрепление по всей высоте сечения (например, сплошная
деревянная распорка), то коэффициент kcrit =1.

20. Расчет изгибаемых элементов по предельным состояниям эксплуатационной пригодности

uEd uСd
uEd — расчетное значение прогиба элемента в условиях предельного состояния
эксплуатационной пригодности, определяемое на основе расчета;
uСd — предельно допустимое значение прогиба элемента; принимают по таблице 8.1
СП.
Предельные значения прогибов

21. Расчет изгибаемых элементов по предельным состояниям эксплуатационной пригодности

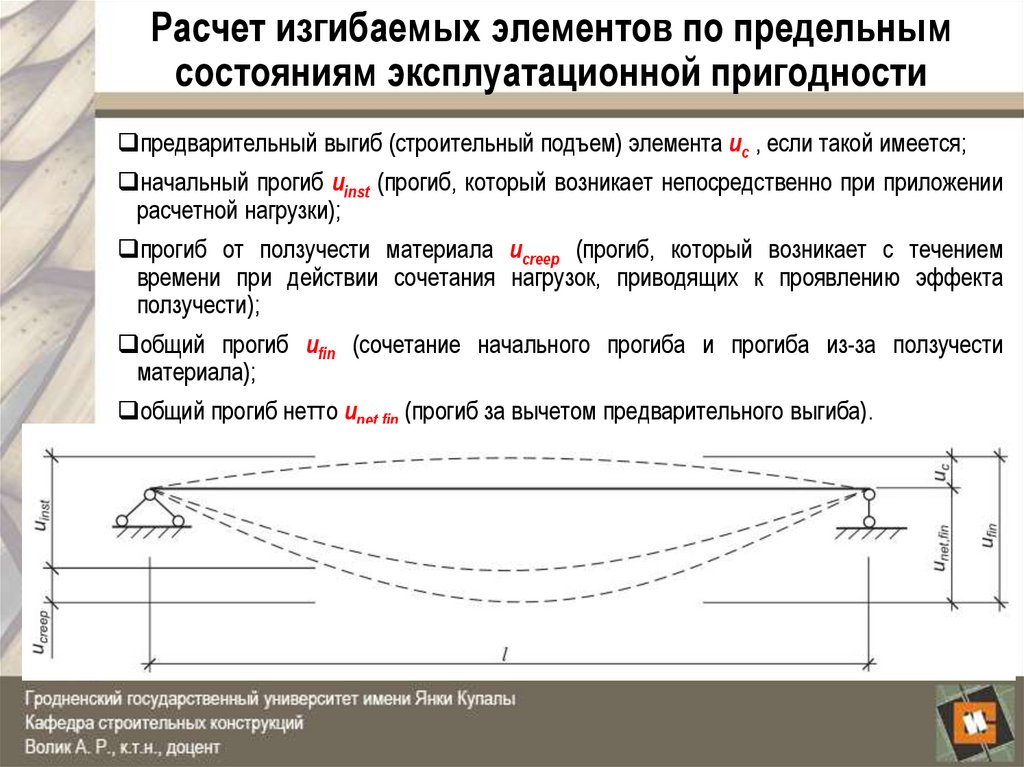
предварительный выгиб (строительный подъем) элемента uc , если такой имеется;
начальный прогиб uinst (прогиб, который возникает непосредственно при приложении
расчетной нагрузки);
прогиб от ползучести материала ucreep (прогиб, который возникает с течением
времени при действии сочетания нагрузок, приводящих к проявлению эффекта
ползучести);
общий прогиб ufin (сочетание начального прогиба и прогиба из-за ползучести
материала);
общий прогиб нетто unet,fin (прогиб за вычетом предварительного выгиба).

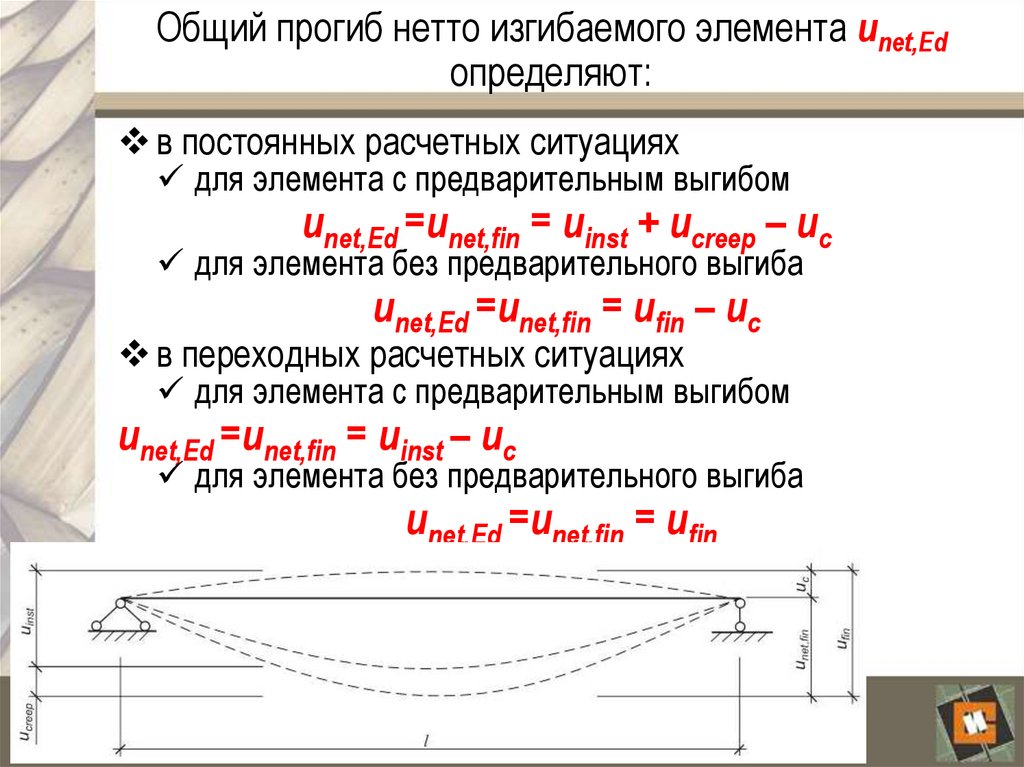
22. Общий прогиб нетто изгибаемого элемента unet,Ed определяют:

в постоянных расчетных ситуациях
для элемента с предварительным выгибом
unet,Ed =unet,fin = uinst + ucreep – uc
для элемента без предварительного выгиба
unet,Ed =unet,fin = ufin – uc
в переходных расчетных ситуациях
для элемента с предварительным выгибом
unet,Ed =unet,fin = uinst – uc
для элемента без предварительного выгиба
unet,Ed =unet,fin = ufin

23. НАЧАЛЬНЫЙ ПРОГИБ uinst

необходимо рассчитывать с использованием
характеристического сочетания воздействий,
соответствующего среднему значению модуля
упругости вдоль волокон E0,mean
и/или среднего значения модуля сдвига Gmean.
для деревянных элементов
Gmean
E0,mean
16
для элементов, изготовленных из материалов на основе древесины,
значения Gmean и E0,mean следует определять по данным на эти
материалы

24. Начальный прогиб u inst для дощатоклееных балок прямоугольного сечения и балок двутаврового сечения

u0
hmax 2 E0 mean
uinst
1 kv (
)
kh1
l
G0 mean
u0 — начальный прогиб балки без учета влияния переменности
высоты сечения и деформаций сдвига,
определяют в зависимости от типа балки, схемы опирания
и закона распределения нагрузки по длине рассчитываемого
элемента; расчетные схемы балок и формулы определения
начального прогиба принимают по таблице 8.2 СП;

25. Расчетные схемы балок, формулы для определения начального прогиба без учета влияния переменности высоты сечения и деформаций

сдвига u0

26. Начальный прогиб u inst

u0
hmax 2 E0 mean
uinst
1 kv (
)
kh1
l
G0 mean
hmax — максимальное значение высоты сечения балки;
l — пролет балки;
E0mean — среднее значение модуля упругости древесины вдоль
волокон для дощатоклееных и клеефанерных балок;
G 0mean — среднее значение модуля сдвига древесины для
дощатоклееных балок; для двутавровых балок принимают
модуль Gw,mean сдвига материала стенки (фанеры).

27. Начальный прогиб u inst

uinst
u0
h
E
1 kv ( max ) 2 0 mean
kh1
l
G0 mean
kh
—
коэффициент,
учитывающий
переменность
высоты поперечного сечения;
принимают по таблице 8.3 СП;
kv
—
коэффициент,
учитывающий
влияние
деформаций
сдвига
от
поперечной силы; принимают по
таблице 8.3 СП;
— отношение площади
сечения поясов к площади сечения
стенки.
Значения и рассчитывают
по формулам: = x / l, = h0 / hmax.

28. Определение начального прогиба плит с обшивками из фанеры, нагруженных равномерно-распределенной нагрузкой u inst

5 (g k qk )ld4
uinst
384 Ew,mean I ef kb
qk+qk — характеристическое значение погонной нагрузки;
ld — расчетное значение пролета плиты;
Ew,mean — среднее значение модуля упругости фанеры
обшивок;
Jef — приведенный момент инерции сечения плиты;
kb
—
редукционный
коэффициент,
учитывающий
уменьшенную ширину плиты по отношению к расчетному ее
значению; принимают равным 0,7.