Мехатронная система дозирования и смешения технологических компонентов в производстве древесноволокнистых плит

1.

Мехатронная система дозирования
и смешения технологических
компонентов в производстве
древесноволокнистых плит
Студент:
Амрани Юсеф
Руководитель:
Доцент, к.т.н., доцент Ваколюк Александр
Ярославич
Новочеркасск, 2025

2.

2
Цель работы
Целью бакалаврской работы является разработка мехатронной системы
дозирования и смешения компонентов. Для достижения поставленной цели
необходимо выполнить ряд задач: анализ технологического процесса в
первой главе, принятие ряда проектно-конструкторских решений во второй
главе, а также получение переходных характеристик исполнительного
устройства мехатронной системы в третьей главе работы.

3.

3
Технологическая часть
Технологический процесс производства ДВП включает ряд стадий:
1. Подготовка древесного сырья.
2. Дозирование и смешивание компонентов.
3. Формирование ковра.
4. Горячее прессование.
5. Термообработка и увлажнение.
6. Обрезка и шлифовка.
7. Контроль качества и упаковка.

4.

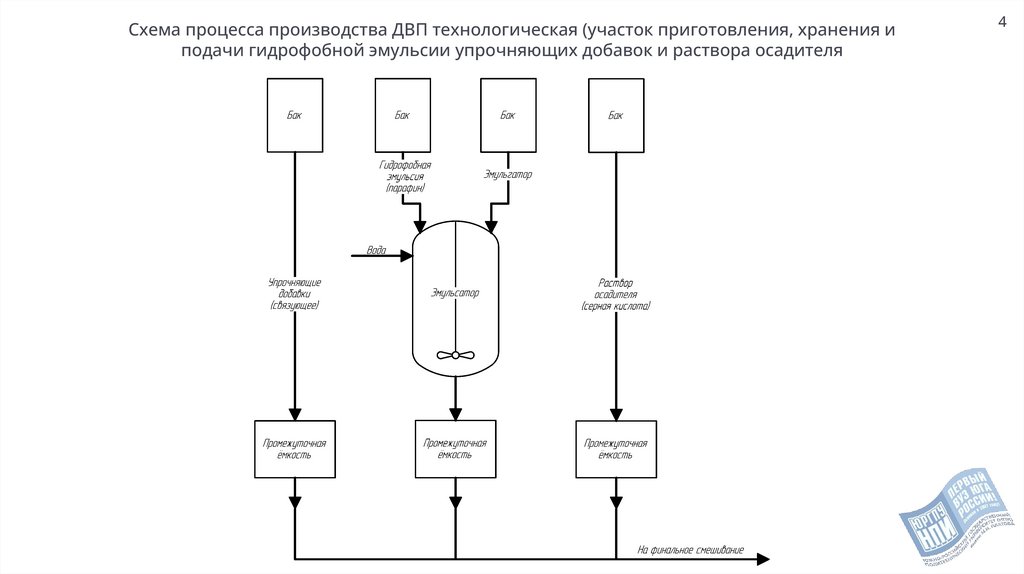
Схема процесса производства ДВП технологическая (участок приготовления, хранения и
подачи гидрофобной эмульсии упрочняющих добавок и раствора осадителя
4

5.

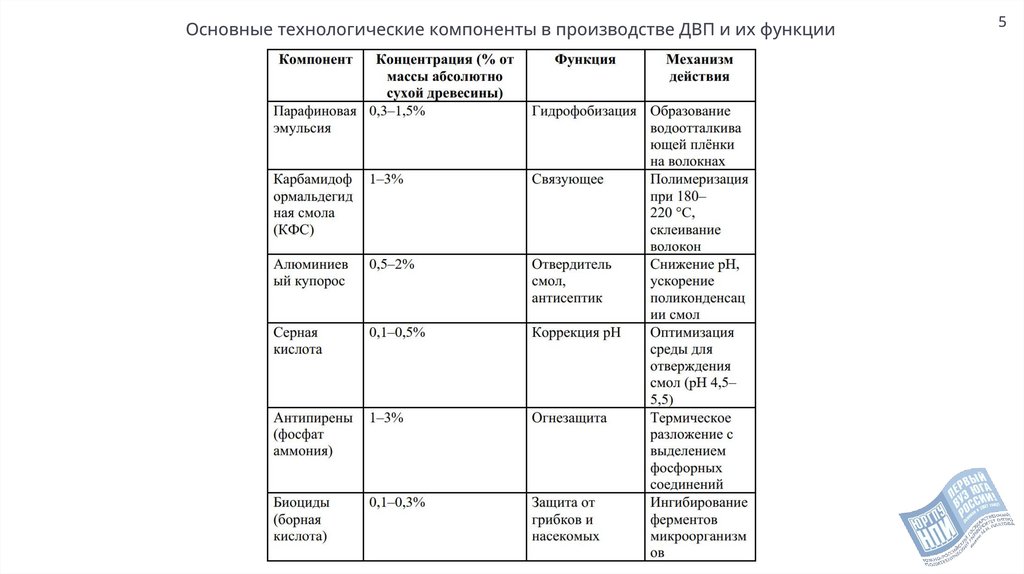
Основные технологические компоненты в производстве ДВП и их функции
5

6.

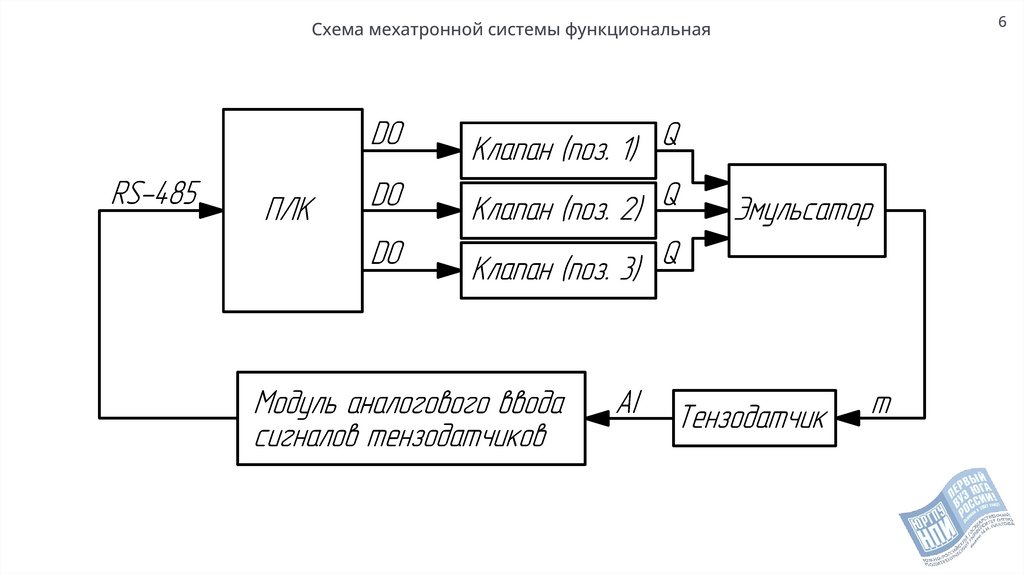
Схема мехатронной системы функциональная
6

7.

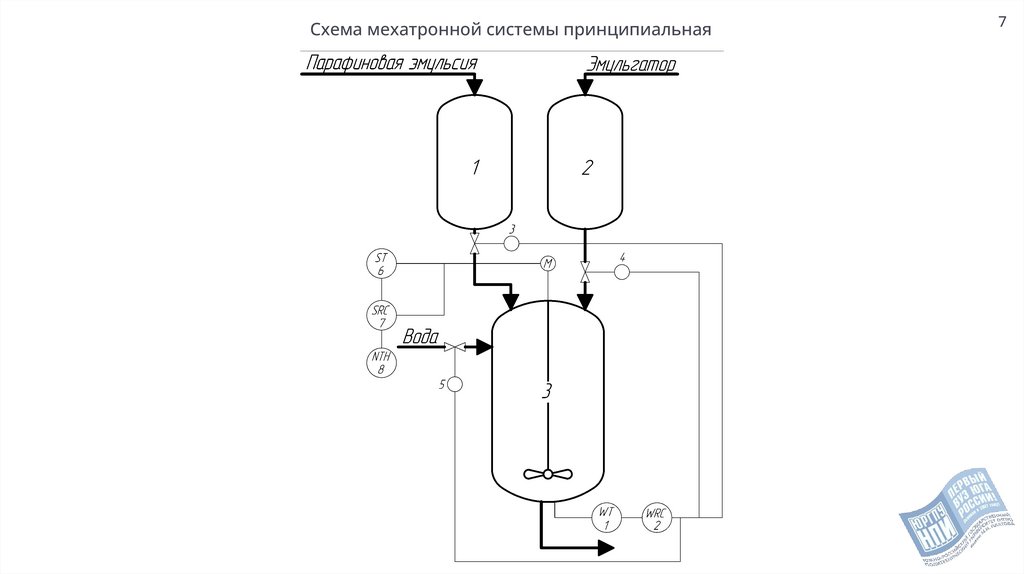
Схема мехатронной системы принципиальная
7

8.

Комплекс технических средств контроля и управления
Тахометр ТХ01-RS
Мотор-редуктор серии 7МЧ-М 50
Частотный преобразователь MEYERTEC VFD1
8

9.

Комплекс технических средств контроля и управления
Тензодатчик Т50
Электромагнитный клапан
DN.ru VS300-VT-NC-24VAC
Модуль аналогового ввода сигналов
тензодатчиков МВ110-224.1ТД
ОВЕН ПЛК200-01-CS
9

10.

10
Математическая модель электромагнитного клапана
Уравнение изменения силы тока обмотки катушки ЭМ клапана.
dI 1
(U RI ).
dt L
Система уравнений движения плунжера ЭМ клапана при открытии.
dv 1
(
F
mg
f
p
bv
cy
),
эм
зэ
пит
dt m
dy v.
dt
При этом функция перемещения плунжера должна вычисляться в соответствии с условием
vdt , если y 0,015,
y
0,015, если y 0,015.

11.

11
Математическая модель электромагнитного клапана
Уравнение расхода через клапан.
2
Q f кл ( y )
pпит pатм .
Ввиду того, что площадь проходного сечения клапана является функцией от положения плунжера,
примем линейной эту функциональную зависимость:
f кл kкл y b.

12.

12
Математическая модель электромагнитного клапана
Тогда, решив систему линейных алгебраических уравнений, можно найти неизвестные
коэффициенты:
f кл0 kкл y0 b,
f кл.max kкл ymax b.
Отсюда
f кл.max
kкл
.
ymax

13.

13
Математическая модель электромагнитного клапана
Итоговая система уравнений (при открытии).
Итоговая система уравнений (при закрытии).
dI 1
(
U
RI
),
dt L
dv 1 ( F mg f p bv cy ),
эм
зэ пит
dt m
dy
v,
dt
f кл kкл y,
Q f ( y ) 2 p p .
кл
пит
атм
dI 1
(
U
RI
),
dt L
dv 1 ( F mg f p bv cy ),
эм
зэ пит
dt m
dy
v,
dt
f кл kкл y,
Q f ( y ) 2 p p .
кл
пит
атм

14.

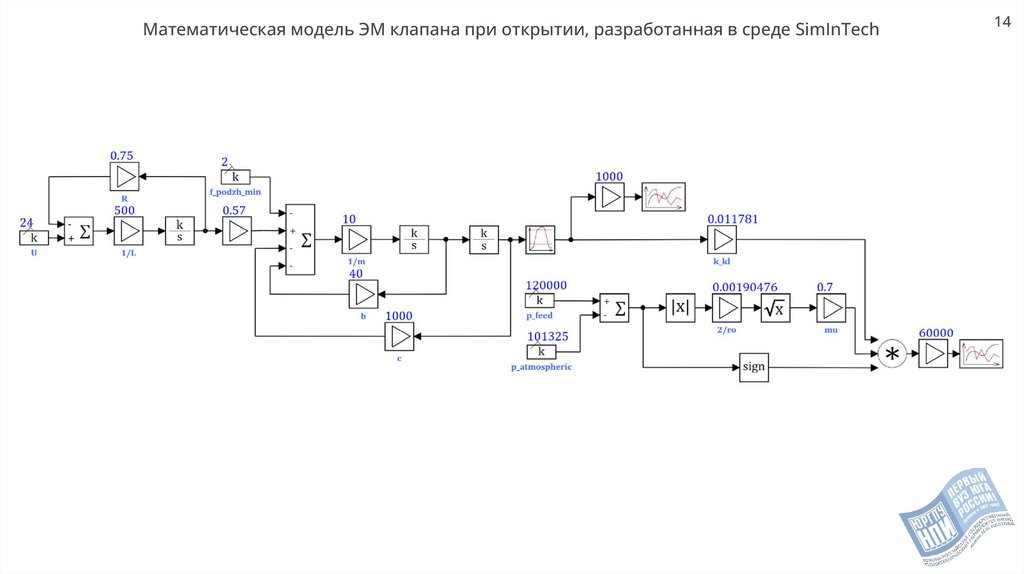
Математическая модель ЭМ клапана при открытии, разработанная в среде SimInTech
14

15.

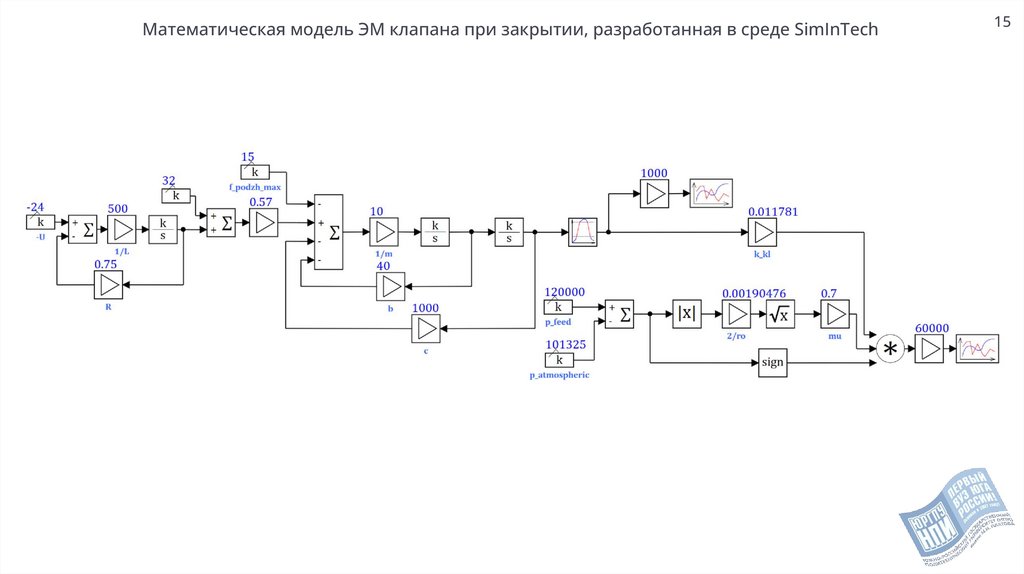
Математическая модель ЭМ клапана при закрытии, разработанная в среде SimInTech
15

16.

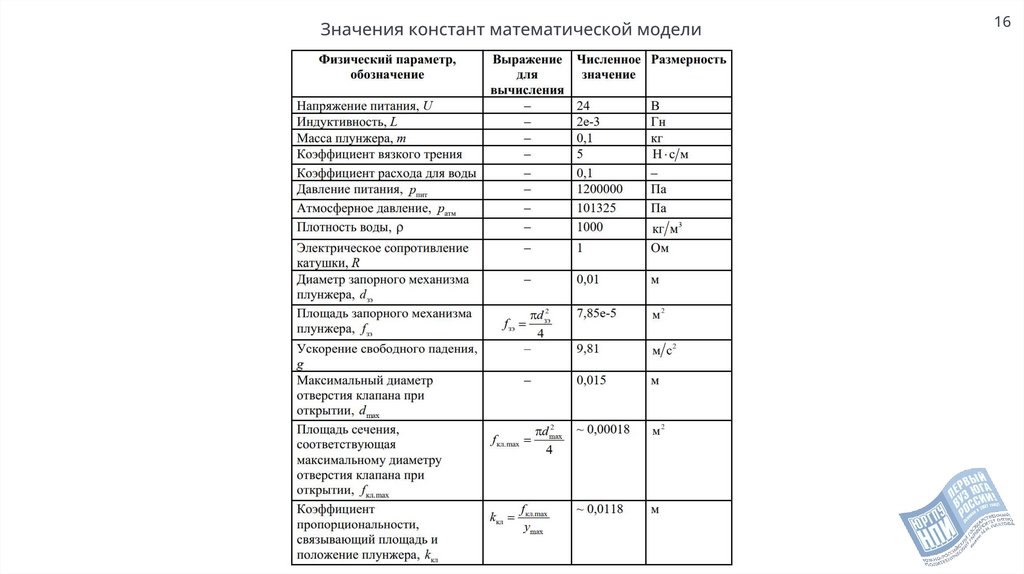
Значения констант математической модели
16

17.

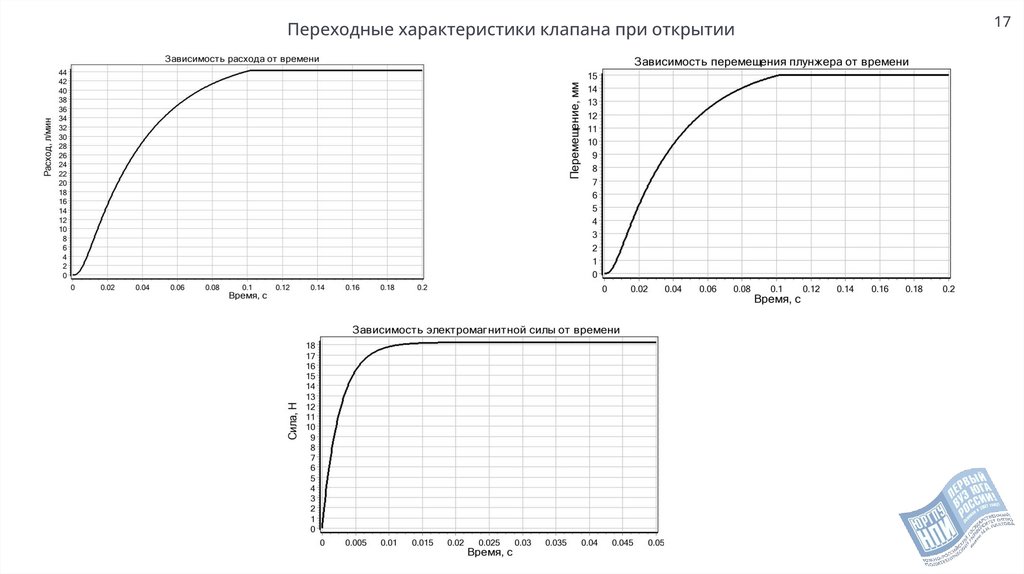
Переходные характеристики клапана при открытии
17

18.

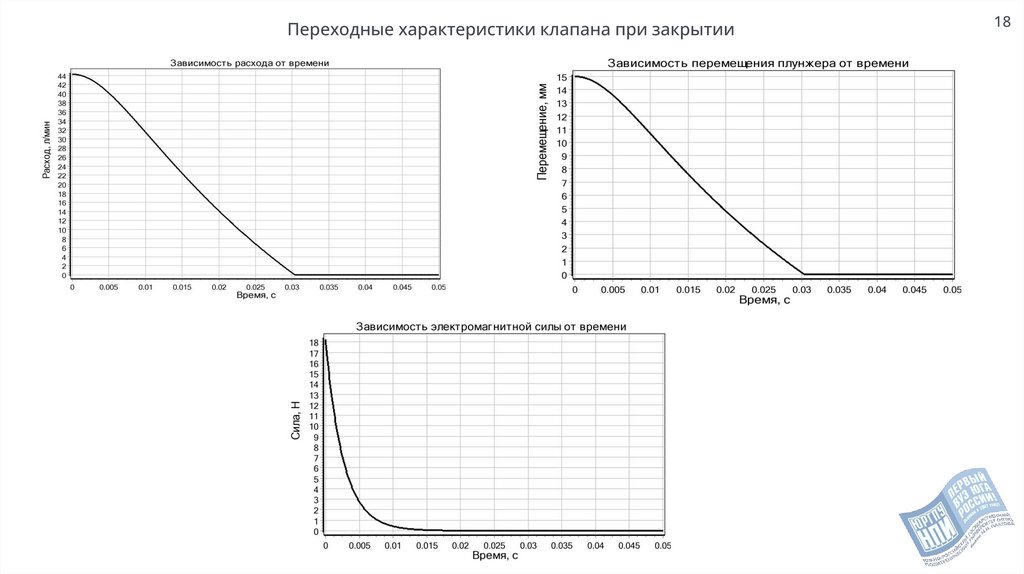
Переходные характеристики клапана при закрытии
18

19.

Благодарю за внимание
ЮРГПУ (НПИ) имени М. И. Платова,
346428, Ростовская обл.,
г. Новочеркасск, ул. Просвещения, 132
Амрани Юсеф
Новочеркасск, 2025